3.1直线的倾斜角与斜率 课件(共27张PPT)---2020-2021学年高一下学期数学人教版必修2
文档属性
| 名称 | 3.1直线的倾斜角与斜率 课件(共27张PPT)---2020-2021学年高一下学期数学人教版必修2 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 23:01:47 | ||
图片预览






文档简介
第三章
直线与方程
几何问题的研究——主要通过两种不同的方式
1、直接依据几何图形中的点、线、面的关系研究几何图形的性质。例如前面一、二章的学习就是如此;
2、就是用代数的方法来研究几何图形的性质。即借助直角坐标系,通过坐标的运算来研究图形的几何性质,这就是本章将开始学习的————“解析几何”基本的思想方法。
3.1直线的倾斜角与斜率
观察下列的翘翘板,翘翘板的位置固定吗?
思考--
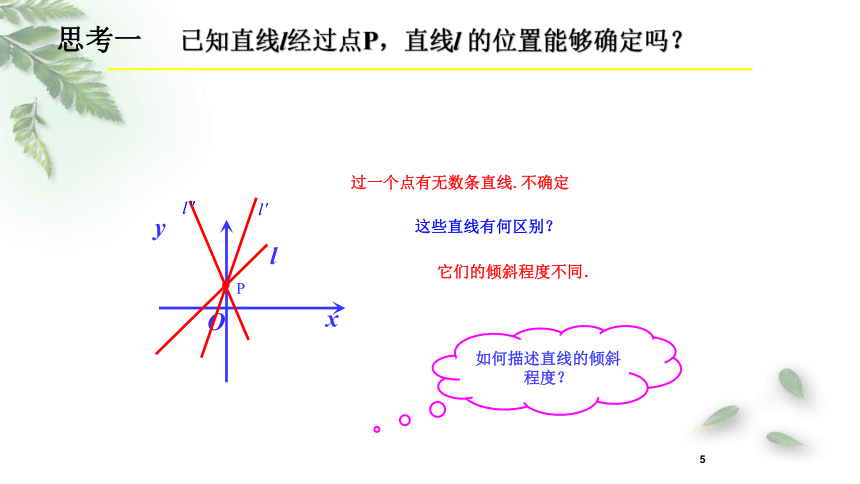
思考一 已知直线l经过点P,直线l 的位置能够确定吗?
y
x
O
l
P
过一个点有无数条直线.不确定
这些直线有何区别?
它们的倾斜程度不同.
如何描述直线的倾斜程度?
新知识一
直线倾斜角—定义
当直线与x轴相交时,我们取x轴为基准,x轴正向与直线l向上方向所成的角α叫做直线l的倾斜角。
特别地,1 当直线l与x轴平行或重合时,规定α=0°.
注意: (1)直线向上方向;
(2)x轴的正方向。
2.当直线与x轴垂直时,
下列图中,表示直线的倾斜角的是( )
找一找
C
A
B
C
D
新知识一
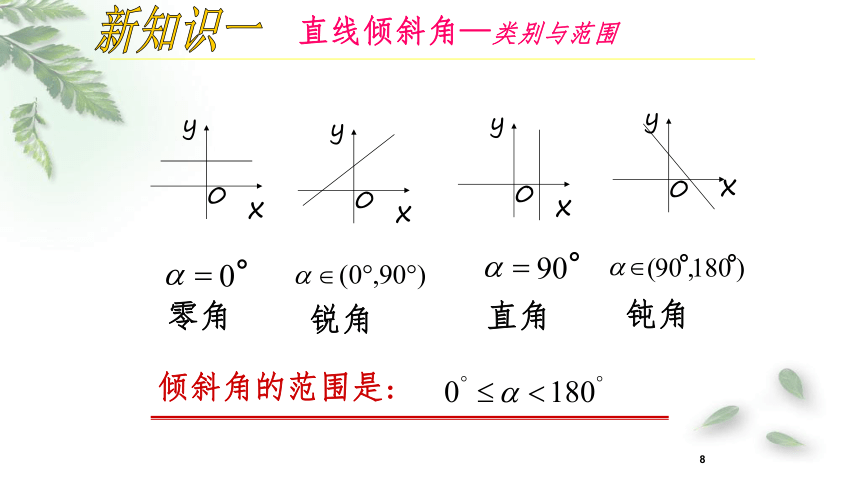
倾斜角的范围是:
直线倾斜角—类别与范围
x
y
0
零角
°
=
0
a
x
y
0
直角
°
=
90
a
x
y
0
钝角
)
180
,
90
(
°
°
?
a
x
y
0
锐角
思考--
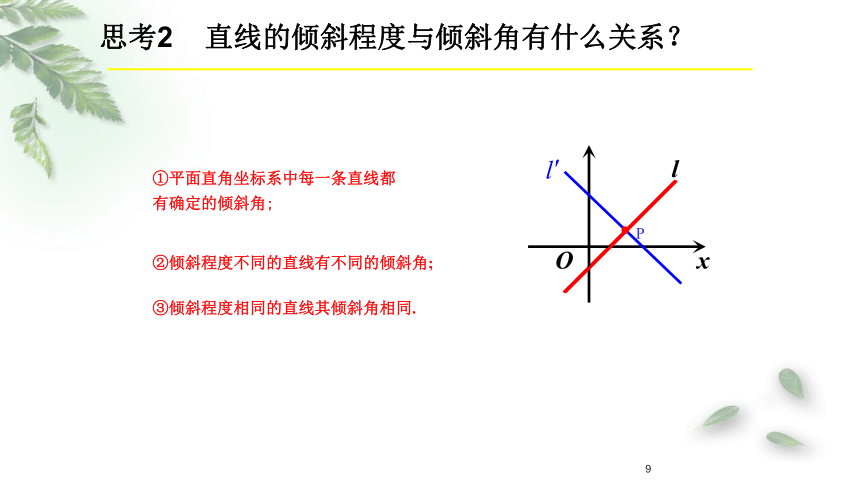
思考2 直线的倾斜程度与倾斜角有什么关系?
①平面直角坐标系中每一条直线都
有确定的倾斜角;
②倾斜程度不同的直线有不同的倾斜角;
③倾斜程度相同的直线其倾斜角相同.
x
O
l
P
9
思考--
思考3 确定平面直角坐标系中一条直线的几何要素是什么?
x
y
o
α
直线上的一个定点及它的倾斜角
二者缺一不可.
思考四 日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
坡度越大,坡就越陡.
前进量
升
高
量
α
“坡度比”是“倾斜角”的正切值.
x
y
o
tanα
例如:
新知识二
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率(slope)。
用小写字母 k 表示,即:
直线斜率的概念
x
y
o
新知识二
---直线斜率的概念
如右图所示,当直线与x 轴垂直(即倾斜角 )时,直线的斜率是多少?
综上所述:斜率与倾斜角的关系
为
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
0°< < 90°
= 90°
90°< <180°
= 0°
k=0
k >0
k不存在
k<0
请观察下列语句:
A 、任一条直线都有倾斜角,也都有斜率
B、任一条直线都有倾斜角,但不一定有斜率
C 、任一条直线都有斜率,但不一定有倾斜角
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
B、E
其中正确的语句有_________
辨一辨
思考五
P1(x1,y1)
P2(x2,y2)
x
y
O
α
P2(x2,y2)
P1(x1,y1)
O
x
y
α
已知直线上两点坐标:P1(x1,y1)P2(x2,y2),(x1≠x2),如何求斜率k?
当α为锐角时
以往我们一般在怎样的图形中求一个角的正切值呢?
思考五
由两点确定的直线的斜率(锐角)
公式与点的顺序无关
思考五
由两点确定的直线的斜率(钝角)
当α为钝角时
当α为零角时
思考六
由两点确定的直线的斜率(零度)
成立
思考:当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
不成立,因为分母为0。
思考七
由两点确定的直线的斜率(直角)
直线的斜率公式:
综上所述,我们得到经过两点
的直线斜率公式:
新知识三
由两点确定的直线的斜率公式
例1 如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
y
直线AB与CA的倾斜角为锐角,直线BC的倾斜角为钝角.
新知识四
例题
例2
解:
1、直线 经过点( )和( ),其中 则( )
(C) 的斜率不存在 (D) 的倾斜角不存在
(A) 的倾斜角是 (B) 的倾斜角是
B
新知识巩固
--练习
2、如果过点P(-2,m)和Q(m,4)的直线的斜率等于1,那么m的值为( )
(A)1 (B)4
(C)1或3 (D)1或4
A
新知识巩固练习
3、已知不同两点A(a,2),B(3,b+1),且直线AB的倾斜角为90°,则a,b的值为( )
(A)a=3, b=1
(B)a=3, b=2
(C)a=2, b=3
(D)a=3, b∈R且b≠1
D
4、已知过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是 .
(-2,1)
课堂小结课堂小结
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
3、斜率k与倾斜角 之间的关系:
4、斜率公式:
直线与方程
几何问题的研究——主要通过两种不同的方式
1、直接依据几何图形中的点、线、面的关系研究几何图形的性质。例如前面一、二章的学习就是如此;
2、就是用代数的方法来研究几何图形的性质。即借助直角坐标系,通过坐标的运算来研究图形的几何性质,这就是本章将开始学习的————“解析几何”基本的思想方法。
3.1直线的倾斜角与斜率
观察下列的翘翘板,翘翘板的位置固定吗?
思考--
思考一 已知直线l经过点P,直线l 的位置能够确定吗?
y
x
O
l
P
过一个点有无数条直线.不确定
这些直线有何区别?
它们的倾斜程度不同.
如何描述直线的倾斜程度?
新知识一
直线倾斜角—定义
当直线与x轴相交时,我们取x轴为基准,x轴正向与直线l向上方向所成的角α叫做直线l的倾斜角。
特别地,1 当直线l与x轴平行或重合时,规定α=0°.
注意: (1)直线向上方向;
(2)x轴的正方向。
2.当直线与x轴垂直时,
下列图中,表示直线的倾斜角的是( )
找一找
C
A
B
C
D
新知识一
倾斜角的范围是:
直线倾斜角—类别与范围
x
y
0
零角
°
=
0
a
x
y
0
直角
°
=
90
a
x
y
0
钝角
)
180
,
90
(
°
°
?
a
x
y
0
锐角
思考--
思考2 直线的倾斜程度与倾斜角有什么关系?
①平面直角坐标系中每一条直线都
有确定的倾斜角;
②倾斜程度不同的直线有不同的倾斜角;
③倾斜程度相同的直线其倾斜角相同.
x
O
l
P
9
思考--
思考3 确定平面直角坐标系中一条直线的几何要素是什么?
x
y
o
α
直线上的一个定点及它的倾斜角
二者缺一不可.
思考四 日常生活中,还有没有表示倾斜程度的量?
前进量
升
高
量
坡度越大,坡就越陡.
前进量
升
高
量
α
“坡度比”是“倾斜角”的正切值.
x
y
o
tanα
例如:
新知识二
我们把一条直线的倾斜角 的正切值叫做这条直线的斜率(slope)。
用小写字母 k 表示,即:
直线斜率的概念
x
y
o
新知识二
---直线斜率的概念
如右图所示,当直线与x 轴垂直(即倾斜角 )时,直线的斜率是多少?
综上所述:斜率与倾斜角的关系
为
p
o
y
x
y
p
o
x
p
o
y
x
p
o
y
x
0°< < 90°
= 90°
90°< <180°
= 0°
k=0
k >0
k不存在
k<0
请观察下列语句:
A 、任一条直线都有倾斜角,也都有斜率
B、任一条直线都有倾斜角,但不一定有斜率
C 、任一条直线都有斜率,但不一定有倾斜角
D 、两直线的倾斜角相等,它们的斜率也相等
E 、两直线的斜率相等,它们的倾斜角也相等
B、E
其中正确的语句有_________
辨一辨
思考五
P1(x1,y1)
P2(x2,y2)
x
y
O
α
P2(x2,y2)
P1(x1,y1)
O
x
y
α
已知直线上两点坐标:P1(x1,y1)P2(x2,y2),(x1≠x2),如何求斜率k?
当α为锐角时
以往我们一般在怎样的图形中求一个角的正切值呢?
思考五
由两点确定的直线的斜率(锐角)
公式与点的顺序无关
思考五
由两点确定的直线的斜率(钝角)
当α为钝角时
当α为零角时
思考六
由两点确定的直线的斜率(零度)
成立
思考:当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?
不成立,因为分母为0。
思考七
由两点确定的直线的斜率(直角)
直线的斜率公式:
综上所述,我们得到经过两点
的直线斜率公式:
新知识三
由两点确定的直线的斜率公式
例1 如下图,已知A(3,2),B(-4,1),C(0,-1),求直线AB,BC,CA的斜率,并判断这些直线的倾斜角是锐角还是钝角。
x
o
.
.
.
.
.
.
.
.
.
.
A
B
C
y
直线AB与CA的倾斜角为锐角,直线BC的倾斜角为钝角.
新知识四
例题
例2
解:
1、直线 经过点( )和( ),其中 则( )
(C) 的斜率不存在 (D) 的倾斜角不存在
(A) 的倾斜角是 (B) 的倾斜角是
B
新知识巩固
--练习
2、如果过点P(-2,m)和Q(m,4)的直线的斜率等于1,那么m的值为( )
(A)1 (B)4
(C)1或3 (D)1或4
A
新知识巩固练习
3、已知不同两点A(a,2),B(3,b+1),且直线AB的倾斜角为90°,则a,b的值为( )
(A)a=3, b=1
(B)a=3, b=2
(C)a=2, b=3
(D)a=3, b∈R且b≠1
D
4、已知过点P(1-a,1+a)和Q(3,2a)的直线的倾斜角为钝角,则实数a的取值范围是 .
(-2,1)
课堂小结课堂小结
1、直线的倾斜角定义及其范围:
2、直线的斜率定义:
3、斜率k与倾斜角 之间的关系:
4、斜率公式:
