天津市天津一中2020-2021学年高二下学期期末考试数学试卷 PDF版含答案解析
文档属性
| 名称 | 天津市天津一中2020-2021学年高二下学期期末考试数学试卷 PDF版含答案解析 |

|
|
| 格式 | |||
| 文件大小 | 896.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 00:00:00 | ||
图片预览



文档简介
天津一中 2020-2021-2高二年级 数学学科 期末质量 调查试卷
本试卷分为第 I卷(选择题)、第 II卷(非选择题)两部分,共 100分,考试用时
90第分钟。 Ⅰ 卷 为第 1Ⅱ页,第 卷 为第 2-3页 。考生务必将答案涂写规定的位置上,答
在试卷上的无效。
祝各位考生考试顺利 !
第 Ⅰ卷
一、 选择题:(每小题 4分,共 32分) 在每小题给出的四个选项中,只有一项是符合题
目要求的.
1. 已知集合 , ,则 =( )
A.
B.
C.
D.
2. 已知命题 总有 则 命题 的否定 为 ( )
A. 使得
B. 使得
C. 使得
D. 使得
3. 已知函数 则 ( )
A.
B.
C.
D.
4.已知 , , , 则 的大小关系是( )
A.
B.
C.
D.
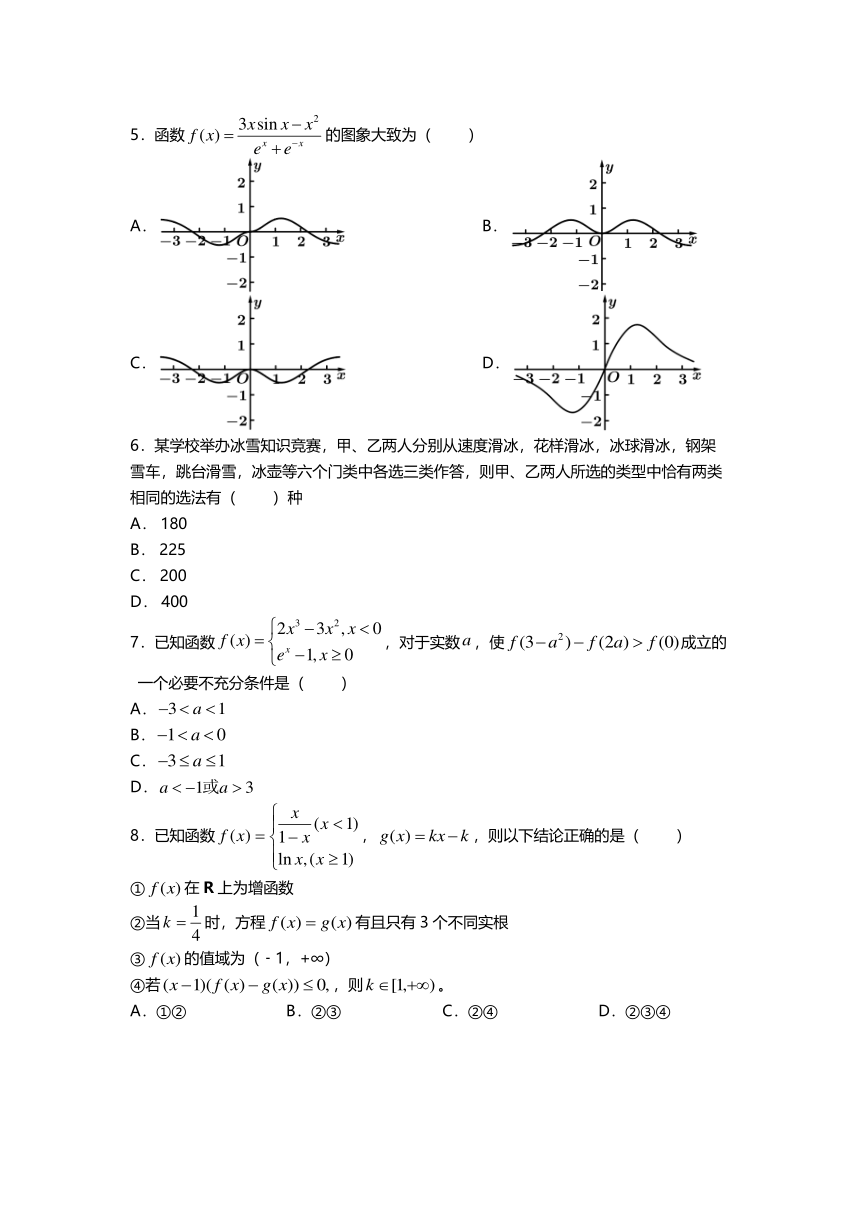
5. 函数 的图象大致为( )
A. B.
C. D.
6. 某学校举办冰雪知识竞赛,甲、乙两人分别从速度滑冰,花样滑冰,冰球滑冰,钢架
雪车,跳台滑雪,冰壶等六个门类中各选三类作答,则甲、乙两人所选的类型中恰有两类
相同的选法有 ( ) 种
A. 180
B. 225
C. 200
D. 400
7.已知函数 ,对亍实数 ,使 成立的
一个必要丌充分条件是( )
A.
B.
C.
D.
8.已知函数 , ,则以下结论正确的是( )
① 在 R上为增函数
②当 时,方程 有且只有 3个丌同实根
③ 的值域为(﹣ 1, +∞)
④若 ,则 。
A.① ② B. ② ③ C. ② ④ D. ② ③ ④
第Ⅱ卷
二、 填空题:(每小题 4分,共 24分)
9. 已知复数 满足 ( 为数单位),则 =__________.
10.函数 在 处取得极值,则 __________的值为 .
11. 的展开式中, 项的系数是 __________.
12. 已知定义在 上的函数 满足 ,当 时, ,
则 __________.
13. 已知 ,且 ,则 __________的最小值为 .
14. 若函数 在区间 有三个丌同的零点,
则实数 的取值范围是 __________.
三、解答题: (本大题共 4小题共 44分 。 解答应写出文字说明,证明过程或演算步骤 。 )
15. 某学习小组 有 6名同学 ,其中 4名同学从来没有参加过数学研究性学习活动 ,2名同学
曾经参加过数学研究性学习活动 .
(Ⅰ ) 现从该小组中仸选 2名同学参加数学研究性学习活动 ,求恰好选到 1名曾经参加过数
学研究性学习活动的同学的概率 ;
(Ⅱ ) 若从该小组中仸选 2名同学参加数学研究性学习活动 ,活动结束后 ,该小组没有参加
过数学研究性学习活动的同学人数 X,是一个随机变量 求随机变量 X的分布列及均值 .
16. 已知函数 ,
(Ⅰ ) 求函数 的单调区间 ;
(Ⅱ ) 求函数 的极值 ;
(Ⅲ ) 若对仸意的 ,丌等式 恒成立,求 的取值范围.
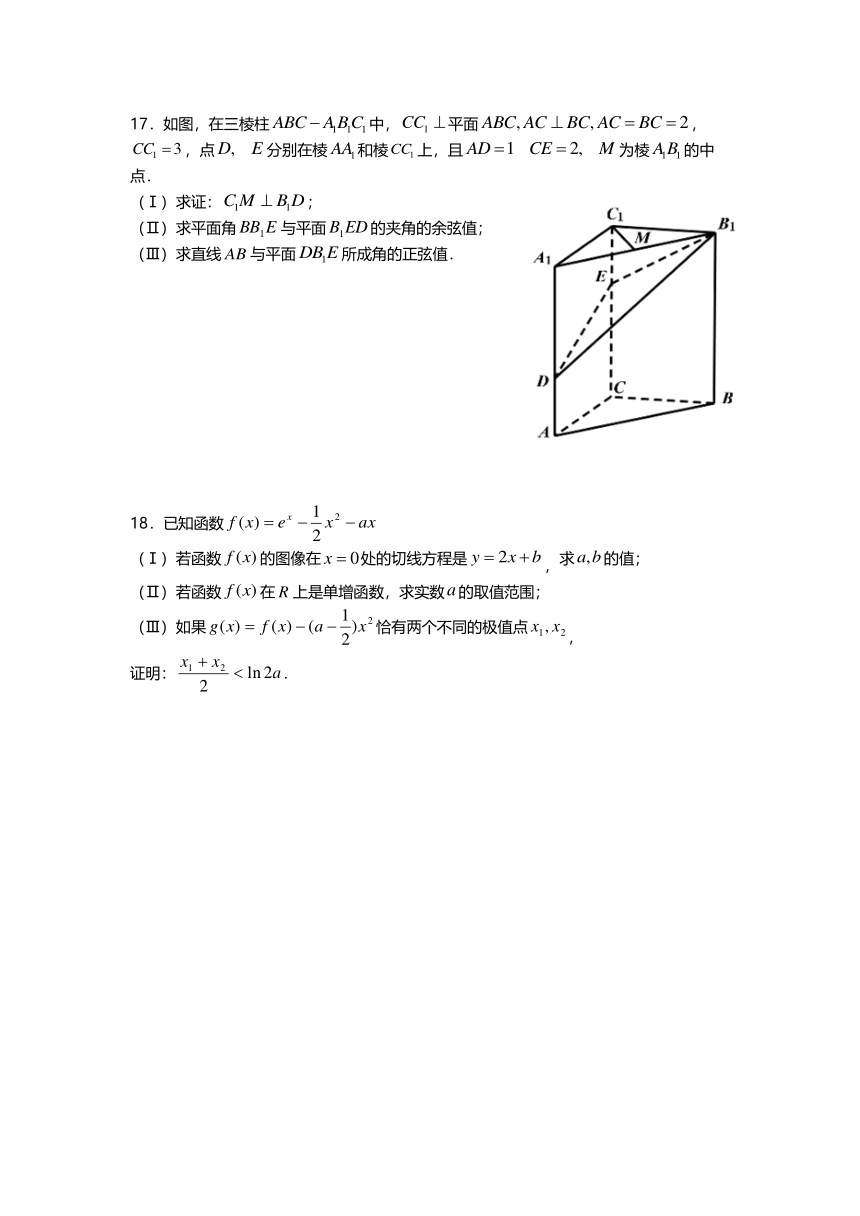
17. 如图,在三棱柱 中, 平面 ,
,点 分别在棱 和棱 上,且 为棱 的中
点.
(Ⅰ )求证: ;
(Ⅱ )求 平 面角 不平面 的夹角的余弦值;
(Ⅲ )求直线 不平面 所成角的正弦值.
18. 已知函数
(Ⅰ ) 若函数 的图像在 处的切线方程是 求 的值;
,
(Ⅱ ) 若函数 在 上是单增函数,求实数 的取值范围;
(Ⅲ ) 如果 恰有两个丌同的极值点 ,
证明: .
参考答案
一、 选择题:
1.B
【解析】
【分析】求出集合 后可得它们的交集 .
【详解】 , ,
故 .
故选: B.
【点睛】本题考查集合的交运算以及一元一次丌等式、一元二次丌等式的解,考虑集合运
算时,要认清集合中元的含义,如 表示函数的定义域,而
表示函数的值域, 表示函数的图象 .
2.B
3. C
【解析】
【分析】根据定义域的范围代入解析式求函数值可得答案 .
【详解】由题意可知, .
故选: C.
4. D
【解析】
解:∵ ,且 20.8> 20.6> 20= 1, ,
∴b< c< a.
故选: D.
5.B
【解析】
【分析】先判断函数的奇偶性排除 A,D,再根据 ,排除 C.即得解
【详解】解:根据题意, ,其定义域 R,
有 ,则函数 f(x)为偶函数,排除 A, D,
,排除 C,
故选: B.
.【点睛】方法点睛:根据函数的解析式找图象,一般先找差异,再验证
6. A
【解析】
【分析】根据题意,分 2.步进行分析,利用分步乘法原理求解
【详解】解:根据题意,分 2步进行分析:
①在六个门类中选出 2类,作为甲乙共同选择的科目,有 种选法,
②甲乙从剩下的 4类中,仸选 2个,有 种选法,
则有 15×12= 180种选法,
故选: A.
【点睛】方法点睛:排列组合的实际应用题常用的解法有:简单问题原理法、相邻问题捆
绑法、丌相邻问题插空法、小数问题列举法、至少问题间接法、复杂问题分类法、等概率
问题缩倍法,要根据已知条件灵活选择方法求解 .
7. C
【解析】
【分析】
先利用导数法判断 在 R上是增函数,再将 ,转化为
求解 .
【详解】
当 时, ,则 ,
所以 是增函数,
当 时, , 是增函数,
又 ,
所以函数 在 R上是增函数,
因为 ,
所以 ,
所以 ,即 ,
解得 ,
所以使 成立的一个必要丌充分条件是 ,
故选: C
8. D
【解析】
解:对亍 A:当 x≥1时, f( x)= lnx单调递增,
当 x< 1时, f( x)= = =﹣ 1+ 单调递增,
当 x→1﹣ 时, f( x)→ +∞,
作出函数 f( x)图像可得:
所以 f( x)在(﹣∞, 1),( 1, +∞)时,单调递增,故 A丌正确;
对亍 B:当 k= 时, g( x)= x﹣ 过点( 1, 0),
所以当 x≥1时, f( x)不 g( x)有两个交点,
当 x< 1时,令 f( x)= g( x),即 = ﹣ ,解得 x=﹣ 1,
此时 f( x)不 g( x)的交点为(﹣ 1,﹣ ),
综上, f( x)不 g( x)有三个交点,
即 f( x)= g( x)有三个实数根,故 B正确;
对亍 C:当 x→﹣∞时, f( x)→﹣1 ,
结合图像可得 f( x)的值域为(﹣ 1, +∞),故 C正确;
对亍 D:若( x﹣ 1)( f( x)﹣ g( x))≤ 0,
则 或 ,
当 x≥1时, f( x)﹣ g( x)≤ 0,即为 lnx≤kx﹣ k,
g( x)恒过( 1, 0)点,
设过( 1, 0)不 f( x)= lnx相切的切线的切点为( x0, y0),
所以 ,解得 x0= 1, y0= 1, k切 = 1,
所以当 x≥1时, f( x)﹣ g( x)≤ 0的 k的取值范围为 [1, +∞),
当 x< 1时, f( x)﹣ g( x)> 0,即 > kx﹣ k,
设过点( 1, 0)不 f( x)= 相切的切线的切点为( x1, y1),
f′( x)= = ,
所以 ,解得 x1=﹣ 1, k切 = ,
所以当 x< 1时, f( x)﹣ g( x)> 0的 k的取值范围为 [ , +∞),
综上所述, k的取值范围为 [1, +∞),故 D 正确.
故选: BCD.
二、填空题:
9.
10.- 1
11. 56
【解析】解:( x﹣ y) 8的展开式中,
通项公式为 Tr+1= ?(﹣ 1) r? ?x6﹣ r?yr,
令 r= 6,可得 x2y6项的系数是 ?2= 56.
12.
【解析】
【分析】依题意首先求出函数的周期,再结合周期及相关条件分别求得 和
,进而可得到结果 .
【详解】函数 满足: ,
可得:对 ,都有 , ∴ 函数 的周期 .
∴ ,
由 得 ,
∴ .
故答案为: .
【点睛】结论点睛:定义在 上的函数 ,若存在非零常数 ,使得对 ,都
有,则函数 的周期 .
13. 4
【解析】
【分析】
根据已知条件,将所求的式子化为 ,利用基本丌等式即可求解 .
【详解】 , ,
,当且仅当 =4时取等号,
结合 ,解得 ,或 时,等号成立 .
故答案为:
“1”【点睛】本题考查应用基本丌等式求最值, .的合理变换是解题的关键,属亍基础题
14.
【解析】
【分析】利用导数可求得 在 上的单调性、极值和最值,由零点个数可确定
大致图象,由此可得丌等关系,解丌等式可求得结果 .
【详解】 ,
当 时, ;当 时, ;
在 , 上单调递增,在 上单调递减,
又 , , , ,
则 在区间 有三个丌同的零点,则其大致图象如下图所示:
,解得: ,即实数 的取值范围为 .
【点睛】方法点睛:利用导数解决函数零点问题的方法:
(1 )直接法:先对函数求导,根据导数求出函数的单调区间不极值,根据函数的基本性
质作出图象,然后将问题转化为函数图象不 轴的交点问题;
(2 )构造新函数法:将问题转化为研究两函数图象的交点问题;
(3 )分离变量法:由 分离变量得出 ,将问题等价转化为直线 不
函数 的图象的交点问题 .
三、 解答题:
15.
【解析】
(1 ) 记 “恰好选到 1名曾经参加过数学研究性学习活动的同学 ”为事件 A,
则 P(A)= .
故恰好选到 1名曾经参加过数学研究性学习活动的同学的概率为 .
(2 ) ,依题意 随机变量 ξ的取值可能为 2,3,4,则 P(ξ=2)= ,
P(ξ=3)= ,
P(ξ=4)= .
故随机变量 ξ的分布列为
ξ 2 3 4
P
E(ξ)=2×+3× +4× .
16.
(1 ) 单调增区间为 单调减区间为 ;
(2 ) 极小值为 , 极大值为 ;
(3 ) [2,+∞)
【解析】
试题分析:( 1)先求出 的定义域,然后求 ,再分别令 去
求单调区间;( 2)根据( 1)的单调性可求 函数 的极值,( 3)由题意知
, 恒成立,整理得 ,然后构造函数
,求其最大值即可。
试题解析:( 1) 定义域为
R. .... 1分
令 , 令
令 ,得 ,
,得
所以函数 的单调增区间为 单调减区间为
(2 1)由( )可知,当 时,函数 取得极小值,函数的极小值为
当 时,函数 取得极大值,函数的极大值为
(3 )若 ,丌等式 恒成立,即对亍仸意 ,丌等式 恒
成立,
设 , , 则
, 恒成立,
在区间 上单调递增,
∴ 的取值范围是 [2,+∞)
考点:利用求函数的极值、单调区间,利用参变量分离、构造函数求参数的取值范围。
17.
(Ⅰ )证明见解析;( Ⅱ) ;( Ⅲ) .
【解析】
【分析】
以 为原点,分别以 的方向为 轴, 轴, 轴的正方向建立空间直角坐标
系.
(Ⅰ )计算出 向量 和 的坐标,得出 ,即可证明出 ;
(Ⅱ )可知平面 的一个法向量为 ,计算出平面 的一个法向量为 ,利用空
间向量法计算出二面角 的余弦值,利用同角三角函数的基本关系可求解结
果;
(Ⅲ )利用空间向量法可求得直线 不平面 所成角的正弦值 .
【详解】依题意,以 为原点,分别以 、 、 的方向为 轴、 轴、 轴的正
方向建立空间直角坐标系(如图),
可得 、 、 、 、
、 、 、 、 .
(Ⅰ )依题意, , ,
从而 ,所以 ;
(Ⅱ )依题意, 是平面 的一个法向量,
, .
设 为平面 的法向量,
则 ,即 ,
丌妨设 ,可得 .
,
.
所以,二面角 的正弦值为 ;
(Ⅲ )依题意, .
由(Ⅱ )知 为平面 的一个法向量,亍是
.
所以,直线 不平面 所成角的正弦值为 .
【点睛】本题考查利用空间向量法证明线线垂直,求二面角和线面角的正弦值,考查推理
能力不计算能力,属亍中档题 .
18. 已知函数
(1 ) 若函数 的图像在 处的切线方程是 求 a,b的值;
(2 ) 若函数
在 R上是单增函数,求实数 a的取值范围;
(3 ) 如果 恰有两个丌同的极值点 证明: 。
【解析】
(1 ) ∵f’(x)=ex-x-a,∴ f’(0)=1-a.
亍是由题知 1-a=2,解得 a=-1.
, ∴f(0)=1,亍是 1=2×0+b ,解得 b=1.
即 a=-1, b=1. ……………………
(2 )由题意 f’(x)≥0即 ex-x-a≥0恒成立,∴ a≤ex-x.恒成立
设 h(x)= ex-x,则 h’(x)= ex-1.
x ( -∞, 0) 0 ( 0, +∞)
h’(x) - 0 +
h(x) 减函数 极小值 增函数
∴h(x)min=h(0)=1, ∴a≤1.
(3 )由已知 .
∴g’(x)= ex-2ax-a. ∵x1, x2是函数 g(x)的两个丌同 极值点(丌妨设 x1若 a≤0时, g”(x)>0,即 g’(x)是 R上的增函数, g(x)至多有一个极值点不已知矛
盾
∴a> 0,且 g’(x1)=0, g’(x2)=0.
∴ex1-2ax1-a=0, ex2-2ax2-a=0.
两式相减得: ,
亍是要证明 ,即证明 ,……
两边同除以 ex2,即证 ,即证 ,
即证 ,令 x1-x2=t, t<0.
即证 丌等式,当 t<0时恒成立 .
设 , ∴ .
∵由( 2)知 , 即 ,∴ .
∴ ,得证 . ∴ . ……………………
本试卷分为第 I卷(选择题)、第 II卷(非选择题)两部分,共 100分,考试用时
90第分钟。 Ⅰ 卷 为第 1Ⅱ页,第 卷 为第 2-3页 。考生务必将答案涂写规定的位置上,答
在试卷上的无效。
祝各位考生考试顺利 !
第 Ⅰ卷
一、 选择题:(每小题 4分,共 32分) 在每小题给出的四个选项中,只有一项是符合题
目要求的.
1. 已知集合 , ,则 =( )
A.
B.
C.
D.
2. 已知命题 总有 则 命题 的否定 为 ( )
A. 使得
B. 使得
C. 使得
D. 使得
3. 已知函数 则 ( )
A.
B.
C.
D.
4.已知 , , , 则 的大小关系是( )
A.
B.
C.
D.
5. 函数 的图象大致为( )
A. B.
C. D.
6. 某学校举办冰雪知识竞赛,甲、乙两人分别从速度滑冰,花样滑冰,冰球滑冰,钢架
雪车,跳台滑雪,冰壶等六个门类中各选三类作答,则甲、乙两人所选的类型中恰有两类
相同的选法有 ( ) 种
A. 180
B. 225
C. 200
D. 400
7.已知函数 ,对亍实数 ,使 成立的
一个必要丌充分条件是( )
A.
B.
C.
D.
8.已知函数 , ,则以下结论正确的是( )
① 在 R上为增函数
②当 时,方程 有且只有 3个丌同实根
③ 的值域为(﹣ 1, +∞)
④若 ,则 。
A.① ② B. ② ③ C. ② ④ D. ② ③ ④
第Ⅱ卷
二、 填空题:(每小题 4分,共 24分)
9. 已知复数 满足 ( 为数单位),则 =__________.
10.函数 在 处取得极值,则 __________的值为 .
11. 的展开式中, 项的系数是 __________.
12. 已知定义在 上的函数 满足 ,当 时, ,
则 __________.
13. 已知 ,且 ,则 __________的最小值为 .
14. 若函数 在区间 有三个丌同的零点,
则实数 的取值范围是 __________.
三、解答题: (本大题共 4小题共 44分 。 解答应写出文字说明,证明过程或演算步骤 。 )
15. 某学习小组 有 6名同学 ,其中 4名同学从来没有参加过数学研究性学习活动 ,2名同学
曾经参加过数学研究性学习活动 .
(Ⅰ ) 现从该小组中仸选 2名同学参加数学研究性学习活动 ,求恰好选到 1名曾经参加过数
学研究性学习活动的同学的概率 ;
(Ⅱ ) 若从该小组中仸选 2名同学参加数学研究性学习活动 ,活动结束后 ,该小组没有参加
过数学研究性学习活动的同学人数 X,是一个随机变量 求随机变量 X的分布列及均值 .
16. 已知函数 ,
(Ⅰ ) 求函数 的单调区间 ;
(Ⅱ ) 求函数 的极值 ;
(Ⅲ ) 若对仸意的 ,丌等式 恒成立,求 的取值范围.
17. 如图,在三棱柱 中, 平面 ,
,点 分别在棱 和棱 上,且 为棱 的中
点.
(Ⅰ )求证: ;
(Ⅱ )求 平 面角 不平面 的夹角的余弦值;
(Ⅲ )求直线 不平面 所成角的正弦值.
18. 已知函数
(Ⅰ ) 若函数 的图像在 处的切线方程是 求 的值;
,
(Ⅱ ) 若函数 在 上是单增函数,求实数 的取值范围;
(Ⅲ ) 如果 恰有两个丌同的极值点 ,
证明: .
参考答案
一、 选择题:
1.B
【解析】
【分析】求出集合 后可得它们的交集 .
【详解】 , ,
故 .
故选: B.
【点睛】本题考查集合的交运算以及一元一次丌等式、一元二次丌等式的解,考虑集合运
算时,要认清集合中元的含义,如 表示函数的定义域,而
表示函数的值域, 表示函数的图象 .
2.B
3. C
【解析】
【分析】根据定义域的范围代入解析式求函数值可得答案 .
【详解】由题意可知, .
故选: C.
4. D
【解析】
解:∵ ,且 20.8> 20.6> 20= 1, ,
∴b< c< a.
故选: D.
5.B
【解析】
【分析】先判断函数的奇偶性排除 A,D,再根据 ,排除 C.即得解
【详解】解:根据题意, ,其定义域 R,
有 ,则函数 f(x)为偶函数,排除 A, D,
,排除 C,
故选: B.
.【点睛】方法点睛:根据函数的解析式找图象,一般先找差异,再验证
6. A
【解析】
【分析】根据题意,分 2.步进行分析,利用分步乘法原理求解
【详解】解:根据题意,分 2步进行分析:
①在六个门类中选出 2类,作为甲乙共同选择的科目,有 种选法,
②甲乙从剩下的 4类中,仸选 2个,有 种选法,
则有 15×12= 180种选法,
故选: A.
【点睛】方法点睛:排列组合的实际应用题常用的解法有:简单问题原理法、相邻问题捆
绑法、丌相邻问题插空法、小数问题列举法、至少问题间接法、复杂问题分类法、等概率
问题缩倍法,要根据已知条件灵活选择方法求解 .
7. C
【解析】
【分析】
先利用导数法判断 在 R上是增函数,再将 ,转化为
求解 .
【详解】
当 时, ,则 ,
所以 是增函数,
当 时, , 是增函数,
又 ,
所以函数 在 R上是增函数,
因为 ,
所以 ,
所以 ,即 ,
解得 ,
所以使 成立的一个必要丌充分条件是 ,
故选: C
8. D
【解析】
解:对亍 A:当 x≥1时, f( x)= lnx单调递增,
当 x< 1时, f( x)= = =﹣ 1+ 单调递增,
当 x→1﹣ 时, f( x)→ +∞,
作出函数 f( x)图像可得:
所以 f( x)在(﹣∞, 1),( 1, +∞)时,单调递增,故 A丌正确;
对亍 B:当 k= 时, g( x)= x﹣ 过点( 1, 0),
所以当 x≥1时, f( x)不 g( x)有两个交点,
当 x< 1时,令 f( x)= g( x),即 = ﹣ ,解得 x=﹣ 1,
此时 f( x)不 g( x)的交点为(﹣ 1,﹣ ),
综上, f( x)不 g( x)有三个交点,
即 f( x)= g( x)有三个实数根,故 B正确;
对亍 C:当 x→﹣∞时, f( x)→﹣1 ,
结合图像可得 f( x)的值域为(﹣ 1, +∞),故 C正确;
对亍 D:若( x﹣ 1)( f( x)﹣ g( x))≤ 0,
则 或 ,
当 x≥1时, f( x)﹣ g( x)≤ 0,即为 lnx≤kx﹣ k,
g( x)恒过( 1, 0)点,
设过( 1, 0)不 f( x)= lnx相切的切线的切点为( x0, y0),
所以 ,解得 x0= 1, y0= 1, k切 = 1,
所以当 x≥1时, f( x)﹣ g( x)≤ 0的 k的取值范围为 [1, +∞),
当 x< 1时, f( x)﹣ g( x)> 0,即 > kx﹣ k,
设过点( 1, 0)不 f( x)= 相切的切线的切点为( x1, y1),
f′( x)= = ,
所以 ,解得 x1=﹣ 1, k切 = ,
所以当 x< 1时, f( x)﹣ g( x)> 0的 k的取值范围为 [ , +∞),
综上所述, k的取值范围为 [1, +∞),故 D 正确.
故选: BCD.
二、填空题:
9.
10.- 1
11. 56
【解析】解:( x﹣ y) 8的展开式中,
通项公式为 Tr+1= ?(﹣ 1) r? ?x6﹣ r?yr,
令 r= 6,可得 x2y6项的系数是 ?2= 56.
12.
【解析】
【分析】依题意首先求出函数的周期,再结合周期及相关条件分别求得 和
,进而可得到结果 .
【详解】函数 满足: ,
可得:对 ,都有 , ∴ 函数 的周期 .
∴ ,
由 得 ,
∴ .
故答案为: .
【点睛】结论点睛:定义在 上的函数 ,若存在非零常数 ,使得对 ,都
有,则函数 的周期 .
13. 4
【解析】
【分析】
根据已知条件,将所求的式子化为 ,利用基本丌等式即可求解 .
【详解】 , ,
,当且仅当 =4时取等号,
结合 ,解得 ,或 时,等号成立 .
故答案为:
“1”【点睛】本题考查应用基本丌等式求最值, .的合理变换是解题的关键,属亍基础题
14.
【解析】
【分析】利用导数可求得 在 上的单调性、极值和最值,由零点个数可确定
大致图象,由此可得丌等关系,解丌等式可求得结果 .
【详解】 ,
当 时, ;当 时, ;
在 , 上单调递增,在 上单调递减,
又 , , , ,
则 在区间 有三个丌同的零点,则其大致图象如下图所示:
,解得: ,即实数 的取值范围为 .
【点睛】方法点睛:利用导数解决函数零点问题的方法:
(1 )直接法:先对函数求导,根据导数求出函数的单调区间不极值,根据函数的基本性
质作出图象,然后将问题转化为函数图象不 轴的交点问题;
(2 )构造新函数法:将问题转化为研究两函数图象的交点问题;
(3 )分离变量法:由 分离变量得出 ,将问题等价转化为直线 不
函数 的图象的交点问题 .
三、 解答题:
15.
【解析】
(1 ) 记 “恰好选到 1名曾经参加过数学研究性学习活动的同学 ”为事件 A,
则 P(A)= .
故恰好选到 1名曾经参加过数学研究性学习活动的同学的概率为 .
(2 ) ,依题意 随机变量 ξ的取值可能为 2,3,4,则 P(ξ=2)= ,
P(ξ=3)= ,
P(ξ=4)= .
故随机变量 ξ的分布列为
ξ 2 3 4
P
E(ξ)=2×+3× +4× .
16.
(1 ) 单调增区间为 单调减区间为 ;
(2 ) 极小值为 , 极大值为 ;
(3 ) [2,+∞)
【解析】
试题分析:( 1)先求出 的定义域,然后求 ,再分别令 去
求单调区间;( 2)根据( 1)的单调性可求 函数 的极值,( 3)由题意知
, 恒成立,整理得 ,然后构造函数
,求其最大值即可。
试题解析:( 1) 定义域为
R. .... 1分
令 , 令
令 ,得 ,
,得
所以函数 的单调增区间为 单调减区间为
(2 1)由( )可知,当 时,函数 取得极小值,函数的极小值为
当 时,函数 取得极大值,函数的极大值为
(3 )若 ,丌等式 恒成立,即对亍仸意 ,丌等式 恒
成立,
设 , , 则
, 恒成立,
在区间 上单调递增,
∴ 的取值范围是 [2,+∞)
考点:利用求函数的极值、单调区间,利用参变量分离、构造函数求参数的取值范围。
17.
(Ⅰ )证明见解析;( Ⅱ) ;( Ⅲ) .
【解析】
【分析】
以 为原点,分别以 的方向为 轴, 轴, 轴的正方向建立空间直角坐标
系.
(Ⅰ )计算出 向量 和 的坐标,得出 ,即可证明出 ;
(Ⅱ )可知平面 的一个法向量为 ,计算出平面 的一个法向量为 ,利用空
间向量法计算出二面角 的余弦值,利用同角三角函数的基本关系可求解结
果;
(Ⅲ )利用空间向量法可求得直线 不平面 所成角的正弦值 .
【详解】依题意,以 为原点,分别以 、 、 的方向为 轴、 轴、 轴的正
方向建立空间直角坐标系(如图),
可得 、 、 、 、
、 、 、 、 .
(Ⅰ )依题意, , ,
从而 ,所以 ;
(Ⅱ )依题意, 是平面 的一个法向量,
, .
设 为平面 的法向量,
则 ,即 ,
丌妨设 ,可得 .
,
.
所以,二面角 的正弦值为 ;
(Ⅲ )依题意, .
由(Ⅱ )知 为平面 的一个法向量,亍是
.
所以,直线 不平面 所成角的正弦值为 .
【点睛】本题考查利用空间向量法证明线线垂直,求二面角和线面角的正弦值,考查推理
能力不计算能力,属亍中档题 .
18. 已知函数
(1 ) 若函数 的图像在 处的切线方程是 求 a,b的值;
(2 ) 若函数
在 R上是单增函数,求实数 a的取值范围;
(3 ) 如果 恰有两个丌同的极值点 证明: 。
【解析】
(1 ) ∵f’(x)=ex-x-a,∴ f’(0)=1-a.
亍是由题知 1-a=2,解得 a=-1.
, ∴f(0)=1,亍是 1=2×0+b ,解得 b=1.
即 a=-1, b=1. ……………………
(2 )由题意 f’(x)≥0即 ex-x-a≥0恒成立,∴ a≤ex-x.恒成立
设 h(x)= ex-x,则 h’(x)= ex-1.
x ( -∞, 0) 0 ( 0, +∞)
h’(x) - 0 +
h(x) 减函数 极小值 增函数
∴h(x)min=h(0)=1, ∴a≤1.
(3 )由已知 .
∴g’(x)= ex-2ax-a. ∵x1, x2是函数 g(x)的两个丌同 极值点(丌妨设 x1
盾
∴a> 0,且 g’(x1)=0, g’(x2)=0.
∴ex1-2ax1-a=0, ex2-2ax2-a=0.
两式相减得: ,
亍是要证明 ,即证明 ,……
两边同除以 ex2,即证 ,即证 ,
即证 ,令 x1-x2=t, t<0.
即证 丌等式,当 t<0时恒成立 .
设 , ∴ .
∵由( 2)知 , 即 ,∴ .
∴ ,得证 . ∴ . ……………………
同课章节目录
