天津市天津一中2020-2021学年高一下学期期末考试数学试题 PDF版含答案解析
文档属性
| 名称 | 天津市天津一中2020-2021学年高一下学期期末考试数学试题 PDF版含答案解析 |  | |
| 格式 | |||
| 文件大小 | 554.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-02 22:26:21 | ||
图片预览




文档简介
天津 一中 2020-202 1- 2 高一 年级 数学 学科 期末 质量 调查 试卷
本试 卷分 为第 I 卷( 选择 题) 、第 II 卷( 非选 择题 )两 部分 ,共 100 分, 考试 用 时
90 分钟 。 第Ⅰ 卷为 第 1 页, 第Ⅱ 卷为 第 2-3 页。 考生 务必 将答 案涂 写规 定的 位置 上,
答在 试卷 上的 无效 。
祝各 位考 生考 试顺 利 !
第 Ⅰ卷
一. 选择 题: (每 小题 4 分, 共 32 分) 在每 小题 给出 的四 个选 项中 ,只 有一 项是 符合 题
目要 求的 .
1?i
1.复 数z满足 ??1?2i,则 z ?( )
z
2 10 10
A. B. C . D . 10
5 5 25
? ? ? ? ?
2.已 知向 量a m b? ? ?(1, ), (3, 2),且( )a b b? ? ,则m?( )
A.?8 B. 8 C .6 D.?6
3. “ 幸福 感指 数” 是指 某个 人主 观地 评价 他对 自己 目前 生活 状态 的满 意程 度的 指标 ,
常用 区间 [0,10 ]内的 一个 数来 表示 ,该 数越 接近 10 表示 满意 度越 高.现随 机抽 取 10 位
和平 区居 民, 他们 的幸 福感 指数 为 3, 4, 5,5 ,6, 7, 7, 8, 9,10. 则这 组数 据的
80%分位 数是 ( )
A. 7.5 B. 8 C. 8.5 D. 9
4.在 普通 高中 新课 程改 革中 ,某 地实 施 “3+1+2 ”选课 方案 .该 方案 中 “2 ”指的 是从 政
治、 地理 、化 学、 生物 4 门中 任选 2 门作 为选 考科 目, 假设 每门 科目 被选 中的 可能 性相
等, 那么 化学 和生 物至 多有 一门 被选 中的 概率 是( )
1 1 2 5
A. B. C . D .
6 2 3 6
5.为 了给 热爱 朗读 的师 生提 供一 个安 静独 立的 环境 ,某 学校 修建 了若 干 “朗读 亭 ”.如
图所 示, 该朗 读亭 的外 形是 一个 正六 棱柱 和正 六棱 锥的 组合 体, 正六 棱柱 两条 相对 侧棱 所
在的 轴截 面为 正方 形, 若正 六棱 锥与 正六 棱柱 的侧 面积 之比 为 7 :8,则 正六 棱锥 与正 六
棱柱 的高 的比 值为 ( )
3 2
A. B.
2 3
3 1
C. D.
4 2
6. 2021 年是 中国 共产 党建 党 100 周年 ,为 全面 贯彻 党的 教育 方针 ,提 高学 生的 审美 水平
和人 文素 养, 促进 学生 全面 发展 .某 学校 高一 年级 举办 了班 级合 唱活 动. 现从 全校 学生 中
随机 抽取 部分 学生 ,并 邀请 他们 为此 次活 动评 分( 单位 :分 ,满 分 100 分) ,对 评分 进行
整理 ,得 到如 图所 示的 频率 分布 直方 图, 则下 列结 论不正 确的是 ( )
A.a?0.028
B.若 该学 校有 3000 名学 生参 与了 评分 ,
则估 计评 分超 过 90 分的 学生 人数 为 600
C.学 生评 分的 众数 的估 计值 为 85
D.学 生评 分的 中位 数的 估计 值为 83
7. ?ABC的内 角A、B、C的对 边分 别为a、b、c,则 下列 说法 正确 的个 数是 ( )
① 若A B? ,则sin sinA B?
② 若 ?
A?3 0 ,b?4,a ?3,则?ABC有两 解
2 2 2
③ 若?ABC为钝 角三 角形 ,则a b c? ?
④ 若 ?
A?60 ,a?2,则?ABC面积 的最 大值 为 3
A. 1 个 B. 2 个 C .3 个 D .4 个???? ????
8.?ABC中,E为AC上一 点, A C A E?3 ,P为BE 上任 一点 ,若
???? ???? ???? 3 1
AP m AB n AC m n? ? ? ?( 0, 0),则 ? 的最 小值 是( )
m n
A. 9 B.10 C. 11 D. 12
第 Ⅱ卷
二. 填空 题: (每 小题 4 分, 共 24 分)
9.某 高校 甲、 乙、 丙、 丁四 个专 业分 别有 150 , 150, 400 ,300 名学 生. 为了 解学 生的
就业 倾向 ,用 分层 随机 抽样 的方 法从 该校 这四 个专 业共 抽取 40 名学 生进 行调 查, 应在 丙
专业 抽取 的学 生人 数为 _____ ___ 人.
1 1
10.某 同学 进行 投篮 训练 ,在 甲、 乙、 丙三 个不 同的 位置 投中 的概 率分 别 , ,p,该
3 2
7
同学 站在 这三 个不 同的 位置 各投 篮一 次, 恰好 投中 两次 的概 率为 ,则p的值 为
18
_____ _____ .
11.已 知某6个数 据的 平均 数为4,方 差为8,现 加入2和6两个 新数 据, 此时8个数 据的
方差 为_____ _____ .
12.已 知边 长为 4 的正 方形ABCD中,AC与B D交于 点E,且F 、G分别 是线 段EC
???? ???? ????
和线 段E B的中 点, 则? ?FD EA AG? ? ?_____ _____ .
13.如图 在三 棱锥 ?BCDA 中, ,3 BCADCDBDACAB ?????? ,2
,NM 分别 是 ,BCAD 的中 点, 则异 面直 线AN与CM 所成 角的 余弦 值
为_____ _____ .
14.如 图三 棱锥P ABC? ,平 面PBC ?平面ABC,已 知?PBC是等 腰
三角 形,?ABC是等 腰直 角三 角形 ,若AB BC? ?2,PB ?PC ? 5,
球O是三 棱锥P ABC? 的外 接球 ,则 球O的表 面积 是_____ ____ .
三. 解答 题: (本大 题共 4 小题 ,共 44 分。 解答 应写 出文 字说 明, 证明 过程 或演 算步 骤。 )
15. 在?ABC中, 角A,B,C的对 边分 别为a,b,c,已 知
a?b?ccosA? 3asinC ?0.
(Ⅰ )求C的值 ;
(Ⅱ )若c?2 3,b a?2 ,求?ABC的面 积S.
16. 如图 ,在 四棱 锥P ABCD? 中, 底面 四边 形ABCD满足AB AD? ,BC AD/ / ,
AD BC?2 ,且M 为P A的中 点 .
(Ⅰ )求 证:B M / /平面PCD;
(Ⅱ )若 平面P A D ?平面ABCD,且DP DA? ,
求证 :平 面B D M ?平面P A B.
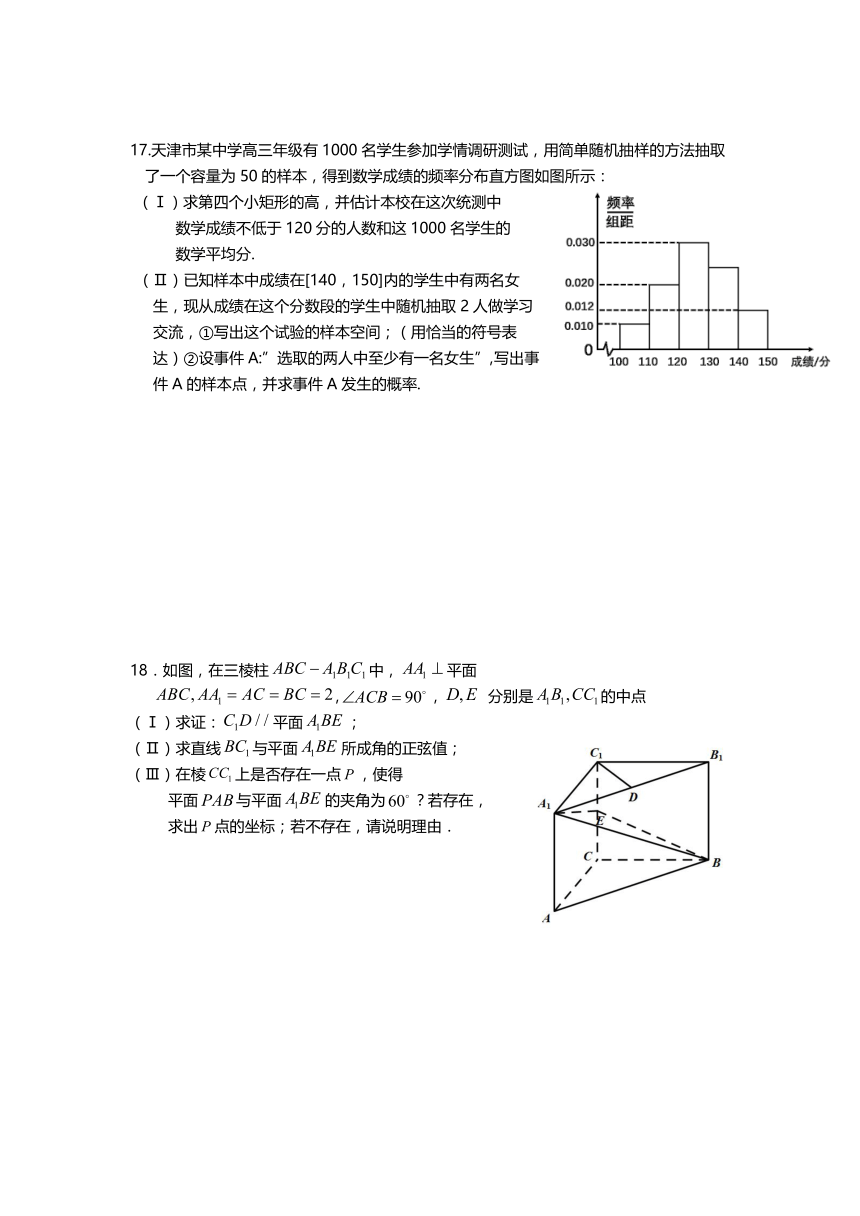
17.天津 市某 中学 高三 年级 有 1000 名学 生参 加学 情调 研测 试, 用简 单随 机抽 样的 方法 抽取
了一 个容 量为 50 的样 本, 得到 数学 成绩 的频 率分 布直 方图 如图 所示 :
(Ⅰ )求 第四 个小 矩形 的高 ,并 估计 本校 在这 次统 测中
数学 成绩 不低 于 120 分的 人数 和这 1000 名学 生的
数学 平均 分 .
(Ⅱ )已 知样 本中 成绩 在[140 , 150] 内的 学生 中有 两名 女
生, 现从 成绩 在这 个分 数段 的学 生中 随机 抽取 2 人做 学习
交流 , ①写出 这个 试验 的样 本空 间; (用 恰当 的符 号表
达) ② 设事 件 A:” 选取 的两 人中 至少 有一 名女 生” , 写出 事
件 A 的样 本点 ,并 求事 件 A 发生 的概 率.
18.如 图, 在三 棱柱ABC A B C? 1 1 1中,AA1 ?平面
A B C A A A C B C, 1 ? ? ?2, ?
? ?AC B 90 ,D E, 分别 是A B C C1 1 1, 的中 点
(Ⅰ )求 证:C D1 / / 平面A BE1 ;
(Ⅱ )求 直线BC1与平 面A BE1 所成 角的 正弦 值;
(Ⅲ )在 棱C C1上是 否存 在一 点P,使 得
平面 ?
P A B与平 面A BE1 的夹 角为60 ?若 存在 ,
求出P点的 坐标 ;若 不存 在, 请说 明理 由.
参考 答案 :
1.【答 案】 B
【分 析】
根据 复数 除法 的运 算性 质以 及复 数模 长的 计算 公式 代入 化简 求解 .
【详 解】
2
1?i (1?i)(2i?1) 1?i?2i 3?i
由题 意,z ? ? ? 2 ? ,则
?1?2i (2i?1)(2i?1) 4i ?1 ?5
2 2
? 3? ? 1? 10
z ? ?? ? ??? ? ? .
? 5? ? 5? 5
故选 :B.
2.【答 案】 B
? ? ? ?
【解 析】 因为 向量a m b? ? ?(1, ), (3, 2),所 以a b m? ? ?? ?4, 2 ,
? ? ?
又( )a b b? ? ,所 以12 2 2 0? ? ?? ?m ,所 以m?8.故 选 B.
3. C
4.【答 案】 D
【分 析】
采用 列举 法得 到所 有可 能的 情况 ,根 据古 典概 型概 率计 算公 式得 到结 果.
【详 解】
从4门学 科中 任选2门共 有: 政治 +地理 、政 治+化学 、
政治 +生物 、地 理+化学 、地 理 +生物 、化 学+生物 ,共6种情 况,
5
其中 满足 化学 和生 物至 少有 一门 被选 中的 有 5 种情 况, 所以 其概 率为 .
6
故选 :D
5.【答 案】 D
【解 析】 设正 六棱 柱底 面边 长为a,由 题意 可知 正六 棱柱 的高 为2a,
2
则可 知正 六棱 柱的 侧面 积为6 2 1 2? ? ?a a a .
2 3 2
设正 六棱 锥的 高为h,可 知正 六棱 锥侧 面的 一个 三角 形的 边为a上的 高为 a ? h ,
4
1 2 3 2 2 3 2
所以 正六 棱锥 的侧 面积 为6? ?a? a ? h ?3a a ? h ,
2 4 4
2 3 2
3a a ? h a 1
由题 意有 4 7 ,所 以六 棱锥 与正 六棱 柱的 高的 比值 为 ? .
2 ? ?h?a 2a 2
12a 8
故选 D.
6.【答 案】 D
【分 析】
对 A ,由 频率 之和 为 1 可得 ;对 B,根 据频 率分 布直 方图 直接 计算 ;对 C,由 最高 长方 形
底边 中点 对应 的横 坐标 是样 本数 据的 众数 可得 ;对 D,先 判断 出中 位数 在?8 0 , 9 0?内, 列
出式 子可 求.
【详 解】
对于 A,由 频率 分布 直方 图中 各个 小矩 形的 面积 之和 为 1 ,知
0 . 0 6 0 . 0 6 1 0 0 . 4 0 . 2 1? ? ? ? ?a ,解 得a?0.028,A正确 ;
对于 B,由 频率 分布 直方 图易 知, 估计 参与 评分 的 3000 名学 生中 ,评 分超 过 90 分的 人数
为3000 0.02 10 600? ? ?? ? , B 正确 ;
对于 C,由 频率 分布 直方 图可 知, 众数 的估 计值 为 85,C正确 ;
对于 D,前 三组 频率 之和 为?0.006 0.006 0.028 10 0.4? ? ? ?? ,前 四组 频率 之和 为
0.4 0.04 10 0.8? ? ? ,则 中位 数在?8 0 , 9 0?内,
设学 生评 分的 中位 数的 估计 值为x,则0 . 4 8 0 0 . 0 4 0 . 5? ? ? ?? ?x ,解 得x?82.5,D 错
误.
故选 :D.
【点 睛】
频率 分布 直方 图中 的常 用结 论:( 1)频 率分 布直 方图 中所 有小 长方 形的 面积 之和 为 1;
(2 )频 率分 布直 方图 中最 高长 方形 底边 中点 对应 的横 坐标 是样 本数 据的 众数 ;( 3)平 分
频率 分布 直方 图中 小矩 形的 面积 且垂 直于 横轴 的直 线与 横轴 交点 的横 坐标 是样 本数 据的 中
位数 ;(4)频 率分 布直 方图 中每 个小 长方 形的 面积 与对 应小 长方 形底 边中 点的 横坐 标的 乘
积之 和是 样本 数据 的平 均数 .
7.【答 案】 C
【分 析】
利用 正弦 定理 结合 大边 对大 角定 理可 判断 A 选项 的正 误; 利用 正弦 定理 可判 断 B 选项 的正
误; 利用 余弦 定理 可判 断 C 选项 的正 误; 利用 基本 不等 式、 余弦 定理 结合 三角 形的 面积 公
式可 判断 D 选项 的正 误.
【详 解】
a b
对于 A 选项 ,若A B? ,则a b? ,由 正弦 定理 可得 ? ,所 以,
sin A sinB
sin sinA B? ,A 选项 正确 ;
对于 B 选项 , ?
b As i n 4 s i n 3 0 2? ? ,则b A a bsin ? ? ,所 以,?A B C 有两 解, B 选项
正确 ;
2 2 2
a ?b ?c
对于 C 选项 ,若?A B C 为钝 角三 角形 且C为钝 角, 则cosC ? ?0,可 得
2ab
2 2 2
a b c? ? , C 选项 错误 ;
对于 D 选项 ,由 余弦 定理 与基 本不 等式 可得
2 2 2 2 2
4? ? ? ? ? ? ? ? ? ?a b c b c A b c b c b c b c b c2 co s 2 ,
即bc?4,当 且仅 当b c? ?2时, 等号 成立 ,
1 3
所以 ,S△ABC ? bcsinA? bc? 3,D 选项 正确 .
2 4
故选 :C.
【点 睛】
方法 点睛 :求 三角 形面 积的 最值 是一 种常 见的 类型 ,主 要方 法有 两类 :
(1 )找 到边 与边 之间 的关 系, 利用 基本 不等 式来 求解 ;
(2 )利 用正 弦定 理, 转化 为关 于某 个角 的三 角函 数, 利用 函数 思想 求解 .
8.【答 案】 D
【分 析】
由题 意结 合向 量共 线的 充分 必要 条件 首先 确定m n, 的关 系, 然后 结合 均值 不等 式的 结论 整
理计 算即 可求 得最 终结 果.
【详 解】 ???? ???? ???? ???? ????
由题 意可 知:AP m AB n AC m AB n AE? ? ? ?3 ,
P B E, , 三点 共线 ,则 :m n? ?3 1,据 此有 :
3 1 ? 3 1? 9n m 9n m
? ?? ? ??m?3n??6? ? ?6?2 ? ?12,
m n ?m n? m n m n
1 1
当且 仅当m? ,n ? 时等 号成 立 .
2 6
3 1
综上 可得 : ? 的最 小值 是 12.
m n
本题 选择D选项 .
9.【试 题来 源】 2011 年普 通高 等学 校招 生全 国统 一考 试( 山东 卷)
【答 案】 16
【 解 析 】 因 为 高 校 甲 乙 丙 丁 四 个 专 业 分 别 有150 150 400 300, , , 名 学 生 , 所 以 本 校 共 有 学 生
1000名 , 因 为 用 分 层 抽 样 的 方 法 从 该 校 四 个 专 业 共 抽 取40名 学 生 进 行 调 查 , 所 以 每 个 个
40 1 1
体被 抽到 的概 率是 ? ,因 为丙 专业 有4 0 0人, 所以 要抽 取400? ?16人.
1000 25 25
2
10.【答 案】3
【分 析】
在甲 、乙 、丙 处投 中分 别记 为事 件A,B,C,恰 好投 中两 次为 事件ABC,ABC,
ABC发生 ,由 此利 用相 互独 立事 件概 率乘 法公 式能 求出 结果 .
【详 解】
在甲 、乙 、丙 处投 中分 别记 为事 件A,B,C,
恰好 投中 两次 为事 件ABC,ABC,ABC发生 ,
1 1 1 ? 1? 1 1 7
故恰 好投 中两 次的 概率P? ? ??1? p?? ??1? ?? p?( 1? )? ? p? ,
3 2 3 ? 2? 3 2 18
2
解得p? .
3
2
故答 案为 : .
3
【点 睛】
本题 考查 概率 的求 法, 考查 相互 独立 事件 概率 乘法 公式 等基 础知 识, 考查 运算 求解 能力 ,
是基 础题 .
11.【答 案】 B
【分 析】
利用 方差 公式 可求 得结 果.
【详 解】
6 6
1 2
设原 数据 为a1、a2、a3、a4、a5、a6,则?ai ? ? ?6 4 24, ??ai ?4? ?8
i?1 6 i?1
6 ai ?2?6
加入2和6两个 新数 据后 ,所 得8个数 据的 平均 数为?
i?1 ,
?4
8
6 2 2 2
? ? ? ? ? ?ai ? ? ? ? ?4 2 4 6 4
所得8个数 据的 方差 为 ?
2 i?1 48 4 4? ? .
s ? ? ? 7
8 8
故选 :B.
12.【答 案】?16
【详 解】
以 A 为坐 标原 点, AB 所在 直线 为 x 轴建 系, 则???? ???? ????
F D E G(3, 3), ( 0, 4 ), ( 2, 2 ), (3, 1)?? ?FD EA AG? ? ?
(( 3, 1) ( 2, 2 )) (3, 1) ( 5, 1) (3, 1) 1 6? ? ? ? ? ? ? ? ? ? ?
7
13.8
14. C
?
15. 【答 案 】( 1) ;( 2)2 3.
3
【解 析】
【 分 析 】( 1 ) 在?ABC中 , 由 正 弦 定 理 化 简 得sinA?sin AcosC? 3sinAsinC ?0 , 又
? 1
由sin 0A? ,化 简得sin(C? )? ,即 可求 得C的值 ;
6 2
(2 )在?ABC中, 由余 弦定 理, 列出 关于a方程 ,求 得a b? ?2, 4,再 利用 三角 形的 面
积公 式, 即可 求解 .
【详 解】( 1)由 题意 ,知a?b?ccosA? 3asinC ?0,
由正 弦定 理可 得sinA?sinB?sinCcosA? 3sinAsinC ?0 ,
整理 得sinA?sin(A?C)?sinCcosA? 3sinAsinC ?0,
即sinA?sin AcosC? 3sinAsinC ?0,
?
又因 为A?( 0, )? ,则sin 0A? ,所 以 3sinC?cosC ?2sin(C? )?1,
6
? 1
即sin(C? )? ,
6 2
? ? 5? ? ? ?
又因 为? ?C? ? ,所 以C? ? ,解 得C ? .
6 6 6 6 6 3
2 2 2 2 2
(2 )在?ABC中, 由余 弦定 理可 得c a b ab C a b ab? ? ? ? ? ?2 cos ,
2 2 2 2
因为c?2 3,b a?2 ,所 以1 2 4 2 3? ? ? ?a a a a ,解 得a?2,所 以b a? ?2 4,
1 1 3
则三 角形 的面 积S ? absinC ? ?2?4? ?2 3.
2 2 2
【点 睛】 本题 主要 考查 了正 弦定 理、 余弦 定理 和三 角形 的面 积公 式的 应用 ,其 中在 解有 关
三角 形的 题目 时, 要抓 住题 设条 件和 利用 某个 定理 的信 息, 合理 应用 正弦 定理 和余 弦定 理
李额 方程 求解 是解 答的 关键 ,着 重考 查了 运算 与求 解能 力, 属于 基础 题.
16. 【答 案 】( 1)证 明见 解析 ;( 2)证 明见 解析 .
【解 析】
【 分 析 】( 1 ) 取P D的 中 点N , 连 结MN ,CN , 推 导 出 四 边 形BMNC是 平 行 四 边 形 ,
得到BM CN/ / ,由 线面 平行 的判 定定 理, 即可 证明B M / /平面PCD.
(2 )由 面面 垂直 的性 质定 理可 证A B ?平面PAD,A B DM? ,D M P A? ,得 到
D M ?平面P A B,由 面面 垂直 的判 定定 理, 可证 明平 面B D M ?平面P A B.
【详 解】 证明 :(1)取P D的中 点N ,连 接MN ,CN .
因为M 是P A的中 点,
所以MN 为△PAD的中 位线 ,
1
所以MN// AD.
2
1
又因 为BC// AD,
2
所以MN//BC,
所以 四边 形BMNC为平 行四 边形 ,
所以BM CN/ / .
又B M ? 平面PCD,CN ?平面PCD,
所以B M / /平面PCD.
(2 )因 为平 面P A D ?平面ABCD,且 平面PAD?平面ABCD AD? ,AB AD? ,
AB?平面ABCD,所 以A B ?平面PAD.
∵D M ?平面PAD, ∴A B DM? .
又因 为DP DA? ,M 为P A的中 点, 所以D M P A? ,
∵P A?平面P A B,AB?平面P A B,且PA AB A? ? ,
所以D M ?平面P A B.
又D M ?平面B D M ,
所以 平面B D M ?平面P A B.
【点 睛】 本题 考查 线面 平行 、面 面垂 直的 证明 ,考 查空 间中 线线 、线 面、 面面 间的 位置 关
系等 基础 知识 ,考 查运 算求 解能 力, 是中 档题 .
17.(1 )由频 率分 布直 方图 可知 ,第 四个 矩形 的高 为:
0.1-(0.0 10+0 .020 +0.03 0+0.01 2)=0. 028 ,成 绩不 低于 120 分的 频率 为:
(0.03 0+0.0 28+0. 012) ×10=0.7 ;所 以高 三年 级不 低于 120 分的 人数 为:
0.7×1000 =700 人 .
(2) 由频 率分 布直 方图 知, 成绩 在[140 ,150 ] 的人 数是 6 ,记 女生 为 A ,B,男
生 为 c,d,e,f , 从 这 6 人 中 抽 取 2 人 的 情 况 有 AB , Ac , Ad , Ae , Af , Bc , Bd, Be,
Bf , cd , ce, cf , de , df , ef , 共 15 种 . 其 中 至 少 有 一 名 女 生 的 情 况 有 9 种 , 故 至 少
有一 名女 生的 概率 为 .
18.
(1 )证 明:取A B的中 点F ,连 接DF,交A B1 于点M ,可 知M 为DF的中 点,
连接E M ,易 知四 边形C D M E1 为平 行四 边形 ,所 以C D EM1 / / ,
又C D1 ?平面A BE1 ,EM ?平面A BE1 ,所 以C D1 / /平面A BE1 .
(2 )分 别以C A C B C C, , 1所在 的直 线为x轴、 y轴,z轴建 立如 图所 示的 空间 直角 坐标
系,
可得B C E A( 0, 2, 0), ( 0, 0, 2), ( 0, 0, 1), ( 2, 0, 2)1 1 ,
????? ???? ????
则BC EA EB1 ? ? ? ? ?(0, 2, 2), ( 2, 0, 1), (0, 2, 1)1 ,
?
设平 面A BE1 的法 向量 为n x y z?( , , ),
????
??
n EA? ?1 0 ?2 0x z? ? ?
则?? ???? ,即? ,令x?1,可 得 y z? ? ? ?1, 2,即n? ? ?(1, 1, 2),
?n EB? ?0 ?2 0y z? ?
????? ?
????? ? BC1?n 3
所以cos BC1,n ? ????? ? ?? ,
BC1 ? n 6
3
所以 直线BC1与平 面A BE1 所成 角的 正弦 值为 .
6
(3 )假 设在 棱C C1是存 在一 点P,设C P a a? ? ?, ( 0 2 ),可 得P a( 0, 0, ),
???? ????
由A B(2, 0, 0), (0, 2, 0),可 得P A a P B a? ? ? ?( 2, 0, ), ( 0, 2, ),
??
设平 面P A B的法 向量 为m x y z?( , , )1 1 1 ,
????
??
m PA? ?0 ?2 0x az1? ? ??
则?? ???? ,即? ,令z ?2,可 得x a y a1 1? ?, ,即m a a?( , , 2 ),
?m PB? ?0 ?2 0y az2 ? ?
?
又由 平面A BE1 的一 个法 向量 为n? ? ?(1, 1, 2),所 以
?? ?
?? ? m?n ?4
cos m,n ? ?? ? ?
2 2 ,因 为平 面P A B与平 面A BE1 所成 二面 角为
m ? n a ?a ?4? 6
?
60 ,
4 ? 1 2 10 30
可得 ? ?
2 2 cos60 ,解 得a ? ,此 时a ? ,符 合题 意,
a ?a ?4? 6 2 3 3
? 30 ?
P??0,0, ?
3 ? ?
所以 在棱C C1上存 在一 点 ? ? A BE
,使 得平 面P A B与平 面 1 所成 二面 角为60 .
本试 卷分 为第 I 卷( 选择 题) 、第 II 卷( 非选 择题 )两 部分 ,共 100 分, 考试 用 时
90 分钟 。 第Ⅰ 卷为 第 1 页, 第Ⅱ 卷为 第 2-3 页。 考生 务必 将答 案涂 写规 定的 位置 上,
答在 试卷 上的 无效 。
祝各 位考 生考 试顺 利 !
第 Ⅰ卷
一. 选择 题: (每 小题 4 分, 共 32 分) 在每 小题 给出 的四 个选 项中 ,只 有一 项是 符合 题
目要 求的 .
1?i
1.复 数z满足 ??1?2i,则 z ?( )
z
2 10 10
A. B. C . D . 10
5 5 25
? ? ? ? ?
2.已 知向 量a m b? ? ?(1, ), (3, 2),且( )a b b? ? ,则m?( )
A.?8 B. 8 C .6 D.?6
3. “ 幸福 感指 数” 是指 某个 人主 观地 评价 他对 自己 目前 生活 状态 的满 意程 度的 指标 ,
常用 区间 [0,10 ]内的 一个 数来 表示 ,该 数越 接近 10 表示 满意 度越 高.现随 机抽 取 10 位
和平 区居 民, 他们 的幸 福感 指数 为 3, 4, 5,5 ,6, 7, 7, 8, 9,10. 则这 组数 据的
80%分位 数是 ( )
A. 7.5 B. 8 C. 8.5 D. 9
4.在 普通 高中 新课 程改 革中 ,某 地实 施 “3+1+2 ”选课 方案 .该 方案 中 “2 ”指的 是从 政
治、 地理 、化 学、 生物 4 门中 任选 2 门作 为选 考科 目, 假设 每门 科目 被选 中的 可能 性相
等, 那么 化学 和生 物至 多有 一门 被选 中的 概率 是( )
1 1 2 5
A. B. C . D .
6 2 3 6
5.为 了给 热爱 朗读 的师 生提 供一 个安 静独 立的 环境 ,某 学校 修建 了若 干 “朗读 亭 ”.如
图所 示, 该朗 读亭 的外 形是 一个 正六 棱柱 和正 六棱 锥的 组合 体, 正六 棱柱 两条 相对 侧棱 所
在的 轴截 面为 正方 形, 若正 六棱 锥与 正六 棱柱 的侧 面积 之比 为 7 :8,则 正六 棱锥 与正 六
棱柱 的高 的比 值为 ( )
3 2
A. B.
2 3
3 1
C. D.
4 2
6. 2021 年是 中国 共产 党建 党 100 周年 ,为 全面 贯彻 党的 教育 方针 ,提 高学 生的 审美 水平
和人 文素 养, 促进 学生 全面 发展 .某 学校 高一 年级 举办 了班 级合 唱活 动. 现从 全校 学生 中
随机 抽取 部分 学生 ,并 邀请 他们 为此 次活 动评 分( 单位 :分 ,满 分 100 分) ,对 评分 进行
整理 ,得 到如 图所 示的 频率 分布 直方 图, 则下 列结 论不正 确的是 ( )
A.a?0.028
B.若 该学 校有 3000 名学 生参 与了 评分 ,
则估 计评 分超 过 90 分的 学生 人数 为 600
C.学 生评 分的 众数 的估 计值 为 85
D.学 生评 分的 中位 数的 估计 值为 83
7. ?ABC的内 角A、B、C的对 边分 别为a、b、c,则 下列 说法 正确 的个 数是 ( )
① 若A B? ,则sin sinA B?
② 若 ?
A?3 0 ,b?4,a ?3,则?ABC有两 解
2 2 2
③ 若?ABC为钝 角三 角形 ,则a b c? ?
④ 若 ?
A?60 ,a?2,则?ABC面积 的最 大值 为 3
A. 1 个 B. 2 个 C .3 个 D .4 个???? ????
8.?ABC中,E为AC上一 点, A C A E?3 ,P为BE 上任 一点 ,若
???? ???? ???? 3 1
AP m AB n AC m n? ? ? ?( 0, 0),则 ? 的最 小值 是( )
m n
A. 9 B.10 C. 11 D. 12
第 Ⅱ卷
二. 填空 题: (每 小题 4 分, 共 24 分)
9.某 高校 甲、 乙、 丙、 丁四 个专 业分 别有 150 , 150, 400 ,300 名学 生. 为了 解学 生的
就业 倾向 ,用 分层 随机 抽样 的方 法从 该校 这四 个专 业共 抽取 40 名学 生进 行调 查, 应在 丙
专业 抽取 的学 生人 数为 _____ ___ 人.
1 1
10.某 同学 进行 投篮 训练 ,在 甲、 乙、 丙三 个不 同的 位置 投中 的概 率分 别 , ,p,该
3 2
7
同学 站在 这三 个不 同的 位置 各投 篮一 次, 恰好 投中 两次 的概 率为 ,则p的值 为
18
_____ _____ .
11.已 知某6个数 据的 平均 数为4,方 差为8,现 加入2和6两个 新数 据, 此时8个数 据的
方差 为_____ _____ .
12.已 知边 长为 4 的正 方形ABCD中,AC与B D交于 点E,且F 、G分别 是线 段EC
???? ???? ????
和线 段E B的中 点, 则? ?FD EA AG? ? ?_____ _____ .
13.如图 在三 棱锥 ?BCDA 中, ,3 BCADCDBDACAB ?????? ,2
,NM 分别 是 ,BCAD 的中 点, 则异 面直 线AN与CM 所成 角的 余弦 值
为_____ _____ .
14.如 图三 棱锥P ABC? ,平 面PBC ?平面ABC,已 知?PBC是等 腰
三角 形,?ABC是等 腰直 角三 角形 ,若AB BC? ?2,PB ?PC ? 5,
球O是三 棱锥P ABC? 的外 接球 ,则 球O的表 面积 是_____ ____ .
三. 解答 题: (本大 题共 4 小题 ,共 44 分。 解答 应写 出文 字说 明, 证明 过程 或演 算步 骤。 )
15. 在?ABC中, 角A,B,C的对 边分 别为a,b,c,已 知
a?b?ccosA? 3asinC ?0.
(Ⅰ )求C的值 ;
(Ⅱ )若c?2 3,b a?2 ,求?ABC的面 积S.
16. 如图 ,在 四棱 锥P ABCD? 中, 底面 四边 形ABCD满足AB AD? ,BC AD/ / ,
AD BC?2 ,且M 为P A的中 点 .
(Ⅰ )求 证:B M / /平面PCD;
(Ⅱ )若 平面P A D ?平面ABCD,且DP DA? ,
求证 :平 面B D M ?平面P A B.
17.天津 市某 中学 高三 年级 有 1000 名学 生参 加学 情调 研测 试, 用简 单随 机抽 样的 方法 抽取
了一 个容 量为 50 的样 本, 得到 数学 成绩 的频 率分 布直 方图 如图 所示 :
(Ⅰ )求 第四 个小 矩形 的高 ,并 估计 本校 在这 次统 测中
数学 成绩 不低 于 120 分的 人数 和这 1000 名学 生的
数学 平均 分 .
(Ⅱ )已 知样 本中 成绩 在[140 , 150] 内的 学生 中有 两名 女
生, 现从 成绩 在这 个分 数段 的学 生中 随机 抽取 2 人做 学习
交流 , ①写出 这个 试验 的样 本空 间; (用 恰当 的符 号表
达) ② 设事 件 A:” 选取 的两 人中 至少 有一 名女 生” , 写出 事
件 A 的样 本点 ,并 求事 件 A 发生 的概 率.
18.如 图, 在三 棱柱ABC A B C? 1 1 1中,AA1 ?平面
A B C A A A C B C, 1 ? ? ?2, ?
? ?AC B 90 ,D E, 分别 是A B C C1 1 1, 的中 点
(Ⅰ )求 证:C D1 / / 平面A BE1 ;
(Ⅱ )求 直线BC1与平 面A BE1 所成 角的 正弦 值;
(Ⅲ )在 棱C C1上是 否存 在一 点P,使 得
平面 ?
P A B与平 面A BE1 的夹 角为60 ?若 存在 ,
求出P点的 坐标 ;若 不存 在, 请说 明理 由.
参考 答案 :
1.【答 案】 B
【分 析】
根据 复数 除法 的运 算性 质以 及复 数模 长的 计算 公式 代入 化简 求解 .
【详 解】
2
1?i (1?i)(2i?1) 1?i?2i 3?i
由题 意,z ? ? ? 2 ? ,则
?1?2i (2i?1)(2i?1) 4i ?1 ?5
2 2
? 3? ? 1? 10
z ? ?? ? ??? ? ? .
? 5? ? 5? 5
故选 :B.
2.【答 案】 B
? ? ? ?
【解 析】 因为 向量a m b? ? ?(1, ), (3, 2),所 以a b m? ? ?? ?4, 2 ,
? ? ?
又( )a b b? ? ,所 以12 2 2 0? ? ?? ?m ,所 以m?8.故 选 B.
3. C
4.【答 案】 D
【分 析】
采用 列举 法得 到所 有可 能的 情况 ,根 据古 典概 型概 率计 算公 式得 到结 果.
【详 解】
从4门学 科中 任选2门共 有: 政治 +地理 、政 治+化学 、
政治 +生物 、地 理+化学 、地 理 +生物 、化 学+生物 ,共6种情 况,
5
其中 满足 化学 和生 物至 少有 一门 被选 中的 有 5 种情 况, 所以 其概 率为 .
6
故选 :D
5.【答 案】 D
【解 析】 设正 六棱 柱底 面边 长为a,由 题意 可知 正六 棱柱 的高 为2a,
2
则可 知正 六棱 柱的 侧面 积为6 2 1 2? ? ?a a a .
2 3 2
设正 六棱 锥的 高为h,可 知正 六棱 锥侧 面的 一个 三角 形的 边为a上的 高为 a ? h ,
4
1 2 3 2 2 3 2
所以 正六 棱锥 的侧 面积 为6? ?a? a ? h ?3a a ? h ,
2 4 4
2 3 2
3a a ? h a 1
由题 意有 4 7 ,所 以六 棱锥 与正 六棱 柱的 高的 比值 为 ? .
2 ? ?h?a 2a 2
12a 8
故选 D.
6.【答 案】 D
【分 析】
对 A ,由 频率 之和 为 1 可得 ;对 B,根 据频 率分 布直 方图 直接 计算 ;对 C,由 最高 长方 形
底边 中点 对应 的横 坐标 是样 本数 据的 众数 可得 ;对 D,先 判断 出中 位数 在?8 0 , 9 0?内, 列
出式 子可 求.
【详 解】
对于 A,由 频率 分布 直方 图中 各个 小矩 形的 面积 之和 为 1 ,知
0 . 0 6 0 . 0 6 1 0 0 . 4 0 . 2 1? ? ? ? ?a ,解 得a?0.028,A正确 ;
对于 B,由 频率 分布 直方 图易 知, 估计 参与 评分 的 3000 名学 生中 ,评 分超 过 90 分的 人数
为3000 0.02 10 600? ? ?? ? , B 正确 ;
对于 C,由 频率 分布 直方 图可 知, 众数 的估 计值 为 85,C正确 ;
对于 D,前 三组 频率 之和 为?0.006 0.006 0.028 10 0.4? ? ? ?? ,前 四组 频率 之和 为
0.4 0.04 10 0.8? ? ? ,则 中位 数在?8 0 , 9 0?内,
设学 生评 分的 中位 数的 估计 值为x,则0 . 4 8 0 0 . 0 4 0 . 5? ? ? ?? ?x ,解 得x?82.5,D 错
误.
故选 :D.
【点 睛】
频率 分布 直方 图中 的常 用结 论:( 1)频 率分 布直 方图 中所 有小 长方 形的 面积 之和 为 1;
(2 )频 率分 布直 方图 中最 高长 方形 底边 中点 对应 的横 坐标 是样 本数 据的 众数 ;( 3)平 分
频率 分布 直方 图中 小矩 形的 面积 且垂 直于 横轴 的直 线与 横轴 交点 的横 坐标 是样 本数 据的 中
位数 ;(4)频 率分 布直 方图 中每 个小 长方 形的 面积 与对 应小 长方 形底 边中 点的 横坐 标的 乘
积之 和是 样本 数据 的平 均数 .
7.【答 案】 C
【分 析】
利用 正弦 定理 结合 大边 对大 角定 理可 判断 A 选项 的正 误; 利用 正弦 定理 可判 断 B 选项 的正
误; 利用 余弦 定理 可判 断 C 选项 的正 误; 利用 基本 不等 式、 余弦 定理 结合 三角 形的 面积 公
式可 判断 D 选项 的正 误.
【详 解】
a b
对于 A 选项 ,若A B? ,则a b? ,由 正弦 定理 可得 ? ,所 以,
sin A sinB
sin sinA B? ,A 选项 正确 ;
对于 B 选项 , ?
b As i n 4 s i n 3 0 2? ? ,则b A a bsin ? ? ,所 以,?A B C 有两 解, B 选项
正确 ;
2 2 2
a ?b ?c
对于 C 选项 ,若?A B C 为钝 角三 角形 且C为钝 角, 则cosC ? ?0,可 得
2ab
2 2 2
a b c? ? , C 选项 错误 ;
对于 D 选项 ,由 余弦 定理 与基 本不 等式 可得
2 2 2 2 2
4? ? ? ? ? ? ? ? ? ?a b c b c A b c b c b c b c b c2 co s 2 ,
即bc?4,当 且仅 当b c? ?2时, 等号 成立 ,
1 3
所以 ,S△ABC ? bcsinA? bc? 3,D 选项 正确 .
2 4
故选 :C.
【点 睛】
方法 点睛 :求 三角 形面 积的 最值 是一 种常 见的 类型 ,主 要方 法有 两类 :
(1 )找 到边 与边 之间 的关 系, 利用 基本 不等 式来 求解 ;
(2 )利 用正 弦定 理, 转化 为关 于某 个角 的三 角函 数, 利用 函数 思想 求解 .
8.【答 案】 D
【分 析】
由题 意结 合向 量共 线的 充分 必要 条件 首先 确定m n, 的关 系, 然后 结合 均值 不等 式的 结论 整
理计 算即 可求 得最 终结 果.
【详 解】 ???? ???? ???? ???? ????
由题 意可 知:AP m AB n AC m AB n AE? ? ? ?3 ,
P B E, , 三点 共线 ,则 :m n? ?3 1,据 此有 :
3 1 ? 3 1? 9n m 9n m
? ?? ? ??m?3n??6? ? ?6?2 ? ?12,
m n ?m n? m n m n
1 1
当且 仅当m? ,n ? 时等 号成 立 .
2 6
3 1
综上 可得 : ? 的最 小值 是 12.
m n
本题 选择D选项 .
9.【试 题来 源】 2011 年普 通高 等学 校招 生全 国统 一考 试( 山东 卷)
【答 案】 16
【 解 析 】 因 为 高 校 甲 乙 丙 丁 四 个 专 业 分 别 有150 150 400 300, , , 名 学 生 , 所 以 本 校 共 有 学 生
1000名 , 因 为 用 分 层 抽 样 的 方 法 从 该 校 四 个 专 业 共 抽 取40名 学 生 进 行 调 查 , 所 以 每 个 个
40 1 1
体被 抽到 的概 率是 ? ,因 为丙 专业 有4 0 0人, 所以 要抽 取400? ?16人.
1000 25 25
2
10.【答 案】3
【分 析】
在甲 、乙 、丙 处投 中分 别记 为事 件A,B,C,恰 好投 中两 次为 事件ABC,ABC,
ABC发生 ,由 此利 用相 互独 立事 件概 率乘 法公 式能 求出 结果 .
【详 解】
在甲 、乙 、丙 处投 中分 别记 为事 件A,B,C,
恰好 投中 两次 为事 件ABC,ABC,ABC发生 ,
1 1 1 ? 1? 1 1 7
故恰 好投 中两 次的 概率P? ? ??1? p?? ??1? ?? p?( 1? )? ? p? ,
3 2 3 ? 2? 3 2 18
2
解得p? .
3
2
故答 案为 : .
3
【点 睛】
本题 考查 概率 的求 法, 考查 相互 独立 事件 概率 乘法 公式 等基 础知 识, 考查 运算 求解 能力 ,
是基 础题 .
11.【答 案】 B
【分 析】
利用 方差 公式 可求 得结 果.
【详 解】
6 6
1 2
设原 数据 为a1、a2、a3、a4、a5、a6,则?ai ? ? ?6 4 24, ??ai ?4? ?8
i?1 6 i?1
6 ai ?2?6
加入2和6两个 新数 据后 ,所 得8个数 据的 平均 数为?
i?1 ,
?4
8
6 2 2 2
? ? ? ? ? ?ai ? ? ? ? ?4 2 4 6 4
所得8个数 据的 方差 为 ?
2 i?1 48 4 4? ? .
s ? ? ? 7
8 8
故选 :B.
12.【答 案】?16
【详 解】
以 A 为坐 标原 点, AB 所在 直线 为 x 轴建 系, 则???? ???? ????
F D E G(3, 3), ( 0, 4 ), ( 2, 2 ), (3, 1)?? ?FD EA AG? ? ?
(( 3, 1) ( 2, 2 )) (3, 1) ( 5, 1) (3, 1) 1 6? ? ? ? ? ? ? ? ? ? ?
7
13.8
14. C
?
15. 【答 案 】( 1) ;( 2)2 3.
3
【解 析】
【 分 析 】( 1 ) 在?ABC中 , 由 正 弦 定 理 化 简 得sinA?sin AcosC? 3sinAsinC ?0 , 又
? 1
由sin 0A? ,化 简得sin(C? )? ,即 可求 得C的值 ;
6 2
(2 )在?ABC中, 由余 弦定 理, 列出 关于a方程 ,求 得a b? ?2, 4,再 利用 三角 形的 面
积公 式, 即可 求解 .
【详 解】( 1)由 题意 ,知a?b?ccosA? 3asinC ?0,
由正 弦定 理可 得sinA?sinB?sinCcosA? 3sinAsinC ?0 ,
整理 得sinA?sin(A?C)?sinCcosA? 3sinAsinC ?0,
即sinA?sin AcosC? 3sinAsinC ?0,
?
又因 为A?( 0, )? ,则sin 0A? ,所 以 3sinC?cosC ?2sin(C? )?1,
6
? 1
即sin(C? )? ,
6 2
? ? 5? ? ? ?
又因 为? ?C? ? ,所 以C? ? ,解 得C ? .
6 6 6 6 6 3
2 2 2 2 2
(2 )在?ABC中, 由余 弦定 理可 得c a b ab C a b ab? ? ? ? ? ?2 cos ,
2 2 2 2
因为c?2 3,b a?2 ,所 以1 2 4 2 3? ? ? ?a a a a ,解 得a?2,所 以b a? ?2 4,
1 1 3
则三 角形 的面 积S ? absinC ? ?2?4? ?2 3.
2 2 2
【点 睛】 本题 主要 考查 了正 弦定 理、 余弦 定理 和三 角形 的面 积公 式的 应用 ,其 中在 解有 关
三角 形的 题目 时, 要抓 住题 设条 件和 利用 某个 定理 的信 息, 合理 应用 正弦 定理 和余 弦定 理
李额 方程 求解 是解 答的 关键 ,着 重考 查了 运算 与求 解能 力, 属于 基础 题.
16. 【答 案 】( 1)证 明见 解析 ;( 2)证 明见 解析 .
【解 析】
【 分 析 】( 1 ) 取P D的 中 点N , 连 结MN ,CN , 推 导 出 四 边 形BMNC是 平 行 四 边 形 ,
得到BM CN/ / ,由 线面 平行 的判 定定 理, 即可 证明B M / /平面PCD.
(2 )由 面面 垂直 的性 质定 理可 证A B ?平面PAD,A B DM? ,D M P A? ,得 到
D M ?平面P A B,由 面面 垂直 的判 定定 理, 可证 明平 面B D M ?平面P A B.
【详 解】 证明 :(1)取P D的中 点N ,连 接MN ,CN .
因为M 是P A的中 点,
所以MN 为△PAD的中 位线 ,
1
所以MN// AD.
2
1
又因 为BC// AD,
2
所以MN//BC,
所以 四边 形BMNC为平 行四 边形 ,
所以BM CN/ / .
又B M ? 平面PCD,CN ?平面PCD,
所以B M / /平面PCD.
(2 )因 为平 面P A D ?平面ABCD,且 平面PAD?平面ABCD AD? ,AB AD? ,
AB?平面ABCD,所 以A B ?平面PAD.
∵D M ?平面PAD, ∴A B DM? .
又因 为DP DA? ,M 为P A的中 点, 所以D M P A? ,
∵P A?平面P A B,AB?平面P A B,且PA AB A? ? ,
所以D M ?平面P A B.
又D M ?平面B D M ,
所以 平面B D M ?平面P A B.
【点 睛】 本题 考查 线面 平行 、面 面垂 直的 证明 ,考 查空 间中 线线 、线 面、 面面 间的 位置 关
系等 基础 知识 ,考 查运 算求 解能 力, 是中 档题 .
17.(1 )由频 率分 布直 方图 可知 ,第 四个 矩形 的高 为:
0.1-(0.0 10+0 .020 +0.03 0+0.01 2)=0. 028 ,成 绩不 低于 120 分的 频率 为:
(0.03 0+0.0 28+0. 012) ×10=0.7 ;所 以高 三年 级不 低于 120 分的 人数 为:
0.7×1000 =700 人 .
(2) 由频 率分 布直 方图 知, 成绩 在[140 ,150 ] 的人 数是 6 ,记 女生 为 A ,B,男
生 为 c,d,e,f , 从 这 6 人 中 抽 取 2 人 的 情 况 有 AB , Ac , Ad , Ae , Af , Bc , Bd, Be,
Bf , cd , ce, cf , de , df , ef , 共 15 种 . 其 中 至 少 有 一 名 女 生 的 情 况 有 9 种 , 故 至 少
有一 名女 生的 概率 为 .
18.
(1 )证 明:取A B的中 点F ,连 接DF,交A B1 于点M ,可 知M 为DF的中 点,
连接E M ,易 知四 边形C D M E1 为平 行四 边形 ,所 以C D EM1 / / ,
又C D1 ?平面A BE1 ,EM ?平面A BE1 ,所 以C D1 / /平面A BE1 .
(2 )分 别以C A C B C C, , 1所在 的直 线为x轴、 y轴,z轴建 立如 图所 示的 空间 直角 坐标
系,
可得B C E A( 0, 2, 0), ( 0, 0, 2), ( 0, 0, 1), ( 2, 0, 2)1 1 ,
????? ???? ????
则BC EA EB1 ? ? ? ? ?(0, 2, 2), ( 2, 0, 1), (0, 2, 1)1 ,
?
设平 面A BE1 的法 向量 为n x y z?( , , ),
????
??
n EA? ?1 0 ?2 0x z? ? ?
则?? ???? ,即? ,令x?1,可 得 y z? ? ? ?1, 2,即n? ? ?(1, 1, 2),
?n EB? ?0 ?2 0y z? ?
????? ?
????? ? BC1?n 3
所以cos BC1,n ? ????? ? ?? ,
BC1 ? n 6
3
所以 直线BC1与平 面A BE1 所成 角的 正弦 值为 .
6
(3 )假 设在 棱C C1是存 在一 点P,设C P a a? ? ?, ( 0 2 ),可 得P a( 0, 0, ),
???? ????
由A B(2, 0, 0), (0, 2, 0),可 得P A a P B a? ? ? ?( 2, 0, ), ( 0, 2, ),
??
设平 面P A B的法 向量 为m x y z?( , , )1 1 1 ,
????
??
m PA? ?0 ?2 0x az1? ? ??
则?? ???? ,即? ,令z ?2,可 得x a y a1 1? ?, ,即m a a?( , , 2 ),
?m PB? ?0 ?2 0y az2 ? ?
?
又由 平面A BE1 的一 个法 向量 为n? ? ?(1, 1, 2),所 以
?? ?
?? ? m?n ?4
cos m,n ? ?? ? ?
2 2 ,因 为平 面P A B与平 面A BE1 所成 二面 角为
m ? n a ?a ?4? 6
?
60 ,
4 ? 1 2 10 30
可得 ? ?
2 2 cos60 ,解 得a ? ,此 时a ? ,符 合题 意,
a ?a ?4? 6 2 3 3
? 30 ?
P??0,0, ?
3 ? ?
所以 在棱C C1上存 在一 点 ? ? A BE
,使 得平 面P A B与平 面 1 所成 二面 角为60 .
同课章节目录
