1.2 反比例函数的图象与性质 课件(共39张PPT)
文档属性
| 名称 | 1.2 反比例函数的图象与性质 课件(共39张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 06:40:02 | ||
图片预览







文档简介
第一章 反比例函数
2 反比例函数的图象与性质
知识点一 反比例函数的图象
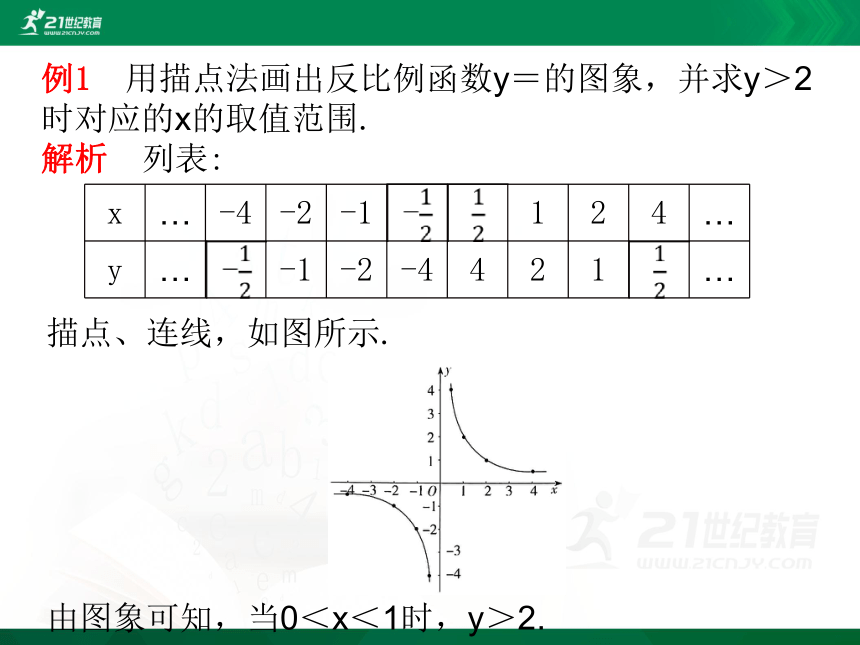
例1 用描点法画出反比例函数y=的图象,并求y>2时对应的x的取值范围.
例1 用描点法画出反比例函数y=的图象,并求y>2时对应的x的取值范围.
解析 列表:
x
…
-4
-2
-1
1
2
4
…
y
…
-1
-2
-4
4
2
1
…
描点、连线,如图所示.
由图象可知,当0<x<1时,y>2.
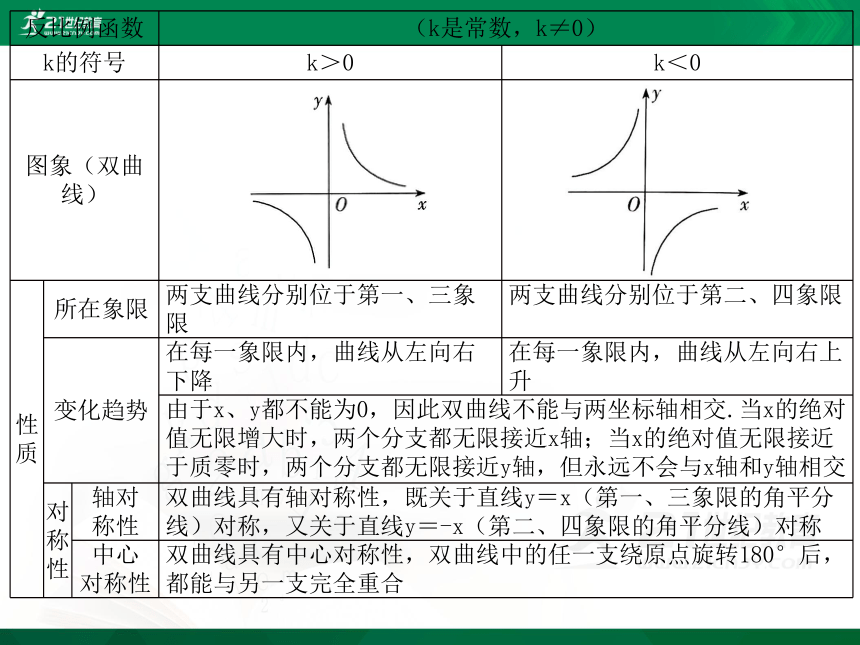
反比例函数
(k是常数,k≠0)
k的符号
k>0
k<0
图象(双曲线)
性质
所在象限
两支曲线分别位于第一、三象限
两支曲线分别位于第二、四象限
变化趋势
在每一象限内,曲线从左向右下降
在每一象限内,曲线从左向右上升
由于x、y都不能为0,因此双曲线不能与两坐标轴相交.当x的绝对值无限增大时,两个分支都无限接近x轴;当x的绝对值无限接近于质零时,两个分支都无限接近y轴,但永远不会与x轴和y轴相交
对称性
轴对
称性
双曲线具有轴对称性,既关于直线y=x(第一、三象限的角平分线)对称,又关于直线y=-x(第二、四象限的角平分线)对称
中心
对称性
双曲线具有中心对称性,双曲线中的任一支绕原点旋转180°后,都能与另一支完全重合
知识点二 反比例函数的性质
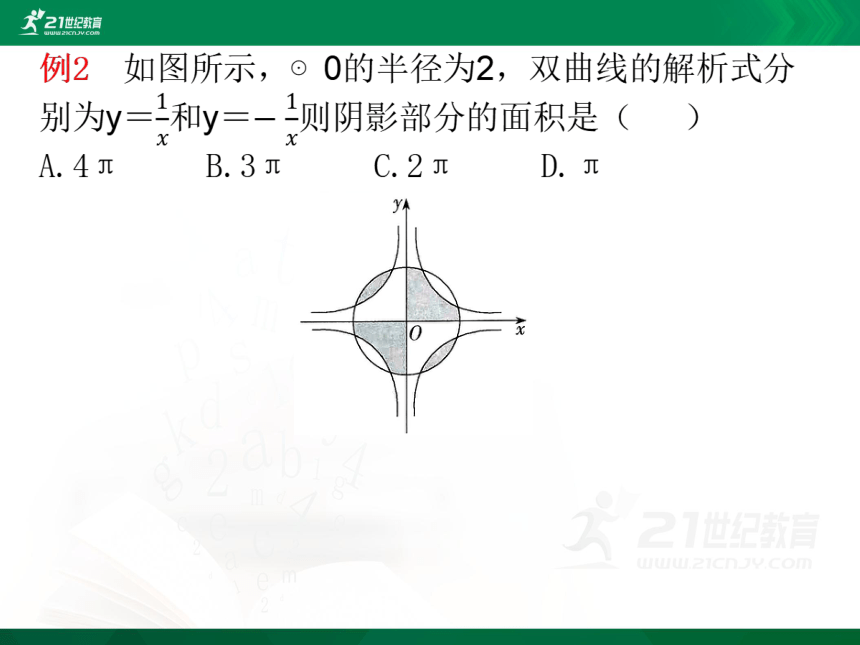
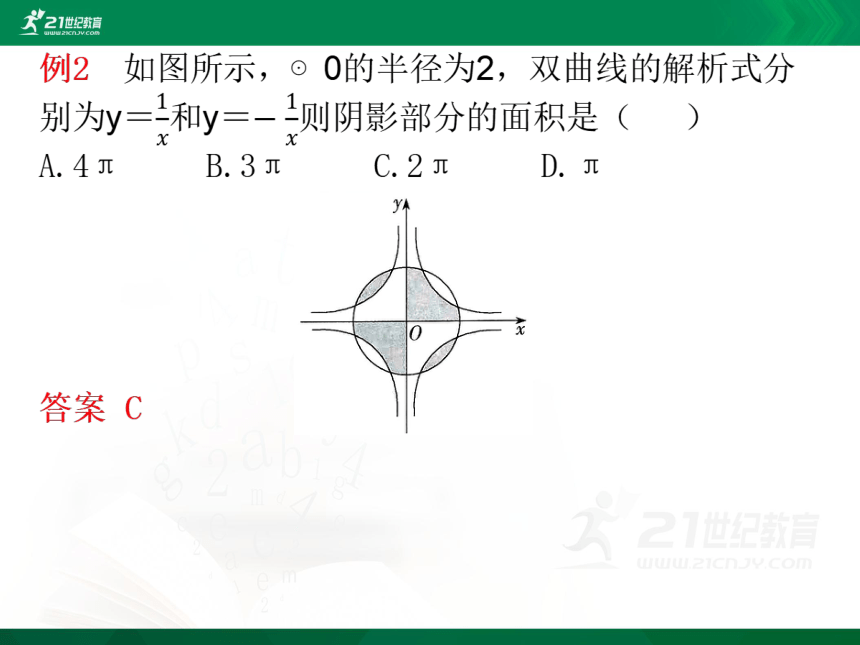
知识点三 反比例函数比例系数的几何意义
知识点三 反比例函数比例系数的几何意义
经典例题
题型一 反比例函数值的大小比较
题型一 反比例函数值的大小比较
题型一 反比例函数值的大小比较
题型一 反比例函数值的大小比较
方法归纳
反比例函数值的大小比较问题,可通过代入特殊值进行判断,但借助图象直观地判断更加简捷.
题型二 一次函数、反比例函数的图象综合判断题
方法归纳
反比例函数与一次函数的表达式中,若含有一个字母,则通常按该字母的正、负两种情况讨论较为简捷;若含有两个字母,则可以根据它们的正、负分四种情况讨论,或是逐个选项进行判断.
题型三 双曲线与几何图形综合题
题型三 双曲线与几何图形综合题
方法技巧
解决此题的方法是利用菱形的对角线互相垂直,添加辅助线,构造相似三角形,利用相似三角形的面积比即为两反比例函数的比例系数的比的绝对值巧解问题.
易错易混
易错点 由面积判断值,忽略符号或分类讨论
由反比例函数比例系数的几何意义可以巧妙求解图形的面积,但反过来,由图形面积判断比例系数k值,要注意若反比例函数的图象位于第二、四象限,则k值为负;若不能确定图象所在象限,则k值有两种情况.
2 反比例函数的图象与性质
知识点一 反比例函数的图象
例1 用描点法画出反比例函数y=的图象,并求y>2时对应的x的取值范围.
例1 用描点法画出反比例函数y=的图象,并求y>2时对应的x的取值范围.
解析 列表:
x
…
-4
-2
-1
1
2
4
…
y
…
-1
-2
-4
4
2
1
…
描点、连线,如图所示.
由图象可知,当0<x<1时,y>2.
反比例函数
(k是常数,k≠0)
k的符号
k>0
k<0
图象(双曲线)
性质
所在象限
两支曲线分别位于第一、三象限
两支曲线分别位于第二、四象限
变化趋势
在每一象限内,曲线从左向右下降
在每一象限内,曲线从左向右上升
由于x、y都不能为0,因此双曲线不能与两坐标轴相交.当x的绝对值无限增大时,两个分支都无限接近x轴;当x的绝对值无限接近于质零时,两个分支都无限接近y轴,但永远不会与x轴和y轴相交
对称性
轴对
称性
双曲线具有轴对称性,既关于直线y=x(第一、三象限的角平分线)对称,又关于直线y=-x(第二、四象限的角平分线)对称
中心
对称性
双曲线具有中心对称性,双曲线中的任一支绕原点旋转180°后,都能与另一支完全重合
知识点二 反比例函数的性质
知识点三 反比例函数比例系数的几何意义
知识点三 反比例函数比例系数的几何意义
经典例题
题型一 反比例函数值的大小比较
题型一 反比例函数值的大小比较
题型一 反比例函数值的大小比较
题型一 反比例函数值的大小比较
方法归纳
反比例函数值的大小比较问题,可通过代入特殊值进行判断,但借助图象直观地判断更加简捷.
题型二 一次函数、反比例函数的图象综合判断题
方法归纳
反比例函数与一次函数的表达式中,若含有一个字母,则通常按该字母的正、负两种情况讨论较为简捷;若含有两个字母,则可以根据它们的正、负分四种情况讨论,或是逐个选项进行判断.
题型三 双曲线与几何图形综合题
题型三 双曲线与几何图形综合题
方法技巧
解决此题的方法是利用菱形的对角线互相垂直,添加辅助线,构造相似三角形,利用相似三角形的面积比即为两反比例函数的比例系数的比的绝对值巧解问题.
易错易混
易错点 由面积判断值,忽略符号或分类讨论
由反比例函数比例系数的几何意义可以巧妙求解图形的面积,但反过来,由图形面积判断比例系数k值,要注意若反比例函数的图象位于第二、四象限,则k值为负;若不能确定图象所在象限,则k值有两种情况.
