2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(word版含解析)
文档属性
| 名称 | 2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 236.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 07:30:19 | ||
图片预览


文档简介
2020-2021学年鲁教五四新版六年级下册数学期末冲刺试题
一.选择题(共12小题,满分36分,每小题3分)
1.以下问题,不适合用普查的是( )
A.了解全班同学每周体育锻炼的时间
B.了解一批灯泡的使用寿命
C.学校招聘教师,对应聘人员面试
D.了解“神舟二号”飞船零部件的状况
2.三条直线l1,l2,l3,若l1∥l3,l2∥l3,则l1与l2的位置关系是( )
A.l1⊥l2
B.l1∥l2
C.l1⊥l2或l1∥l2
D.无法确定
3.能清楚的看出每个项目的具体数量的统计图是( )
A.扇形统计图
B.折线统计图
C.条形统计图
D.以上三种均可
4.要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.每位考生的数学成绩是个体
C.1000名考生是总体
D.100名考生是样本的容量
5.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
6.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等
B.互余或互补
C.互补
D.相等或互补
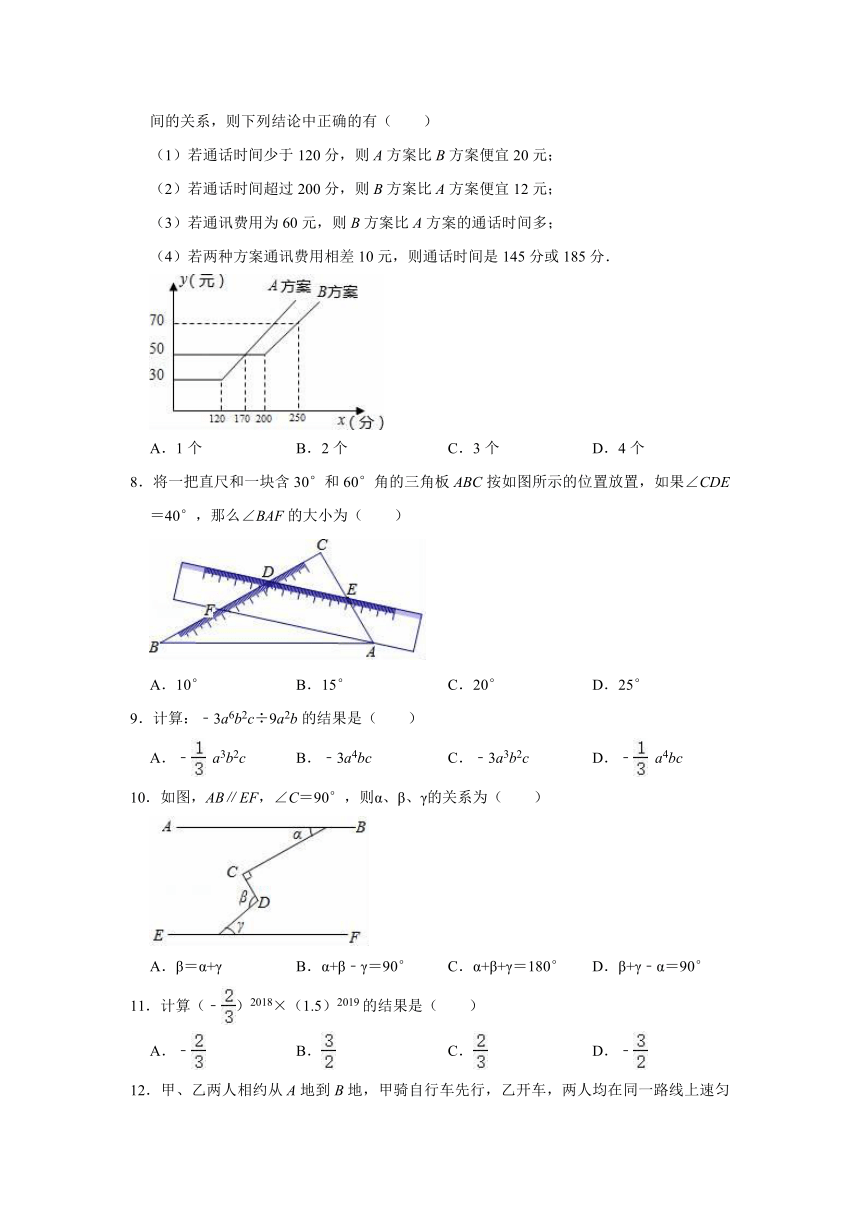
7.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个
B.2个
C.3个
D.4个
8.将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为( )
A.10°
B.15°
C.20°
D.25°
9.计算:﹣3a6b2c÷9a2b的结果是( )
A.﹣
a3b2c
B.﹣3a4bc
C.﹣3a3b2c
D.﹣
a4bc
10.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ
B.α+β﹣γ=90°
C.α+β+γ=180°
D.β+γ﹣α=90°
11.计算(﹣)2018×(1.5)2019的结果是( )
A.﹣
B.
C.
D.﹣
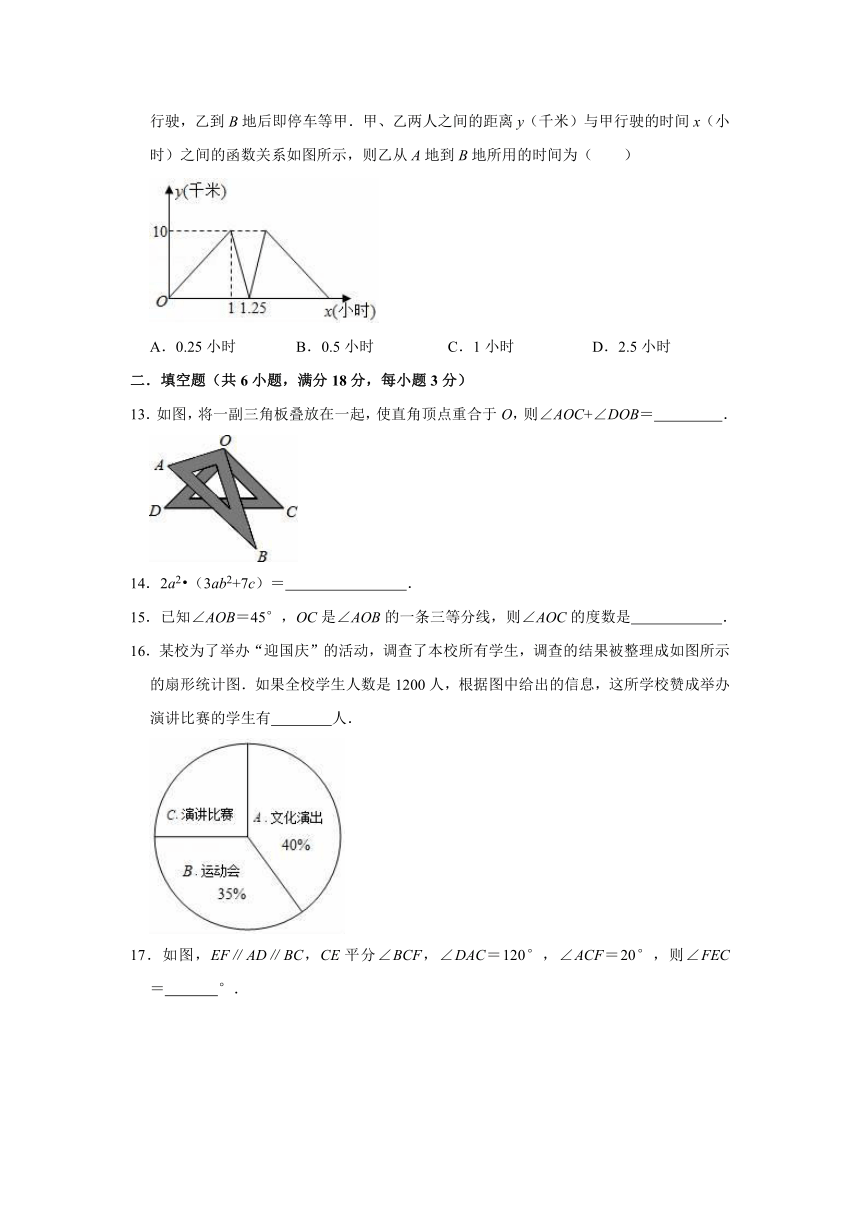
12.甲、乙两人相约从A地到B地,甲骑自行车先行,乙开车,两人均在同一路线上速匀行驶,乙到B地后即停车等甲.甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为( )
A.0.25小时
B.0.5小时
C.1小时
D.2.5小时
二.填空题(共6小题,满分18分,每小题3分)
13.如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=
.
14.2a2?(3ab2+7c)=
.
15.已知∠AOB=45°,OC是∠AOB的一条三等分线,则∠AOC的度数是
.
16.某校为了举办“迎国庆”的活动,调查了本校所有学生,调查的结果被整理成如图所示的扇形统计图.如果全校学生人数是1200人,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有
人.
17.如图,EF∥AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,则∠FEC=
°.
18.如图,这是用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成…按照这样的规律排列下去,则第6个图案中共有
个白子.
三.解答题(共7小题,满分66分)
19.化简:
(1)(a+b)2+(a﹣b)(a+b)﹣2ab;
(2)(a2b﹣2ab2﹣b3)÷b﹣(a﹣b)2.
20.先化简,再求值:3x2y﹣[2x2y﹣x(xy+3)],其中x=﹣,y=2.
21.如图,已知AB∥CD,AE平分∠BAD,DF平分∠ADC,EF交AD于点O,求证∠E=∠F.
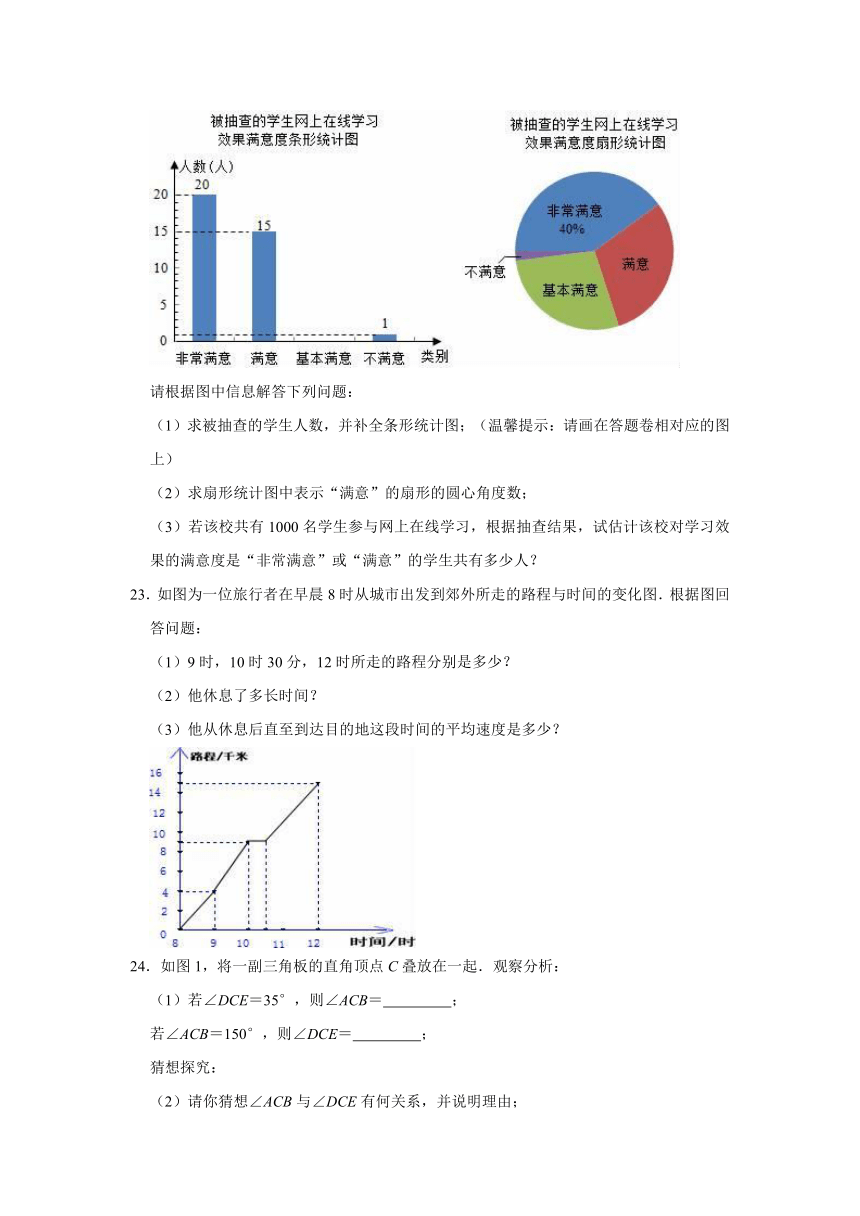
22.为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)
(2)求扇形统计图中表示“满意”的扇形的圆心角度数;
(3)若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?
23.如图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少?
(2)他休息了多长时间?
(3)他从休息后直至到达目的地这段时间的平均速度是多少?
24.如图1,将一副三角板的直角顶点C叠放在一起.观察分析:
(1)若∠DCE=35°,则∠ACB=
;
若∠ACB=150°,则∠DCE=
;
猜想探究:
(2)请你猜想∠ACB与∠DCE有何关系,并说明理由;
拓展应用:
(3)如图2,若将两个同样的三角尺60°锐角的顶点A重合在一起,请你猜想∠DAB与∠CAE有何关系,请说明理由;
(4)如图3,如果把任意两个锐角∠AOB、∠COD的顶点O重合在一起,已知∠AOB=α,∠COD=β(α、β都是锐角),请你直接写出∠AOD与∠BOC的关系.
25.若x满足(9﹣x)(x﹣4)=4,求(9﹣x)2+(x﹣4)2的值.
解:设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面问题:
(1)若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值;
(2)如图,在长方形ABCD中,AB=20,BC=12,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为160平方单位,则图中阴影部分的面积和为多少平方单位?
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、了解全班同学每周体育锻炼的时间,数量不多,全面调查所获数据较为准确,适合普查;
B、了解一批灯泡的使用寿命,具有破坏性,适合抽样调查;
C、学校招聘教师,对应聘人员的面试是事关重大的调查适合普查;
D、对“神舟二号”飞船零部件状况的检查要求精确度高,适宜于普查;
故选:B.
2.解:∵l1∥l3,l2∥l3,
∴l1∥l2.
故选:B.
3.解:条形统计图能清楚地表示出每个项目的具体数目,故C符合题意.
故选:C.
4.解:A、这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B、每位考生的数学成绩是个体,故本选项符合题意;
C、1000名考生的数学成绩是总体,故本选项不合题意;
D、样本的容量是100,故本选项不合题意.
故选:B.
5.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
6.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
7.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当B方案为50元,A方案是40元或者60元时,两种方案通讯费用相差10元,
将yA=40或60代入,得x=145分或195分,故(4)错误;
故选:C.
8.解:由题意知DE∥AF,
∴∠AFD=∠CDE=40°,
∵∠B=30°,
∴∠BAF=∠AFD﹣∠B=40°﹣30°=10°,
故选:A.
9.解:﹣3a6b2c÷9a2b=﹣a4bc.
故选:D.
10.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
11.解:(﹣)2018×(1.5)2019
=()2018×(1.5)2018×1.5
=
=.
故选:B.
12.解:由图像可得:甲骑自行车的速度为10÷1=10千米/小时,乙出发0.25小时追上甲,
设乙速度为x千米/小时,
0.25x=1.25×10,
解得:x=50,
∴乙速度为50千米/小时,
设追上后到达B地的时间是y,
50y﹣10y=10,
解得:y=0.25,
∴乙从A地到B地所用的时间为0.25+0.25=0.5(小时),
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
13.解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,
所以∠AOC+∠BOD=90°+a+90°﹣a=180°.
故答案为:180°.
14.解:原式=6a3b2+14a2c.
故答案为:6a3b2+14a2c.
15.解:当∠AOC=∠AOB时,则∠AOC=×45°=15°,
当∠AOC=∠AOB时,则∠AOC=×45°=30°,
则∠AOC的度数是15°或30°;
故答案为:15°或30°.
16.解:由统计图可得,
这所学校赞成举办演讲比赛的学生有:1200×(1﹣40%﹣35%)=1200×25%=300(人),
故答案为:300.
17.解:∵AD∥BC,
∴∠ACB+∠DAC=180°,
∴∠ACB=180°﹣120°=60°,
∴∠BCF=∠ACB﹣∠ACF=60°﹣20°=40°,
∵CE平分∠BCF,
∴∠BCE=∠BCF=20°,
∵EF∥BC,
∴∠FEC=∠BCE=20°.
故答案为20.
18.解:第1个图案由1个黑子组成,
第2个图案由1个黑子和6个白子组成,
第3个图案由1+3×6﹣6=13个黑子和6个白子组成,
第4个图案由13个黑子和6+4×6﹣6=24个白子组成,
第5个图案由13+5×6﹣6=37个黑子和24个白子组成,
第6个图案由37个黑子和24+6×6﹣6=54个白子组成.
故答案为54.
三.解答题(共7小题,满分66分)
19.解:(1)原式=(a2+2ab+b2)+(a2﹣b2)﹣2ab
=a2+2ab+b2+a2﹣b2﹣2ab
=2a2;
(2)原式=a2﹣2ab﹣b2﹣(a2﹣2ab+b2)
=a2﹣2ab﹣b2﹣a2+2ab﹣b2
=﹣2b2.
20.解:原式=3x2y﹣(2x2y﹣x2y﹣3x)
=3x2y﹣(x2y﹣3x)
=3x2y﹣x2y+3x
=2x2y+3x
当x=,y=2时,
原式=2××2+3×()
=1
=.
21.证明:∵AB∥CD,
∴∠BAD=∠ADC,
∵AE平分∠BAD,DF平分∠ADC,
∴∠EAD=∠BAD,∠FDA=∠ADC,
∴∠EAD=∠FDA,
∴AE∥FD,
∴∠E=∠F.
22.解:(1)抽查的学生数:20÷40%=50(人),
抽查人数中“基本满意”人数:50﹣20﹣15﹣1=14(人),补全的条形统计图如图所示:
(2)360°×=108°,
答:扇形统计图中表示“满意”的扇形的圆心角度数为108°;
(3)1000×(+)=700(人),
答:该校共有1000名学生中“非常满意”或“满意”的约有700人.
23.解:(1)看图可知y值:4km,9km,15km;
(2)根据图象可得,路程没有变化,但时间在增长,故表示该旅行者在休息:10.5﹣10=0.5小时=30分钟;
(3)根据求平均速度的公式可求得
(15﹣9)÷(12﹣10.5)=4km/时.
24.解:(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°﹣35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=150°,
∵∠BCE=90°,
∴∠ACE=150°﹣90°=60°,
∵∠ACD=90°,
∴∠DCE=90°﹣60°=30°,
故答案为:145°,30°;
(2)∠ACB+∠DCE=180°,
理由:∵∠ACE+∠ECD=90°,∠ECD+∠DCB=90°,
∴∠ACE+∠ECD+∠ECD+∠DCB=180°,
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠ECD=180°;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠EAC=120°;
(4)∠AOD+∠BOC=α+β,理由是:
∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC,
=β+∠AOB,
=α+β.
25.解:(1)设5﹣x=a,x﹣2=b,则(5﹣x)(x﹣2)=ab=2,a+b=(5﹣x)+(x﹣2)=3,
∴(5﹣x)2+(x﹣2)2=(a+b)2﹣2ab=32﹣2×2=5;
(2)由题意得:CF=20﹣x,CE=12﹣x,
则长方形CEPF的面积为(20﹣x)(12﹣x)=160平方单位.
阴影部分面积和为:(20﹣x)2+(12﹣x)2,
设20﹣x=a,12﹣x=b,
则(20﹣x)(12﹣x)=ab=160,
∵a﹣b=(20﹣x)﹣(12﹣x)=8,
∴(20﹣x)2+(12﹣x)2=(a﹣b)2+2ab=82+2×160=384.
∴阴影部分面积和为384平方单位.
一.选择题(共12小题,满分36分,每小题3分)
1.以下问题,不适合用普查的是( )
A.了解全班同学每周体育锻炼的时间
B.了解一批灯泡的使用寿命
C.学校招聘教师,对应聘人员面试
D.了解“神舟二号”飞船零部件的状况
2.三条直线l1,l2,l3,若l1∥l3,l2∥l3,则l1与l2的位置关系是( )
A.l1⊥l2
B.l1∥l2
C.l1⊥l2或l1∥l2
D.无法确定
3.能清楚的看出每个项目的具体数量的统计图是( )
A.扇形统计图
B.折线统计图
C.条形统计图
D.以上三种均可
4.要想了解九年级1000名考生的数学成绩,从中抽取了100名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这100名考生是总体的一个样本
B.每位考生的数学成绩是个体
C.1000名考生是总体
D.100名考生是样本的容量
5.下列图形中,线段AD的长表示点A到直线BC距离的是( )
A.
B.
C.
D.
6.如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( )
A.相等
B.互余或互补
C.互补
D.相等或互补
7.如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(分)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.
A.1个
B.2个
C.3个
D.4个
8.将一把直尺和一块含30°和60°角的三角板ABC按如图所示的位置放置,如果∠CDE=40°,那么∠BAF的大小为( )
A.10°
B.15°
C.20°
D.25°
9.计算:﹣3a6b2c÷9a2b的结果是( )
A.﹣
a3b2c
B.﹣3a4bc
C.﹣3a3b2c
D.﹣
a4bc
10.如图,AB∥EF,∠C=90°,则α、β、γ的关系为( )
A.β=α+γ
B.α+β﹣γ=90°
C.α+β+γ=180°
D.β+γ﹣α=90°
11.计算(﹣)2018×(1.5)2019的结果是( )
A.﹣
B.
C.
D.﹣
12.甲、乙两人相约从A地到B地,甲骑自行车先行,乙开车,两人均在同一路线上速匀行驶,乙到B地后即停车等甲.甲、乙两人之间的距离y(千米)与甲行驶的时间x(小时)之间的函数关系如图所示,则乙从A地到B地所用的时间为( )
A.0.25小时
B.0.5小时
C.1小时
D.2.5小时
二.填空题(共6小题,满分18分,每小题3分)
13.如图,将一副三角板叠放在一起,使直角顶点重合于O,则∠AOC+∠DOB=
.
14.2a2?(3ab2+7c)=
.
15.已知∠AOB=45°,OC是∠AOB的一条三等分线,则∠AOC的度数是
.
16.某校为了举办“迎国庆”的活动,调查了本校所有学生,调查的结果被整理成如图所示的扇形统计图.如果全校学生人数是1200人,根据图中给出的信息,这所学校赞成举办演讲比赛的学生有
人.
17.如图,EF∥AD∥BC,CE平分∠BCF,∠DAC=120°,∠ACF=20°,则∠FEC=
°.
18.如图,这是用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成…按照这样的规律排列下去,则第6个图案中共有
个白子.
三.解答题(共7小题,满分66分)
19.化简:
(1)(a+b)2+(a﹣b)(a+b)﹣2ab;
(2)(a2b﹣2ab2﹣b3)÷b﹣(a﹣b)2.
20.先化简,再求值:3x2y﹣[2x2y﹣x(xy+3)],其中x=﹣,y=2.
21.如图,已知AB∥CD,AE平分∠BAD,DF平分∠ADC,EF交AD于点O,求证∠E=∠F.
22.为了解学生对网上在线学习效果的满意度,某校设置了:非常满意、满意、基本满意、不满意四个选项,随机抽查了部分学生,要求每名学生都只选其中的一项,并将抽查结果绘制成如图统计图(不完整).
请根据图中信息解答下列问题:
(1)求被抽查的学生人数,并补全条形统计图;(温馨提示:请画在答题卷相对应的图上)
(2)求扇形统计图中表示“满意”的扇形的圆心角度数;
(3)若该校共有1000名学生参与网上在线学习,根据抽查结果,试估计该校对学习效果的满意度是“非常满意”或“满意”的学生共有多少人?
23.如图为一位旅行者在早晨8时从城市出发到郊外所走的路程与时间的变化图.根据图回答问题:
(1)9时,10时30分,12时所走的路程分别是多少?
(2)他休息了多长时间?
(3)他从休息后直至到达目的地这段时间的平均速度是多少?
24.如图1,将一副三角板的直角顶点C叠放在一起.观察分析:
(1)若∠DCE=35°,则∠ACB=
;
若∠ACB=150°,则∠DCE=
;
猜想探究:
(2)请你猜想∠ACB与∠DCE有何关系,并说明理由;
拓展应用:
(3)如图2,若将两个同样的三角尺60°锐角的顶点A重合在一起,请你猜想∠DAB与∠CAE有何关系,请说明理由;
(4)如图3,如果把任意两个锐角∠AOB、∠COD的顶点O重合在一起,已知∠AOB=α,∠COD=β(α、β都是锐角),请你直接写出∠AOD与∠BOC的关系.
25.若x满足(9﹣x)(x﹣4)=4,求(9﹣x)2+(x﹣4)2的值.
解:设9﹣x=a,x﹣4=b,则(9﹣x)(x﹣4)=ab=4,a+b=(9﹣x)+(x﹣4)=5,
∴(9﹣x)2+(x﹣4)2=a2+b2=(a+b)2﹣2ab=52﹣2×4=17.
请仿照上面的方法求解下面问题:
(1)若x满足(5﹣x)(x﹣2)=2,求(5﹣x)2+(x﹣2)2的值;
(2)如图,在长方形ABCD中,AB=20,BC=12,点E.F是BC、CD上的点,且BE=DF=x,分别以FC、CE为边在长方形ABCD外侧作正方形CFGH和CEMN,若长方形CEPF的面积为160平方单位,则图中阴影部分的面积和为多少平方单位?
参考答案与试题解析
一.选择题(共12小题,满分36分,每小题3分)
1.解:A、了解全班同学每周体育锻炼的时间,数量不多,全面调查所获数据较为准确,适合普查;
B、了解一批灯泡的使用寿命,具有破坏性,适合抽样调查;
C、学校招聘教师,对应聘人员的面试是事关重大的调查适合普查;
D、对“神舟二号”飞船零部件状况的检查要求精确度高,适宜于普查;
故选:B.
2.解:∵l1∥l3,l2∥l3,
∴l1∥l2.
故选:B.
3.解:条形统计图能清楚地表示出每个项目的具体数目,故C符合题意.
故选:C.
4.解:A、这100名考生的数学成绩是总体的一个样本,故本选项不合题意;
B、每位考生的数学成绩是个体,故本选项符合题意;
C、1000名考生的数学成绩是总体,故本选项不合题意;
D、样本的容量是100,故本选项不合题意.
故选:B.
5.解:线段AD的长表示点A到直线BC距离的是图D,
故选:D.
6.解:如图知∠A和∠B的关系是相等或互补.
故选:D.
7.解:依题意得
A:(1)当0≤x≤120,yA=30,
(2)当x>120,yA=30+(x﹣120)×[(50﹣30)÷(170﹣120)]=0.4x﹣18;
B:(1)当0≤x<200,yB=50,
当x>200,yB=50+[(70﹣50)÷(250﹣200)](x﹣200)=0.4x﹣30,
所以当x≤120时,A方案比B方案便宜20元,故(1)正确;
当x≥200时,B方案比A方案便宜12元,故(2)正确;
当y=60时,A:60=0.4x﹣18,∴x=195,
B:60=0.4x﹣30,∴x=225,故(3)正确;
当B方案为50元,A方案是40元或者60元时,两种方案通讯费用相差10元,
将yA=40或60代入,得x=145分或195分,故(4)错误;
故选:C.
8.解:由题意知DE∥AF,
∴∠AFD=∠CDE=40°,
∵∠B=30°,
∴∠BAF=∠AFD﹣∠B=40°﹣30°=10°,
故选:A.
9.解:﹣3a6b2c÷9a2b=﹣a4bc.
故选:D.
10.解:延长DC交AB与G,延长CD交EF于H.
直角△BGC中,∠1=90°﹣α;
△EHD中,∠2=β﹣γ,
∵AB∥EF,
∴∠1=∠2,
∴90°﹣α=β﹣γ,
即α+β﹣γ=90°.
故选:B.
11.解:(﹣)2018×(1.5)2019
=()2018×(1.5)2018×1.5
=
=.
故选:B.
12.解:由图像可得:甲骑自行车的速度为10÷1=10千米/小时,乙出发0.25小时追上甲,
设乙速度为x千米/小时,
0.25x=1.25×10,
解得:x=50,
∴乙速度为50千米/小时,
设追上后到达B地的时间是y,
50y﹣10y=10,
解得:y=0.25,
∴乙从A地到B地所用的时间为0.25+0.25=0.5(小时),
故选:B.
二.填空题(共6小题,满分18分,每小题3分)
13.解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,
所以∠AOC+∠BOD=90°+a+90°﹣a=180°.
故答案为:180°.
14.解:原式=6a3b2+14a2c.
故答案为:6a3b2+14a2c.
15.解:当∠AOC=∠AOB时,则∠AOC=×45°=15°,
当∠AOC=∠AOB时,则∠AOC=×45°=30°,
则∠AOC的度数是15°或30°;
故答案为:15°或30°.
16.解:由统计图可得,
这所学校赞成举办演讲比赛的学生有:1200×(1﹣40%﹣35%)=1200×25%=300(人),
故答案为:300.
17.解:∵AD∥BC,
∴∠ACB+∠DAC=180°,
∴∠ACB=180°﹣120°=60°,
∴∠BCF=∠ACB﹣∠ACF=60°﹣20°=40°,
∵CE平分∠BCF,
∴∠BCE=∠BCF=20°,
∵EF∥BC,
∴∠FEC=∠BCE=20°.
故答案为20.
18.解:第1个图案由1个黑子组成,
第2个图案由1个黑子和6个白子组成,
第3个图案由1+3×6﹣6=13个黑子和6个白子组成,
第4个图案由13个黑子和6+4×6﹣6=24个白子组成,
第5个图案由13+5×6﹣6=37个黑子和24个白子组成,
第6个图案由37个黑子和24+6×6﹣6=54个白子组成.
故答案为54.
三.解答题(共7小题,满分66分)
19.解:(1)原式=(a2+2ab+b2)+(a2﹣b2)﹣2ab
=a2+2ab+b2+a2﹣b2﹣2ab
=2a2;
(2)原式=a2﹣2ab﹣b2﹣(a2﹣2ab+b2)
=a2﹣2ab﹣b2﹣a2+2ab﹣b2
=﹣2b2.
20.解:原式=3x2y﹣(2x2y﹣x2y﹣3x)
=3x2y﹣(x2y﹣3x)
=3x2y﹣x2y+3x
=2x2y+3x
当x=,y=2时,
原式=2××2+3×()
=1
=.
21.证明:∵AB∥CD,
∴∠BAD=∠ADC,
∵AE平分∠BAD,DF平分∠ADC,
∴∠EAD=∠BAD,∠FDA=∠ADC,
∴∠EAD=∠FDA,
∴AE∥FD,
∴∠E=∠F.
22.解:(1)抽查的学生数:20÷40%=50(人),
抽查人数中“基本满意”人数:50﹣20﹣15﹣1=14(人),补全的条形统计图如图所示:
(2)360°×=108°,
答:扇形统计图中表示“满意”的扇形的圆心角度数为108°;
(3)1000×(+)=700(人),
答:该校共有1000名学生中“非常满意”或“满意”的约有700人.
23.解:(1)看图可知y值:4km,9km,15km;
(2)根据图象可得,路程没有变化,但时间在增长,故表示该旅行者在休息:10.5﹣10=0.5小时=30分钟;
(3)根据求平均速度的公式可求得
(15﹣9)÷(12﹣10.5)=4km/时.
24.解:(1)若∠DCE=35°,
∵∠ACD=90°,∠DCE=35°,
∴∠ACE=90°﹣35°=55°,
∵∠BCE=90°,
∴∠ACB=∠ACE+∠BCE=55°+90°=145°;
若∠ACB=150°,
∵∠BCE=90°,
∴∠ACE=150°﹣90°=60°,
∵∠ACD=90°,
∴∠DCE=90°﹣60°=30°,
故答案为:145°,30°;
(2)∠ACB+∠DCE=180°,
理由:∵∠ACE+∠ECD=90°,∠ECD+∠DCB=90°,
∴∠ACE+∠ECD+∠ECD+∠DCB=180°,
∵∠ACE+∠ECD+∠DCB=∠ACB,
∴∠ACB+∠ECD=180°;
(3)∠DAB+∠EAC=120°,
理由:∵∠DAE+∠EAC=60°,∠EAC+∠CAB=60°,
∴∠DAE+∠EAC+∠EAC+∠CAB=120°,
∵∠DAE+∠EAC+∠CAB=∠DAB,
∴∠DAB+∠EAC=120°;
(4)∠AOD+∠BOC=α+β,理由是:
∵∠AOD=∠DOC+∠COA=β+∠COA,
∴∠AOD+∠BOC=β+∠COA+∠BOC,
=β+∠AOB,
=α+β.
25.解:(1)设5﹣x=a,x﹣2=b,则(5﹣x)(x﹣2)=ab=2,a+b=(5﹣x)+(x﹣2)=3,
∴(5﹣x)2+(x﹣2)2=(a+b)2﹣2ab=32﹣2×2=5;
(2)由题意得:CF=20﹣x,CE=12﹣x,
则长方形CEPF的面积为(20﹣x)(12﹣x)=160平方单位.
阴影部分面积和为:(20﹣x)2+(12﹣x)2,
设20﹣x=a,12﹣x=b,
则(20﹣x)(12﹣x)=ab=160,
∵a﹣b=(20﹣x)﹣(12﹣x)=8,
∴(20﹣x)2+(12﹣x)2=(a﹣b)2+2ab=82+2×160=384.
∴阴影部分面积和为384平方单位.
同课章节目录
