1.3 反比例函数的应用 同步练习(含答案)
文档属性
| 名称 | 1.3 反比例函数的应用 同步练习(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 06:41:12 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第一章 反比例函数
3 反比例函数分应用
知识能力全练
知识点一 反比例函数的实际应用
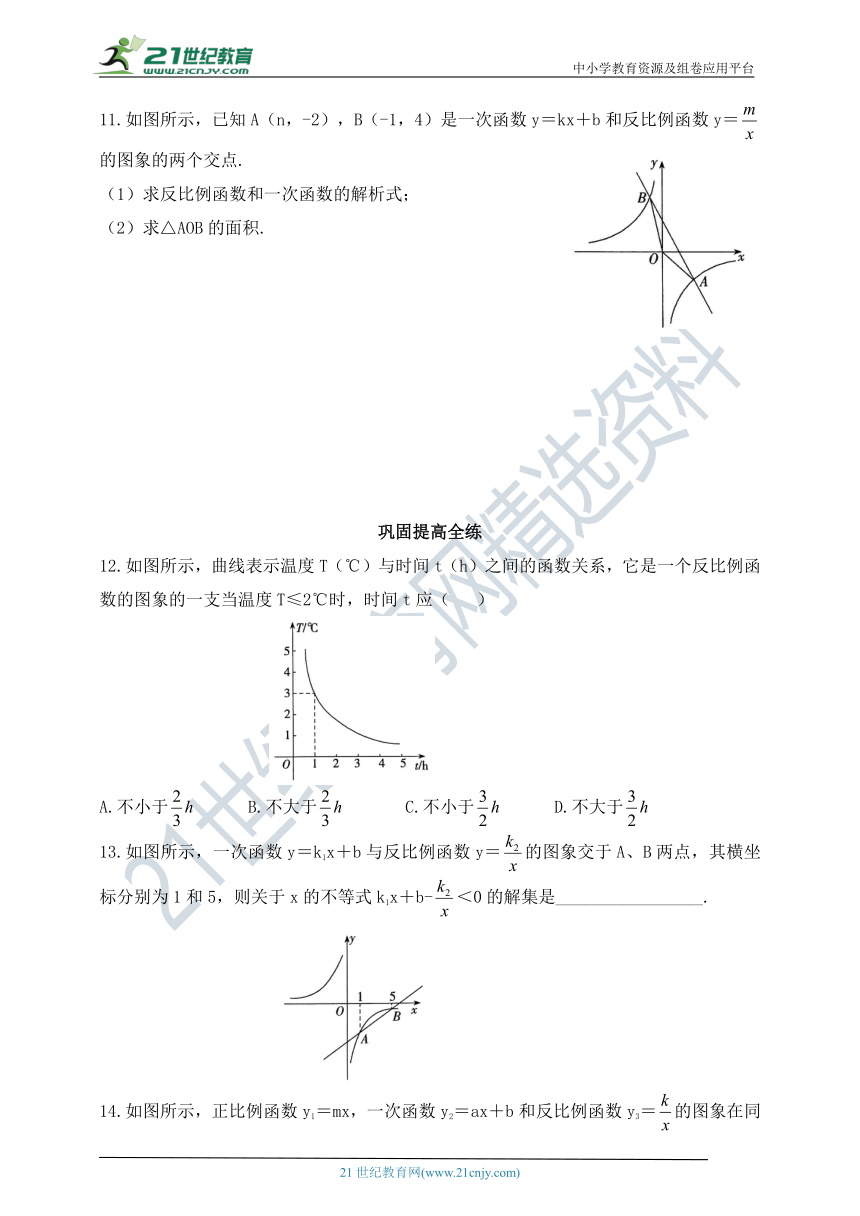
1.已知电压U、电流I、电阻R三者之间的关系式为U=IR(或者),实际生活中,由于给定已知量不同,因此会有不同的可能图象,图象不可能是( )
2.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
3.某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,则当气球内气体体积V(m3)的范围是0.8<V<2时,气体的压强P(kPa)的范围( )
4.小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求y与x之间的函数关系式;
(2)当x的值为6,8,10时,对应的函数值分别为y1,y2,y3,比较(y1-y2)与(y2-y3)的大小:y1-y2_______y2-y3.
5.某家居专营店在网上销售一款wifi万年历电子钟,电子钟每件进价为100元,在销售中发现,该电子钟的日销售量y(块)是销售价x(元/块)的反比例函数,且当销售价定为180元/块时,每日可销售20块.
(1)求y与x之间的函数关系式;
(2)若该家居专营店的日销售利润不低于2000元(运输成本及其他成本忽略不计),则该款电子钟的销售价至少为多少?
6.小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中水温y(℃)与开机时间x(分)成反比例关系).当水温降至20℃时饮水机又自动开始加热,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在给饮水机通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内水的温度约为多少摄氏度.
知识点二 反比例函数与一次函数的综合
7.如图所示,函数y1=x+1与函数y2=的图象相交于点M(1,m),N(-2,n)若y1>y2,则x的取值范围是( )
A.x<-2或0<x<1 B.x<-2或x>1
C.-2<x<0或0<x<1 D.-2<x<0或x>1
8.若正比例函数y=2x的图象与某反比例函数的图象有一个交点的纵坐标是2,则该反比例函数的解析式为____________.
9.已知函数y=与y=2x+1的图象的一个交点为P(m,n),则代数式的值为____________.
10.如图所示,一直线经过原点O且与反比例函数y=(k>0)的图象相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC的面积为8,则k=___________.
11.如图所示,已知A(n,-2),B(-1,4)是一次函数y=kx+b和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
巩固提高全练
12.如图所示,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支当温度T≤2℃时,时间t应( )
A.不小于 B.不大于 C.不小于 D.不大于
13.如图所示,一次函数y=k1x+b与反比例函数y=的图象交于A、B两点,其横坐标分别为1和5,则关于x的不等式k1x+b-<0的解集是_________________.
14.如图所示,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3=的图象在同一直角坐标系中,若y3>y1>y2,则自变量x的取值范围是( )
A.x<-1 B.-0.5<x<0或x>1 C.0<x<1 D.x<-1或0<x<1
15.如图所示,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是2.
(1)求m、n的值;
(2)求直线AC的解析式.
16.如图所示,已知次函数y=kx+b的图象与反比例函数y=的图象交于点A(3,a),点B(14-2a,2).
(1)求反比例函数的表达式;
(2)若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,求△ACD的面积.
17.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19 min;完成2间办公室和1间教室的药物喷洒要11 min.
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算
说明.
18.汛期到来,山洪暴发.下表记录了某水库20 h内水位的变化情况,其中x表示时间(单位:h),y表示水位高度(单位:m),当x=8(h)时,达到警戒水位,开始开闸放水.
x/h 0 2 4 6 8 10 12 14 16 18 20
y/h 14 15 16 17 18 14.4 12 10.3 9 8 7.2
(1)在给出的平面直角坐标系中(如图所示),根据表格中的数据描出相应的点;
(2)请分别求出开闸放水前和放水后最符合表中数据的函数解析式;
(3)据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到6m.
19.如图所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二,四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n>中x的取值范围;
(3)在y轴上取点P,使PB-PA取得最大值时,求出点P的坐标.
20.为了探索函数y=x+(x>0)的图象与性质,我们参照学习函数的过程与方法.
列表:
x …
1 2 3 4 5 …
y …
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图1①所示:
(1)如图①,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;
(2)已知点(x1,y1),(x2,y2)在函数图象上,结合表格和函数图象,回答下列问题(填“>”“=”或“<”):
若0<x1<x2≤1,则y1_________y2;
若1<x1<x2,则y1__________y2;
若x1·x2=1,则y1__________y2.
(3)某农户要建造一个图②所示的长方体形无盖水池,其底面积为1平方米,深为1米已知底面造价为1千元/平方米,侧面造价为0.5千元/平方米.设水池底面一边的长为x米,水池总造价为y千元.
①请写出y与x的函数关系式;
②若该农户预算不超过3.5千元,则水池底面边的长x应控制在什么范围内?
参考答案
1.A 2.B 4. 48<P<120
4.解析 (1)设y与x之间的函数关系式为y=(k≠0),
把(3,400)代入,得400=,解得k=1200.
∴y与x之间的函数关系式为y=.
(2)把x=6.8.10分别代入y=,得
y1==200,y2==150,y3==120.
∵y1-y2=200-150=50,y2-y3=150-120=30.50>30,∴y1-y2>y2-y3.
故填 >
5.解析 (1)设y与x之间的函数关系式为y=(k≠0),
∵当销售价定为180元/块时,每日可销售20块,∴20=.解得k=3600.
∴y与x之间的函数关系式为y=.
(2)设日销售利润不低于2000元时,该款电子钟的销售价为a元/块,a>0,根据题意,得(a-100)·≥2000.解得a≥225.
∴若日销售利润不低于2000元,则该款子钟的销售价至少为225元.
6.解析(1)当0≤x≤8时,设水温y(℃)与开机时间x(分)的函数关系式为y=kx+b(k≠0),
依据题意,得,解得.
∴所求函数解析式为y=10x+20.
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为y=(m≠0),
依据题意,得100=,即m=800,故y=,
当y=20时,20=,解得t=40.
(3)45-40=5<8,当x=5时,y=10x+20=10×5+20=70.
答:小明散步45分钟回到家时,饮水机内水的温度约为70℃.
D 8. 9. 10. 8
11.解析(1):A(n,-2),B(-1,4)是一次数y=kx+b的图象与反比例函数y=的图象的两个交点,∴4=,m=-4.∴y=-.
∴-2=-,∴n=2.∴点A的坐标是(2,-2).
∴,解得.∴一次函数解析式为y=-2x+2.
即反比例函数的解析式为y=-,一次函数的解析式为y=-2x+2.
(2)设直线与y轴的交点为C,则C点坐标为(0,2).
∴S△A0B=S△A0C+S△BOC=×2×2+×2×1=3.
12.C 13.x<0或1<x<5 14.D
15.解析 (1)∵直线y=mx与双曲线y=相交于A(-2,a)、B两点,
∴点A与点B关于原点中心对称.
∴点B的坐标为(2,-a),点C的坐标为(2,0).
∵S△AOC=2,∴×2×a=2,解得a=2.∴A的坐标为(-2,2).
把A(-2,2)代入y=mx和y=,得-2m=2,2=,解得m=-1,n=-4.
(2)设直线AC的解析式为y=kx+b(k≠0),
∵直线AC经过A(-2,2),C(2,0),∴,解得.
∴直线AC的解析式为y=-x+1.
16.解析(1)∵点A(3,a),点B(14-2a,2)在反比例函数y=的图象上,
∴3×a=(14-2a)×2.解得a=4.∴k=3×4=12.
故反比例函数的表达式为y=.
(2)∵a=4,∴点A,B的坐标分别为(3,4),(6,2).
∵点A,B在一次函数y=kx+b的图象上,
∴,解得.故一次函数的表达式为y=-x+6.
当x=0时,y=6,故点C的坐标为(0,6),∴OC=6.
∵点D为点C关于原点O的对称点,CD=20C=12.
∴△ACD的面积=×CD·xA=×12×3=18.
17.解析(1)设完成一间办公室和一间教室药物喷洒各要a min和b min,
则,解得.
故校医完成一间办公室和一间教室的药物洒各要3 min和5 min.
(2)一间教室的药物喷洒时间为5 min则喷洒11间教室需要55 min,
当x=5时,y=2x=10,故点A的坐标为(5,10).
设反比例函数表达式为y=(k≠0),将点A的坐标代入上式,
得10=,解得k=50.故反比例函数表达式为y=.
当x=55时,y=<1,故一班学生能安全进入教室.
18.解析(1)在平面直角坐标系中,根据表格中的数据描出相应的点,如图所示.
(2)观察图象当0≤x≤8时,y与x是一次函数关系:设y=kx+b(k≠0),把(0,14),(8,18)代入得,解得.所以y与x的关系式为y=x+14.
因此放水前y与x的关系式为y=x+14(0≤x<8).
通过观察数据发现:8×18=10×14.4=12×1216×9=18×8=20×7.2=144.
因此放水后y与x的关系符合反比例函数,关系式为y=(x≥8).
所以开闸放水前和放水后最符合表中数据的函数解析式为y=x+4(0≤x<8)和y=(x≥8).
(3)当y=6时,6=,解得x=24,因此预计24h水位达到6 m.
19.解析 (1)∵△AOC的面积为4,∴.
解得k=-8或k=8(不符合题意,舍去).
∴反比例函数的关系式为y=-.
把点A(-2,a)和点B(b,-1)代入y=-,得a=4,b=8.
(2)不等式mx+n>的解集为x<-2或0<x<8.
(3)设点A(-2,4)关于y轴的对称点为A′,则A′的坐标为(2,4).
则直线A′B与y轴的交点即为所求的点P.
设直线AB的关系式为y=cx+d(c≠0),则有,解得.
∴直线AB的关系式为y=-x+.
∵直线y=-x+与y轴的交点坐标为(0,),∴点P的坐标为(0,).
20.解析 (1)函数图象如图所示.
(2)若0<x1<x2≤1,则y1>y2;若1<x1<x2,则y1<y2;若x1·x2=1,则y1=y2,
故填>;<;=.
(3)①由题意,y=1+(2x+)×0.5=1+x+(x>0).
②当y=3.5时,1+x+=3.5,解得x1=,x2=2.
∴当y≤3.5时,≤x≤2.
∴水池底面一边的长x应控制在,≤x≤2的范围内.
_21?????????è?????(www.21cnjy.com)_
第一章 反比例函数
3 反比例函数分应用
知识能力全练
知识点一 反比例函数的实际应用
1.已知电压U、电流I、电阻R三者之间的关系式为U=IR(或者),实际生活中,由于给定已知量不同,因此会有不同的可能图象,图象不可能是( )
2.公元前3世纪,古希腊科学家阿基米德发现了杠杆平衡,后来人们把它归纳为“杠杆原理”,即:阻力×阻力臂=动力×动力臂.小伟欲用撬棍撬动一块石头,已知阻力和阻力臂分别是1200N和0.5m,则动力F(单位:N)关于动力臂(单位:m)的函数解析式正确的是( )
A.F= B.F= C.F= D.F=
3.某气球内充满了一定质量的气体,当温度不变时,气球内气体的压强P(kPa)是气体体积V(m3)的反比例函数,其图象如图所示,则当气球内气体体积V(m3)的范围是0.8<V<2时,气体的压强P(kPa)的范围( )
4.小明同学训练某种运算技能,每次训练完成相同数量的题目,各次训练题目难度相当当训练次数不超过15次时,完成一次训练所需要的时间y(单位:秒)与训练次数x(单位:次)之间满足如图所示的反比例函数关系.完成第3次训练所需时间为400秒.
(1)求y与x之间的函数关系式;
(2)当x的值为6,8,10时,对应的函数值分别为y1,y2,y3,比较(y1-y2)与(y2-y3)的大小:y1-y2_______y2-y3.
5.某家居专营店在网上销售一款wifi万年历电子钟,电子钟每件进价为100元,在销售中发现,该电子钟的日销售量y(块)是销售价x(元/块)的反比例函数,且当销售价定为180元/块时,每日可销售20块.
(1)求y与x之间的函数关系式;
(2)若该家居专营店的日销售利润不低于2000元(运输成本及其他成本忽略不计),则该款电子钟的销售价至少为多少?
6.小明家饮水机中原有水的温度为20℃,通电开机后,饮水机自动开始加热(此过程中水温y(℃)与开机时间x(分)满足一次函数关系),当加热到100℃时自动停止加热,随后水温开始下降(此过程中水温y(℃)与开机时间x(分)成反比例关系).当水温降至20℃时饮水机又自动开始加热,重复上述程序(如图所示),根据图中提供的信息,解答下列问题:
(1)当0≤x≤8时,求水温y(℃)与开机时间x(分)的函数关系式;
(2)求图中t的值;
(3)若小明在给饮水机通电开机后即外出散步,请你预测小明散步45分钟回到家时,饮水机内水的温度约为多少摄氏度.
知识点二 反比例函数与一次函数的综合
7.如图所示,函数y1=x+1与函数y2=的图象相交于点M(1,m),N(-2,n)若y1>y2,则x的取值范围是( )
A.x<-2或0<x<1 B.x<-2或x>1
C.-2<x<0或0<x<1 D.-2<x<0或x>1
8.若正比例函数y=2x的图象与某反比例函数的图象有一个交点的纵坐标是2,则该反比例函数的解析式为____________.
9.已知函数y=与y=2x+1的图象的一个交点为P(m,n),则代数式的值为____________.
10.如图所示,一直线经过原点O且与反比例函数y=(k>0)的图象相交于点A、点B,过点A作AC⊥y轴,垂足为C,连接BC.若△ABC的面积为8,则k=___________.
11.如图所示,已知A(n,-2),B(-1,4)是一次函数y=kx+b和反比例函数y=的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积.
巩固提高全练
12.如图所示,曲线表示温度T(℃)与时间t(h)之间的函数关系,它是一个反比例函数的图象的一支当温度T≤2℃时,时间t应( )
A.不小于 B.不大于 C.不小于 D.不大于
13.如图所示,一次函数y=k1x+b与反比例函数y=的图象交于A、B两点,其横坐标分别为1和5,则关于x的不等式k1x+b-<0的解集是_________________.
14.如图所示,正比例函数y1=mx,一次函数y2=ax+b和反比例函数y3=的图象在同一直角坐标系中,若y3>y1>y2,则自变量x的取值范围是( )
A.x<-1 B.-0.5<x<0或x>1 C.0<x<1 D.x<-1或0<x<1
15.如图所示,在平面直角坐标系中,直线y=mx与双曲线y=相交于A(-2,a)、B两点,BC⊥x轴,垂足为C,△AOC的面积是2.
(1)求m、n的值;
(2)求直线AC的解析式.
16.如图所示,已知次函数y=kx+b的图象与反比例函数y=的图象交于点A(3,a),点B(14-2a,2).
(1)求反比例函数的表达式;
(2)若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,求△ACD的面积.
17.为了做好校园疫情防控工作,校医每天早上对全校办公室和教室进行药物喷洒消毒,她完成3间办公室和2间教室的药物喷洒要19 min;完成2间办公室和1间教室的药物喷洒要11 min.
(1)校医完成一间办公室和一间教室的药物喷洒各要多少时间?
(2)消毒药物在一间教室内空气中的浓度y(单位:mg/m3)与时间x(单位:min)的函数关系如图所示:校医进行药物喷洒时y与x的函数关系式为y=2x,药物喷洒完成后y与x成反比例函数关系,两个函数图象的交点为A(m,n).当教室空气中的药物浓度不高于1mg/m3时,对人体健康无危害,校医依次对一班至十一班教室(共11间)进行药物喷洒消毒,当她把最后一间教室药物喷洒完成后,一班学生能否进入教室?请通过计算
说明.
18.汛期到来,山洪暴发.下表记录了某水库20 h内水位的变化情况,其中x表示时间(单位:h),y表示水位高度(单位:m),当x=8(h)时,达到警戒水位,开始开闸放水.
x/h 0 2 4 6 8 10 12 14 16 18 20
y/h 14 15 16 17 18 14.4 12 10.3 9 8 7.2
(1)在给出的平面直角坐标系中(如图所示),根据表格中的数据描出相应的点;
(2)请分别求出开闸放水前和放水后最符合表中数据的函数解析式;
(3)据估计,开闸放水后,水位的这种变化规律还会持续一段时间,预测何时水位达到6m.
19.如图所示,一次函数y=mx+n(m≠0)的图象与反比例函数y=(k≠0)的图象交于第二,四象限的点A(-2,a)和点B(b,-1),过A点作x轴的垂线,垂足为点C,△AOC的面积为4.
(1)分别求出a和b的值;
(2)结合图象直接写出mx+n>中x的取值范围;
(3)在y轴上取点P,使PB-PA取得最大值时,求出点P的坐标.
20.为了探索函数y=x+(x>0)的图象与性质,我们参照学习函数的过程与方法.
列表:
x …
1 2 3 4 5 …
y …
2
…
描点:在平面直角坐标系中,以自变量x的取值为横坐标,以相应的函数值y为纵坐标,描出相应的点,如图1①所示:
(1)如图①,观察所描出点的分布,用一条光滑曲线将点顺次连接起来,作出函数图象;
(2)已知点(x1,y1),(x2,y2)在函数图象上,结合表格和函数图象,回答下列问题(填“>”“=”或“<”):
若0<x1<x2≤1,则y1_________y2;
若1<x1<x2,则y1__________y2;
若x1·x2=1,则y1__________y2.
(3)某农户要建造一个图②所示的长方体形无盖水池,其底面积为1平方米,深为1米已知底面造价为1千元/平方米,侧面造价为0.5千元/平方米.设水池底面一边的长为x米,水池总造价为y千元.
①请写出y与x的函数关系式;
②若该农户预算不超过3.5千元,则水池底面边的长x应控制在什么范围内?
参考答案
1.A 2.B 4. 48<P<120
4.解析 (1)设y与x之间的函数关系式为y=(k≠0),
把(3,400)代入,得400=,解得k=1200.
∴y与x之间的函数关系式为y=.
(2)把x=6.8.10分别代入y=,得
y1==200,y2==150,y3==120.
∵y1-y2=200-150=50,y2-y3=150-120=30.50>30,∴y1-y2>y2-y3.
故填 >
5.解析 (1)设y与x之间的函数关系式为y=(k≠0),
∵当销售价定为180元/块时,每日可销售20块,∴20=.解得k=3600.
∴y与x之间的函数关系式为y=.
(2)设日销售利润不低于2000元时,该款电子钟的销售价为a元/块,a>0,根据题意,得(a-100)·≥2000.解得a≥225.
∴若日销售利润不低于2000元,则该款子钟的销售价至少为225元.
6.解析(1)当0≤x≤8时,设水温y(℃)与开机时间x(分)的函数关系式为y=kx+b(k≠0),
依据题意,得,解得.
∴所求函数解析式为y=10x+20.
(2)在水温下降过程中,设水温y(℃)与开机时间x(分)的函数关系式为y=(m≠0),
依据题意,得100=,即m=800,故y=,
当y=20时,20=,解得t=40.
(3)45-40=5<8,当x=5时,y=10x+20=10×5+20=70.
答:小明散步45分钟回到家时,饮水机内水的温度约为70℃.
D 8. 9. 10. 8
11.解析(1):A(n,-2),B(-1,4)是一次数y=kx+b的图象与反比例函数y=的图象的两个交点,∴4=,m=-4.∴y=-.
∴-2=-,∴n=2.∴点A的坐标是(2,-2).
∴,解得.∴一次函数解析式为y=-2x+2.
即反比例函数的解析式为y=-,一次函数的解析式为y=-2x+2.
(2)设直线与y轴的交点为C,则C点坐标为(0,2).
∴S△A0B=S△A0C+S△BOC=×2×2+×2×1=3.
12.C 13.x<0或1<x<5 14.D
15.解析 (1)∵直线y=mx与双曲线y=相交于A(-2,a)、B两点,
∴点A与点B关于原点中心对称.
∴点B的坐标为(2,-a),点C的坐标为(2,0).
∵S△AOC=2,∴×2×a=2,解得a=2.∴A的坐标为(-2,2).
把A(-2,2)代入y=mx和y=,得-2m=2,2=,解得m=-1,n=-4.
(2)设直线AC的解析式为y=kx+b(k≠0),
∵直线AC经过A(-2,2),C(2,0),∴,解得.
∴直线AC的解析式为y=-x+1.
16.解析(1)∵点A(3,a),点B(14-2a,2)在反比例函数y=的图象上,
∴3×a=(14-2a)×2.解得a=4.∴k=3×4=12.
故反比例函数的表达式为y=.
(2)∵a=4,∴点A,B的坐标分别为(3,4),(6,2).
∵点A,B在一次函数y=kx+b的图象上,
∴,解得.故一次函数的表达式为y=-x+6.
当x=0时,y=6,故点C的坐标为(0,6),∴OC=6.
∵点D为点C关于原点O的对称点,CD=20C=12.
∴△ACD的面积=×CD·xA=×12×3=18.
17.解析(1)设完成一间办公室和一间教室药物喷洒各要a min和b min,
则,解得.
故校医完成一间办公室和一间教室的药物洒各要3 min和5 min.
(2)一间教室的药物喷洒时间为5 min则喷洒11间教室需要55 min,
当x=5时,y=2x=10,故点A的坐标为(5,10).
设反比例函数表达式为y=(k≠0),将点A的坐标代入上式,
得10=,解得k=50.故反比例函数表达式为y=.
当x=55时,y=<1,故一班学生能安全进入教室.
18.解析(1)在平面直角坐标系中,根据表格中的数据描出相应的点,如图所示.
(2)观察图象当0≤x≤8时,y与x是一次函数关系:设y=kx+b(k≠0),把(0,14),(8,18)代入得,解得.所以y与x的关系式为y=x+14.
因此放水前y与x的关系式为y=x+14(0≤x<8).
通过观察数据发现:8×18=10×14.4=12×1216×9=18×8=20×7.2=144.
因此放水后y与x的关系符合反比例函数,关系式为y=(x≥8).
所以开闸放水前和放水后最符合表中数据的函数解析式为y=x+4(0≤x<8)和y=(x≥8).
(3)当y=6时,6=,解得x=24,因此预计24h水位达到6 m.
19.解析 (1)∵△AOC的面积为4,∴.
解得k=-8或k=8(不符合题意,舍去).
∴反比例函数的关系式为y=-.
把点A(-2,a)和点B(b,-1)代入y=-,得a=4,b=8.
(2)不等式mx+n>的解集为x<-2或0<x<8.
(3)设点A(-2,4)关于y轴的对称点为A′,则A′的坐标为(2,4).
则直线A′B与y轴的交点即为所求的点P.
设直线AB的关系式为y=cx+d(c≠0),则有,解得.
∴直线AB的关系式为y=-x+.
∵直线y=-x+与y轴的交点坐标为(0,),∴点P的坐标为(0,).
20.解析 (1)函数图象如图所示.
(2)若0<x1<x2≤1,则y1>y2;若1<x1<x2,则y1<y2;若x1·x2=1,则y1=y2,
故填>;<;=.
(3)①由题意,y=1+(2x+)×0.5=1+x+(x>0).
②当y=3.5时,1+x+=3.5,解得x1=,x2=2.
∴当y≤3.5时,≤x≤2.
∴水池底面一边的长x应控制在,≤x≤2的范围内.
_21?????????è?????(www.21cnjy.com)_
