第二十三章 旋转(2课时)
文档属性
| 名称 | 第二十三章 旋转(2课时) |

|
|
| 格式 | zip | ||
| 文件大小 | 116.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-20 21:56:17 | ||
图片预览



文档简介
第二十三章 旋转
(第一课时) 23.1 图形的旋转
一、教材解读 自主预习,名师解读释疑
1.知识要点
(1)旋转的概念 在 内,将一个图形绕一个 沿 转动一个 的图形变换。
定点叫做 ,旋转的角叫做 ,如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.
(2)旋转三要素:① 旋转中心;② 旋转方向;③ 旋转角度.
(3)旋转的性质:
① 对应点到旋转中心的距离相等.
② 对应点与旋转中心所连线段的夹角等于旋转角.
③ 旋转前、后的图形全等
2.理解与注意
(1)图形的旋转是由旋转中心和旋转角决定的,而旋转角就包括旋转方向和旋转角度两个要素.
(2)容易被忽视的旋转角如图23.1-1,△ABC绕A逆时针旋转60到△AB′C′,除了∠CAC′ =∠BAB′ = 60外,对应线段BC与BC′ 的延长线相交形成的角也是旋转角即∠CAC′ = 60.
二、典型问题 典例剖析,专家点拨解惑
例1 如图,△ABC绕逆时针旋转90到△ADE.说出旋转中心、∠B的对应角、线段BC的对应线段,说出线段BC和DE的关系,连结BD,说明△ABD的形状
解:(1)旋转中心是A、∠B的对应角是∠D、线段BC的对应线段是线段DE.
(2)线段BC和DE的关系式相等且垂直.
(3)△ABD是等腰直角三角形.
说明:线段BC和DE的关系除了对应线段相等之外,它们延长线的夹角也符合对应线段的夹角为旋转角的性质,即等于90.本例主要要求能够理解图形旋转的特征.
变式1 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A沿逆时针方向旋转到△ABD′ 的位置,则∠ADD′ 的度数是( ).
A.250 B.300 C.350 D.450
变式2 (2009年陕西)如图,∠AOB = 900,∠B = 300,∠A′OB′ 可以看做是由∠AOB绕点O沿顺时针方向旋转 角度得到的,若点A′ 在AB上,则旋转角 可以是( ).
A.300 B.450 C.600 D.900
变式2图 变式3图 例2图
变式3 如图,△ABC与△ADE均为等边三角形,则图中可以看作是旋转关系的三角形是( ).
A.△ABC与△ADE B.△ABC与△ABD
C.△ABD与△ACE D.△ACE与△ADE
例2 如图,在△ABC中,∠ABC = 900,AB = AC,点D为△ABC内一点,且DA = 1,DC = 2,DB = 3.
(1)作出△ACD绕点C顺时针旋转900后所得△BCE;
(2)连结DE,说明△BDE的形状;
(3)求∠ADC的度数.
解 (1)如图所示△BCE为所求作三角形.
(2)△BDE为直角三角形,证明如下:
由(1)得BE = AD = 1,CE = CD = 2,∠DCE = 90.
∵ BE2 = CE2 + DE2 = 8,∴ BD2 = DE2 + BE2 = 9,∴ △BDE为直角三角形.
(3)由(1)得∠ADC =∠CEB = 450 + 900 = 1350.
说明:本题利用旋转变换,通过等量代换将分散的线段集中到一个三角形中,再证明这个三角形为直角三角形,运用勾股定理逆定理证明.
三、归纳小结 回味反思,领悟才能提高
1.知识线路:旋转的概念 → 旋转的性质 → 线段(角相等)
2.思想方法:整体思想
四、阶梯训练 自主练兵,会做才算懂了
A组:基础练习
1.下列现象属于旋转的是( ).
A.空中飞舞雪花 B.摩托车在急刹车时向前滑动
C.幸运大转盘转动的过程 D.飞机起飞后冲向空中的过程
2.△ABC绕点A旋转后得到△AFE,已知∠A = 700,则∠EAF的度数是( ).
A.500 B.700 C.1300 D.1100
3.有下列四个说法,其中正确说法的个数是( ).
①图形旋转时,位置保持不变的点只有旋转中心;
②图形旋转时,图形上的每一个点都绕着旋转中心旋转了相同的角度;
③图形旋转时,对应点与旋转中心的距离相等;
④图形旋转时,对应线段相等,对应角相等,图形的形状和大小都没有发生变化
A.1个 B.2个 C.3个 D.4个
4.如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( ).
A.∠BOF B.∠AOD C.∠COE D.∠COF
4题图 5题图
5.若正方形DCEF旋转后能与正方形ABCD重合,则图形所在平面内可作为旋转中心的点共有( )个.
A.1 B.2 C.3 D.4
6、(2009年淄博市)如图,四边形EFGH是由四边形经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形旋转得到四边形EFGH时的旋转中心用有序数对表示是 .
7.△AOB旋转到△A′OB′的位置.若∠AOA′=90°,则旋转中心是点______.旋转角是______.点A的对应点是______.线段AB的对应线段是______.∠B的对应角是______.∠BOB′=______.
8.如图,长方形ABCD绕顶点A旋转后得到长方形AEFG,那么:
(1)旋转角度为
(2)点C的对应点是
(3)线段AC的对应线段是
(4)∠CAB的对应角是 ,△ACF的形状为 三角形
9.如图,正三角形ABC绕其中心O至少旋转______度,可与其自身重合.
B组:拓展练习
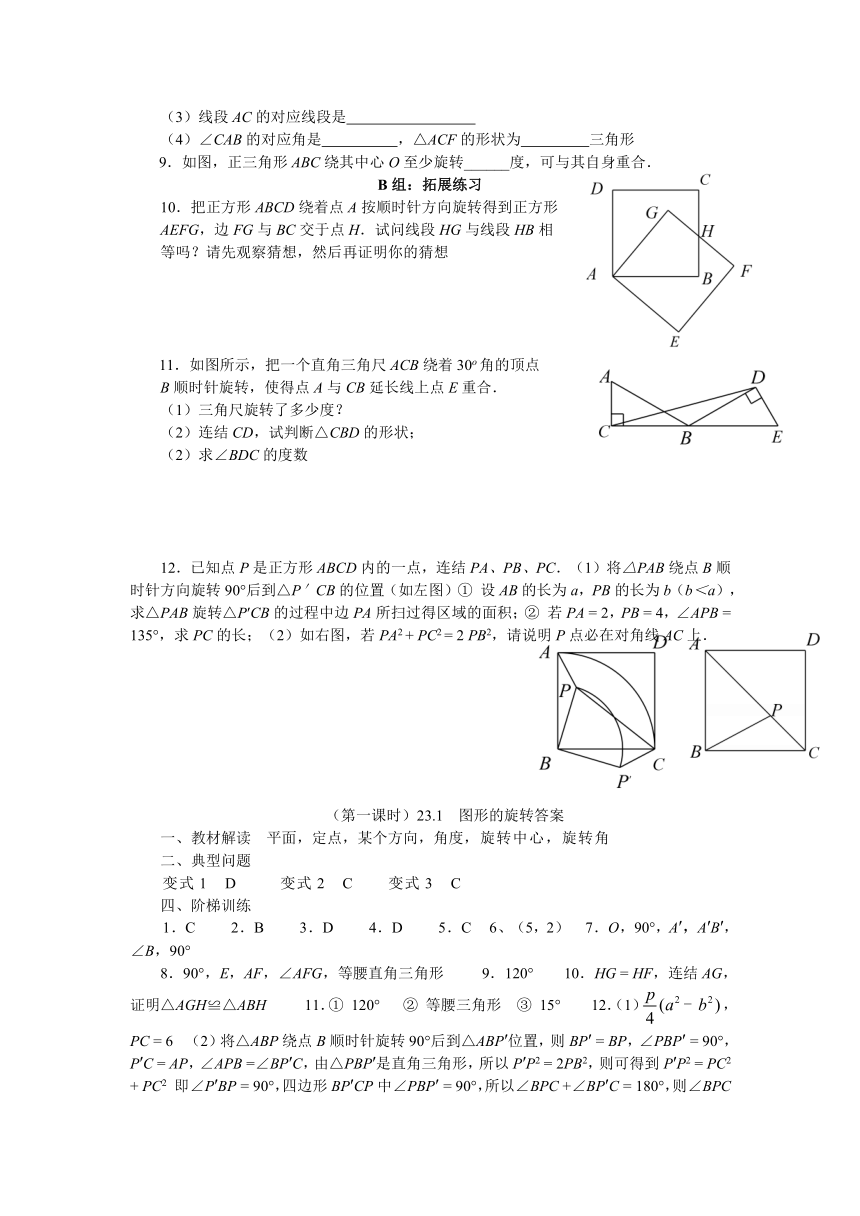
10.把正方形ABCD绕着点A按顺时针方向旋转得到正方形
AEFG,边FG与BC交于点H.试问线段HG与线段HB相
等吗?请先观察猜想,然后再证明你的猜想
11.如图所示,把一个直角三角尺ACB绕着30o角的顶点
B顺时针旋转,使得点A与CB延长线上点E重合.
(1)三角尺旋转了多少度?
(2)连结CD,试判断△CBD的形状;
(2)求∠BDC的度数
12.已知点P是正方形ABCD内的一点,连结PA、PB、PC.(1)将△PAB绕点B顺时针方向旋转90°后到△P′CB的位置(如左图)① 设AB的长为a,PB的长为b(b<a),求△PAB旋转△P′CB的过程中边PA所扫过得区域的面积;② 若PA = 2,PB = 4,∠APB = 135°,求PC的长;(2)如右图,若PA2 + PC2 = 2 PB2,请说明P点必在对角线AC上.
(第一课时)23.1 图形的旋转答案
一、教材解读 平面,定点,某个方向,角度,旋转中心,旋转角
二、典型问题
变式1 D 变式2 C 变式3 C
四、阶梯训练
1.C 2.B 3.D 4.D 5.C 6、(5,2) 7.O,90°,A′,A′B′,∠B,90°
8.90°,E,AF,∠AFG,等腰直角三角形 9.120° 10.HG = HF,连结AG,证明△AGH≌△ABH 11.① 120° ② 等腰三角形 ③ 15° 12.(1),PC = 6 (2)将△ABP绕点B顺时针旋转90°后到△ABP′位置,则BP′ = BP,∠PBP′ = 90°,P′C = AP,∠APB =∠BP′C,由△PBP′是直角三角形,所以P′P2 = 2PB2,则可得到P′P2 = PC2 + PC2 即∠P′BP = 90°,四边形BP′CP中∠PBP′ = 90°,所以∠BPC +∠BP′C = 180°,则∠BPC +∠APC = 180°,所以点P在AC上.
(第二课时)23.1 图形的旋转
一、教材解读 自主预习,名师解读释疑
1.知识要点
(1)作一个图形旋转后的图形是根据旋转的性质:对应点到 的距离相等,每个对应点都旋转 的角度.
(2)作旋转图形的一般步骤:明确三要素: ;确定关键点,作出它们旋转后的 ;顺次连结对应点
(3)旋转对称图形:一个图形绕 旋转一定度数后能与 重合,这种图形称为旋转对称图形,旋转对称图形的旋转角为 .
2.理解与注意
① 作图要先确定图形的“关键点”,用局部带动整体运行旋转
② 三要素中只要任意改变一个,图形就会不一样.
二、典型问题 典例剖析,专家点拨解惑
例1 如图所示,作出△ABC绕点O顺时针旋转一定角度后,
使得点A落在A′,试做出旋转后的图形.
解:(1)连结AO、A′O,量出∠AOA′的角度;(2)连结BO,沿顺时针方向做∠BOB′=∠AOA′,且OB′= OB;(3)同理作出点C的对应点C′;(4)顺次连结A′、B′、C′,则∠A′B′C′ 为所求.
说明:本题只告诉了A的对应点A′,没有告诉旋转角度,所以要先量出∠AOA′ 的度数作为旋转角;作图的时候要注意对应点与旋转中心的连线应该用虚线.
变式1 如左图,在单位网格中画出所给四边形ABCD绕O顺时针旋转90°后的图形A′B′C′D′.
解 连结OA,沿顺时针方向作∠A′OA = 90°,AO = A′O,则A′点为A的对应点,同理作出B、C、D的对应点B′、C′、D′,顺次连结A′、B′、C′、D′,四边形A′B′C′D′为所求.
变式2 已知如右图,线段CD是由线段AB经过旋转变换得到的.求旋转中心O点.
解:连结AC、BD,分别作两线段的中垂线,则中垂线的交点O为所求.
说明:往往同学们会做已知旋转中心和旋转角,求旋转之后的图形,但对于求旋转中心的例子却很陌生,其实这里也是利用了旋转的性质,对应点到旋转中心的距离相等,从而发现中心应该在对应点连线段的中垂线上.
例2 如图可以看做一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数可以是 .
变式1 下列图形中,旋转60°后能和原图形重合的是( ).A
A.正六边形 B.正五边形 C.正方形 D.正三角形
变式2 所示是三个菱形,它可以看作是什么“基本图形”通过怎样的旋转而得到?
分析 基本图形是一个菱形,共旋转3次,所以,旋转角为120°.
三、归纳小结 回味反思,领悟才能提高
1.知识结构:旋转的性质 → 旋转的作图 → 图形的设计
2.思想方法:
四、阶梯训练 自主练兵,会做才算懂了
A组:基础练习
1.等边三角形绕着它的中心旋转一周,可与原图形重合的次数是( ). C
A.1 B.2 C.3 D.4
2.有一种平面图形,它绕着中心旋转,不论旋转多少度,所得到的图形都与原图形完全重合你觉得它可能是( ). D
A.三角形 B.等边三角形 C.正方形 D.圆
3.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转
多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同
学说:135°.以上四位同学的回答中,错误的是( ). B
A.甲 B.乙 C.丙 D.丁
4.(2009·梅州市)如图所示,五角星的顶点是一个正五边形的五个顶点.
这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过______
_____次旋转而得到, 每一次旋转______度. 4,72
5.(2009·衡阳市)点A的坐标为(,0),把点A绕着坐标原点顺时
针旋转135 到点B,那么点B的坐标是 . (1,1)
6.把边长为2 cm的正方形ABCD,绕着点D逆时针旋转45°后,
变为正方形A′B′C′D′,作出上述图形
解 略
7.如图,已知有两个同心圆,半径OA、OB成30°角,OB与小圆交于C点,若把△ABC每次绕O点逆时针旋转30°,试画出所得的图形.
B组:拓展练习
8.正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,如果两个正方形的边长相等,那么正方形A′B′C′O绕点O重叠部分的面积是多少?你能求出来,并说明理由吗?
9.(2008·河南省)复习“全等三角形”的知识时,老师布置了一道作业题:如图①,已知在△ABC中,AB = AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP =∠BAC,连结BQ、CP,则BQ = CP.小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ = CP,他将点P移到等腰三角形ABC之外,原题中其他条件不变,发现“BQ = CP”仍然成立,请你就图②给出证明.
10.(2010·东莞市)如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
(1)将原来的Rt△ABC绕点O顺时针旋转90°得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形;(2)求线段BC扫过的面积;(3)求点A旋转到A1路径长.
答:(1)略
(2)2p
(3)
(第二课时)23.1 图形的旋转答案
一、教材解读
1.知识要点 (1)旋转中心,相同 (2)旋转中心、旋转方向、旋转角度,对应点 (3)一个点,自己,
二、典型问题
例2 45°
变式1 A
变式2 基本图形是菱形,沿旋转中心每次旋转120°就得到这个图案.
四、阶梯训练
1.C 2.D 3.B 4.4,72 5.(1,1)
6. 7
8.正方形面积的 9.仍然证明
△ABQ≌△ACP,从而证得BQ = CP.
变式1图
图23.1-1
例1图
A
B
C
D
E
F
(第6题)
G
H
C
A
B
O
A′
O
D
C
B
A
A
B
C
D
(第一课时) 23.1 图形的旋转
一、教材解读 自主预习,名师解读释疑
1.知识要点
(1)旋转的概念 在 内,将一个图形绕一个 沿 转动一个 的图形变换。
定点叫做 ,旋转的角叫做 ,如果图形上的点P经过旋转变为点P′,那么这两个点叫做这个旋转的对应点.
(2)旋转三要素:① 旋转中心;② 旋转方向;③ 旋转角度.
(3)旋转的性质:
① 对应点到旋转中心的距离相等.
② 对应点与旋转中心所连线段的夹角等于旋转角.
③ 旋转前、后的图形全等
2.理解与注意
(1)图形的旋转是由旋转中心和旋转角决定的,而旋转角就包括旋转方向和旋转角度两个要素.
(2)容易被忽视的旋转角如图23.1-1,△ABC绕A逆时针旋转60到△AB′C′,除了∠CAC′ =∠BAB′ = 60外,对应线段BC与BC′ 的延长线相交形成的角也是旋转角即∠CAC′ = 60.
二、典型问题 典例剖析,专家点拨解惑
例1 如图,△ABC绕逆时针旋转90到△ADE.说出旋转中心、∠B的对应角、线段BC的对应线段,说出线段BC和DE的关系,连结BD,说明△ABD的形状
解:(1)旋转中心是A、∠B的对应角是∠D、线段BC的对应线段是线段DE.
(2)线段BC和DE的关系式相等且垂直.
(3)△ABD是等腰直角三角形.
说明:线段BC和DE的关系除了对应线段相等之外,它们延长线的夹角也符合对应线段的夹角为旋转角的性质,即等于90.本例主要要求能够理解图形旋转的特征.
变式1 如图,D是等腰直角三角形ABC内一点,BC是斜边,如果将△ABD绕点A沿逆时针方向旋转到△ABD′ 的位置,则∠ADD′ 的度数是( ).
A.250 B.300 C.350 D.450
变式2 (2009年陕西)如图,∠AOB = 900,∠B = 300,∠A′OB′ 可以看做是由∠AOB绕点O沿顺时针方向旋转 角度得到的,若点A′ 在AB上,则旋转角 可以是( ).
A.300 B.450 C.600 D.900
变式2图 变式3图 例2图
变式3 如图,△ABC与△ADE均为等边三角形,则图中可以看作是旋转关系的三角形是( ).
A.△ABC与△ADE B.△ABC与△ABD
C.△ABD与△ACE D.△ACE与△ADE
例2 如图,在△ABC中,∠ABC = 900,AB = AC,点D为△ABC内一点,且DA = 1,DC = 2,DB = 3.
(1)作出△ACD绕点C顺时针旋转900后所得△BCE;
(2)连结DE,说明△BDE的形状;
(3)求∠ADC的度数.
解 (1)如图所示△BCE为所求作三角形.
(2)△BDE为直角三角形,证明如下:
由(1)得BE = AD = 1,CE = CD = 2,∠DCE = 90.
∵ BE2 = CE2 + DE2 = 8,∴ BD2 = DE2 + BE2 = 9,∴ △BDE为直角三角形.
(3)由(1)得∠ADC =∠CEB = 450 + 900 = 1350.
说明:本题利用旋转变换,通过等量代换将分散的线段集中到一个三角形中,再证明这个三角形为直角三角形,运用勾股定理逆定理证明.
三、归纳小结 回味反思,领悟才能提高
1.知识线路:旋转的概念 → 旋转的性质 → 线段(角相等)
2.思想方法:整体思想
四、阶梯训练 自主练兵,会做才算懂了
A组:基础练习
1.下列现象属于旋转的是( ).
A.空中飞舞雪花 B.摩托车在急刹车时向前滑动
C.幸运大转盘转动的过程 D.飞机起飞后冲向空中的过程
2.△ABC绕点A旋转后得到△AFE,已知∠A = 700,则∠EAF的度数是( ).
A.500 B.700 C.1300 D.1100
3.有下列四个说法,其中正确说法的个数是( ).
①图形旋转时,位置保持不变的点只有旋转中心;
②图形旋转时,图形上的每一个点都绕着旋转中心旋转了相同的角度;
③图形旋转时,对应点与旋转中心的距离相等;
④图形旋转时,对应线段相等,对应角相等,图形的形状和大小都没有发生变化
A.1个 B.2个 C.3个 D.4个
4.如图,把菱形ABOC绕点O顺时针旋转得到菱形DFOE,则下列角中不是旋转角的为( ).
A.∠BOF B.∠AOD C.∠COE D.∠COF
4题图 5题图
5.若正方形DCEF旋转后能与正方形ABCD重合,则图形所在平面内可作为旋转中心的点共有( )个.
A.1 B.2 C.3 D.4
6、(2009年淄博市)如图,四边形EFGH是由四边形经过旋转得到的.如果用有序数对(2,1)表示方格纸上A点的位置,用(1,2)表示B点的位置,那么四边形旋转得到四边形EFGH时的旋转中心用有序数对表示是 .
7.△AOB旋转到△A′OB′的位置.若∠AOA′=90°,则旋转中心是点______.旋转角是______.点A的对应点是______.线段AB的对应线段是______.∠B的对应角是______.∠BOB′=______.
8.如图,长方形ABCD绕顶点A旋转后得到长方形AEFG,那么:
(1)旋转角度为
(2)点C的对应点是
(3)线段AC的对应线段是
(4)∠CAB的对应角是 ,△ACF的形状为 三角形
9.如图,正三角形ABC绕其中心O至少旋转______度,可与其自身重合.
B组:拓展练习
10.把正方形ABCD绕着点A按顺时针方向旋转得到正方形
AEFG,边FG与BC交于点H.试问线段HG与线段HB相
等吗?请先观察猜想,然后再证明你的猜想
11.如图所示,把一个直角三角尺ACB绕着30o角的顶点
B顺时针旋转,使得点A与CB延长线上点E重合.
(1)三角尺旋转了多少度?
(2)连结CD,试判断△CBD的形状;
(2)求∠BDC的度数
12.已知点P是正方形ABCD内的一点,连结PA、PB、PC.(1)将△PAB绕点B顺时针方向旋转90°后到△P′CB的位置(如左图)① 设AB的长为a,PB的长为b(b<a),求△PAB旋转△P′CB的过程中边PA所扫过得区域的面积;② 若PA = 2,PB = 4,∠APB = 135°,求PC的长;(2)如右图,若PA2 + PC2 = 2 PB2,请说明P点必在对角线AC上.
(第一课时)23.1 图形的旋转答案
一、教材解读 平面,定点,某个方向,角度,旋转中心,旋转角
二、典型问题
变式1 D 变式2 C 变式3 C
四、阶梯训练
1.C 2.B 3.D 4.D 5.C 6、(5,2) 7.O,90°,A′,A′B′,∠B,90°
8.90°,E,AF,∠AFG,等腰直角三角形 9.120° 10.HG = HF,连结AG,证明△AGH≌△ABH 11.① 120° ② 等腰三角形 ③ 15° 12.(1),PC = 6 (2)将△ABP绕点B顺时针旋转90°后到△ABP′位置,则BP′ = BP,∠PBP′ = 90°,P′C = AP,∠APB =∠BP′C,由△PBP′是直角三角形,所以P′P2 = 2PB2,则可得到P′P2 = PC2 + PC2 即∠P′BP = 90°,四边形BP′CP中∠PBP′ = 90°,所以∠BPC +∠BP′C = 180°,则∠BPC +∠APC = 180°,所以点P在AC上.
(第二课时)23.1 图形的旋转
一、教材解读 自主预习,名师解读释疑
1.知识要点
(1)作一个图形旋转后的图形是根据旋转的性质:对应点到 的距离相等,每个对应点都旋转 的角度.
(2)作旋转图形的一般步骤:明确三要素: ;确定关键点,作出它们旋转后的 ;顺次连结对应点
(3)旋转对称图形:一个图形绕 旋转一定度数后能与 重合,这种图形称为旋转对称图形,旋转对称图形的旋转角为 .
2.理解与注意
① 作图要先确定图形的“关键点”,用局部带动整体运行旋转
② 三要素中只要任意改变一个,图形就会不一样.
二、典型问题 典例剖析,专家点拨解惑
例1 如图所示,作出△ABC绕点O顺时针旋转一定角度后,
使得点A落在A′,试做出旋转后的图形.
解:(1)连结AO、A′O,量出∠AOA′的角度;(2)连结BO,沿顺时针方向做∠BOB′=∠AOA′,且OB′= OB;(3)同理作出点C的对应点C′;(4)顺次连结A′、B′、C′,则∠A′B′C′ 为所求.
说明:本题只告诉了A的对应点A′,没有告诉旋转角度,所以要先量出∠AOA′ 的度数作为旋转角;作图的时候要注意对应点与旋转中心的连线应该用虚线.
变式1 如左图,在单位网格中画出所给四边形ABCD绕O顺时针旋转90°后的图形A′B′C′D′.
解 连结OA,沿顺时针方向作∠A′OA = 90°,AO = A′O,则A′点为A的对应点,同理作出B、C、D的对应点B′、C′、D′,顺次连结A′、B′、C′、D′,四边形A′B′C′D′为所求.
变式2 已知如右图,线段CD是由线段AB经过旋转变换得到的.求旋转中心O点.
解:连结AC、BD,分别作两线段的中垂线,则中垂线的交点O为所求.
说明:往往同学们会做已知旋转中心和旋转角,求旋转之后的图形,但对于求旋转中心的例子却很陌生,其实这里也是利用了旋转的性质,对应点到旋转中心的距离相等,从而发现中心应该在对应点连线段的中垂线上.
例2 如图可以看做一个等腰直角三角形旋转若干次而生成的,则每次旋转的度数可以是 .
变式1 下列图形中,旋转60°后能和原图形重合的是( ).A
A.正六边形 B.正五边形 C.正方形 D.正三角形
变式2 所示是三个菱形,它可以看作是什么“基本图形”通过怎样的旋转而得到?
分析 基本图形是一个菱形,共旋转3次,所以,旋转角为120°.
三、归纳小结 回味反思,领悟才能提高
1.知识结构:旋转的性质 → 旋转的作图 → 图形的设计
2.思想方法:
四、阶梯训练 自主练兵,会做才算懂了
A组:基础练习
1.等边三角形绕着它的中心旋转一周,可与原图形重合的次数是( ). C
A.1 B.2 C.3 D.4
2.有一种平面图形,它绕着中心旋转,不论旋转多少度,所得到的图形都与原图形完全重合你觉得它可能是( ). D
A.三角形 B.等边三角形 C.正方形 D.圆
3.数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转
多少度后和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同
学说:135°.以上四位同学的回答中,错误的是( ). B
A.甲 B.乙 C.丙 D.丁
4.(2009·梅州市)如图所示,五角星的顶点是一个正五边形的五个顶点.
这个五角星可以由一个基本图形(图中的阴影部分)绕中心O至少经过______
_____次旋转而得到, 每一次旋转______度. 4,72
5.(2009·衡阳市)点A的坐标为(,0),把点A绕着坐标原点顺时
针旋转135 到点B,那么点B的坐标是 . (1,1)
6.把边长为2 cm的正方形ABCD,绕着点D逆时针旋转45°后,
变为正方形A′B′C′D′,作出上述图形
解 略
7.如图,已知有两个同心圆,半径OA、OB成30°角,OB与小圆交于C点,若把△ABC每次绕O点逆时针旋转30°,试画出所得的图形.
B组:拓展练习
8.正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点,如果两个正方形的边长相等,那么正方形A′B′C′O绕点O重叠部分的面积是多少?你能求出来,并说明理由吗?
9.(2008·河南省)复习“全等三角形”的知识时,老师布置了一道作业题:如图①,已知在△ABC中,AB = AC,P是△ABC内任意一点,将AP绕点A顺时针旋转至AQ,使∠QAP =∠BAC,连结BQ、CP,则BQ = CP.小亮是个爱动脑筋的同学,他通过对图①的分析,证明了△ABQ≌△ACP,从而证得BQ = CP,他将点P移到等腰三角形ABC之外,原题中其他条件不变,发现“BQ = CP”仍然成立,请你就图②给出证明.
10.(2010·东莞市)如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在格点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
(1)将原来的Rt△ABC绕点O顺时针旋转90°得到Rt△A1B1C1,试在图上画出Rt△A1B1C1的图形;(2)求线段BC扫过的面积;(3)求点A旋转到A1路径长.
答:(1)略
(2)2p
(3)
(第二课时)23.1 图形的旋转答案
一、教材解读
1.知识要点 (1)旋转中心,相同 (2)旋转中心、旋转方向、旋转角度,对应点 (3)一个点,自己,
二、典型问题
例2 45°
变式1 A
变式2 基本图形是菱形,沿旋转中心每次旋转120°就得到这个图案.
四、阶梯训练
1.C 2.D 3.B 4.4,72 5.(1,1)
6. 7
8.正方形面积的 9.仍然证明
△ABQ≌△ACP,从而证得BQ = CP.
变式1图
图23.1-1
例1图
A
B
C
D
E
F
(第6题)
G
H
C
A
B
O
A′
O
D
C
B
A
A
B
C
D
同课章节目录
