福建省四地六校2011-2012学年高二下学期第二次月考试题数学文
文档属性
| 名称 | 福建省四地六校2011-2012学年高二下学期第二次月考试题数学文 |  | |
| 格式 | zip | ||
| 文件大小 | 121.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-20 22:02:02 | ||
图片预览




文档简介
“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考
2011-2012学年下学期第二次月考
高二文科数学试题
(考试时间:120分钟 总分:150分)
一、选择题(每题5分,共60分)
1、已知集合A={1,2,3,5},B={2,4,5,6},则=
A.{1,2} B.{2,3} C.{2,5} D.{4,6}
2、下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程必过();
④在一个2×2列联中,由计算得则有99.9%的把握确认这两个变量间有关系;
` 其中错误的个数是 ( )
A.0 B.1 C.2 D.3
本题可以参考独立性检验临界值表:
0.5 0.40 0.25 0.15 0.10 0.05 0.25 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.535 7.879 10.828
3、今有甲、乙、丙、丁四人通过“拔河”进行“体力”较量。当甲、乙两人为一方,丙、丁两人为另一方时,双方势均力敌;当甲与丙对调以后,甲、丁一方轻而易举地战胜了乙、丙一方;而乙凭其一人之力便战胜了甲、丙两人的组合。那么,甲、乙、丙、丁四人的“体力”由强到弱的顺序是
A.丁、乙、甲、丙 B.乙、丁、甲、丙 C.丁、乙、丙、甲 D.乙、丁、丙、甲
4、 若复数是虚数单位),且是纯虚数,则等于( )
A. B. C. D.40
5、已知复数,则的共轭复数
(A) (B) (C) (D)
6、若集合,,则“”是“”的
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分又不必要条件
7、已知下面两个程序:
甲: i=1 乙:i=1000
S=0 S=0
WHILE i<=1000 DO
S=S+i S=S+i
i=i+l i=i-1
WEND LOOP UNTIL i<1
PRINT S PRINT S
END END
对甲、乙两程序和输出结果判断正确的是 ( )
A.程序不同,结果不同 B.程序不同,结果相同
C.程序相同,结果不同 D.程序相同,结果相同
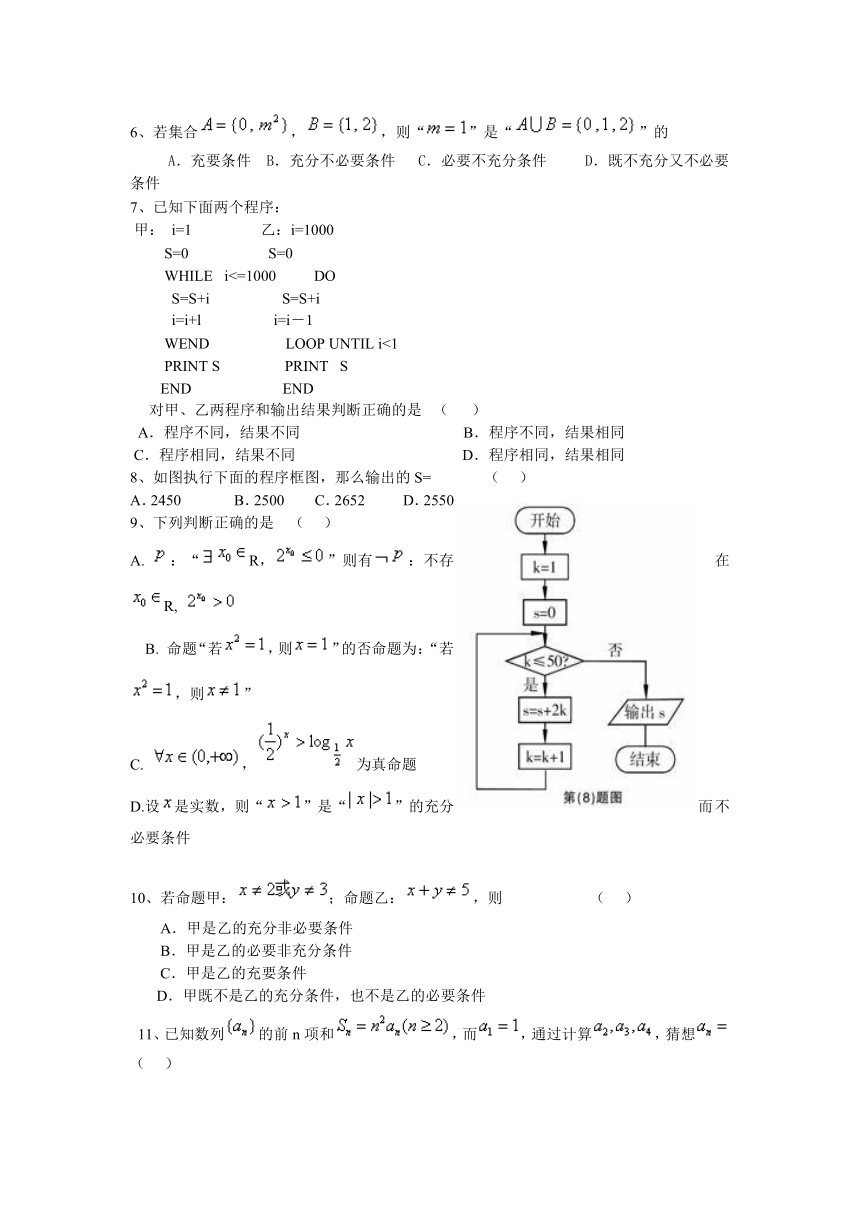
8、如图执行下面的程序框图,那么输出的S= ( )
A.2450 B.2500 C.2652 D.2550
9、下列判断正确的是 ( )
A. :“R,”则有:不存在R,
B. 命题“若,则”的否命题为:“若,则”
C. ,为真命题
D.设是实数,则“”是“”的充分而不必要条件
10、若命题甲:;命题乙:,则 ( )
A.甲是乙的充分非必要条件
B.甲是乙的必要非充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件,也不是乙的必要条件
11、已知数列的前n项和,而,通过计算,猜想( )
A、 B、 C、 D、
12.已知,则的解析式为( )
A. B. C. D.
二、填空题(每题4 分,共16 分)
13、函数的定义域是______________.
14、若函数的值域是,则函数的值域是_______;
15、设函数f(x)=,若f(a)=4,则实数a= ;
16、定义集合运算:A⊙B={z|z=xy(x+y),x∈A,y∈B}.设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为 .
三.计算题(17——21每题12分,22题14分)
17.设集合AB
(1)若AB求实数a的值;
(2)若AB=A求实数a的取值范围;
18.已知命题若非是的充分不必要条件,求的取值范围。
19.定义在实数R上的函数y= f(x)是偶函数,当x≥0时,.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明)
20、已知函数f(x)=- + (x>0).
(1)解关于x的不等式f(x)>0;
(2)若f(x)+2x≥0在(0,+∞)上恒成立,求a的取值范围.
21.已知函数=为奇函数、∈ ,=2,<3
(1)求的解析式;
(2)当<0时,确定的单调递增区间,并给予证明(可用导数)
22.已知函数()是偶函数且
(1)求函数的解析式;
(2)是否存在实数,使函数在区间 上的值域为 若存在,求出 的值;若不存在,说明理由.
“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考
2011-2012学年上学期第二次月考
高二文科数学试题答题卷
(考试时间:120分钟 总分:150分)
题 号 一 二 17 18 19 20 21 22 总分
得 分
一、单项选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4小题,共16分)
13___________ 14.__________, 15__________ , 16___________
三.解答题(12+12+12+12+12+14=74分 解答应写出文字说明、证明过程或演算步骤
17. (本小题满分12分)
18. (本小题满分12分)
19. (本小题满分12分)
20. (本小题满分12分)
21. (本小题满分12分)
22. (本小题满分14分)
“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考
2011-2012学年下学期第二次月考
高二文科数学参考答案
一选择题
1.C 2.B 3.A 4.B 5.C 6.B 7. B 8.D 9.D 10.B 11.B 12.C
二、填空题
13、 14、 15、或2 16、18
三.计算题
17.设集合AB
(1)若AB求实数a的值;
(2)若AB=A求实数a的取值范围;
解 由x2-3x+2=0得x=1或x=2,故集合A= ..........2分
(1)∵AB∴2B,代入B中的方程,得a2+4a+3=0,∴a=-1或a=-3; ....................4分
当a=-1时,B=满足条件;
当a=-3时,B=满足条件;
综上,a的值为-1或-3. .........................6分
(2)对于集合B,=4(a+1)2-4(a2-5)=8(a+3).
∵AB=A∴BA,.................................8分
①当<0,即a<-3时,B=,满足条件;
②当=0,即a=-3时,B=,满足条件;
③当>0,即a>-3时,B=A=才能满足条件, 则由根与系数的关系得
即矛盾;
综上,a的取值范围是a≤-3. ..................... 12分
18.已知命题若非是的充分不必要条件,求的取值范围。
解:..........4分
.............8分
而..............................10分
即。.......................12分
19.定义在实数R上的函数y= f(x)是偶函数,当x≥0时,.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).
解:(Ⅰ)设x<0,则- x>0, ∵f(x)是偶函数,
∴f(-x)=f(x) ∴x<0时,
所以 。。。。。。。。6分
(Ⅱ)y=f(x)开口向下,所以y=f(x)有最大值f(1)=f(-1)=1.。。。。。。9分
函数y=f(x)的单调递增区间是(-∞,-1和[0,1]
单调递减区间是 [-1,0]和[1,+∞。。12分
20、已知函数f(x)=- + (x>0).
(1)解关于x的不等式f(x)>0;
(2)若f(x)+2x≥0在(0,+∞)上恒成立,求a的取值范围.
解:(1)不等式f(x)>0,即-+>0,
即>0.整理成(x-2a)·ax<0.
①当a>0时,不等式x(x-2a)<0,
不等式的解为0②当a<0时,不等式x(x-2a)>0,
不等式的解为x>0或x<2a(舍去).
综上,a>0时,不等式解集为{x|00}.。。。。。。。。。6分
(2)若f(x)+2x≥0在(0,+∞)上恒成立,
即-++2x≥0,
∴≤2.
∵2的最小值为4,
故≤4,解得a<0或a≥.。。。。。。。。。。。。。。。。12分
21.已知函数=为奇函数、∈Z+,=2,<3
(1)求的解析式;
(2)当<0时,确定的单调递增区间,并给予证明
(可用导数)
解:(1)∵函数为奇函数,
∴=0.........................2分
,得:=1,=1.即:=..6分
当<0时,
的单调递增区间是-∞,-1.........8分
证明...............12分
22.已知函数()是偶函数且
(1)求函数的解析式;
(2)是否存在实数,使函数在区间 上的值域为 若存在,求出 的值;若不存在,说明理由.
(1)对于任意恒成立。。。。。4分
(2)由(1)得f(x)= x 2 , ∴ g (x) = 1-λ x2 + (2 λ-1) x
又 ∴ g(x) = =
故 g(x) 的对称轴为
∵ ∴ ∴
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
方法一:
① ∵ x ∈[-1,2 ]
∴ 当 即 时,
;
= -1 不符合题意 舍去
② 当 即 ≥ 1时 ,
依题意得: 解得 : = 2
综上得:存在实数 = 2 满足题意。。。。。。。。。。。。。14分
方法二:
∵对称轴 且x ∈[-1,2 ] ,图像开口向下
∴
依题意 g(x)max = ∴=
解得: (舍去) 或
检验:当时,g(x)=
∵ x ∈[-1,2 ]
∴ x = 时,g(x)max = , x = -1 时= -4
符合题意。
综上得 :
-1
2
1
2
1
-1
2011-2012学年下学期第二次月考
高二文科数学试题
(考试时间:120分钟 总分:150分)
一、选择题(每题5分,共60分)
1、已知集合A={1,2,3,5},B={2,4,5,6},则=
A.{1,2} B.{2,3} C.{2,5} D.{4,6}
2、下列说法:
①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变;
②设有一个回归方程,变量x增加一个单位时,y平均增加5个单位;
③线性回归方程必过();
④在一个2×2列联中,由计算得则有99.9%的把握确认这两个变量间有关系;
` 其中错误的个数是 ( )
A.0 B.1 C.2 D.3
本题可以参考独立性检验临界值表:
0.5 0.40 0.25 0.15 0.10 0.05 0.25 0.010 0.005 0.001
k 0.455 0.708 1.323 2.072 2.706 3.841 5.024 6.535 7.879 10.828
3、今有甲、乙、丙、丁四人通过“拔河”进行“体力”较量。当甲、乙两人为一方,丙、丁两人为另一方时,双方势均力敌;当甲与丙对调以后,甲、丁一方轻而易举地战胜了乙、丙一方;而乙凭其一人之力便战胜了甲、丙两人的组合。那么,甲、乙、丙、丁四人的“体力”由强到弱的顺序是
A.丁、乙、甲、丙 B.乙、丁、甲、丙 C.丁、乙、丙、甲 D.乙、丁、丙、甲
4、 若复数是虚数单位),且是纯虚数,则等于( )
A. B. C. D.40
5、已知复数,则的共轭复数
(A) (B) (C) (D)
6、若集合,,则“”是“”的
A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分又不必要条件
7、已知下面两个程序:
甲: i=1 乙:i=1000
S=0 S=0
WHILE i<=1000 DO
S=S+i S=S+i
i=i+l i=i-1
WEND LOOP UNTIL i<1
PRINT S PRINT S
END END
对甲、乙两程序和输出结果判断正确的是 ( )
A.程序不同,结果不同 B.程序不同,结果相同
C.程序相同,结果不同 D.程序相同,结果相同
8、如图执行下面的程序框图,那么输出的S= ( )
A.2450 B.2500 C.2652 D.2550
9、下列判断正确的是 ( )
A. :“R,”则有:不存在R,
B. 命题“若,则”的否命题为:“若,则”
C. ,为真命题
D.设是实数,则“”是“”的充分而不必要条件
10、若命题甲:;命题乙:,则 ( )
A.甲是乙的充分非必要条件
B.甲是乙的必要非充分条件
C.甲是乙的充要条件
D.甲既不是乙的充分条件,也不是乙的必要条件
11、已知数列的前n项和,而,通过计算,猜想( )
A、 B、 C、 D、
12.已知,则的解析式为( )
A. B. C. D.
二、填空题(每题4 分,共16 分)
13、函数的定义域是______________.
14、若函数的值域是,则函数的值域是_______;
15、设函数f(x)=,若f(a)=4,则实数a= ;
16、定义集合运算:A⊙B={z|z=xy(x+y),x∈A,y∈B}.设集合A={0,1},B={2,3},则集合A⊙B的所有元素之和为 .
三.计算题(17——21每题12分,22题14分)
17.设集合AB
(1)若AB求实数a的值;
(2)若AB=A求实数a的取值范围;
18.已知命题若非是的充分不必要条件,求的取值范围。
19.定义在实数R上的函数y= f(x)是偶函数,当x≥0时,.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明)
20、已知函数f(x)=- + (x>0).
(1)解关于x的不等式f(x)>0;
(2)若f(x)+2x≥0在(0,+∞)上恒成立,求a的取值范围.
21.已知函数=为奇函数、∈ ,=2,<3
(1)求的解析式;
(2)当<0时,确定的单调递增区间,并给予证明(可用导数)
22.已知函数()是偶函数且
(1)求函数的解析式;
(2)是否存在实数,使函数在区间 上的值域为 若存在,求出 的值;若不存在,说明理由.
“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考
2011-2012学年上学期第二次月考
高二文科数学试题答题卷
(考试时间:120分钟 总分:150分)
题 号 一 二 17 18 19 20 21 22 总分
得 分
一、单项选择题(每小题5分,共60分)
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4小题,共16分)
13___________ 14.__________, 15__________ , 16___________
三.解答题(12+12+12+12+12+14=74分 解答应写出文字说明、证明过程或演算步骤
17. (本小题满分12分)
18. (本小题满分12分)
19. (本小题满分12分)
20. (本小题满分12分)
21. (本小题满分12分)
22. (本小题满分14分)
“华安、连城、永安、漳平一中,龙海二中,泉港一中”六校联考
2011-2012学年下学期第二次月考
高二文科数学参考答案
一选择题
1.C 2.B 3.A 4.B 5.C 6.B 7. B 8.D 9.D 10.B 11.B 12.C
二、填空题
13、 14、 15、或2 16、18
三.计算题
17.设集合AB
(1)若AB求实数a的值;
(2)若AB=A求实数a的取值范围;
解 由x2-3x+2=0得x=1或x=2,故集合A= ..........2分
(1)∵AB∴2B,代入B中的方程,得a2+4a+3=0,∴a=-1或a=-3; ....................4分
当a=-1时,B=满足条件;
当a=-3时,B=满足条件;
综上,a的值为-1或-3. .........................6分
(2)对于集合B,=4(a+1)2-4(a2-5)=8(a+3).
∵AB=A∴BA,.................................8分
①当<0,即a<-3时,B=,满足条件;
②当=0,即a=-3时,B=,满足条件;
③当>0,即a>-3时,B=A=才能满足条件, 则由根与系数的关系得
即矛盾;
综上,a的取值范围是a≤-3. ..................... 12分
18.已知命题若非是的充分不必要条件,求的取值范围。
解:..........4分
.............8分
而..............................10分
即。.......................12分
19.定义在实数R上的函数y= f(x)是偶函数,当x≥0时,.
(Ⅰ)求f(x)在R上的表达式;
(Ⅱ)求y=f(x)的最大值,并写出f(x)在R上的单调区间(不必证明).
解:(Ⅰ)设x<0,则- x>0, ∵f(x)是偶函数,
∴f(-x)=f(x) ∴x<0时,
所以 。。。。。。。。6分
(Ⅱ)y=f(x)开口向下,所以y=f(x)有最大值f(1)=f(-1)=1.。。。。。。9分
函数y=f(x)的单调递增区间是(-∞,-1和[0,1]
单调递减区间是 [-1,0]和[1,+∞。。12分
20、已知函数f(x)=- + (x>0).
(1)解关于x的不等式f(x)>0;
(2)若f(x)+2x≥0在(0,+∞)上恒成立,求a的取值范围.
解:(1)不等式f(x)>0,即-+>0,
即>0.整理成(x-2a)·ax<0.
①当a>0时,不等式x(x-2a)<0,
不等式的解为0
不等式的解为x>0或x<2a(舍去).
综上,a>0时,不等式解集为{x|0
(2)若f(x)+2x≥0在(0,+∞)上恒成立,
即-++2x≥0,
∴≤2.
∵2的最小值为4,
故≤4,解得a<0或a≥.。。。。。。。。。。。。。。。。12分
21.已知函数=为奇函数、∈Z+,=2,<3
(1)求的解析式;
(2)当<0时,确定的单调递增区间,并给予证明
(可用导数)
解:(1)∵函数为奇函数,
∴=0.........................2分
,得:=1,=1.即:=..6分
当<0时,
的单调递增区间是-∞,-1.........8分
证明...............12分
22.已知函数()是偶函数且
(1)求函数的解析式;
(2)是否存在实数,使函数在区间 上的值域为 若存在,求出 的值;若不存在,说明理由.
(1)对于任意恒成立。。。。。4分
(2)由(1)得f(x)= x 2 , ∴ g (x) = 1-λ x2 + (2 λ-1) x
又 ∴ g(x) = =
故 g(x) 的对称轴为
∵ ∴ ∴
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。8分
方法一:
① ∵ x ∈[-1,2 ]
∴ 当 即 时,
;
= -1 不符合题意 舍去
② 当 即 ≥ 1时 ,
依题意得: 解得 : = 2
综上得:存在实数 = 2 满足题意。。。。。。。。。。。。。14分
方法二:
∵对称轴 且x ∈[-1,2 ] ,图像开口向下
∴
依题意 g(x)max = ∴=
解得: (舍去) 或
检验:当时,g(x)=
∵ x ∈[-1,2 ]
∴ x = 时,g(x)max = , x = -1 时= -4
符合题意。
综上得 :
-1
2
1
2
1
-1
同课章节目录
