福建省四地六校2011-2012学年高二下学期第二次月考试题数学理
文档属性
| 名称 | 福建省四地六校2011-2012学年高二下学期第二次月考试题数学理 |  | |
| 格式 | zip | ||
| 文件大小 | 135.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-20 22:04:09 | ||
图片预览




文档简介
“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考
2011-2012学年下学期第二次月考
高二数学(理科)试题
(考试时间:120分钟 总分:150分)
一、选择题(本题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项
是符合题目要求的。)
1.设复数的共轭复数是,且=2+i,则在复平面内所对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.“所有6的倍数都是3的倍数,某数m是6的倍数,则m是3的倍数。”上述推理是( )
A.正确的 B.结论错误 C.小前提错误 D.大前提错误
3.曲线与直线所围成的图形的面积为( )
A. B.
C. D.
4.二项式的展开式中的系数为 ( )
A.40 B.20 C.10 D.5
5.函数的单调递减区间是 ( )
A.(–1, 2) B.(–∞, –1)与(1, +∞)
C.(–∞, –2)与(0, +∞) D.(–2,0)
6.“函数在一点的导数值为0”是“函数在这点取极值”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.,则 的值为( )
A.0 B.-1 C.1 D.
8.某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有( )
A.个 B.个
C.个 D.个
9. 对一切实数x,不等式恒成立,则实数a的取值范围是( )
A.(-∞,-2] B.[-2,2] C.[-2,+∞) D.[0,+∞)
10.已知二次函数的导数为,,对于任意实数都有,则的最小值为( )
A. B. C. D.
二、填空题(本题共5小题,每小题4分,共20分)
11.用数学归纳法证明1+2+…+(2n+1)=(n+1)(2n+1)时,从到,左边需要增加的代数式是
12.函数的图象与直线相切于点(1,-1)处,则的值是
13. 定义在上的可导函数,已知的图象如图所示,
则的增区间是 .
14.已知函数在区间上的极大值与极小值分别为,则
15.对于命题:,则;将它类比到平面的情形是:,有;将它类比到空间的情形应该是:若O是四面体ABCD内一点,则有___________。
三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)
16.(本题满分13分)
已知的展开式的系数和大992。
求在的展开式中:
(1)常数项(用数字表示);(2)二项式系数最大的项。
17.(本题满分13分)
4位男生和4位女生共8位同学站成一排,计算下列情况:
(1)男生甲和女生乙相邻排队的概率;
(2)男生甲和女生乙顺序固定的概率;
(3)男生甲不站左端且女生乙不站右端队的排法有几种.
18.(本题满分13分)
已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线相交于不同的两点M、N.当时,
求的取值范围.
19.(本题满分13分)
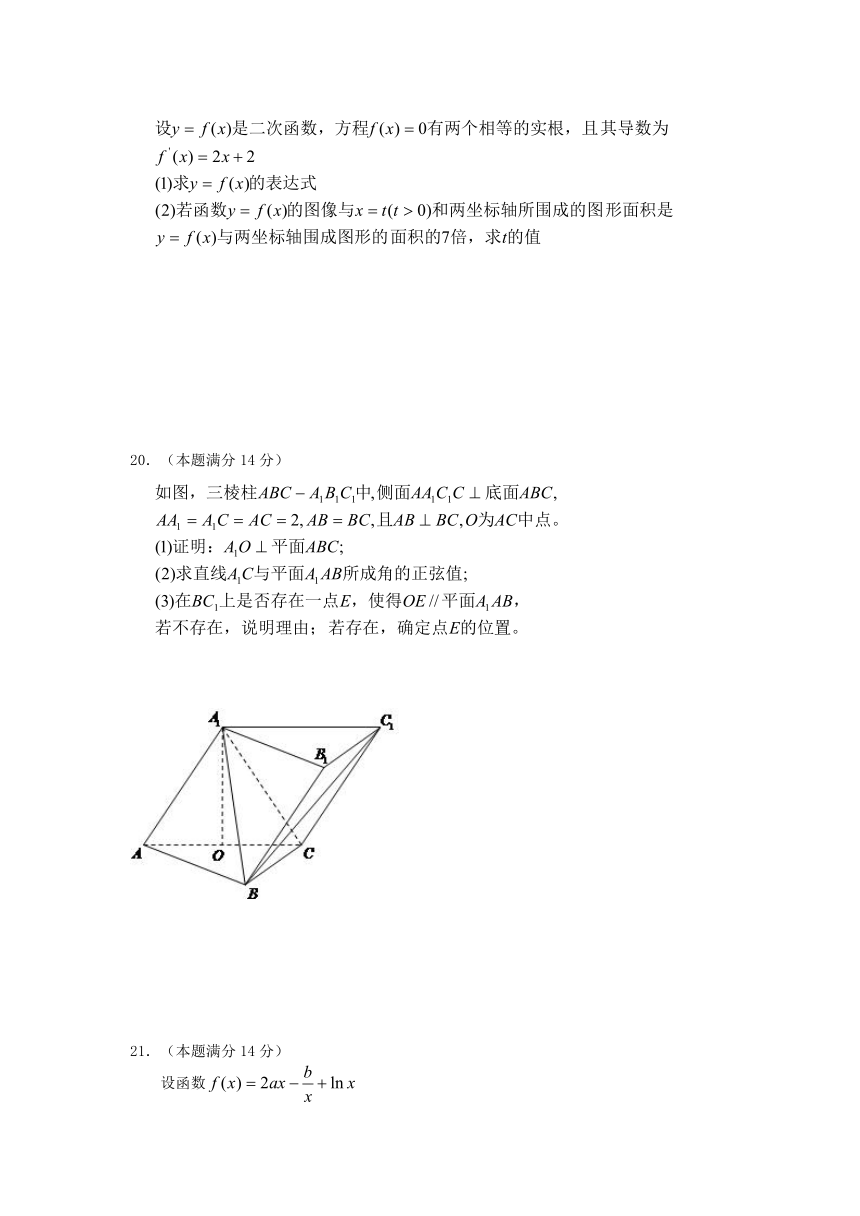
20.(本题满分14分)
21.(本题满分14分)
设函数
⑴若,
①求的值;
②
⑵当上是单调递增函数,求的取值范围。
(参考数据)
“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考
2011-2012学年下学期第二次月考
高二数学(理科)参考答案
一、选择题
1.D 2.A 3.C 4.C 5.D 6.D 7.C 8.A 9.C 10.C 二、填空题
11.(2k+2)(2k+3) 12.-1 13.(-∞,+∞) (或R) 14.32
15.
三、解答题
17.解:(1)将甲、乙看成一个元素,考虑其顺序,有2种情况,
将甲乙与其他人进行全排列,共7个元素,有A77=5040种情况,
共有2×5040=10080种情况;
所以概率为0.25.......................................4分
(2)先对8个人全排列,有A88=40320种情况,
其中甲乙的顺序有两种情况,即甲在乙前或甲在乙后,数目各占一半,
则甲、乙顺序一定的情况有×40320=20160种情况,
所以概率为0.5...................................................8分
(3)①男生甲站右端则有A77=5040种站法
②男生甲不站右端则有6种选择,而女生乙也有6种选择,剩下6人有A66
=720种排法,则有6×6×720=25920种
所以共有5040+25920=30960种........................13分
18.解(1)依题意可设椭圆方程为 ,则右焦点F()
由题设 解得 故所求椭圆的方程为.......6分
(2)设P为弦MN的中点,由 得
设 ....................................................7分
由于直线与椭圆有两个交点,即 ①
从而
又,则
即 ② ........................................ 10分
把②代入①得 解得
由②得 解得
故所求m的取范围是() .................................... 13分
19.解:(1)设函数----------------1分
依题意得----------3分
解得:-------------------6分
-------------------7分
(2)如图(图略)
(2)如图,以O为原点,所在直线分别为x,y,z轴建立空间直角坐标系.
由题意可知,
所以得:
则有:
设平面的一个法向量为,则有
,
令y=1,得 所以.
.
.......9分
即,得
所以得
,
即,得
即存在这样的点E,E为的中点.........................................14
21.⑴①,
。
处取得极值,
..........................3分
②在,
,
;
;
;
.,
,
又
,
..........9分
..............................14分
2011-2012学年下学期第二次月考
高二数学(理科)试题
(考试时间:120分钟 总分:150分)
一、选择题(本题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项
是符合题目要求的。)
1.设复数的共轭复数是,且=2+i,则在复平面内所对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.“所有6的倍数都是3的倍数,某数m是6的倍数,则m是3的倍数。”上述推理是( )
A.正确的 B.结论错误 C.小前提错误 D.大前提错误
3.曲线与直线所围成的图形的面积为( )
A. B.
C. D.
4.二项式的展开式中的系数为 ( )
A.40 B.20 C.10 D.5
5.函数的单调递减区间是 ( )
A.(–1, 2) B.(–∞, –1)与(1, +∞)
C.(–∞, –2)与(0, +∞) D.(–2,0)
6.“函数在一点的导数值为0”是“函数在这点取极值”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
7.,则 的值为( )
A.0 B.-1 C.1 D.
8.某城市的汽车牌照号码由2个英文字母后接4个数字组成,其中4个数字互不相同的牌照号码共有( )
A.个 B.个
C.个 D.个
9. 对一切实数x,不等式恒成立,则实数a的取值范围是( )
A.(-∞,-2] B.[-2,2] C.[-2,+∞) D.[0,+∞)
10.已知二次函数的导数为,,对于任意实数都有,则的最小值为( )
A. B. C. D.
二、填空题(本题共5小题,每小题4分,共20分)
11.用数学归纳法证明1+2+…+(2n+1)=(n+1)(2n+1)时,从到,左边需要增加的代数式是
12.函数的图象与直线相切于点(1,-1)处,则的值是
13. 定义在上的可导函数,已知的图象如图所示,
则的增区间是 .
14.已知函数在区间上的极大值与极小值分别为,则
15.对于命题:,则;将它类比到平面的情形是:,有;将它类比到空间的情形应该是:若O是四面体ABCD内一点,则有___________。
三、解答题(本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.)
16.(本题满分13分)
已知的展开式的系数和大992。
求在的展开式中:
(1)常数项(用数字表示);(2)二项式系数最大的项。
17.(本题满分13分)
4位男生和4位女生共8位同学站成一排,计算下列情况:
(1)男生甲和女生乙相邻排队的概率;
(2)男生甲和女生乙顺序固定的概率;
(3)男生甲不站左端且女生乙不站右端队的排法有几种.
18.(本题满分13分)
已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线
的距离为3.
(1)求椭圆的方程;
(2)设椭圆与直线相交于不同的两点M、N.当时,
求的取值范围.
19.(本题满分13分)
20.(本题满分14分)
21.(本题满分14分)
设函数
⑴若,
①求的值;
②
⑵当上是单调递增函数,求的取值范围。
(参考数据)
“华安、连城、永安、漳平一中、龙海二中、泉港一中”六校联考
2011-2012学年下学期第二次月考
高二数学(理科)参考答案
一、选择题
1.D 2.A 3.C 4.C 5.D 6.D 7.C 8.A 9.C 10.C 二、填空题
11.(2k+2)(2k+3) 12.-1 13.(-∞,+∞) (或R) 14.32
15.
三、解答题
17.解:(1)将甲、乙看成一个元素,考虑其顺序,有2种情况,
将甲乙与其他人进行全排列,共7个元素,有A77=5040种情况,
共有2×5040=10080种情况;
所以概率为0.25.......................................4分
(2)先对8个人全排列,有A88=40320种情况,
其中甲乙的顺序有两种情况,即甲在乙前或甲在乙后,数目各占一半,
则甲、乙顺序一定的情况有×40320=20160种情况,
所以概率为0.5...................................................8分
(3)①男生甲站右端则有A77=5040种站法
②男生甲不站右端则有6种选择,而女生乙也有6种选择,剩下6人有A66
=720种排法,则有6×6×720=25920种
所以共有5040+25920=30960种........................13分
18.解(1)依题意可设椭圆方程为 ,则右焦点F()
由题设 解得 故所求椭圆的方程为.......6分
(2)设P为弦MN的中点,由 得
设 ....................................................7分
由于直线与椭圆有两个交点,即 ①
从而
又,则
即 ② ........................................ 10分
把②代入①得 解得
由②得 解得
故所求m的取范围是() .................................... 13分
19.解:(1)设函数----------------1分
依题意得----------3分
解得:-------------------6分
-------------------7分
(2)如图(图略)
(2)如图,以O为原点,所在直线分别为x,y,z轴建立空间直角坐标系.
由题意可知,
所以得:
则有:
设平面的一个法向量为,则有
,
令y=1,得 所以.
.
.......9分
即,得
所以得
,
即,得
即存在这样的点E,E为的中点.........................................14
21.⑴①,
。
处取得极值,
..........................3分
②在,
,
;
;
;
.,
,
又
,
..........9分
..............................14分
同课章节目录
