根与系数的关系课件
图片预览



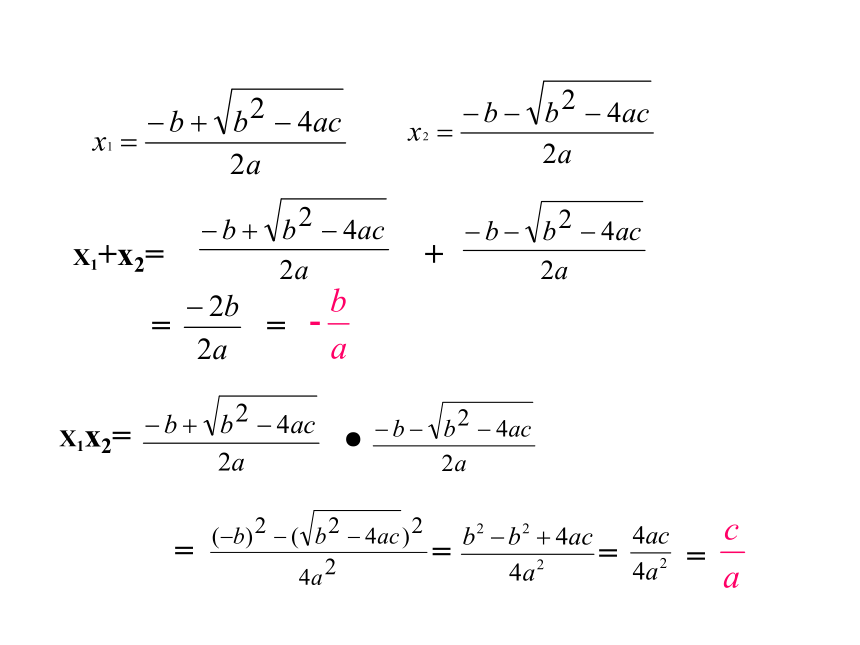

文档简介
(共15张PPT)
根与系数的关系
面对生活上的困难,我们要以积极、乐观的心态去面对.
面对学习上的困难,我们要勇于探索解决问题的方法。
接庄中学 王金凤
喜羊羊和灰太狼
一天小灰灰拿着两道题问灰太狼,灰太狼不会。于是他想办法抓到了喜羊羊。他告诉喜羊羊,如果喜羊羊教会了小灰灰,他就把喜羊羊放了!否则就把它吃掉!题目如下:
不解方程,也不代入检验,判断下列方程后面括号里的两个数是不是它的根。
(1)x2-5x+4=0 (1 , 4)
(2)3x2+5x-2=0 ( , 2)
喜羊羊一看,很快说出了答案,并且答应教会小灰灰做题的方法!
请回答:
一元二次方程的一般形式
一元二次方程的求根公式
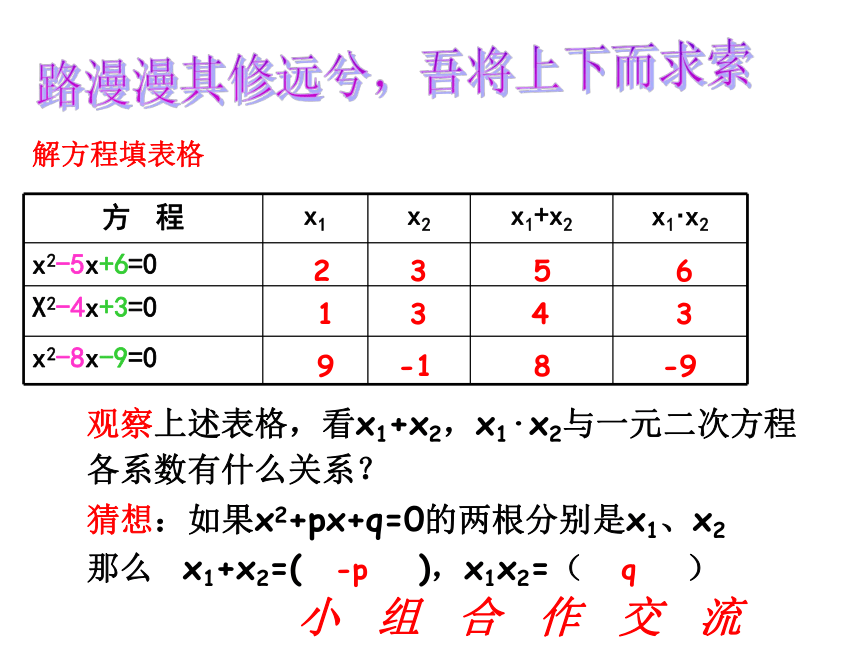
方 程 x1 x2 x1+x2 x1·x2
x2-5x+6=0
X2-4x+3=0
x2-8x-9=0
解方程填表格
观察上述表格,看x1+x2,x1·x2与一元二次方程各系数有什么关系?
猜想:如果x2+px+q=0的两根分别是x1、x2
那么 x1+x2=( ),x1x2=( )
小 组 合 作 交 流
2
3
5
6
1
3
4
3
9
8
-9
-1
-p
q
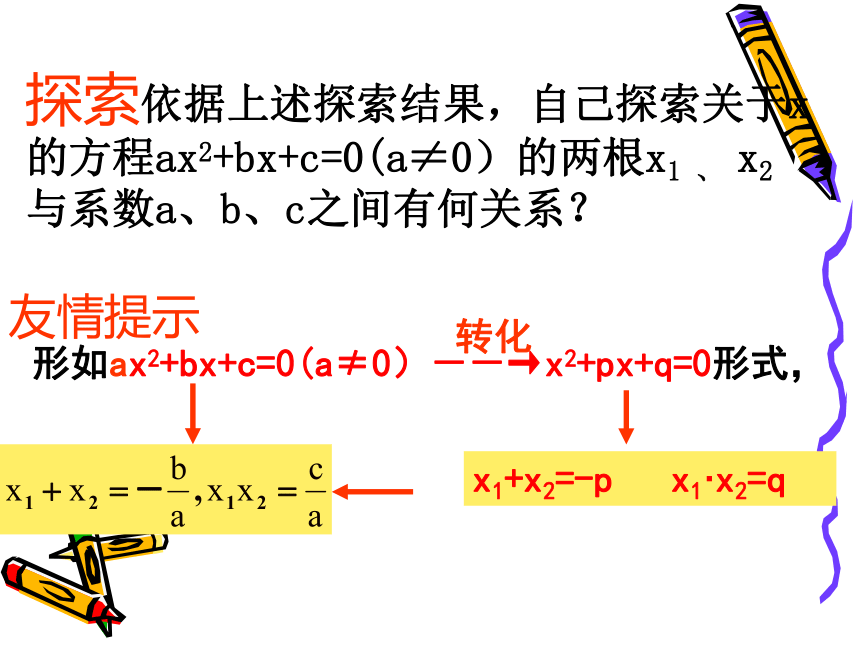
探索依据上述探索结果,自己探索关于x的方程ax2+bx+c=0(a≠0)的两根x1 、 x2与系数a、b、c之间有何关系?
友情提示
形如ax2+bx+c=0(a≠0)--→x2+px+q=0形式,
转化
x1+x2=-p x1·x2=q
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
=
一元二次方程根与系数的关系
推论1
条件:
(1)a ≠ 0
(2)b2-4ac≥0
练习:已知下列方程的两个根是x1、x2,不解方程,写出下列方程的两根和与两根积:
(1)2x2-9x=-5 (2)x2-3x+1=0
(3)4x2-7x=1 (4)2x2+3x=0
注意:(1)化成一般形式,定a、b、c
(2)直接用根与系数的关系
结论 中,共有几个量?本题已知几个量?可以先求哪一个未知的量?
已知关于x的方程3x2-4x+2m-1=0的一个根为 ,求它的另一个根及m的值.
提示:一元二次方程根的的常见用法:
(1)代入方程
(2)根与系数的关系
分析:
此题中a=____,b=____,c=____
3
-4
2m-1
不解方程,也不代入检验,判断下列方程后面括号里的两个数是不是它的根。
(1)x2-5x+4=0 (1 , 4)
(2)3x2+5x-2=0 ( , 2)
(1)代入
(2)解方程
(3)根与系数的关系
是
不是
总结:验一元二次方程根的方法:
1 、 2011湖北武汉5T,3分)
已知方程x2+4x+3=0的两个根为x1,x2,则x1x2=( )
A 4 B 3 C -4 D -3
2、2011江西6T,3分
x=1是方程x2+bx-2=0的一个根,则方程的另一个根和b分别是( )
A 1 ,1 B 2 ,2 C -2 ,1 D -1,-1
3、2011广东株洲13T,3分
孔明同学在解一元二次方程x2-3x+c=0时,正确解得x1=1,x2=2,则c的值为( )
4、2011山东德州4T,4分
若x1,x2是方程x2+x-1=0的两个根,则x1+x2=( ),x1x2=( ),
x12+x22=( )
B
C
2
-1
-1
3
(a+b)2=a2+2ab+b2
a2+b2=(a+b)2-2ab
友情提示
作业:
基础必做题:
课本P65CT 7.9 1题(3)(4)
同步练习册P62基础自测1、2
选做: 同步练习册能力提升3、4
1、思考
若方程x2-3x-3=0的两根分别是x1、x2,则
x12-3x1=( ),x12-2x1+x2=( )
2、我设计 我快乐!
若一元二次方程的两根分别为3,4,写
出一个二次项系数为1的一元二次方程
3
6
x12-3x1+x1+x2
根与系数的关系
面对生活上的困难,我们要以积极、乐观的心态去面对.
面对学习上的困难,我们要勇于探索解决问题的方法。
接庄中学 王金凤
喜羊羊和灰太狼
一天小灰灰拿着两道题问灰太狼,灰太狼不会。于是他想办法抓到了喜羊羊。他告诉喜羊羊,如果喜羊羊教会了小灰灰,他就把喜羊羊放了!否则就把它吃掉!题目如下:
不解方程,也不代入检验,判断下列方程后面括号里的两个数是不是它的根。
(1)x2-5x+4=0 (1 , 4)
(2)3x2+5x-2=0 ( , 2)
喜羊羊一看,很快说出了答案,并且答应教会小灰灰做题的方法!
请回答:
一元二次方程的一般形式
一元二次方程的求根公式
方 程 x1 x2 x1+x2 x1·x2
x2-5x+6=0
X2-4x+3=0
x2-8x-9=0
解方程填表格
观察上述表格,看x1+x2,x1·x2与一元二次方程各系数有什么关系?
猜想:如果x2+px+q=0的两根分别是x1、x2
那么 x1+x2=( ),x1x2=( )
小 组 合 作 交 流
2
3
5
6
1
3
4
3
9
8
-9
-1
-p
q
探索依据上述探索结果,自己探索关于x的方程ax2+bx+c=0(a≠0)的两根x1 、 x2与系数a、b、c之间有何关系?
友情提示
形如ax2+bx+c=0(a≠0)--→x2+px+q=0形式,
转化
x1+x2=-p x1·x2=q
X1+x2=
+
=
=
-
X1x2=
●
=
=
=
=
一元二次方程根与系数的关系
推论1
条件:
(1)a ≠ 0
(2)b2-4ac≥0
练习:已知下列方程的两个根是x1、x2,不解方程,写出下列方程的两根和与两根积:
(1)2x2-9x=-5 (2)x2-3x+1=0
(3)4x2-7x=1 (4)2x2+3x=0
注意:(1)化成一般形式,定a、b、c
(2)直接用根与系数的关系
结论 中,共有几个量?本题已知几个量?可以先求哪一个未知的量?
已知关于x的方程3x2-4x+2m-1=0的一个根为 ,求它的另一个根及m的值.
提示:一元二次方程根的的常见用法:
(1)代入方程
(2)根与系数的关系
分析:
此题中a=____,b=____,c=____
3
-4
2m-1
不解方程,也不代入检验,判断下列方程后面括号里的两个数是不是它的根。
(1)x2-5x+4=0 (1 , 4)
(2)3x2+5x-2=0 ( , 2)
(1)代入
(2)解方程
(3)根与系数的关系
是
不是
总结:验一元二次方程根的方法:
1 、 2011湖北武汉5T,3分)
已知方程x2+4x+3=0的两个根为x1,x2,则x1x2=( )
A 4 B 3 C -4 D -3
2、2011江西6T,3分
x=1是方程x2+bx-2=0的一个根,则方程的另一个根和b分别是( )
A 1 ,1 B 2 ,2 C -2 ,1 D -1,-1
3、2011广东株洲13T,3分
孔明同学在解一元二次方程x2-3x+c=0时,正确解得x1=1,x2=2,则c的值为( )
4、2011山东德州4T,4分
若x1,x2是方程x2+x-1=0的两个根,则x1+x2=( ),x1x2=( ),
x12+x22=( )
B
C
2
-1
-1
3
(a+b)2=a2+2ab+b2
a2+b2=(a+b)2-2ab
友情提示
作业:
基础必做题:
课本P65CT 7.9 1题(3)(4)
同步练习册P62基础自测1、2
选做: 同步练习册能力提升3、4
1、思考
若方程x2-3x-3=0的两根分别是x1、x2,则
x12-3x1=( ),x12-2x1+x2=( )
2、我设计 我快乐!
若一元二次方程的两根分别为3,4,写
出一个二次项系数为1的一元二次方程
3
6
x12-3x1+x1+x2
