第3章平面上直线的位置关系和度量关系复习小结课件
文档属性
| 名称 | 第3章平面上直线的位置关系和度量关系复习小结课件 |  | |
| 格式 | zip | ||
| 文件大小 | 372.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-20 22:32:58 | ||
图片预览







文档简介
(共39张PPT)
第3章
平面上两直线的位置关
系与度量关系复习小结
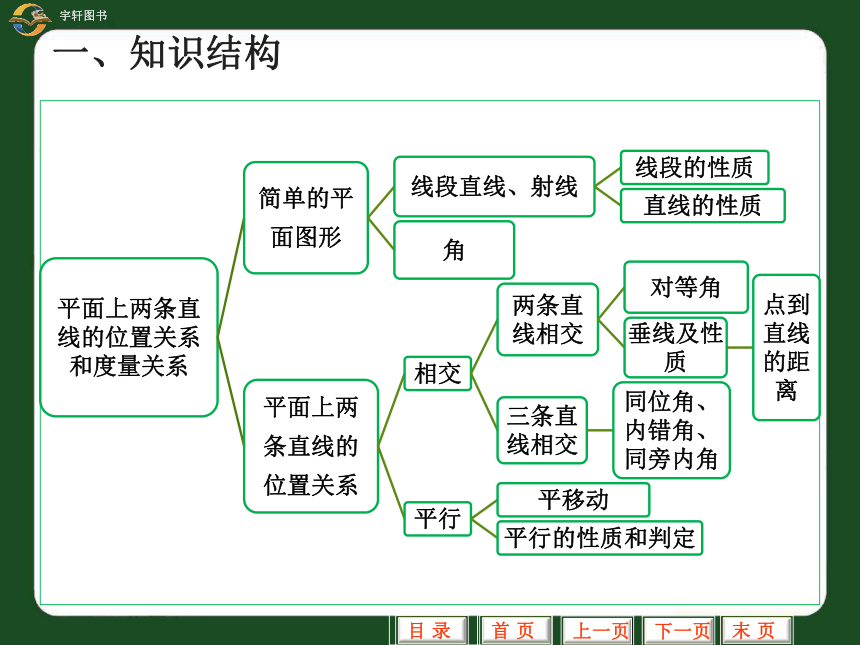
一、知识结构
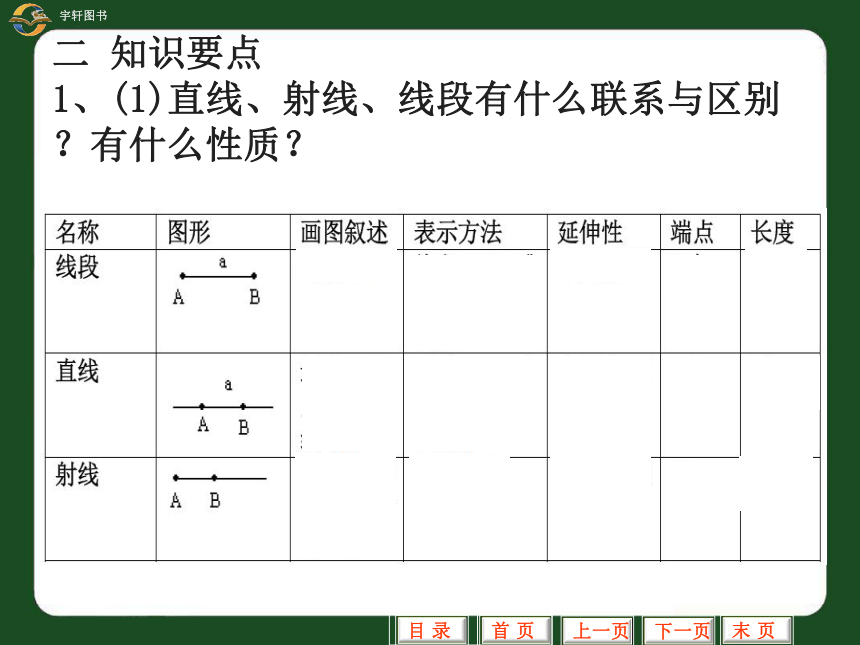
二 知识要点
1、(1)直线、射线、线段有什么联系与区别?有什么性质?
0个
1个
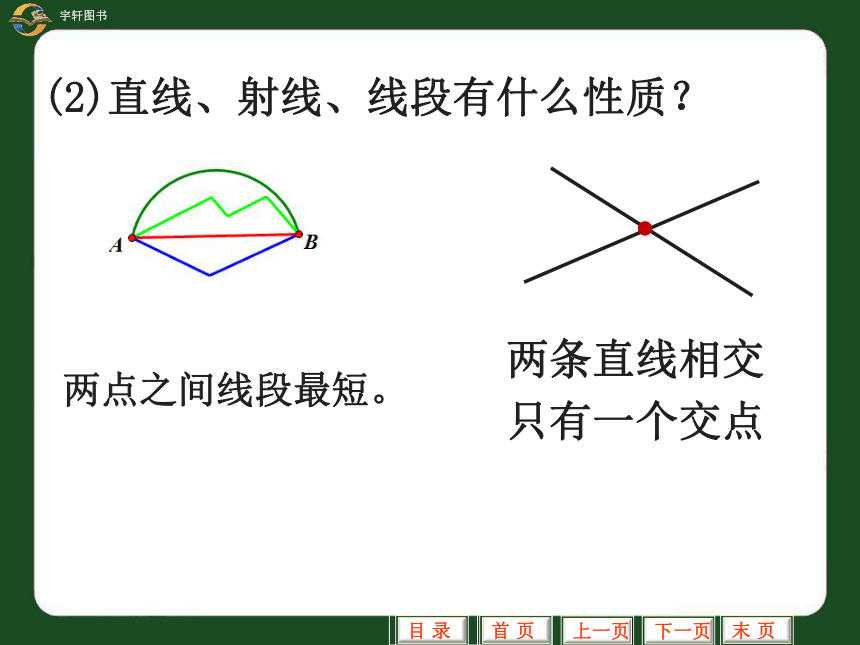
(2)直线、射线、线段有什么性质?
两条直线相交
只有一个交点
两点之间线段最短。
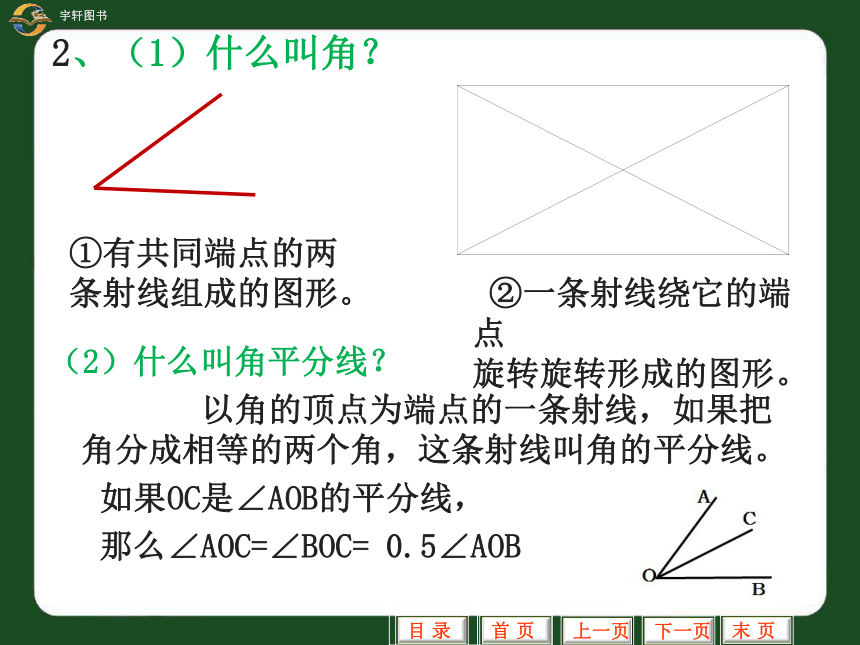
2、(1)什么叫角?
(2)什么叫角平分线?
以角的顶点为端点的一条射线,如果把角分成相等的两个角,这条射线叫角的平分线。
如果OC是∠AOB的平分线,
那么∠AOC=∠BOC= 0.5∠AOB
①有共同端点的两
条射线组成的图形。
②一条射线绕它的端点
旋转旋转形成的图形。
2、(2)角的度量有哪些单位?怎样换算?
角的度量单位有“度、分、秒”。
1°=60′=3600″,1′=60″
3、(1)什么叫平移?
定义:在平面内 ,将一个图形上所有的点沿某个方向移动相同的距离叫平移。
(2)平移有什么性质?
①平移不改变图形的 __________。可以改变图形的 位置。
② 经过平移对应点所连的线段 且________,对应角_________.
(3)平移后图形的位置由哪几个因素确定?
平移的方向与移动的距离
形状和大小
平行
相等
相等
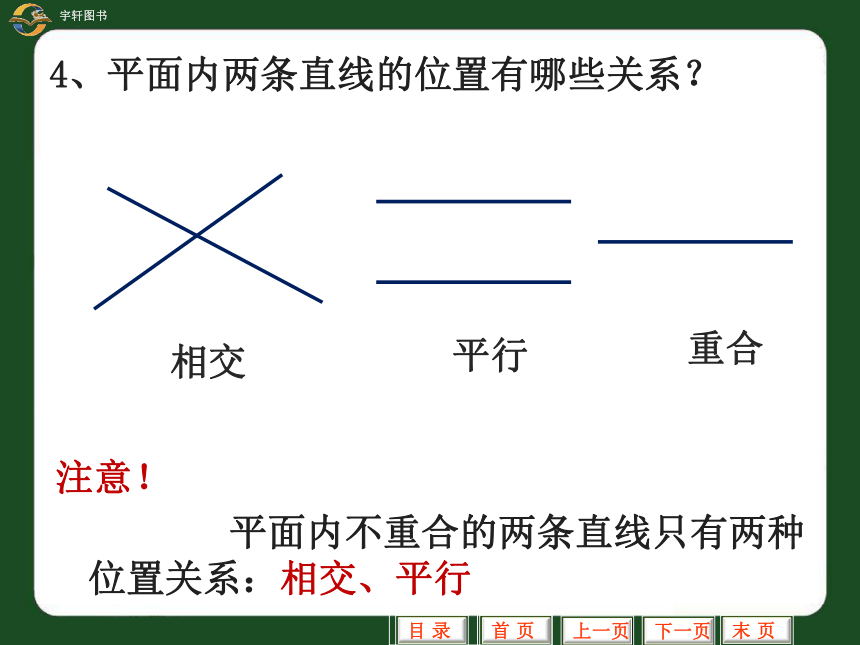
4、平面内两条直线的位置有哪些关系?
注意!
平面内不重合的两条直线只有两种位置关系:相交、平行
相交
平行
重合
5、(1)两条直线平行有哪些性质?
若a ∥b,
则:∠1= ∠6, , ∠ 4 =∠8,
∠ 2 =∠5, , ∠ 3 =∠ 7.
∠3= ∠6, , ∠ 4 =∠ 5,
∠ 4+ ∠6=180 , ∠3+ ∠5=180
两条直线平行
同位角相等
内错角相等
同旁内角互补
5、(2)怎么样判定两条直线平行?
A、利用角的关系:
①同位角相等,两直线平行,
如:若∠1= ∠6,则a ∥b
②内错角相等,两直线平行,
如:若∠3= ∠6,则a ∥b
③同旁内角互补,两直线平行。
如:若∠4+ ∠6=180 ,则a ∥b
①
5、两条直线相交形成的四个角有哪些关系?
对顶角:
如:∠1和∠3,∠2和∠4
对顶角相等。
互为补角:
如:∠1和∠2,∠3和∠4。等
6、(2)怎么样判定两条直线平行?
B、利用线的关系:
①平行于同一条直线的两条直线平行。
若a ∥c,b ∥c,则a ∥b
②同一平面内,垂直于同一条直线的两条直线平行
若b⊥a,c ⊥a,则b∥c
7、(1)什么叫互为余角 什么叫互为补角?
如果两个角的和等于直角,这两个角叫互为余角;
如图,AC ⊥BC,则∠ACD
与 ∠BCD互余。
如果两个角的和等于平角,这两个角叫互为补角。
如图, ∠ADB+ ∠ADC=180
∠ADB、 ∠ADC互补。
7、(2)互为余角、互为补角?有什么性质?
同角或等角的余角相等。同角或等角的补角相等。
如图1:若∠A+∠1=90 ,
∠1+∠2=90
则∠A=∠2
如图2:若∠A+∠D=180 ,
∠C+∠D=180
则∠A=∠C
8、(1)什么叫垂线?
当两条直线相交所构成的四个角中有一个角是直角时,就说这两条直线互相垂直,其中的一条叫做另一条的垂线。
注意!
AB⊥CD
∠AED=90
AB⊥CD
∠AED= ∠ AEC= ∠ BEC
= ∠ BED=90
8、(2)垂线有什么性质?
①过一点 直线与已知直线互相垂直。
如图,过点P可以画一条也只能
画一条直线AB垂直CD.
②连接直线外一点与直线上各点的所有线段中,垂线段最短。
如图,PE⊥CF于E,
则 PE<PD,PE∠PC, PE<PF
有且只有一条
9、距离的概念
两点间的距离
连接两点
的线段的长度.
点到直线的距离:
直线外一点到这条直线的垂线段的长度
两条平行线
间的距离:
两条平
行线中一条
上任意一点
到另一条的
距离。
二 专题研究
1、牢记概念,把握异同
【例1】判断正误
(1)延长射线OA; ( )
(2) 直线a比射线OA长,射线OA比线
段AB长; ( )
(3)线段AB的一半就是线段AB的中点, ( )
(4) 连接两点的线段叫做这两点间的距离 ( )
【解析】射线OA是朝OA方向无限延伸的,所以没有必要在OA方向延长,所以(1)错;
直线、射线是无限长的,所以直线与射线、直线、射线与线段不能比大小,所以(2)错;
中点是一个点,而不是一条线段,所以(3)错;
两点间的距离是指这两点间的线段的长度,是数量,而不是图形,所以(4)错。
×
×
×
×
【点评】
这一单元主要有三个方面的概念要
注意区别:“线段、直线、射线”,
“点与点的距离,点与直线的距离,两
平行线间的距离”,“互为余角、互为
补角”。
【变式练习一】
1、如图,∠ACB=90 ,AD∥BC,若AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是_____cm,点A、B间的距离是______cm, AD与BC间的距离是______cm.
【解】点B到AC的距离是垂线段
BC的长,等于12cm,点A、B的距离是线段AB的长,等于13cm.AD、BC的距离是公垂线段AC的长等于5cm.
12
13
5
2、下面说法中
(1)若∠1+∠2=90 ,则∠1叫∠2的补角
(2)若∠A+∠B=180 ,则∠A、∠B互为补角,
(3) 平角就是一条直线,
(4)一条线段绕着一个端点旋转形成的图形叫做角
正确的个数是( )
A 1个 B 2个 C 3个 D 4个。
【解】两个角的和等于90 ,这两个角角互为余角,所以(1)错;
(2)正确;
平角的两边在一条直线上,但平角是角,不是直线,所以(3)错,
角的两边是射线,不是线段,所以(4)错。选A
A
2、注意技巧,化难为易
【例2】如图,小于平角的角有_____个。
【解】图中的角可以按顶点分成4类,以A为顶点的有3个,以B、C、D
为顶点的各有4个,共有15个。
【点评】数线段的条数、角的个数,要注意分类或按序计数。才能做到不重复、不遗漏。
15
【变式练习二】
图中,有_____条线段,_______条直线,_______条能用字母表示的射线。
6
1
7
3、活用性质、推理有据
【例3】如图AD⊥BC,垂足为D,∠BAC=90 ,则∠B与∠CAD,∠C与∠BAD有什么关系?为什么?
【解】∠B=∠CAD,∠C=∠BAD
理由是:∵AD⊥BC(已知)
∴ ∠ADB=∠ADC=90 (垂直定义)
∴∠BAD+∠B=90 , ∠C+∠CAD=90
(三角形内角和等于180 )
∵∠BAC=90 (已知)
∴∠BAD+∠CAD=90
∴∠B=∠CAD,∠C=∠BAD.(同角或等角的余角相等)
【变式练习三】
1、(2011四川泸州)如图,∠1与∠2互补,∠3=135°,则∠4的度数是( )
A 45° B .55° C. 65° D. 75°
【解】∵∠1与∠2互补(已知)
∴a∥b(同旁内角互补,两直线平行)
∵∠5=180 -∠3=180 -135 =45
(邻补角的定义)
∴∠4=∠5=45
(两直线平行,内错角相当) 选A.
5
A
2、如图,点O在直线AB上,OD平分∠AOC,OE平分∠BOC,则OD、OE有怎样的位置关系?说明理由。
【解】OD⊥OE
理由是:∵OD平分∠AOC,OE平分∠BOC(已知)
∴∠COD=0.5∠AOC,∠COE=0.5∠BOC
(角平分线的定义)
∴∠COD+∠COE
=0.5∠AOC+0.5∠BOC
=0.5(∠AOC+∠BOC)
=0.5×180 =90
∴OD⊥OE(垂直定义)
4、两边夹击,无坚不摧
【例4】如图,DB∥FG∥EC,点A在FG上,∠ABD=60 , ∠ACE=36 ,AP平分∠BAC,求∠PAG的度数。
【分析】本题比较复杂,可以先分析条件,寻找结论,再分析结论,寻找条件。
由条件找结论:
由:DB∥FG∥EC
∠ABD=60 , ∠ACE=36
得:∠BAG=∠ABD=60 ,∠GAC=∠ACE=36 .
由结论找条件:因为∠PAG=∠BAG-∠BAP,可以考虑先求出∠BAG和∠BAP.
4、两边夹击,无坚不摧
【例4】如图,DB∥FG∥EC,点A在FG上,∠ABD=60 , ∠ACE=36 ,AP平分∠BAC,求∠PAG的度数。
【解】∵DB∥FG∥EC,∠ABD=60 , ∠ACE=36
∴∠BAG=∠ABD=60 ,
∠GAC=∠ACE=36 .
(两直线平行,内错角相等)
∴∠BAC=∠BAG+ ∠ CAG=60 +36 =96
∵PA平分∠BAC(已知)
∴∠BAP=∠PAC=0.5∠BAC=0.5×96 =48
(角平分线定义)
∴∠PAG=∠BAG-∠BAP=60 -48 =12
【点评】
很多的 问题,通过由条件找结论,问
题得到解决,如果不能解决,再由结论找条
件,两个方向夹击,再难的问题,也难攻破
。
【变式练习四】
如图,已知AD∥BC,AB∥DF, ∠B=60 , ∠EDA=50 ,求∠CDF的度数。
【解】∵AB∥DF, ∠B=60 (已知)
∴∠DFC=∠B=60
( )
∵AD∥BC(已知)
∴∠ADF=∠DFC=60 ( )
∵ ∠CDF+∠ADF+∠EDA=180
∴ ∠CDF=180 - ∠ EDA-∠ADF
=180 -60 -50 =70
两直线平行,同位角相等
两直线平行,内错角相等
5、添加辅助线、柳暗花明又一村
【例5】若AB∥CD,∠ABE=120 ,∠DCE=35 ,求∠BEC的度数
【解】作EF∥AB, 又∵AB∥CD(已知),∴AB∥EF∥CD
(两条直线都平行于第三条直线,
那么这两条直线互相平行)
∴∠B+∠BEF=180
(两直线平行,同旁内角互补),
∠C=∠CEF=35 (两直线平行,内错角相等)
∴∠BEF=180 -∠B=180 -120 =60
∴∠BEC=∠BEF+∠CEF=60 +35 =95
F
【变式练习】
(2011新疆乌鲁木齐)如图,AD与BC相交于点O,AB∥CD,若∠B=30°,∠D=60°.则∠AOC= 度.
【解】作OE∥AB,
∵AB∥CD(已知)
∴OE∥CD
则∠D=∠AOE=60 ,
∠C=∠COE=30
(两直线平行,同位角相等)
∴∠AOC=∠AOE+ ∠ COE=60 +30 =90
E
课堂练习
1、如图,平移方格纸中的图形,使A点平移到A′点处,画出平移后的图形,并写上一句贴切、诙谐的解说词.
牵手
2、(2011邵阳)如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是
( )
A. 20° B. 25
C. 30° D. 70°
D
3、(2011广州)已知∠ α =260,则 ∠ α的补角是______度。
154
4、(2011湖北潜江)如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23°B.16°C.20°D.26°
【解】:解:∵AB∥EF∥CD,
∠ABC=46°,∠CEF=154°,
∴∠BCD=∠ABC=46°,
∠FEC+∠ECD=180°,
∴∠ECD=180°—∠FEC=26°,
∴∠BCE=∠BCD—∠ECD=46°—26°=20°.
5、(2010南通)如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D,C两点分别落在D’,C’的位置,并利用量角器量得∠EFB=65 ,则∠AED’等于_____度。
【解】因为AD∥BC(已知)
∴∠DEF=∠EFB=65
(两直线平行,内错角相等)
∵∠DEF=∠D’EF=65
∴∠AED’=180 -∠D’EF-∠DEF
=180 -65 -65 =50
6、如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20 ,求∠AOM和∠NOC的度数。
【解】∵OE平分∠BON,
∠EON=20 (已知)
∴ ∠BON=2 ∠EON=2 ×20 =40
∴ ∠ NOC=180 -∠BON=180 -40 =140
∠MOC= ∠BON=40 ,
∵OA ⊥BC,
∴ ∠AOC=90
∴ ∠AOM=90 - ∠MOC=90 -40 =50
作业:P 79复习题
第3章
平面上两直线的位置关
系与度量关系复习小结
一、知识结构
二 知识要点
1、(1)直线、射线、线段有什么联系与区别?有什么性质?
0个
1个
(2)直线、射线、线段有什么性质?
两条直线相交
只有一个交点
两点之间线段最短。
2、(1)什么叫角?
(2)什么叫角平分线?
以角的顶点为端点的一条射线,如果把角分成相等的两个角,这条射线叫角的平分线。
如果OC是∠AOB的平分线,
那么∠AOC=∠BOC= 0.5∠AOB
①有共同端点的两
条射线组成的图形。
②一条射线绕它的端点
旋转旋转形成的图形。
2、(2)角的度量有哪些单位?怎样换算?
角的度量单位有“度、分、秒”。
1°=60′=3600″,1′=60″
3、(1)什么叫平移?
定义:在平面内 ,将一个图形上所有的点沿某个方向移动相同的距离叫平移。
(2)平移有什么性质?
①平移不改变图形的 __________。可以改变图形的 位置。
② 经过平移对应点所连的线段 且________,对应角_________.
(3)平移后图形的位置由哪几个因素确定?
平移的方向与移动的距离
形状和大小
平行
相等
相等
4、平面内两条直线的位置有哪些关系?
注意!
平面内不重合的两条直线只有两种位置关系:相交、平行
相交
平行
重合
5、(1)两条直线平行有哪些性质?
若a ∥b,
则:∠1= ∠6, , ∠ 4 =∠8,
∠ 2 =∠5, , ∠ 3 =∠ 7.
∠3= ∠6, , ∠ 4 =∠ 5,
∠ 4+ ∠6=180 , ∠3+ ∠5=180
两条直线平行
同位角相等
内错角相等
同旁内角互补
5、(2)怎么样判定两条直线平行?
A、利用角的关系:
①同位角相等,两直线平行,
如:若∠1= ∠6,则a ∥b
②内错角相等,两直线平行,
如:若∠3= ∠6,则a ∥b
③同旁内角互补,两直线平行。
如:若∠4+ ∠6=180 ,则a ∥b
①
5、两条直线相交形成的四个角有哪些关系?
对顶角:
如:∠1和∠3,∠2和∠4
对顶角相等。
互为补角:
如:∠1和∠2,∠3和∠4。等
6、(2)怎么样判定两条直线平行?
B、利用线的关系:
①平行于同一条直线的两条直线平行。
若a ∥c,b ∥c,则a ∥b
②同一平面内,垂直于同一条直线的两条直线平行
若b⊥a,c ⊥a,则b∥c
7、(1)什么叫互为余角 什么叫互为补角?
如果两个角的和等于直角,这两个角叫互为余角;
如图,AC ⊥BC,则∠ACD
与 ∠BCD互余。
如果两个角的和等于平角,这两个角叫互为补角。
如图, ∠ADB+ ∠ADC=180
∠ADB、 ∠ADC互补。
7、(2)互为余角、互为补角?有什么性质?
同角或等角的余角相等。同角或等角的补角相等。
如图1:若∠A+∠1=90 ,
∠1+∠2=90
则∠A=∠2
如图2:若∠A+∠D=180 ,
∠C+∠D=180
则∠A=∠C
8、(1)什么叫垂线?
当两条直线相交所构成的四个角中有一个角是直角时,就说这两条直线互相垂直,其中的一条叫做另一条的垂线。
注意!
AB⊥CD
∠AED=90
AB⊥CD
∠AED= ∠ AEC= ∠ BEC
= ∠ BED=90
8、(2)垂线有什么性质?
①过一点 直线与已知直线互相垂直。
如图,过点P可以画一条也只能
画一条直线AB垂直CD.
②连接直线外一点与直线上各点的所有线段中,垂线段最短。
如图,PE⊥CF于E,
则 PE<PD,PE∠PC, PE<PF
有且只有一条
9、距离的概念
两点间的距离
连接两点
的线段的长度.
点到直线的距离:
直线外一点到这条直线的垂线段的长度
两条平行线
间的距离:
两条平
行线中一条
上任意一点
到另一条的
距离。
二 专题研究
1、牢记概念,把握异同
【例1】判断正误
(1)延长射线OA; ( )
(2) 直线a比射线OA长,射线OA比线
段AB长; ( )
(3)线段AB的一半就是线段AB的中点, ( )
(4) 连接两点的线段叫做这两点间的距离 ( )
【解析】射线OA是朝OA方向无限延伸的,所以没有必要在OA方向延长,所以(1)错;
直线、射线是无限长的,所以直线与射线、直线、射线与线段不能比大小,所以(2)错;
中点是一个点,而不是一条线段,所以(3)错;
两点间的距离是指这两点间的线段的长度,是数量,而不是图形,所以(4)错。
×
×
×
×
【点评】
这一单元主要有三个方面的概念要
注意区别:“线段、直线、射线”,
“点与点的距离,点与直线的距离,两
平行线间的距离”,“互为余角、互为
补角”。
【变式练习一】
1、如图,∠ACB=90 ,AD∥BC,若AC=5cm,BC=12cm,AB=13cm,则点B到AC的距离是_____cm,点A、B间的距离是______cm, AD与BC间的距离是______cm.
【解】点B到AC的距离是垂线段
BC的长,等于12cm,点A、B的距离是线段AB的长,等于13cm.AD、BC的距离是公垂线段AC的长等于5cm.
12
13
5
2、下面说法中
(1)若∠1+∠2=90 ,则∠1叫∠2的补角
(2)若∠A+∠B=180 ,则∠A、∠B互为补角,
(3) 平角就是一条直线,
(4)一条线段绕着一个端点旋转形成的图形叫做角
正确的个数是( )
A 1个 B 2个 C 3个 D 4个。
【解】两个角的和等于90 ,这两个角角互为余角,所以(1)错;
(2)正确;
平角的两边在一条直线上,但平角是角,不是直线,所以(3)错,
角的两边是射线,不是线段,所以(4)错。选A
A
2、注意技巧,化难为易
【例2】如图,小于平角的角有_____个。
【解】图中的角可以按顶点分成4类,以A为顶点的有3个,以B、C、D
为顶点的各有4个,共有15个。
【点评】数线段的条数、角的个数,要注意分类或按序计数。才能做到不重复、不遗漏。
15
【变式练习二】
图中,有_____条线段,_______条直线,_______条能用字母表示的射线。
6
1
7
3、活用性质、推理有据
【例3】如图AD⊥BC,垂足为D,∠BAC=90 ,则∠B与∠CAD,∠C与∠BAD有什么关系?为什么?
【解】∠B=∠CAD,∠C=∠BAD
理由是:∵AD⊥BC(已知)
∴ ∠ADB=∠ADC=90 (垂直定义)
∴∠BAD+∠B=90 , ∠C+∠CAD=90
(三角形内角和等于180 )
∵∠BAC=90 (已知)
∴∠BAD+∠CAD=90
∴∠B=∠CAD,∠C=∠BAD.(同角或等角的余角相等)
【变式练习三】
1、(2011四川泸州)如图,∠1与∠2互补,∠3=135°,则∠4的度数是( )
A 45° B .55° C. 65° D. 75°
【解】∵∠1与∠2互补(已知)
∴a∥b(同旁内角互补,两直线平行)
∵∠5=180 -∠3=180 -135 =45
(邻补角的定义)
∴∠4=∠5=45
(两直线平行,内错角相当) 选A.
5
A
2、如图,点O在直线AB上,OD平分∠AOC,OE平分∠BOC,则OD、OE有怎样的位置关系?说明理由。
【解】OD⊥OE
理由是:∵OD平分∠AOC,OE平分∠BOC(已知)
∴∠COD=0.5∠AOC,∠COE=0.5∠BOC
(角平分线的定义)
∴∠COD+∠COE
=0.5∠AOC+0.5∠BOC
=0.5(∠AOC+∠BOC)
=0.5×180 =90
∴OD⊥OE(垂直定义)
4、两边夹击,无坚不摧
【例4】如图,DB∥FG∥EC,点A在FG上,∠ABD=60 , ∠ACE=36 ,AP平分∠BAC,求∠PAG的度数。
【分析】本题比较复杂,可以先分析条件,寻找结论,再分析结论,寻找条件。
由条件找结论:
由:DB∥FG∥EC
∠ABD=60 , ∠ACE=36
得:∠BAG=∠ABD=60 ,∠GAC=∠ACE=36 .
由结论找条件:因为∠PAG=∠BAG-∠BAP,可以考虑先求出∠BAG和∠BAP.
4、两边夹击,无坚不摧
【例4】如图,DB∥FG∥EC,点A在FG上,∠ABD=60 , ∠ACE=36 ,AP平分∠BAC,求∠PAG的度数。
【解】∵DB∥FG∥EC,∠ABD=60 , ∠ACE=36
∴∠BAG=∠ABD=60 ,
∠GAC=∠ACE=36 .
(两直线平行,内错角相等)
∴∠BAC=∠BAG+ ∠ CAG=60 +36 =96
∵PA平分∠BAC(已知)
∴∠BAP=∠PAC=0.5∠BAC=0.5×96 =48
(角平分线定义)
∴∠PAG=∠BAG-∠BAP=60 -48 =12
【点评】
很多的 问题,通过由条件找结论,问
题得到解决,如果不能解决,再由结论找条
件,两个方向夹击,再难的问题,也难攻破
。
【变式练习四】
如图,已知AD∥BC,AB∥DF, ∠B=60 , ∠EDA=50 ,求∠CDF的度数。
【解】∵AB∥DF, ∠B=60 (已知)
∴∠DFC=∠B=60
( )
∵AD∥BC(已知)
∴∠ADF=∠DFC=60 ( )
∵ ∠CDF+∠ADF+∠EDA=180
∴ ∠CDF=180 - ∠ EDA-∠ADF
=180 -60 -50 =70
两直线平行,同位角相等
两直线平行,内错角相等
5、添加辅助线、柳暗花明又一村
【例5】若AB∥CD,∠ABE=120 ,∠DCE=35 ,求∠BEC的度数
【解】作EF∥AB, 又∵AB∥CD(已知),∴AB∥EF∥CD
(两条直线都平行于第三条直线,
那么这两条直线互相平行)
∴∠B+∠BEF=180
(两直线平行,同旁内角互补),
∠C=∠CEF=35 (两直线平行,内错角相等)
∴∠BEF=180 -∠B=180 -120 =60
∴∠BEC=∠BEF+∠CEF=60 +35 =95
F
【变式练习】
(2011新疆乌鲁木齐)如图,AD与BC相交于点O,AB∥CD,若∠B=30°,∠D=60°.则∠AOC= 度.
【解】作OE∥AB,
∵AB∥CD(已知)
∴OE∥CD
则∠D=∠AOE=60 ,
∠C=∠COE=30
(两直线平行,同位角相等)
∴∠AOC=∠AOE+ ∠ COE=60 +30 =90
E
课堂练习
1、如图,平移方格纸中的图形,使A点平移到A′点处,画出平移后的图形,并写上一句贴切、诙谐的解说词.
牵手
2、(2011邵阳)如图所示,已知O是直线AB上一点,∠1=40°,OD平分∠BOC,则∠2的度数是
( )
A. 20° B. 25
C. 30° D. 70°
D
3、(2011广州)已知∠ α =260,则 ∠ α的补角是______度。
154
4、(2011湖北潜江)如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于( )
A.23°B.16°C.20°D.26°
【解】:解:∵AB∥EF∥CD,
∠ABC=46°,∠CEF=154°,
∴∠BCD=∠ABC=46°,
∠FEC+∠ECD=180°,
∴∠ECD=180°—∠FEC=26°,
∴∠BCE=∠BCD—∠ECD=46°—26°=20°.
5、(2010南通)如图,小章利用一张左、右两边已经破损的长方形纸片ABCD做折纸游戏,他将纸片沿EF折叠后,D,C两点分别落在D’,C’的位置,并利用量角器量得∠EFB=65 ,则∠AED’等于_____度。
【解】因为AD∥BC(已知)
∴∠DEF=∠EFB=65
(两直线平行,内错角相等)
∵∠DEF=∠D’EF=65
∴∠AED’=180 -∠D’EF-∠DEF
=180 -65 -65 =50
6、如图,直线BC与MN相交于点O,AO⊥BC,OE平分∠BON,若∠EON=20 ,求∠AOM和∠NOC的度数。
【解】∵OE平分∠BON,
∠EON=20 (已知)
∴ ∠BON=2 ∠EON=2 ×20 =40
∴ ∠ NOC=180 -∠BON=180 -40 =140
∠MOC= ∠BON=40 ,
∵OA ⊥BC,
∴ ∠AOC=90
∴ ∠AOM=90 - ∠MOC=90 -40 =50
作业:P 79复习题
