集合与函数概念测试题及答案(北师大版高二数学上)
文档属性
| 名称 | 集合与函数概念测试题及答案(北师大版高二数学上) | 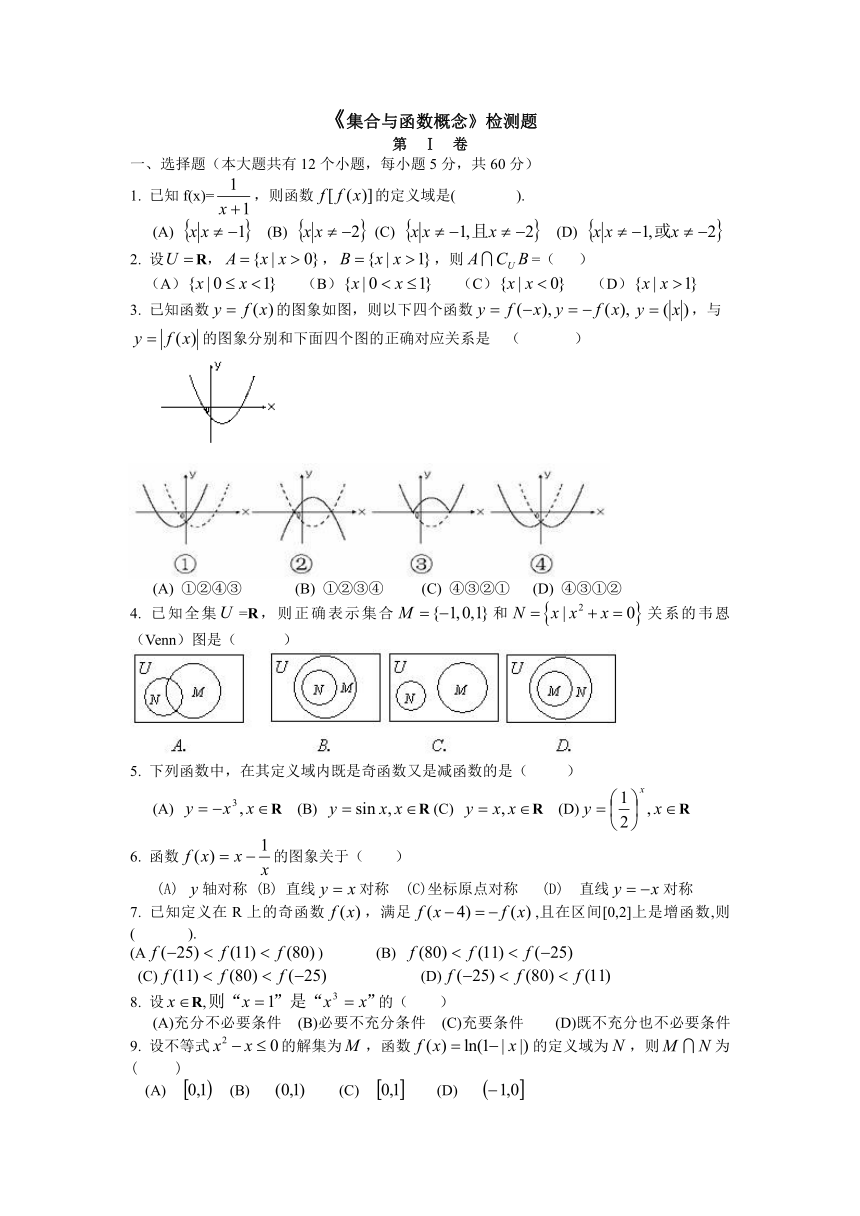 | |
| 格式 | zip | ||
| 文件大小 | 132.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-21 19:53:41 | ||
图片预览


文档简介
《集合与函数概念》检测题
第 Ⅰ 卷
一、选择题(本大题共有12个小题,每小题5分,共60分)
1. 已知f(x)=,则函数的定义域是( ).
(A) (B) (C) (D)
2. 设R,,,则=( )
(A) (B) (C) (D)
3. 已知函数的图象如图,则以下四个函数,与的图象分别和下面四个图的正确对应关系是 ( )
(A) ①②④③ (B) ①②③④ (C) ④③②① (D) ④③①②
4. 已知全集=R,则正确表示集合和关系的韦恩(Venn)图是( )
5. 下列函数中,在其定义域内既是奇函数又是减函数的是( )
(A) R (B) R (C) R (D)R
6. 函数的图象关于( )
(A) 轴对称 (B) 直线对称 (C)坐标原点对称 (D) 直线对称
7. 已知定义在R上的奇函数,满足,且在区间[0,2]上是增函数,则( ).
(A) (B)
(C) (D)
8. 设R,的( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件9. 设不等式的解集为,函数的定义域为,则为( )
(A) (B) (C) (D)
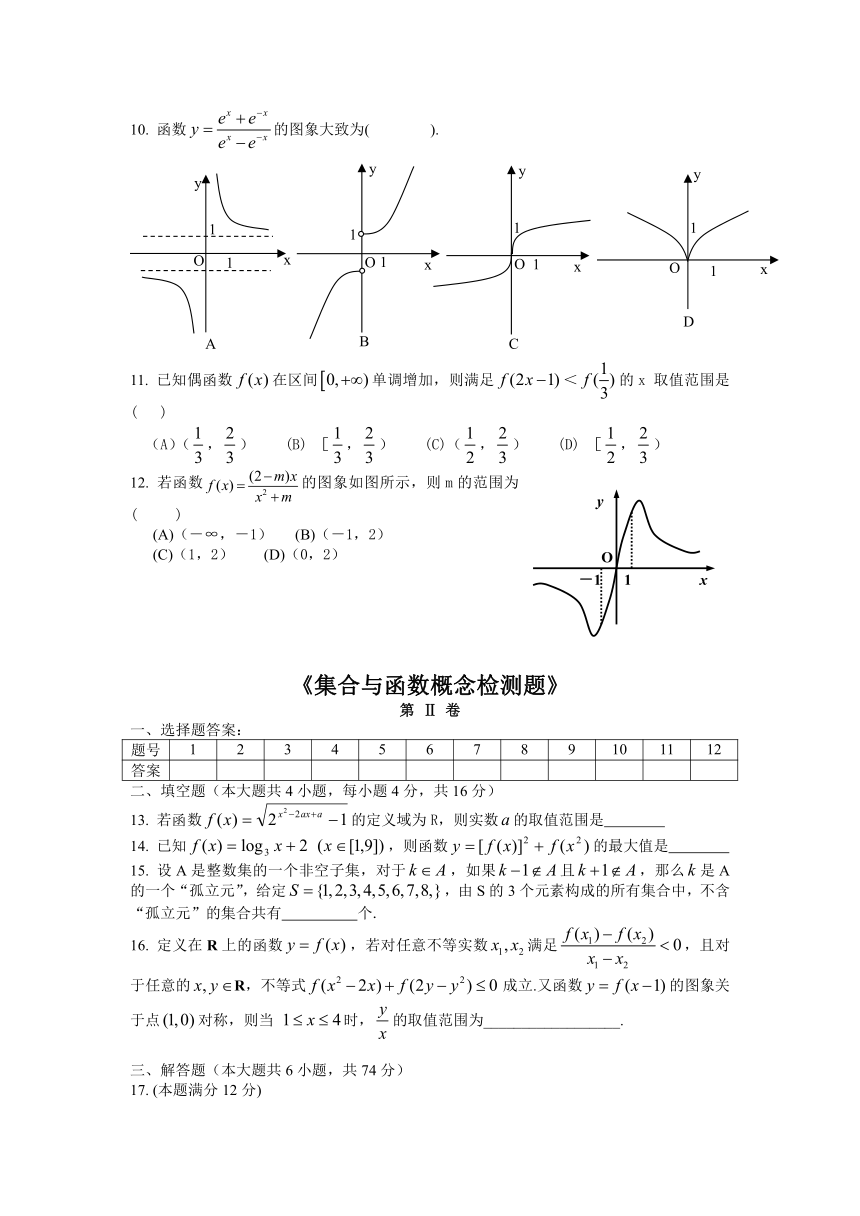
10. 函数的图象大致为( ).
11. 已知偶函数在区间单调增加,则满足<的x 取值范围是( )
(A)(,) (B) [,) (C)(,) (D) [,)
12. 若函数的图象如图所示,则m的范围为( )
(A)(-∞,-1) (B)(-1,2)
(C)(1,2) (D)(0,2)
《集合与函数概念检测题》
第 Ⅱ 卷
一、选择题答案:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4小题,每小题4分,共16分)
13. 若函数的定义域为R,则实数的取值范围是
14. 已知,则函数的最大值是
15. 设A是整数集的一个非空子集,对于,如果且,那么是A的一个“孤立元”,给定,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个.
16. 定义在R上的函数,若对任意不等实数满足,且对于任意的R,不等式成立.又函数的图象关于点对称,则当 时,的取值范围为__________________.
三、解答题(本大题共6小题,共74分)
17. (本题满分12分)
已知全集为R,,,求
18.(本题满分12分)
已知集合,且,求实数的取值范围.
19. (本小题满分12分)
若f(x)是定义在(0,+∞)上的增函数,且对一切x>0满足=f(x)-f(y),且f(6)=1, 解不等式f(x+3)-f()<2.
20. (本小题满分12分)已知函数(,常数).
(1)讨论函数的奇偶性,并说明理由;
(2)若函数在上是增函数,求实数的取值范围.
21. (本小题满分12分)已知函数(为实常数).
(1)若,作函数的图像;
(2)设在区间上的最小值为,求的表达式;
22. (本小题满分14分)
设函数,其中,R,当且仅当时,函数取得最小值
(1)求函数的表达式;
(2)若方程至少有两个不相同的实数根,求取值的集合.
《集合与函数概念》检测题参考答案
Ⅱ 卷
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B A B A C D A A A A B
二、填空题(本大题共4小题,每小题4分,共16分)
13. [0,1] 14. 13 15. 6 16.
三、解答题(本大题共6小题,共74分)
17.解:由已知得
所以 解得 所以
由得且,解得 ,
于是
.
18.解:∵,∴.
若,则,满足;
若,则.
综上,的取值范围是或,即.
19. 解:令x=y=1可得f(1)=0;反复用对应法则f(x+3)-f()=f(x2+3x).
而2=2f(6),且x>0.于是有f(x2+3x)-f(6)<f(6);即f()<f(6),
可得0<<6,解之,0<x<
不等式的解集是.
20. 解:(1)当时,,∵,∴是偶函数;
当时,,∵,
∴且,∴是非奇非偶函数.
综上,当时,是偶函数;当时,是非奇非偶函数.
(2)∵在上是增函数,∴在上恒成立,∴在上恒成立,∴.
∵当时,在上是增函数.
21. 解:(1)当时,
.作图(如右所示)
(2)当时,.
若,则在区间上是减函数,
.
若,则,图像的对称轴是直线.
当时,在区间上是减函数,.
当,即时,在区间上是增函数,.
当,即时,,
当,即时,在区间上是减函数,.
综上可得 .
22. (1)因为函数f(x)当且仅当x=-2时取得最小值-2
∴二次函数y=x2+bx+c的对称轴是x=-=-2 b=4
且有f(-2)=(-2)2-2b+c=-2 c=2
∴
(2)记方程①:2=x+a(x>0),方程②:x2+4x+2=x+a(x≤0)
分别研究方程①和方程②的根的情况:
(1)方程①有且仅有一个实数根 a<2;方程①没有实数根 a≥2
(2)方程②有且仅有两个不同的实数根,即方程x2+3x+2-a=0有两个不同的非正实数根
所以2-a≥0且△=9-4(2-a)>0 -<a≤2
方程②有且仅有一个实数根,即方程x2+3x+2-a=0有一个非正实数根
所以2-a<0或△=0,即a>2或a=-
综上可知:当方程f(x)=x+a(a∈R)有三个不同的实数根时,-<a<2
当方程f(x)=x+a(a∈R)有且仅有两个不同的实数根时,a=-或a=2
综上所述,符合题意的实数a的取值范围是[-,2]
1
x
y
1
O
A
x
y
O
1
1
B
x
y
O
1
1
C
x
y
1
1
D
O
O
x
y
1
-1
10
5
-2
3
2
1
y
x
O
-1
-3
1
10
5
-2
3
2
1
y
x
O
-1
-3
1
PAGE
第 Ⅰ 卷
一、选择题(本大题共有12个小题,每小题5分,共60分)
1. 已知f(x)=,则函数的定义域是( ).
(A) (B) (C) (D)
2. 设R,,,则=( )
(A) (B) (C) (D)
3. 已知函数的图象如图,则以下四个函数,与的图象分别和下面四个图的正确对应关系是 ( )
(A) ①②④③ (B) ①②③④ (C) ④③②① (D) ④③①②
4. 已知全集=R,则正确表示集合和关系的韦恩(Venn)图是( )
5. 下列函数中,在其定义域内既是奇函数又是减函数的是( )
(A) R (B) R (C) R (D)R
6. 函数的图象关于( )
(A) 轴对称 (B) 直线对称 (C)坐标原点对称 (D) 直线对称
7. 已知定义在R上的奇函数,满足,且在区间[0,2]上是增函数,则( ).
(A) (B)
(C) (D)
8. 设R,的( )
(A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分也不必要条件9. 设不等式的解集为,函数的定义域为,则为( )
(A) (B) (C) (D)
10. 函数的图象大致为( ).
11. 已知偶函数在区间单调增加,则满足<的x 取值范围是( )
(A)(,) (B) [,) (C)(,) (D) [,)
12. 若函数的图象如图所示,则m的范围为( )
(A)(-∞,-1) (B)(-1,2)
(C)(1,2) (D)(0,2)
《集合与函数概念检测题》
第 Ⅱ 卷
一、选择题答案:
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案
二、填空题(本大题共4小题,每小题4分,共16分)
13. 若函数的定义域为R,则实数的取值范围是
14. 已知,则函数的最大值是
15. 设A是整数集的一个非空子集,对于,如果且,那么是A的一个“孤立元”,给定,由S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个.
16. 定义在R上的函数,若对任意不等实数满足,且对于任意的R,不等式成立.又函数的图象关于点对称,则当 时,的取值范围为__________________.
三、解答题(本大题共6小题,共74分)
17. (本题满分12分)
已知全集为R,,,求
18.(本题满分12分)
已知集合,且,求实数的取值范围.
19. (本小题满分12分)
若f(x)是定义在(0,+∞)上的增函数,且对一切x>0满足=f(x)-f(y),且f(6)=1, 解不等式f(x+3)-f()<2.
20. (本小题满分12分)已知函数(,常数).
(1)讨论函数的奇偶性,并说明理由;
(2)若函数在上是增函数,求实数的取值范围.
21. (本小题满分12分)已知函数(为实常数).
(1)若,作函数的图像;
(2)设在区间上的最小值为,求的表达式;
22. (本小题满分14分)
设函数,其中,R,当且仅当时,函数取得最小值
(1)求函数的表达式;
(2)若方程至少有两个不相同的实数根,求取值的集合.
《集合与函数概念》检测题参考答案
Ⅱ 卷
题号 1 2 3 4 5 6 7 8 9 10 11 12
答案 C B A B A C D A A A A B
二、填空题(本大题共4小题,每小题4分,共16分)
13. [0,1] 14. 13 15. 6 16.
三、解答题(本大题共6小题,共74分)
17.解:由已知得
所以 解得 所以
由得且,解得 ,
于是
.
18.解:∵,∴.
若,则,满足;
若,则.
综上,的取值范围是或,即.
19. 解:令x=y=1可得f(1)=0;反复用对应法则f(x+3)-f()=f(x2+3x).
而2=2f(6),且x>0.于是有f(x2+3x)-f(6)<f(6);即f()<f(6),
可得0<<6,解之,0<x<
不等式的解集是.
20. 解:(1)当时,,∵,∴是偶函数;
当时,,∵,
∴且,∴是非奇非偶函数.
综上,当时,是偶函数;当时,是非奇非偶函数.
(2)∵在上是增函数,∴在上恒成立,∴在上恒成立,∴.
∵当时,在上是增函数.
21. 解:(1)当时,
.作图(如右所示)
(2)当时,.
若,则在区间上是减函数,
.
若,则,图像的对称轴是直线.
当时,在区间上是减函数,.
当,即时,在区间上是增函数,.
当,即时,,
当,即时,在区间上是减函数,.
综上可得 .
22. (1)因为函数f(x)当且仅当x=-2时取得最小值-2
∴二次函数y=x2+bx+c的对称轴是x=-=-2 b=4
且有f(-2)=(-2)2-2b+c=-2 c=2
∴
(2)记方程①:2=x+a(x>0),方程②:x2+4x+2=x+a(x≤0)
分别研究方程①和方程②的根的情况:
(1)方程①有且仅有一个实数根 a<2;方程①没有实数根 a≥2
(2)方程②有且仅有两个不同的实数根,即方程x2+3x+2-a=0有两个不同的非正实数根
所以2-a≥0且△=9-4(2-a)>0 -<a≤2
方程②有且仅有一个实数根,即方程x2+3x+2-a=0有一个非正实数根
所以2-a<0或△=0,即a>2或a=-
综上可知:当方程f(x)=x+a(a∈R)有三个不同的实数根时,-<a<2
当方程f(x)=x+a(a∈R)有且仅有两个不同的实数根时,a=-或a=2
综上所述,符合题意的实数a的取值范围是[-,2]
1
x
y
1
O
A
x
y
O
1
1
B
x
y
O
1
1
C
x
y
1
1
D
O
O
x
y
1
-1
10
5
-2
3
2
1
y
x
O
-1
-3
1
10
5
-2
3
2
1
y
x
O
-1
-3
1
PAGE
