人教版2021年八年级上册11.3《多边形及其内角和》同步练习(Word版含解析)
文档属性
| 名称 | 人教版2021年八年级上册11.3《多边形及其内角和》同步练习(Word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 180.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 00:00:00 | ||
图片预览




文档简介
人教版2021年八年级上册11.3《多边形及其内角和》同步练习
一.选择题
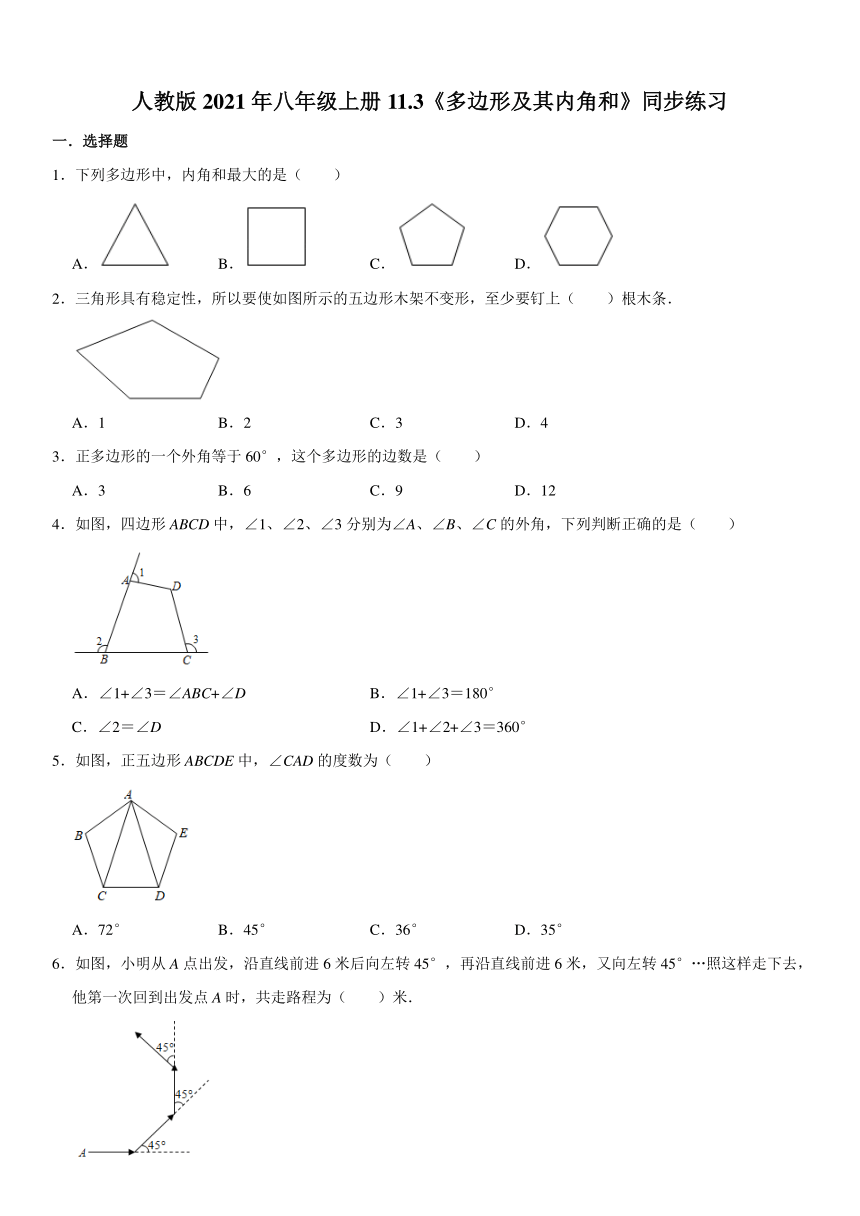
1.下列多边形中,内角和最大的是( )
A. B. C. D.
2.三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上( )根木条.
A.1 B.2 C.3 D.4
3.正多边形的一个外角等于60°,这个多边形的边数是( )
A.3 B.6 C.9 D.12
4.如图,四边形ABCD中,∠1、∠2、∠3分别为∠A、∠B、∠C的外角,下列判断正确的是( )
A.∠1+∠3=∠ABC+∠D B.∠1+∠3=180°
C.∠2=∠D D.∠1+∠2+∠3=360°
5.如图,正五边形ABCDE中,∠CAD的度数为( )
A.72° B.45° C.36° D.35°
6.如图,小明从A点出发,沿直线前进6米后向左转45°,再沿直线前进6米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )米.
A.60 B.72 C.48 D.36
7.如果一个正多边形的一个内角与一个外角的度数之比是7:2,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
8.若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )
A.14或15 B.13或14 C.13或14或15 D.14或15或16
二.填空题
9.三角形具有稳定性,要使一个四边形框架稳定不变形,至少需要钉 根木条.
10.如图,则x的值为 .
11.如果一个多边形的每个外角都是60°,那么这个多边形内角和的度数为 .
12.一个凸n边形的内角和是540°,则n= .
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
14.如图,小亮从A点出发前进2m,向右转15°,再前进2m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了 m.
15.为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是 度.
16.如图,∠A+∠B+∠C+∠D+∠E= °.
三.解答题
17.求出下列图形中x的值.
18.已知,四边形ABCD中,∠C+∠D=200°,∠B=3∠A,求∠A和∠B的度数.
19.在一个各内角都相等的多边形中,每一个内角都比与它相邻外角的3倍还大20°,求这个多边形的边数以及它的内角和.
20.如图,五角星的顶点为A、B、C、D、E,求∠A+∠B+∠C+∠D+∠E的度数?
21.观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数 3 4 5 6 … 18
∠α的度数 …
(2)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
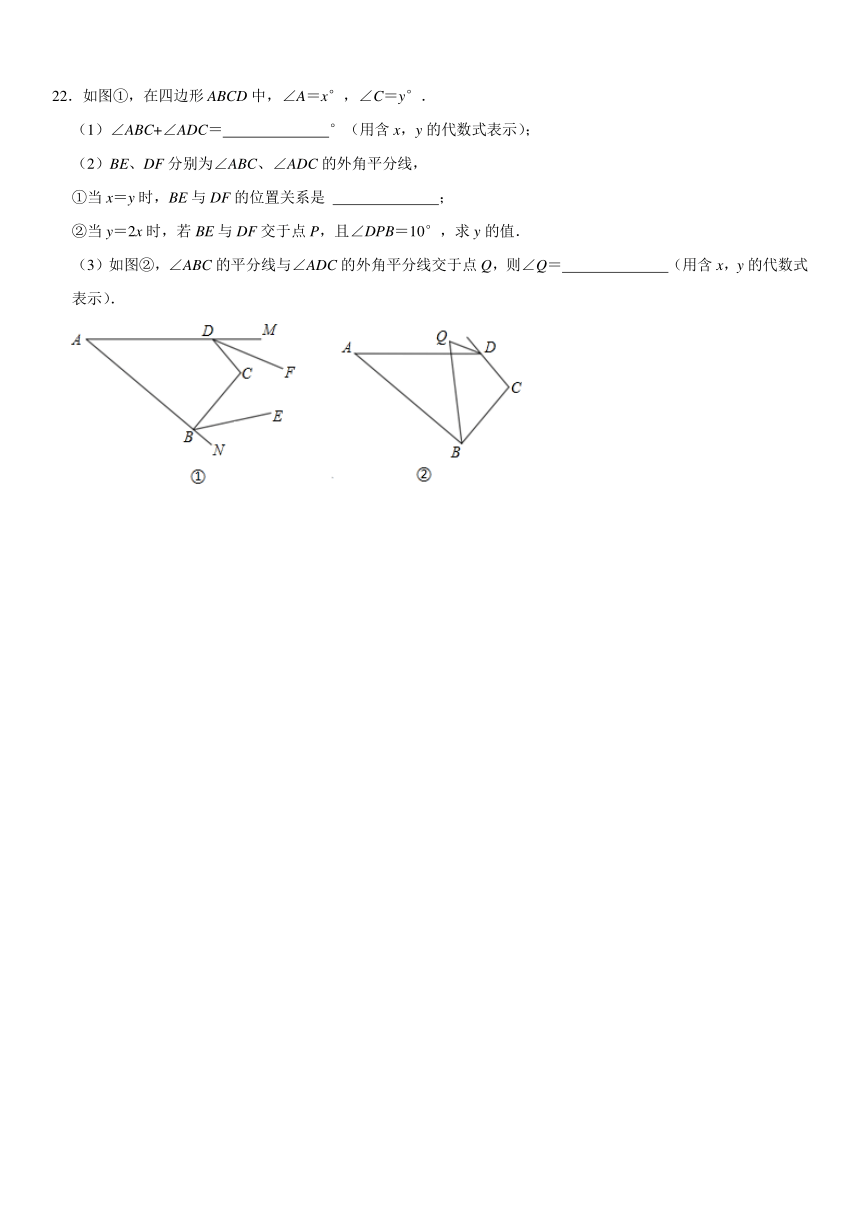
22.如图①,在四边形ABCD中,∠A=x°,∠C=y°.
(1)∠ABC+∠ADC= °(用含x,y的代数式表示);
(2)BE、DF分别为∠ABC、∠ADC的外角平分线,
①当x=y时,BE与DF的位置关系是 ;
②当y=2x时,若BE与DF交于点P,且∠DPB=10°,求y的值.
(3)如图②,∠ABC的平分线与∠ADC的外角平分线交于点Q,则∠Q= (用含x,y的代数式表示).
参考答案
一.选择题
1.解:A.三角形的内角和为180°;
B.四边形的内角和为360°;
C.五边形的内角和为:(5﹣2)×180°=540°;
D.六边形的内角和为:(6﹣2)×180°=720°;
故选:D.
2.解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.
故选:B.
3.解:∵正多边形的外角和为360°,
∴此多边形的边长为:360°÷60°=6.
故选:B.
4.解:∵∠1+∠DAB=180°,∠3+∠BCD=180°,
∴∠1+∠3+∠DAB+∠BCD=360°,
∵∠ABC+∠BCD+∠D+∠DAB=360°,
∴∠1+∠3=∠ABC+∠D,
故A符合题意;
∵∠1+∠3只有∠ABC和∠D互补时才等于180°,
故B不符合题意;
∵只有∠ABC和∠D互补时,∠2=∠D,
故C不符合题意;
∵多边形的外角和是360°,
∴∠1+∠2+∠3<360°,
故D不符合题意;
故选:A.
5.解:根据正多边形内角和公式可得,
正五边形ABCDE的内角和=180°×(5﹣2)=540°,
则∠BAE=∠B=∠E==108°,
根据正五边形的性质,△ABC≌△AED,
∴∠CAB=∠DAE=(180°﹣108°)=36°,
∴∠CAD=108°﹣36°﹣36°=36°,
故选:C.
6.解:根据题意可知,他需要转360÷45=8次才会回到原点,
所以一共走了8×6=48(米).
故选:C.
7.解:设这个正多边形的边数为n,
由题意得:(n﹣2)×180=360,
解得:n=9,
故选:C.
8.解:如图,n边形,A1A2A3…An,
若沿着直线A1A3截去一个角,所得到的多边形,比原来的多边形的边数少1,
若沿着直线A1M截去一个角,所得到的多边形,与原来的多边形的边数相等,
若沿着直线MN截去一个角,所得到的多边形,比原来的多边形的边数多1,
因此将一个多边形截去一个角后,变成十四边形,则原来的多边形的边数为13或14或15,
故选:C.
二.填空题
9.解:如图所示:
要使这个木架不变形,他至少还要再钉上1个木条,
故答案为:1
10.解:因为四边形的内角和是360°,
根据题意得,x+x+90+120=360,
解得,x=75,
故答案为:75.
11.解:∵一个多边形的每个外角都是60°,
∴n=360°÷60°=6,
则内角和为:(6﹣2)?180°=720°,
故答案为:720°.
12.解:根据题意得,
(n﹣2)?180°=540°,
解得n=5,
故答案为:5.
13.解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)
=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)
=360°﹣(90°+180°)
=90°,
故答案为:90.
14.解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为:360°÷15°=24,
则一共走了:24×2=48(m),
故答案为:48.
15.解:如图,
∵正五角星中,五边形FGHMN是正五边形,
∴∠GFN=∠FNM==108°,
∴∠AFN=∠ANF=180°﹣∠GFN=180°﹣108°=72°,
∴∠A=180°﹣∠AFN﹣∠ANF=180°﹣72°﹣72°=36°.
故答案是:36.
16.解:如图,设线段BD,BE分别与线段AC交于点N,M.
∵∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,∠DNC+∠D+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故答案为:180.
三.解答题
17.解:(1)由三角形的外角性质得,x+(x+10)=x+70,
即2x+10=x+70,
解得,x=60.
(2)根据四边形的内角和为360°得,
x+(x+10)+90+60=360,
解得,x=100.
18.解:∵四边形内角和360°,∠C+∠D=200°,
∴∠B+∠A=360°﹣200°=160°,
∵∠B=3∠A,
∴3∠A+∠A=160°,
∴∠A=40°,
∴∠B=120°.
答:∠A和∠B的度数分别是40°和120°.
19.解:设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20°)+α=180°,解得α=40°,
即多边形的每个外角为40°,
又∵多边形的外角和为360°,
∴多边形的外角个数==9,
∴多边形的边数=9,
∴多边形的内角和=(9﹣2)×180°=1260°.
20.解:如图,
由三角形的外角性质得,∠AGE=∠A+∠C,∠DFE=∠B+∠D,
∵∠AGE+∠DFE+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
21.解:(1)填表如下:
正多边形的边数 3 4 5 6 …… 18
∠α的度数 60° 45° 36° 30° …… 10°
故答案为:60°,45°,36°,30°,10°;
(2)不存在,理由如下:
假设存在n边形使得∠α=21°,得∠α=21°=()°,
解得:n=8,又n是正整数,
所以不存在正n边形使得∠α=21°.
22.解:(1)在四边形ABCD中,∠ABC+∠ADC=360°﹣∠A﹣∠DCB,
∵∠A=x°,∠DCB=y°,
∴∠ABC+∠ADC=360﹣x﹣y=(360﹣x﹣y)°,
故答案为:(360﹣x﹣y),
(2)①如图①中,
连接AC,过点C作CG∥DF,则有:
∠MDC═∠DAC+∠DCA,∠NBC═∠CAB+∠CBA,
∵BE、DF分别为∠NBC、∠MDC的角平分线,∠DAB═∠DCB═x°═y°,
∴∠FDC+∠CBE═(∠MDC+∠NBC)═(∠DAC+∠DCA+∠CAB+∠CBA)═(∠DAB+DCB)═x°,
∵CG∥DF,
∴∠FDC═∠GCD,
∵∠DCG+∠BCG═∠DCB═x°,∠FDC+∠CBE═x°,
∴∠CBE═∠BCG,
∴CG∥BE,
∴BE∥DF,
故答案为:BE∥DF.
②由(1)可知:∠ABC+∠ADC=(360﹣x﹣y)°,
∵∠ADC+∠MDC=180°,∠ABC+∠NBC=180°,
∴∠NBC+∠MDC=(x+y)°,
∵BE、DF分别为∠ABC、∠ADC的外角平分线,
∴∠PBC=∠NBC,∠PDC=∠MDC,
∴∠PBC+∠PDC=[(x+y)]°,
∵∠BCD=∠PDC+∠PBC+∠P,
∴y=10+(x+y),
即y﹣x=20,
∵y=2x,
∴x=20°,y=40°.
(3)如图②中,
由题意:∠DNQ=∠ANB=180°﹣x°﹣∠ABC,∠QDN=(180°﹣∠ADC),
∴∠Q=180°﹣∠DNQ﹣∠QDN=180°﹣(180°﹣x°﹣∠ABC)﹣(180°﹣∠ADC),
=x°+(∠ABC+∠ADC)﹣90°,
=x°+180°﹣(x+y)°﹣90°,
=[90+(x﹣y)]°,
故答案为:[90+(x﹣y)]°.
一.选择题
1.下列多边形中,内角和最大的是( )
A. B. C. D.
2.三角形具有稳定性,所以要使如图所示的五边形木架不变形,至少要钉上( )根木条.
A.1 B.2 C.3 D.4
3.正多边形的一个外角等于60°,这个多边形的边数是( )
A.3 B.6 C.9 D.12
4.如图,四边形ABCD中,∠1、∠2、∠3分别为∠A、∠B、∠C的外角,下列判断正确的是( )
A.∠1+∠3=∠ABC+∠D B.∠1+∠3=180°
C.∠2=∠D D.∠1+∠2+∠3=360°
5.如图,正五边形ABCDE中,∠CAD的度数为( )
A.72° B.45° C.36° D.35°
6.如图,小明从A点出发,沿直线前进6米后向左转45°,再沿直线前进6米,又向左转45°…照这样走下去,他第一次回到出发点A时,共走路程为( )米.
A.60 B.72 C.48 D.36
7.如果一个正多边形的一个内角与一个外角的度数之比是7:2,那么这个正多边形的边数是( )
A.11 B.10 C.9 D.8
8.若一个多边形截去一个角后,变成十四边形,则原来的多边形的边数可能为( )
A.14或15 B.13或14 C.13或14或15 D.14或15或16
二.填空题
9.三角形具有稳定性,要使一个四边形框架稳定不变形,至少需要钉 根木条.
10.如图,则x的值为 .
11.如果一个多边形的每个外角都是60°,那么这个多边形内角和的度数为 .
12.一个凸n边形的内角和是540°,则n= .
13.如图,五边形ABCDE中,AB∥DE,BC⊥CD,∠1、∠2分别是与∠ABC、∠CDE相邻的外角,则∠1+∠2等于 度.
14.如图,小亮从A点出发前进2m,向右转15°,再前进2m,又向右转15°,…,这样一直走下去,他第一次回到出发点A时,一共走了 m.
15.为庆祝中国共产党建党100周年,某校用红色灯带制作了一个如图所示的正五角星(A,B,C,D,E是正五角星的五个顶点),则图中∠A的度数是 度.
16.如图,∠A+∠B+∠C+∠D+∠E= °.
三.解答题
17.求出下列图形中x的值.
18.已知,四边形ABCD中,∠C+∠D=200°,∠B=3∠A,求∠A和∠B的度数.
19.在一个各内角都相等的多边形中,每一个内角都比与它相邻外角的3倍还大20°,求这个多边形的边数以及它的内角和.
20.如图,五角星的顶点为A、B、C、D、E,求∠A+∠B+∠C+∠D+∠E的度数?
21.观察每个正多边形中∠α的变化情况,解答下列问题:
(1)将下面的表格补充完整:
正多边形边数 3 4 5 6 … 18
∠α的度数 …
(2)根据规律,是否存在一个正n边形,使其中的∠α=21°?若存在,直接写出n的值;若不存在,请说明理由.
22.如图①,在四边形ABCD中,∠A=x°,∠C=y°.
(1)∠ABC+∠ADC= °(用含x,y的代数式表示);
(2)BE、DF分别为∠ABC、∠ADC的外角平分线,
①当x=y时,BE与DF的位置关系是 ;
②当y=2x时,若BE与DF交于点P,且∠DPB=10°,求y的值.
(3)如图②,∠ABC的平分线与∠ADC的外角平分线交于点Q,则∠Q= (用含x,y的代数式表示).
参考答案
一.选择题
1.解:A.三角形的内角和为180°;
B.四边形的内角和为360°;
C.五边形的内角和为:(5﹣2)×180°=540°;
D.六边形的内角和为:(6﹣2)×180°=720°;
故选:D.
2.解:过五边形的一个顶点作对角线,有5﹣3=2条对角线,所以至少要钉上2根木条.
故选:B.
3.解:∵正多边形的外角和为360°,
∴此多边形的边长为:360°÷60°=6.
故选:B.
4.解:∵∠1+∠DAB=180°,∠3+∠BCD=180°,
∴∠1+∠3+∠DAB+∠BCD=360°,
∵∠ABC+∠BCD+∠D+∠DAB=360°,
∴∠1+∠3=∠ABC+∠D,
故A符合题意;
∵∠1+∠3只有∠ABC和∠D互补时才等于180°,
故B不符合题意;
∵只有∠ABC和∠D互补时,∠2=∠D,
故C不符合题意;
∵多边形的外角和是360°,
∴∠1+∠2+∠3<360°,
故D不符合题意;
故选:A.
5.解:根据正多边形内角和公式可得,
正五边形ABCDE的内角和=180°×(5﹣2)=540°,
则∠BAE=∠B=∠E==108°,
根据正五边形的性质,△ABC≌△AED,
∴∠CAB=∠DAE=(180°﹣108°)=36°,
∴∠CAD=108°﹣36°﹣36°=36°,
故选:C.
6.解:根据题意可知,他需要转360÷45=8次才会回到原点,
所以一共走了8×6=48(米).
故选:C.
7.解:设这个正多边形的边数为n,
由题意得:(n﹣2)×180=360,
解得:n=9,
故选:C.
8.解:如图,n边形,A1A2A3…An,
若沿着直线A1A3截去一个角,所得到的多边形,比原来的多边形的边数少1,
若沿着直线A1M截去一个角,所得到的多边形,与原来的多边形的边数相等,
若沿着直线MN截去一个角,所得到的多边形,比原来的多边形的边数多1,
因此将一个多边形截去一个角后,变成十四边形,则原来的多边形的边数为13或14或15,
故选:C.
二.填空题
9.解:如图所示:
要使这个木架不变形,他至少还要再钉上1个木条,
故答案为:1
10.解:因为四边形的内角和是360°,
根据题意得,x+x+90+120=360,
解得,x=75,
故答案为:75.
11.解:∵一个多边形的每个外角都是60°,
∴n=360°÷60°=6,
则内角和为:(6﹣2)?180°=720°,
故答案为:720°.
12.解:根据题意得,
(n﹣2)?180°=540°,
解得n=5,
故答案为:5.
13.解:连接BD,
∵BC⊥CD,
∴∠C=90°,
∴∠CBD+∠CDB=180°﹣90°=90°,
∵AB∥DE,
∴∠ABD+∠EDB=180°,
∴∠1+∠2=(180°﹣∠ABC)+(180°﹣∠EDC)
=360°﹣(∠ABC+∠EDC)
=360°﹣(∠ABD+∠CBD+∠EDB+∠CDB)
=360°﹣(90°+180°)
=90°,
故答案为:90.
14.解:∵小亮从A点出发最后回到出发点A时正好走了一个正多边形,
∴根据外角和定理可知正多边形的边数为:360°÷15°=24,
则一共走了:24×2=48(m),
故答案为:48.
15.解:如图,
∵正五角星中,五边形FGHMN是正五边形,
∴∠GFN=∠FNM==108°,
∴∠AFN=∠ANF=180°﹣∠GFN=180°﹣108°=72°,
∴∠A=180°﹣∠AFN﹣∠ANF=180°﹣72°﹣72°=36°.
故答案是:36.
16.解:如图,设线段BD,BE分别与线段AC交于点N,M.
∵∠AMB=∠A+∠E,∠DNC=∠B+∠AMB,∠DNC+∠D+∠C=180°,
∴∠A+∠B+∠D+∠E+∠C=180°,
故答案为:180.
三.解答题
17.解:(1)由三角形的外角性质得,x+(x+10)=x+70,
即2x+10=x+70,
解得,x=60.
(2)根据四边形的内角和为360°得,
x+(x+10)+90+60=360,
解得,x=100.
18.解:∵四边形内角和360°,∠C+∠D=200°,
∴∠B+∠A=360°﹣200°=160°,
∵∠B=3∠A,
∴3∠A+∠A=160°,
∴∠A=40°,
∴∠B=120°.
答:∠A和∠B的度数分别是40°和120°.
19.解:设多边形的一个外角为α,则与其相邻的内角等于3α+20°,
由题意,得(3α+20°)+α=180°,解得α=40°,
即多边形的每个外角为40°,
又∵多边形的外角和为360°,
∴多边形的外角个数==9,
∴多边形的边数=9,
∴多边形的内角和=(9﹣2)×180°=1260°.
20.解:如图,
由三角形的外角性质得,∠AGE=∠A+∠C,∠DFE=∠B+∠D,
∵∠AGE+∠DFE+∠E=180°,
∴∠A+∠B+∠C+∠D+∠E=180°.
21.解:(1)填表如下:
正多边形的边数 3 4 5 6 …… 18
∠α的度数 60° 45° 36° 30° …… 10°
故答案为:60°,45°,36°,30°,10°;
(2)不存在,理由如下:
假设存在n边形使得∠α=21°,得∠α=21°=()°,
解得:n=8,又n是正整数,
所以不存在正n边形使得∠α=21°.
22.解:(1)在四边形ABCD中,∠ABC+∠ADC=360°﹣∠A﹣∠DCB,
∵∠A=x°,∠DCB=y°,
∴∠ABC+∠ADC=360﹣x﹣y=(360﹣x﹣y)°,
故答案为:(360﹣x﹣y),
(2)①如图①中,
连接AC,过点C作CG∥DF,则有:
∠MDC═∠DAC+∠DCA,∠NBC═∠CAB+∠CBA,
∵BE、DF分别为∠NBC、∠MDC的角平分线,∠DAB═∠DCB═x°═y°,
∴∠FDC+∠CBE═(∠MDC+∠NBC)═(∠DAC+∠DCA+∠CAB+∠CBA)═(∠DAB+DCB)═x°,
∵CG∥DF,
∴∠FDC═∠GCD,
∵∠DCG+∠BCG═∠DCB═x°,∠FDC+∠CBE═x°,
∴∠CBE═∠BCG,
∴CG∥BE,
∴BE∥DF,
故答案为:BE∥DF.
②由(1)可知:∠ABC+∠ADC=(360﹣x﹣y)°,
∵∠ADC+∠MDC=180°,∠ABC+∠NBC=180°,
∴∠NBC+∠MDC=(x+y)°,
∵BE、DF分别为∠ABC、∠ADC的外角平分线,
∴∠PBC=∠NBC,∠PDC=∠MDC,
∴∠PBC+∠PDC=[(x+y)]°,
∵∠BCD=∠PDC+∠PBC+∠P,
∴y=10+(x+y),
即y﹣x=20,
∵y=2x,
∴x=20°,y=40°.
(3)如图②中,
由题意:∠DNQ=∠ANB=180°﹣x°﹣∠ABC,∠QDN=(180°﹣∠ADC),
∴∠Q=180°﹣∠DNQ﹣∠QDN=180°﹣(180°﹣x°﹣∠ABC)﹣(180°﹣∠ADC),
=x°+(∠ABC+∠ADC)﹣90°,
=x°+180°﹣(x+y)°﹣90°,
=[90+(x﹣y)]°,
故答案为:[90+(x﹣y)]°.
