2021年暑假自主学习《1.1探索勾股定理》基础达标训练(附答案) 北师大版八年级数学上册
文档属性
| 名称 | 2021年暑假自主学习《1.1探索勾股定理》基础达标训练(附答案) 北师大版八年级数学上册 |  | |
| 格式 | doc | ||
| 文件大小 | 625.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 10:53:03 | ||
图片预览



文档简介
2021年北师大版八年级数学上册《1.1探索勾股定理》暑假自主学习基础达标训练(附答案)
1.在直角三角形中,若两直角边分别为3和4,则斜边为( )
A.5 B.6 C.7 D.8
2.在Rt△中,,,则( )
A.9 B.18 C.20 D.24
3.折叠长方形的一边,使点落在边的点处,若,求的长为( )
A. B. C. D.
4.若直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是( )
A.60 B.30 C.20 D.32
5.下列各组数中,属于勾股数的是( )
A.2.5,6,6.5 B.5,7,10 C.,,, D.6,8,10
6.如图,以直角三角形的一条直角边和斜边为一边作正方形M和N,它们的面积分别为9平方厘米和25平方厘米,则直角三角形的面积为( )
A.6平方厘米 B.12平方厘米 C.24平方厘米 D.3平方厘米
7.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24 cm.则蚂蚁爬行的最短距离为_______.
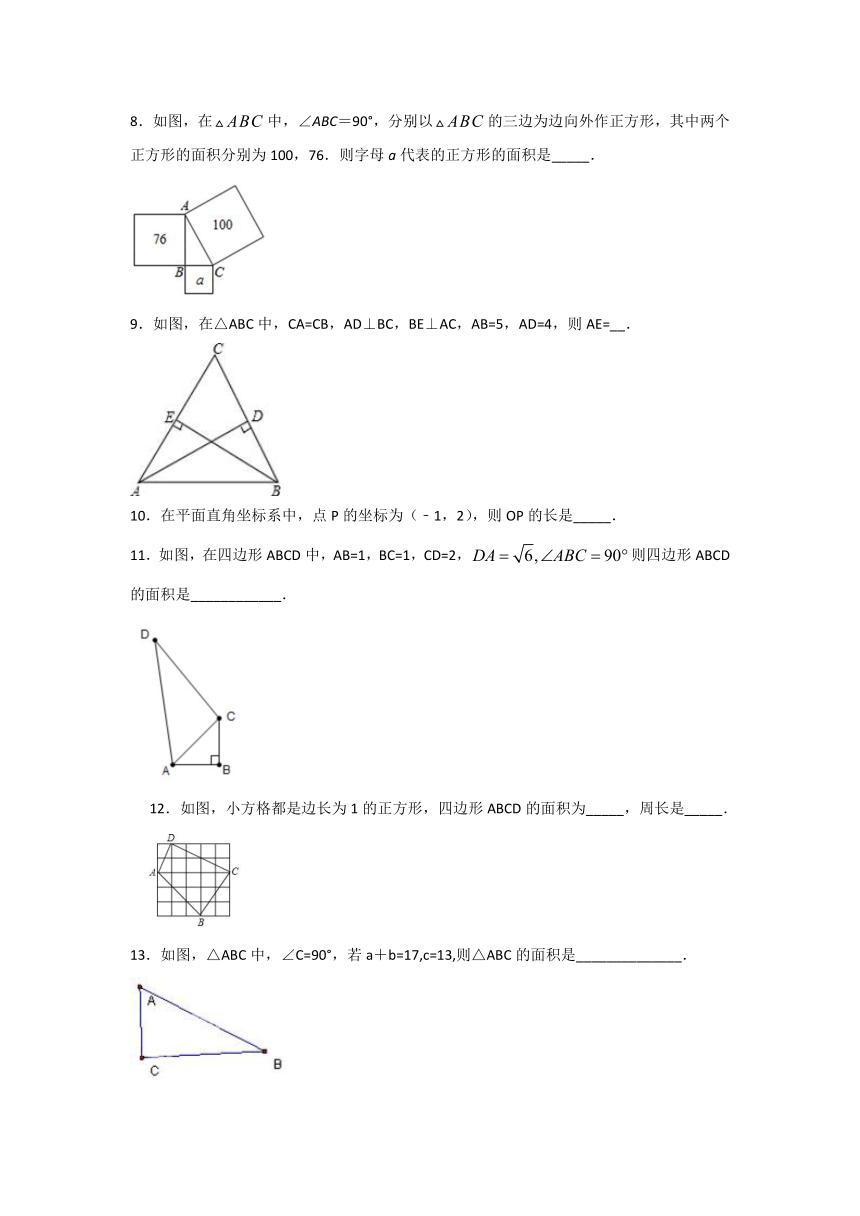
8.如图,在中,∠ABC=90°,分别以的三边为边向外作正方形,其中两个正方形的面积分别为100,76.则字母a代表的正方形的面积是_____.
9.如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE=__.
10.在平面直角坐标系中,点P的坐标为(﹣1,2),则OP的长是_____.
11.如图,在四边形ABCD中,AB=1,BC=1,CD=2,则四边形ABCD的面积是____________.
12.如图,小方格都是边长为1的正方形,四边形ABCD的面积为_____,周长是_____.
13.如图,△ABC中,∠C=90°,若a+b=17,c=13,则△ABC的面积是______________.
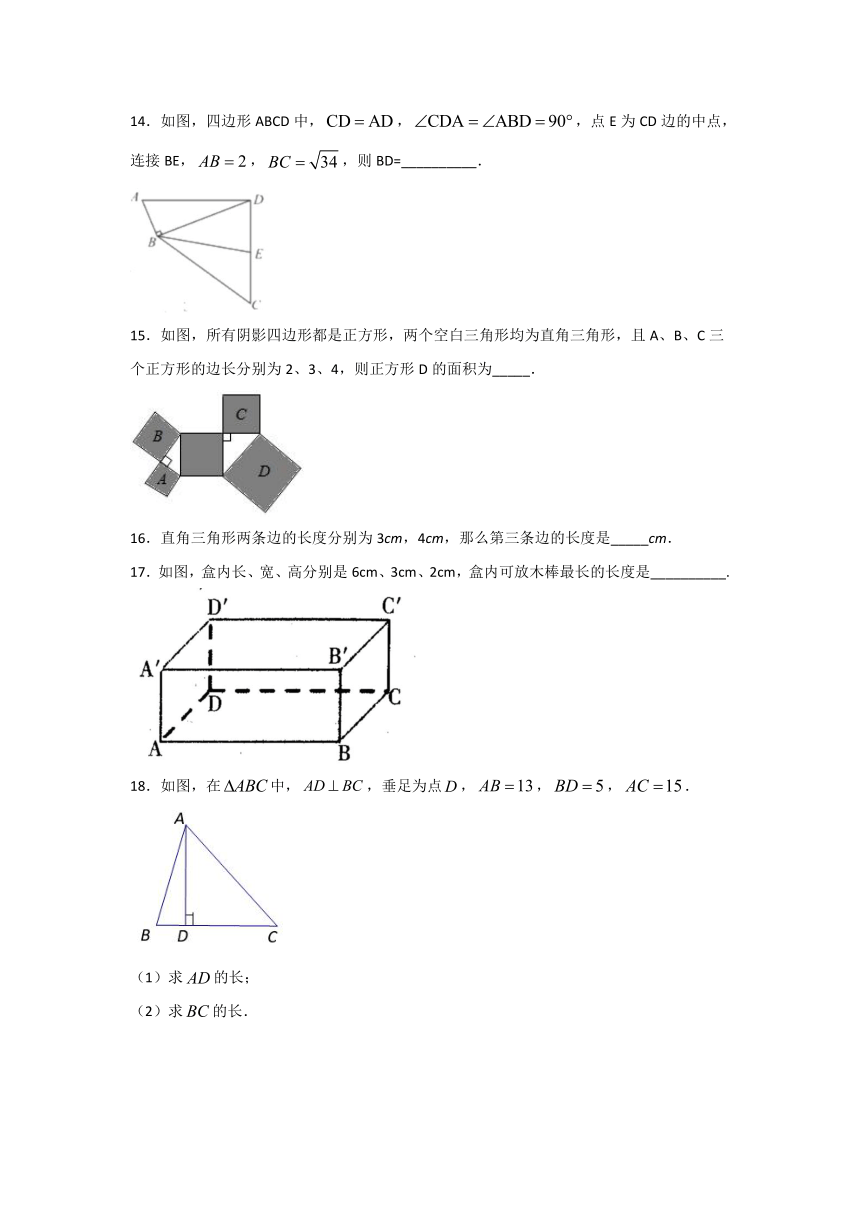
14.如图,四边形ABCD中,,,点E为CD边的中点,连接BE,,,则BD=__________.
15.如图,所有阴影四边形都是正方形,两个空白三角形均为直角三角形,且A、B、C三个正方形的边长分别为2、3、4,则正方形D的面积为_____.
16.直角三角形两条边的长度分别为3cm,4cm,那么第三条边的长度是_____cm.
17.如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是__________.
18.如图,在中,,垂足为点,,,.
(1)求的长;
(2)求的长.
19.如图所示,有一个直角三角形纸片,两直角边,,现将直角边沿直线折叠,使它落在斜边上且与重合,你能求出的长吗?
20.如图,在四边形中,,,,且,求的度数.
21.如图所示,已知在中,,折叠使,两点重合,折痕交于点,交于点,,于点,求的长.
22.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为D,CD=8.求AC的长.
23.如图在中,,点E,F分别在上,求证:.
参考答案
1 2 3 4 5 6
A B A B D A
7.
解:如图,将圆柱形容器侧面展开,连接AB,则AB即为最短距离.
在Rt△ABC中,∠ACB=90°,
AC = cm,
BC= 12-3-3= 6cm,
(cm),
即蚂蚁从外壁A到达外壁B处的最短距离为cm.
故答案为:6cm.
8.24
解:∵两个正方形的面积分别为100,76,
∴AB2=76,AC2=100,
∵在△ABC中,∠ABC=90°,
∴BC2+AB2=AC2,
∴BC2=.
故字母a代表的正方形的面积是24
故答案为24.
9.3
解:∵在△ABC中,CA=CB,AD⊥BC,BE⊥AC,∴△ABD≌△BAE(AAS).∴AD=BE=4.
∵AB=5,∴.
10.
解:OP的长=,故答案为:.
11.
解:在中,,,
在中,,,,则,
∴是直角三角形,
.
故答案是:.
12.12.5, 3++3.
解:四边形ABCD的面积为:5×5﹣×1×2﹣×2×4﹣×3×3﹣×2×3=12.5;
AD==,
AB==3,
BC==;
DC==2,
故四边形ABCD的周长是: +3++2=3++3.
故答案为:12.5;3++3.
13.30
解:如图,
∵△ABC中,∠C=90°,
∴a2+b2=c2,
∴(a+b)2﹣2ab=c2,
又∵a+b=17,c=13,
∴ab=60.
∴△ABC的面积是ab=30.
故答案是:30.
14.5
解:如图,过点C作CF⊥BD于点F,
∴∠CFD=90°,
∵,
∴∠A+∠ADB=90°,∠ADB+∠CDF=90°,
∴∠A=∠CDF,
又∵,
在△ ABD和△DFC中,
,
∴△ABD≌△DFC,
∴CF=BD,AB=DF=2,
∴,
∴,
解得:,
∴,故答案为:5.
15.9
解:设正方形A,B,C,D的边长分别为a,b,c,d,根据勾股定理得
,
∵正方形A、B、C的面积依次为2、4、3,
∴根据图形得:2+4=﹣3,
解得:=9,
故答案为:9.
16.5或
解:当这个直角三角形的两直角边分别为、时,
则该三角形的斜边的长为:(),
当这个直角三角形的一条直角边为,斜边为时,
则该三角形的另一条直角边的长为:().
故答案为或.
17.7cm
解:本题需先求出长和宽组成的长方形的对角线长为cm.
这根最长的棍子和矩形的高,以及长和宽组成的长方形的对角线组成了直角三角形.
盒内可放木棒最长的长度是 =7cm.
故答案为:7.
18.(1);(2).
解:(1),
,
在中,,
,
,
,
.
(2)在中,,
,
,
,
.
.
19.3
解:在三角形ABC中,由勾股定理可知:
.
由折叠的性质可知:
,,.
∴,.
设,则.
在中,由勾股定理得:
,即.
解得:.
∴.
20..
解:如图,连接,
在中,.
因为,
所以,
在中,,
所以为直角三角形,,
所以.
21..
解:由折叠的性质可知:, .
又∵,
∴.
∵,
∴△ADE为等腰直角三角形,AE=DE
由勾股定理,得,
∴,
∴.
22.AC=
解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
在Rt△BCD中,BD==6,
设AC=AB=x,则AD=x﹣6,
在Rt△ACD中,AC2=AD2+CD2,即x2=(x﹣6)2+82,
解得,x=,即AC=.
23.解:
,均为直角三角形
在中,
在中,
在中,
在中,
1.在直角三角形中,若两直角边分别为3和4,则斜边为( )
A.5 B.6 C.7 D.8
2.在Rt△中,,,则( )
A.9 B.18 C.20 D.24
3.折叠长方形的一边,使点落在边的点处,若,求的长为( )
A. B. C. D.
4.若直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是( )
A.60 B.30 C.20 D.32
5.下列各组数中,属于勾股数的是( )
A.2.5,6,6.5 B.5,7,10 C.,,, D.6,8,10
6.如图,以直角三角形的一条直角边和斜边为一边作正方形M和N,它们的面积分别为9平方厘米和25平方厘米,则直角三角形的面积为( )
A.6平方厘米 B.12平方厘米 C.24平方厘米 D.3平方厘米
7.如图,圆柱形容器外壁距离下底面3cm的A处有一只蚂蚁,它想吃到正对面外壁距离上底面3cm的B处的米粒,若圆柱的高为12cm,底面周长为24 cm.则蚂蚁爬行的最短距离为_______.
8.如图,在中,∠ABC=90°,分别以的三边为边向外作正方形,其中两个正方形的面积分别为100,76.则字母a代表的正方形的面积是_____.
9.如图,在△ABC中,CA=CB,AD⊥BC,BE⊥AC,AB=5,AD=4,则AE=__.
10.在平面直角坐标系中,点P的坐标为(﹣1,2),则OP的长是_____.
11.如图,在四边形ABCD中,AB=1,BC=1,CD=2,则四边形ABCD的面积是____________.
12.如图,小方格都是边长为1的正方形,四边形ABCD的面积为_____,周长是_____.
13.如图,△ABC中,∠C=90°,若a+b=17,c=13,则△ABC的面积是______________.
14.如图,四边形ABCD中,,,点E为CD边的中点,连接BE,,,则BD=__________.
15.如图,所有阴影四边形都是正方形,两个空白三角形均为直角三角形,且A、B、C三个正方形的边长分别为2、3、4,则正方形D的面积为_____.
16.直角三角形两条边的长度分别为3cm,4cm,那么第三条边的长度是_____cm.
17.如图,盒内长、宽、高分别是6cm、3cm、2cm,盒内可放木棒最长的长度是__________.
18.如图,在中,,垂足为点,,,.
(1)求的长;
(2)求的长.
19.如图所示,有一个直角三角形纸片,两直角边,,现将直角边沿直线折叠,使它落在斜边上且与重合,你能求出的长吗?
20.如图,在四边形中,,,,且,求的度数.
21.如图所示,已知在中,,折叠使,两点重合,折痕交于点,交于点,,于点,求的长.
22.如图,在△ABC中,AB=AC,BC=10,CD⊥AB,垂足为D,CD=8.求AC的长.
23.如图在中,,点E,F分别在上,求证:.
参考答案
1 2 3 4 5 6
A B A B D A
7.
解:如图,将圆柱形容器侧面展开,连接AB,则AB即为最短距离.
在Rt△ABC中,∠ACB=90°,
AC = cm,
BC= 12-3-3= 6cm,
(cm),
即蚂蚁从外壁A到达外壁B处的最短距离为cm.
故答案为:6cm.
8.24
解:∵两个正方形的面积分别为100,76,
∴AB2=76,AC2=100,
∵在△ABC中,∠ABC=90°,
∴BC2+AB2=AC2,
∴BC2=.
故字母a代表的正方形的面积是24
故答案为24.
9.3
解:∵在△ABC中,CA=CB,AD⊥BC,BE⊥AC,∴△ABD≌△BAE(AAS).∴AD=BE=4.
∵AB=5,∴.
10.
解:OP的长=,故答案为:.
11.
解:在中,,,
在中,,,,则,
∴是直角三角形,
.
故答案是:.
12.12.5, 3++3.
解:四边形ABCD的面积为:5×5﹣×1×2﹣×2×4﹣×3×3﹣×2×3=12.5;
AD==,
AB==3,
BC==;
DC==2,
故四边形ABCD的周长是: +3++2=3++3.
故答案为:12.5;3++3.
13.30
解:如图,
∵△ABC中,∠C=90°,
∴a2+b2=c2,
∴(a+b)2﹣2ab=c2,
又∵a+b=17,c=13,
∴ab=60.
∴△ABC的面积是ab=30.
故答案是:30.
14.5
解:如图,过点C作CF⊥BD于点F,
∴∠CFD=90°,
∵,
∴∠A+∠ADB=90°,∠ADB+∠CDF=90°,
∴∠A=∠CDF,
又∵,
在△ ABD和△DFC中,
,
∴△ABD≌△DFC,
∴CF=BD,AB=DF=2,
∴,
∴,
解得:,
∴,故答案为:5.
15.9
解:设正方形A,B,C,D的边长分别为a,b,c,d,根据勾股定理得
,
∵正方形A、B、C的面积依次为2、4、3,
∴根据图形得:2+4=﹣3,
解得:=9,
故答案为:9.
16.5或
解:当这个直角三角形的两直角边分别为、时,
则该三角形的斜边的长为:(),
当这个直角三角形的一条直角边为,斜边为时,
则该三角形的另一条直角边的长为:().
故答案为或.
17.7cm
解:本题需先求出长和宽组成的长方形的对角线长为cm.
这根最长的棍子和矩形的高,以及长和宽组成的长方形的对角线组成了直角三角形.
盒内可放木棒最长的长度是 =7cm.
故答案为:7.
18.(1);(2).
解:(1),
,
在中,,
,
,
,
.
(2)在中,,
,
,
,
.
.
19.3
解:在三角形ABC中,由勾股定理可知:
.
由折叠的性质可知:
,,.
∴,.
设,则.
在中,由勾股定理得:
,即.
解得:.
∴.
20..
解:如图,连接,
在中,.
因为,
所以,
在中,,
所以为直角三角形,,
所以.
21..
解:由折叠的性质可知:, .
又∵,
∴.
∵,
∴△ADE为等腰直角三角形,AE=DE
由勾股定理,得,
∴,
∴.
22.AC=
解:∵CD⊥AB,
∴∠ADC=∠BDC=90°,
在Rt△BCD中,BD==6,
设AC=AB=x,则AD=x﹣6,
在Rt△ACD中,AC2=AD2+CD2,即x2=(x﹣6)2+82,
解得,x=,即AC=.
23.解:
,均为直角三角形
在中,
在中,
在中,
在中,
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
