2021年暑假自主学习《1.3正方形的性质与判定》能力提升训练(附答案) 北师大版九年级数学上册
文档属性
| 名称 | 2021年暑假自主学习《1.3正方形的性质与判定》能力提升训练(附答案) 北师大版九年级数学上册 |  | |
| 格式 | doc | ||
| 文件大小 | 290.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 10:53:50 | ||
图片预览

文档简介
2021年北师大版九年级数学上册《1.3正方形的性质与判定》暑假自主学习
能力提升训练(附答案)
1.已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
2.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED为( )
A.15° B.35° C.45° D.55°
3.如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为( )
A.15° B.22.5° C.25° D.17.5°
4.如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到如图所示的位置,使得点B落在对角线CF上,则阴影部分的面积是 .
5.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
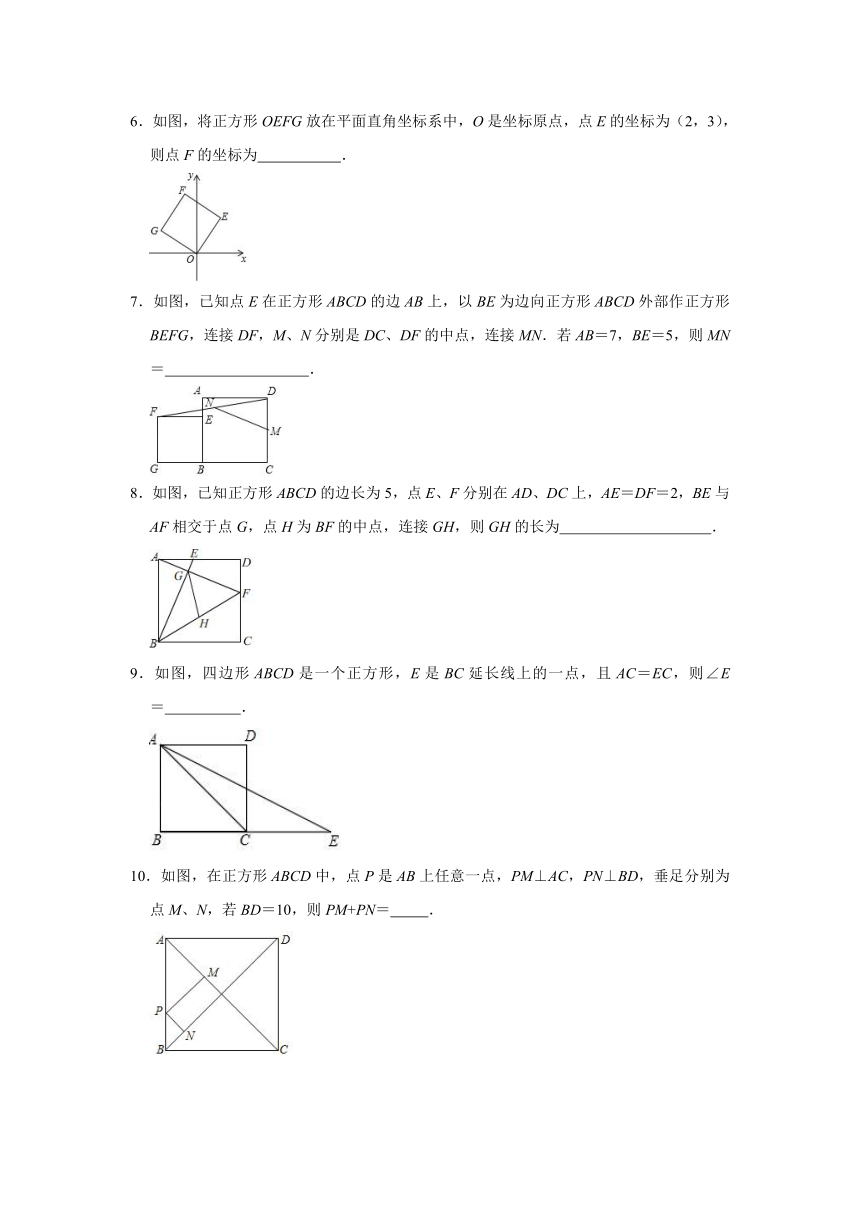
6.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .
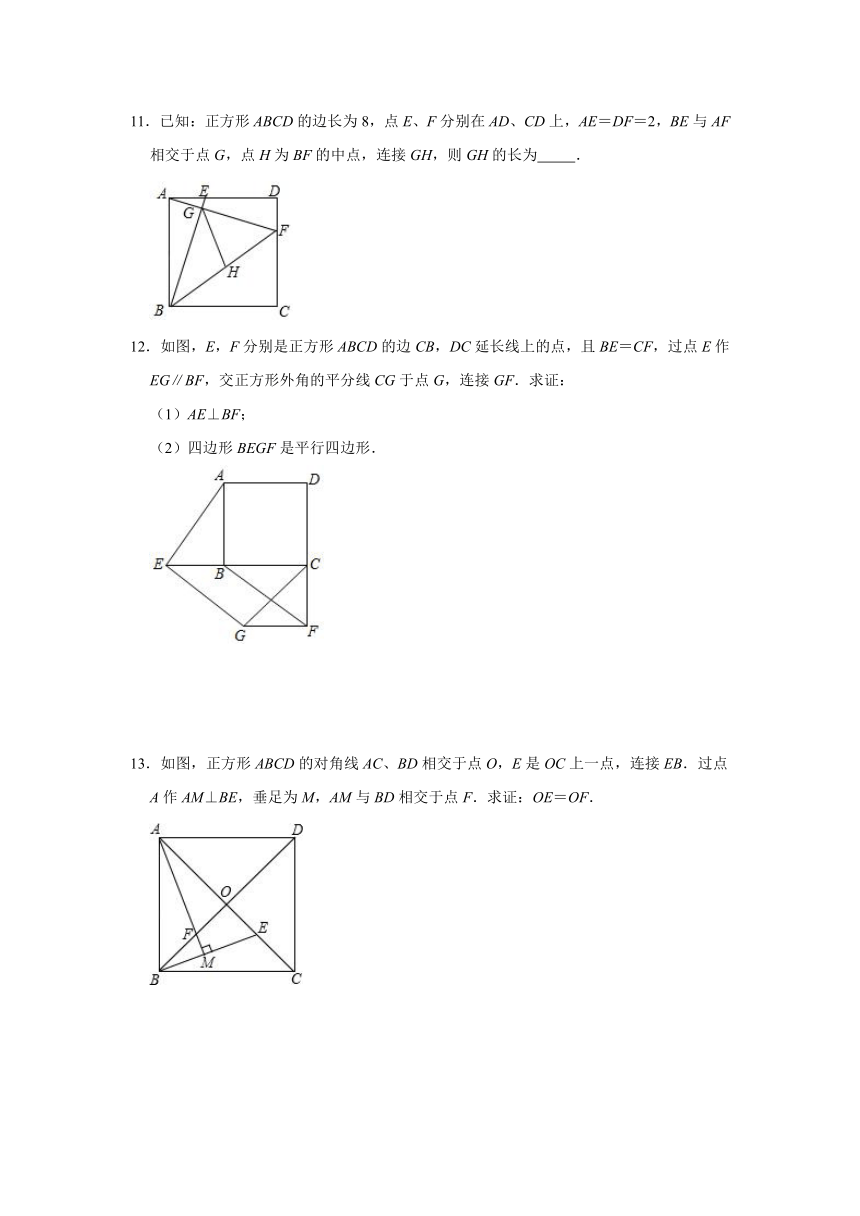
7.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN= .
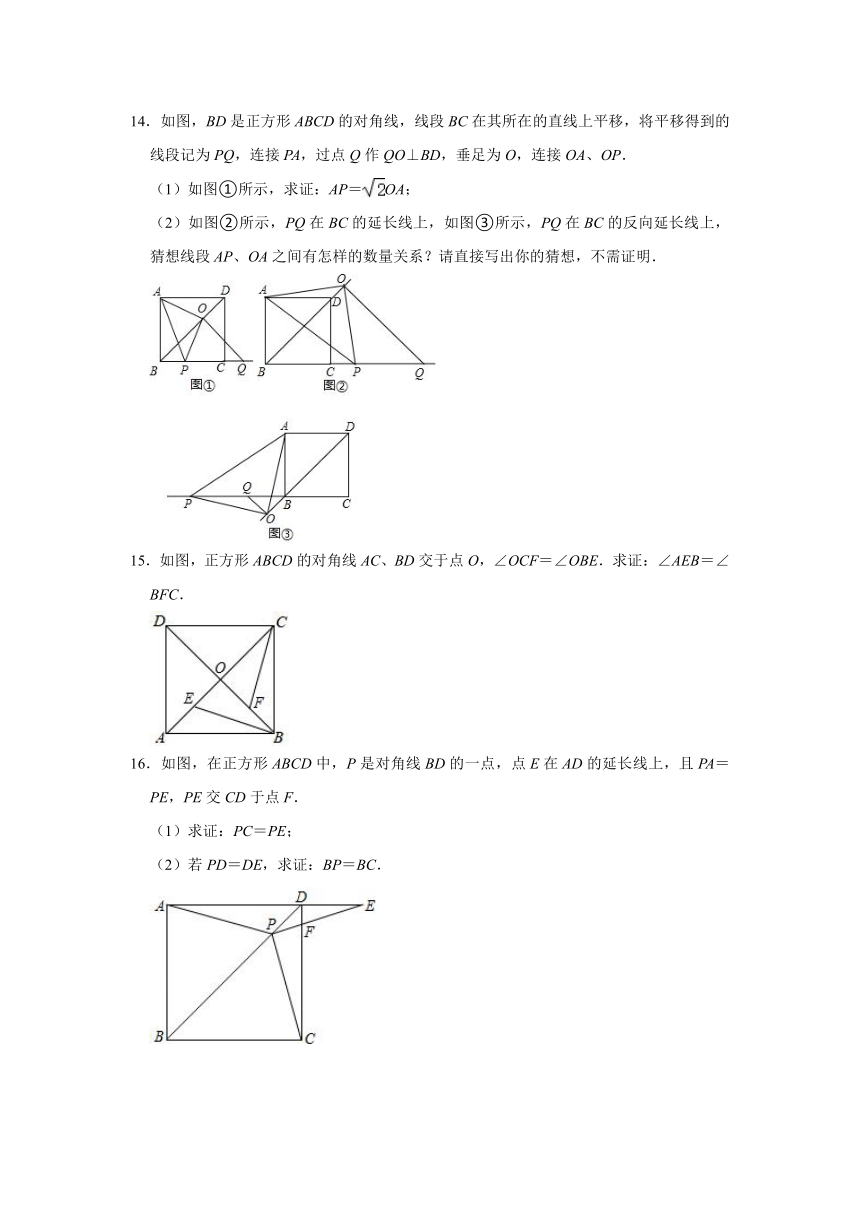
8.如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
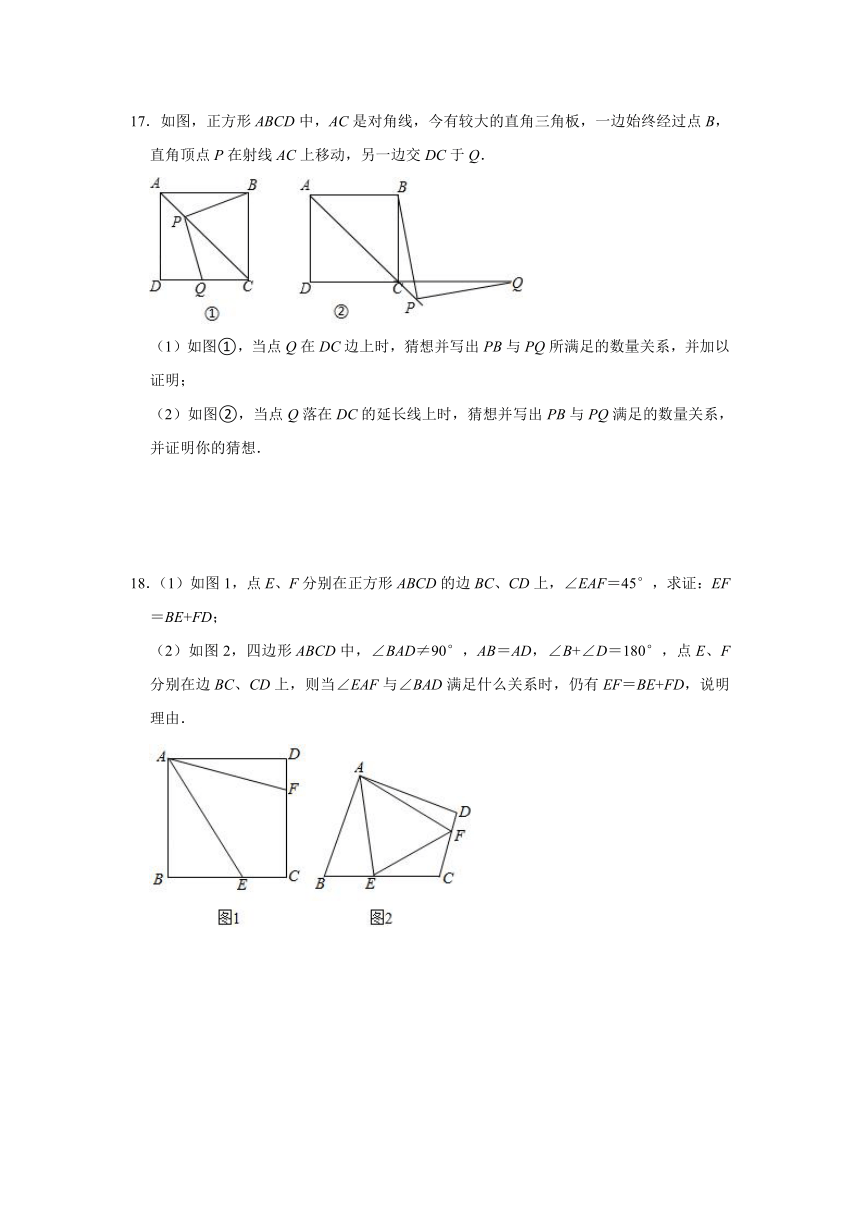
9.如图,四边形ABCD是一个正方形,E是BC延长线上的一点,且AC=EC,则∠E= .
10.如图,在正方形ABCD中,点P是AB上任意一点,PM⊥AC,PN⊥BD,垂足分别为点M、N,若BD=10,则PM+PN= .
11.已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
12.如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
13.如图,正方形ABCD的对角线AC、BD相交于点O,E是OC上一点,连接EB.过点A作AM⊥BE,垂足为M,AM与BD相交于点F.求证:OE=OF.
14.如图,BD是正方形ABCD的对角线,线段BC在其所在的直线上平移,将平移得到的线段记为PQ,连接PA,过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)如图①所示,求证:AP=OA;
(2)如图②所示,PQ在BC的延长线上,如图③所示,PQ在BC的反向延长线上,猜想线段AP、OA之间有怎样的数量关系?请直接写出你的猜想,不需证明.
15.如图,正方形ABCD的对角线AC、BD交于点O,∠OCF=∠OBE.求证:∠AEB=∠BFC.
16.如图,在正方形ABCD中,P是对角线BD的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)若PD=DE,求证:BP=BC.
17.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
18.(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
19.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
20.如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以每秒3cm的速度向点B移动,点Q以每秒2cm测得速度向点D移动,当点P到达点B处时,两点均停止移动
(1)P,Q两点出发多长时间,线段PQ的长度为10cm?
(2)是否存在某一时刻,使四边形PBCQ为正方形?若存在,求出该时刻;若不存在,请说明理由.
参考答案
1.解:A、根据平行四边形的性质得到OA=OC,OB=OD,该结论正确;
B、当AB=CD时,四边形ABCD还是平行四边形,该选项错误;
C、根据有一个角是直角的平行四边形是矩形可以判断该选项正确;
D、当AC=BD且AC⊥BD时,根据对角线相等可判断四边形ABCD是矩形,根据对角线互相垂直可判断四边形ABCD 是菱形,故四边形ABCD是正方形,该结论正确;
故选:B.
2.解:在正方形ABCD中,AB=AD,∠BAD=90°,
在等边△ABE中,AB=AE,∠BAE=∠AEB=60°,
在△ADE中,AD=AE,∠DAE=∠BAD+∠BAE=90°+60°=150°,
所以,∠AED=(180°﹣150°)=15°,
所以∠BED=∠AEB﹣∠AED=60°﹣15°=45°.
故选:C.
3.解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣67.5°=22.5°.
故选:B.
4.解:方法一:正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,
∴EF=CE=1,
∴CF=,
∴BF=﹣1,
∵∠BFE=45°,
∴阴影部分的面积=×1×1﹣×(﹣1)2=﹣1;
方法二:∵过E点作MN∥BC交AB、CD于M、N点,设AB与EF交于点P点,连接CP,如下图所示,
∵B在对角线CF上,
∴∠DCE=∠ECF=45°,EC=1,
∴△ENC为等腰直角三角形,
∴MB=CN=EC=,
又BC=AD=CD=CE,且CP=CP,△PEC和△PBC均为直角三角形,
∴Rt△PEC≌Rt△PBC(HL),
∴PB=PE,
又∠PFB=45°,
∴∠FPB=45°=∠MPE,
∴△MPE为等腰直角三角形,
设MP=x,则EP=BP=,
∵MP+BP=MB,
∴,解得,
∴BP=,
∴阴影部分的面积=.
故答案为:.
5.解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA﹣AE=OC﹣CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF==2,
由勾股定理得:DE===2,
∴四边形BEDF的周长=4DE=4×=8,
故答案为:8.
6.解:如图,过点E作x轴的垂线EH,垂足为H.过点G作x轴的垂线GM,垂足为M,连接GE、FO交于点O′.
∵四边形OEFG是正方形,
∴OG=EO,∠GOM=∠OEH,∠OGM=∠EOH,
在△OGM与△EOH中,
∴△OGM≌△EOH(ASA)
∴GM=OH=2,OM=EH=3,
∴G(﹣3,2).
∴O′(﹣,).
∵点F与点O关于点O′对称,
∴点F的坐标为 (﹣1,5).
故答案是:(﹣1,5).
7.解:连接CF,
∵正方形ABCD和正方形BEFG中,AB=7,BE=5,
∴GF=GB=5,BC=7,
∴GC=GB+BC=5+7=12,
∴=13.
∵M、N分别是DC、DF的中点,
∴MN==.
故答案为:.
8.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=5、CF=CD﹣DF=5﹣2=3,
∴BF==,
∴GH=BF=,
故答案为:.
9.解:∵四边形ABCD是正方形,
∴∠ACB=45°,AD∥BC,
∵AC=EC,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE=2∠E,
∴∠E=∠ACB=22.5°,
故答案为:22.5°.
10.解:在正方形ABCD中,
∴AC⊥BD,∠ABO=45°,
∵PM⊥AC,PN⊥BD,
∴四边形PMON是矩形,
∴PM=ON,
∵PN=BN,
∴PM+PN=ON+BN=OB=BD=5,
故答案为:5
11.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
∵AB=AD,∠BAE=∠D,AE=DF
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=8,CF=CD﹣DF=8﹣2=6
∴BF==10
∴GH=5
故答案为:5
12.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
13.证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
∴△BOE≌△AOF(AAS).
∴OE=OF.
14.(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,
∴∠BOQ=90°,
∴∠BQO=∠CBD=45°,
∴OB=OQ,
∵PQ=BC,
∴AB=PQ,
在△ABO和△PQO中,,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,
∴∠BOP+∠AOB=90,即∠AOP=90°,
∴△AOP是等腰直角三角形,
∴AP=OA;
(2)解:PQ在BC的延长线上,线段AP、OA之间的数量关系为:AP=OA;理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,
∴∠BOQ=90°,
∴∠BQO=∠CBD=45°,
∴OB=OQ,
∵PQ=BC,
∴AB=PQ,
在△ABO和△PQO中,,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,
∴∠BOP+∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,
∴AP=OA;
PQ在BC的反向延长线上,线段AP、OA之间的数量关系为:AP=OA;理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,
∴∠BOQ=90°,
∴∠BQO=∠CBD=∠OBQ=45°,
∴OB=OQ,∠ABO=∠PQO=135°,
∵PQ=BC,
∴AB=PQ,
在△ABO和△PQO中,,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP﹣∠POQ=90°,
∴∠BOP﹣∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,
∴AP=OA.
15.证明:∵四边形ABCD是正方形,
∴AC⊥BD,即∠AOB=∠BOC=90°,
∴OB=OC,
在△OCF和△OBE中,
,
∴△OCF≌△OBE(ASA),
∴∠OFC=∠OEB,
∴∠BFC=∠AEB.
16.(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP,
在△ADP和△CDP中,
,
∴△ADP≌△CDP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE.
(2)证明:四边形ABCD为正方形,
∴∠ADC=∠CDE=90°,
∴∠E+∠DFE=90°,
∵PA=PE,
∴∠PAD=∠E,
由(1)知△ADP≌△CDP,
∴∠PAD=∠PCD,
∴∠PCD=∠E,
∵∠PFC=∠DFE,
∴∠PCD+∠PFC=∠E+∠DFE=90°,
∴∠CPE=90°,
∴∠BPC+∠DPE=90°,
∵PD=DE,
∴∠DPE=∠E,
∴∠DPE=∠PCD,
∵∠BCP+∠PCD=90°,
∴∠BPC=∠BCP,
∴BP=BC.
17.解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
18.证明:(1)如图1:把△ABE绕点A逆时针旋转90°至△ADG,
则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BEA=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△EAF中,
,
∴△GAF≌△EAF(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF;
(2)当∠BAD=2∠EAF时,仍有EF=BE+FD,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
19.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
20.解:(1)过点P作PH⊥CD于点H,
∴HQ=16﹣5t,
∴PQ2=PH2+HQ2,
即102=(16﹣5t)2+62,
解得:,
答:P,Q两点出发或秒,线段PQ的长度为10cm;
(2)假设四边形PBCQ是正方形,
∴BP=CQ,即16﹣3t=2t,
解得:t=,
∵,
∴不成立.
能力提升训练(附答案)
1.已知四边形ABCD是平行四边形,AC,BD相交于点O,下列结论错误的是( )
A.OA=OC,OB=OD
B.当AB=CD时,四边形ABCD是菱形
C.当∠ABC=90°时,四边形ABCD是矩形
D.当AC=BD且AC⊥BD时,四边形ABCD是正方形
2.如图,在正方形ABCD的外侧,作等边△ABE,则∠BED为( )
A.15° B.35° C.45° D.55°
3.如图,正方形ABCD的对角线AC,BD交于点O,P为边BC上一点,且BP=OB,则∠COP的度数为( )
A.15° B.22.5° C.25° D.17.5°
4.如图,正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到如图所示的位置,使得点B落在对角线CF上,则阴影部分的面积是 .
5.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
6.如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为 .
7.如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN= .
8.如图,已知正方形ABCD的边长为5,点E、F分别在AD、DC上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
9.如图,四边形ABCD是一个正方形,E是BC延长线上的一点,且AC=EC,则∠E= .
10.如图,在正方形ABCD中,点P是AB上任意一点,PM⊥AC,PN⊥BD,垂足分别为点M、N,若BD=10,则PM+PN= .
11.已知:正方形ABCD的边长为8,点E、F分别在AD、CD上,AE=DF=2,BE与AF相交于点G,点H为BF的中点,连接GH,则GH的长为 .
12.如图,E,F分别是正方形ABCD的边CB,DC延长线上的点,且BE=CF,过点E作EG∥BF,交正方形外角的平分线CG于点G,连接GF.求证:
(1)AE⊥BF;
(2)四边形BEGF是平行四边形.
13.如图,正方形ABCD的对角线AC、BD相交于点O,E是OC上一点,连接EB.过点A作AM⊥BE,垂足为M,AM与BD相交于点F.求证:OE=OF.
14.如图,BD是正方形ABCD的对角线,线段BC在其所在的直线上平移,将平移得到的线段记为PQ,连接PA,过点Q作QO⊥BD,垂足为O,连接OA、OP.
(1)如图①所示,求证:AP=OA;
(2)如图②所示,PQ在BC的延长线上,如图③所示,PQ在BC的反向延长线上,猜想线段AP、OA之间有怎样的数量关系?请直接写出你的猜想,不需证明.
15.如图,正方形ABCD的对角线AC、BD交于点O,∠OCF=∠OBE.求证:∠AEB=∠BFC.
16.如图,在正方形ABCD中,P是对角线BD的一点,点E在AD的延长线上,且PA=PE,PE交CD于点F.
(1)求证:PC=PE;
(2)若PD=DE,求证:BP=BC.
17.如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;
(2)如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
18.(1)如图1,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,求证:EF=BE+FD;
(2)如图2,四边形ABCD中,∠BAD≠90°,AB=AD,∠B+∠D=180°,点E、F分别在边BC、CD上,则当∠EAF与∠BAD满足什么关系时,仍有EF=BE+FD,说明理由.
19.如图,已知四边形ABCD为正方形,AB=3,点E为对角线AC上一动点,连接DE,过点E作EF⊥DE,交BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)求证:矩形DEFG是正方形;
(2)探究:CE+CG的值是否为定值?若是,请求出这个定值;若不是,请说明理由.
20.如图,在矩形ABCD中,AB=16cm,AD=6cm,动点P,Q分别从点A,C同时出发,点P以每秒3cm的速度向点B移动,点Q以每秒2cm测得速度向点D移动,当点P到达点B处时,两点均停止移动
(1)P,Q两点出发多长时间,线段PQ的长度为10cm?
(2)是否存在某一时刻,使四边形PBCQ为正方形?若存在,求出该时刻;若不存在,请说明理由.
参考答案
1.解:A、根据平行四边形的性质得到OA=OC,OB=OD,该结论正确;
B、当AB=CD时,四边形ABCD还是平行四边形,该选项错误;
C、根据有一个角是直角的平行四边形是矩形可以判断该选项正确;
D、当AC=BD且AC⊥BD时,根据对角线相等可判断四边形ABCD是矩形,根据对角线互相垂直可判断四边形ABCD 是菱形,故四边形ABCD是正方形,该结论正确;
故选:B.
2.解:在正方形ABCD中,AB=AD,∠BAD=90°,
在等边△ABE中,AB=AE,∠BAE=∠AEB=60°,
在△ADE中,AD=AE,∠DAE=∠BAD+∠BAE=90°+60°=150°,
所以,∠AED=(180°﹣150°)=15°,
所以∠BED=∠AEB﹣∠AED=60°﹣15°=45°.
故选:C.
3.解:∵四边形ABCD是正方形,
∴∠BOC=90°,∠OBC=45°,
∵BP=OB,
∴∠BOP=∠BPO=(180°﹣45°)=67.5°,
∴∠COP=90°﹣67.5°=22.5°.
故选:B.
4.解:方法一:正方形ABCD的边长为1,将其绕顶点C按逆时针方向旋转一定角度到CEFG位置,使得点B落在对角线CF上,
∴EF=CE=1,
∴CF=,
∴BF=﹣1,
∵∠BFE=45°,
∴阴影部分的面积=×1×1﹣×(﹣1)2=﹣1;
方法二:∵过E点作MN∥BC交AB、CD于M、N点,设AB与EF交于点P点,连接CP,如下图所示,
∵B在对角线CF上,
∴∠DCE=∠ECF=45°,EC=1,
∴△ENC为等腰直角三角形,
∴MB=CN=EC=,
又BC=AD=CD=CE,且CP=CP,△PEC和△PBC均为直角三角形,
∴Rt△PEC≌Rt△PBC(HL),
∴PB=PE,
又∠PFB=45°,
∴∠FPB=45°=∠MPE,
∴△MPE为等腰直角三角形,
设MP=x,则EP=BP=,
∵MP+BP=MB,
∴,解得,
∴BP=,
∴阴影部分的面积=.
故答案为:.
5.解:如图,连接BD交AC于点O,
∵四边形ABCD为正方形,
∴BD⊥AC,OD=OB=OA=OC,
∵AE=CF=2,
∴OA﹣AE=OC﹣CF,即OE=OF,
∴四边形BEDF为平行四边形,且BD⊥EF,
∴四边形BEDF为菱形,
∴DE=DF=BE=BF,
∵AC=BD=8,OE=OF==2,
由勾股定理得:DE===2,
∴四边形BEDF的周长=4DE=4×=8,
故答案为:8.
6.解:如图,过点E作x轴的垂线EH,垂足为H.过点G作x轴的垂线GM,垂足为M,连接GE、FO交于点O′.
∵四边形OEFG是正方形,
∴OG=EO,∠GOM=∠OEH,∠OGM=∠EOH,
在△OGM与△EOH中,
∴△OGM≌△EOH(ASA)
∴GM=OH=2,OM=EH=3,
∴G(﹣3,2).
∴O′(﹣,).
∵点F与点O关于点O′对称,
∴点F的坐标为 (﹣1,5).
故答案是:(﹣1,5).
7.解:连接CF,
∵正方形ABCD和正方形BEFG中,AB=7,BE=5,
∴GF=GB=5,BC=7,
∴GC=GB+BC=5+7=12,
∴=13.
∵M、N分别是DC、DF的中点,
∴MN==.
故答案为:.
8.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
在△ABE和△DAF中,
∵,
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=5、CF=CD﹣DF=5﹣2=3,
∴BF==,
∴GH=BF=,
故答案为:.
9.解:∵四边形ABCD是正方形,
∴∠ACB=45°,AD∥BC,
∵AC=EC,
∴∠E=∠CAE,
∵∠ACB=∠E+∠CAE=2∠E,
∴∠E=∠ACB=22.5°,
故答案为:22.5°.
10.解:在正方形ABCD中,
∴AC⊥BD,∠ABO=45°,
∵PM⊥AC,PN⊥BD,
∴四边形PMON是矩形,
∴PM=ON,
∵PN=BN,
∴PM+PN=ON+BN=OB=BD=5,
故答案为:5
11.解:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=AD,
∵AB=AD,∠BAE=∠D,AE=DF
∴△ABE≌△DAF(SAS),
∴∠ABE=∠DAF,
∵∠ABE+∠BEA=90°,
∴∠DAF+∠BEA=90°,
∴∠AGE=∠BGF=90°,
∵点H为BF的中点,
∴GH=BF,
∵BC=8,CF=CD﹣DF=8﹣2=6
∴BF==10
∴GH=5
故答案为:5
12.证明:(1)∵四边形ABCD是正方形,
∴AB=BC,∠ABC=∠BCD=90°,
∴∠ABE=∠BCF=90°,
在△ABE和△BCF中,,
∴△ABE≌△BCF(SAS),
∴AE=BF,∠BAE=∠CBF,
∵EG∥BF,
∴∠CBF=∠CEG,
∵∠BAE+∠BEA=90°,
∴∠CEG+∠BEA=90°,
∴AE⊥EG,
∴AE⊥BF;
(2)延长AB至点P,使BP=BE,连接EP,如图所示:
则AP=CE,∠EBP=90°,
∴∠P=45°,
∵CG为正方形ABCD外角的平分线,
∴∠ECG=45°,
∴∠P=∠ECG,
由(1)得∠BAE=∠CEG,
在△APE和△ECG中,,
∴△APE≌△ECG(ASA),
∴AE=EG,
∵AE=BF,
∴EG=BF,
∵EG∥BF,
∴四边形BEGF是平行四边形.
13.证明:∵四边形ABCD是正方形.
∴∠BOE=∠AOF=90°,OB=OA.
又∵AM⊥BE,
∴∠MEA+∠MAE=90°=∠AFO+∠MAE,
∴∠MEA=∠AFO.
∴△BOE≌△AOF(AAS).
∴OE=OF.
14.(1)证明:∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,
∴∠BOQ=90°,
∴∠BQO=∠CBD=45°,
∴OB=OQ,
∵PQ=BC,
∴AB=PQ,
在△ABO和△PQO中,,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,
∴∠BOP+∠AOB=90,即∠AOP=90°,
∴△AOP是等腰直角三角形,
∴AP=OA;
(2)解:PQ在BC的延长线上,线段AP、OA之间的数量关系为:AP=OA;理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,
∴∠BOQ=90°,
∴∠BQO=∠CBD=45°,
∴OB=OQ,
∵PQ=BC,
∴AB=PQ,
在△ABO和△PQO中,,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP+∠POQ=90°,
∴∠BOP+∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,
∴AP=OA;
PQ在BC的反向延长线上,线段AP、OA之间的数量关系为:AP=OA;理由如下:
∵四边形ABCD是正方形,
∴AB=BC,∠ABD=∠CBD=45°,
∵QO⊥BD,
∴∠BOQ=90°,
∴∠BQO=∠CBD=∠OBQ=45°,
∴OB=OQ,∠ABO=∠PQO=135°,
∵PQ=BC,
∴AB=PQ,
在△ABO和△PQO中,,
∴△ABO≌△PQO(SAS),
∴OA=OP,∠AOB=∠POQ,
∵∠BOP﹣∠POQ=90°,
∴∠BOP﹣∠AOB=90°,即∠AOP=90°,
∴△AOP是等腰直角三角形,
∴AP=OA.
15.证明:∵四边形ABCD是正方形,
∴AC⊥BD,即∠AOB=∠BOC=90°,
∴OB=OC,
在△OCF和△OBE中,
,
∴△OCF≌△OBE(ASA),
∴∠OFC=∠OEB,
∴∠BFC=∠AEB.
16.(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠ADP=∠CDP,
在△ADP和△CDP中,
,
∴△ADP≌△CDP(SAS),
∴PA=PC,
∵PA=PE,
∴PC=PE.
(2)证明:四边形ABCD为正方形,
∴∠ADC=∠CDE=90°,
∴∠E+∠DFE=90°,
∵PA=PE,
∴∠PAD=∠E,
由(1)知△ADP≌△CDP,
∴∠PAD=∠PCD,
∴∠PCD=∠E,
∵∠PFC=∠DFE,
∴∠PCD+∠PFC=∠E+∠DFE=90°,
∴∠CPE=90°,
∴∠BPC+∠DPE=90°,
∵PD=DE,
∴∠DPE=∠E,
∴∠DPE=∠PCD,
∵∠BCP+∠PCD=90°,
∴∠BPC=∠BCP,
∴BP=BC.
17.解:(1)结论:PB=PQ,
理由:如图①中,过P作PE⊥BC,PF⊥CD,垂足分别为E,F.
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形.
∵∠BPE+∠QPE=90°,∠QPE+∠QPF=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ;
(2)结论:PB=PQ.
理由:如图②,过P作PE⊥BC,PF⊥CD,垂足分别为E,F,
∵P为正方形对角线AC上的点,
∴PC平分∠DCB,∠DCB=90°,
∴PF=PE,
∴四边形PECF为正方形,
∵∠BPF+∠QPF=90°,∠BPF+∠BPE=90°,
∴∠BPE=∠QPF,
在△PQF和△PBE中,
,
∴Rt△PQF≌Rt△PBE,
∴PB=PQ.
18.证明:(1)如图1:把△ABE绕点A逆时针旋转90°至△ADG,
则△ADG≌△ABE,
∴AG=AE,∠DAG=∠BAE,DG=BE,
又∵∠EAF=45°,即∠DAF+∠BEA=∠EAF=45°,
∴∠GAF=∠FAE,
在△GAF和△EAF中,
,
∴△GAF≌△EAF(SAS).
∴GF=EF.
又∵DG=BE,
∴GF=BE+DF,
∴BE+DF=EF;
(2)当∠BAD=2∠EAF时,仍有EF=BE+FD,
理由如下:如图2,延长CB至M,使BM=DF,连接AM,
∵∠ABC+∠D=180°,∠ABC+∠ABM=180°,
∴∠D=∠ABM,
在△ABM和△ADF中,
,
∴△ABM≌△ADF(SAS)
∴AF=AM,∠DAF=∠BAM,
∵∠BAD=2∠EAF,
∴∠DAF+∠BAE=∠EAF,
∴∠EAB+∠BAM=∠EAM=∠EAF,
在△FAE和△MAE中,
,
∴△FAE≌△MAE(SAS),
∴EF=EM=BE+BM=BE+DF,
即EF=BE+DF.
19.解:(1)如图,作EM⊥BC于M,EN⊥CD于N,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
(2)CE+CG的值是定值,定值为6,理由如下:
∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在∴△ADE和△CDG中,,
∴△ADE≌△CDG(SAS),
∴AE=CG,
∴CE+CG=CE+AE=AC=AB=×3=6是定值.
20.解:(1)过点P作PH⊥CD于点H,
∴HQ=16﹣5t,
∴PQ2=PH2+HQ2,
即102=(16﹣5t)2+62,
解得:,
答:P,Q两点出发或秒,线段PQ的长度为10cm;
(2)假设四边形PBCQ是正方形,
∴BP=CQ,即16﹣3t=2t,
解得:t=,
∵,
∴不成立.
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
