1.3 反比例函数的应用 课件(共21张PPT)
文档属性
| 名称 | 1.3 反比例函数的应用 课件(共21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 00:00:00 | ||
图片预览






文档简介
第一章 反比例函数
3 反比例函数的应用
知识点一 反比例函数的实际应用
1.利用反比例函数解决实际问题时,首先要建立反比例函数的数学模型,这也是关键的一步.一般地,建立反比例函数模型有两种思路:
(1)题目中明确指出变量间存在反比例函数关系时,可利用待定系数法求反比例函数的关系式.
(2)题目中未指出变量间存在反比例函数关系时,可利用基本数量关系求解反比例函数的关系式.
2.反比例函数模型建立后,便可以利用反比例函数的图象及性质解决问题一般地,可归结为以下两种情况:
(1)已知一变量的取值,求另一变量的对应值:在两个变量中,已知其中一个变量的取值,代入反比例函数的关系式便可以求出另一变量的值.
(2)已知一变量的取值范围,求另一变量对应的取值范围:
①利用方程求解:在两变量中,已知其中一个变量的取值范围,当取值范围有两端点值时,将取值范围的两端点值分别代入反比例函数的关系式,便可得到另一变量的取值范围;当取值范围只有一个端点值时,将取值范围的端点值代入关系式,得到另一变量的对应值,再借助函数的图象或性质得到另一变量的取值范围.
②利用不等式直接求解.
温馨提示
(1)建立反比例函数模型与建立方程及其他函数模型类似,关键是分析各个量之间的关系,找到变量间的相等关系,列出变量之间的关系式,进而转化成函数模型.
(2)实际问题中的反比例函数,自变量的取值(范围)往往会受到限制,这时所对应的函数图象是双曲线的一支或双曲线的一支中的一段.
温馨提示
(1)建立反比例函数模型与建立方程及其他函数模型类似,关键是分析各个量之间的关系,找到变量间的相等关系,列出变量之间的关系式,进而转化成函数模型.
(2)实际问题中的反比例函数,自变量的取值(范围)往往会受到限制,这时所对应的函数图象是双曲线的一支或双曲线的一支中的一段.
易错警示
在实际问题中,已知其中一个变量的取值范围求另一变量的取值范围时,要注意两变量之间的反比例关系.
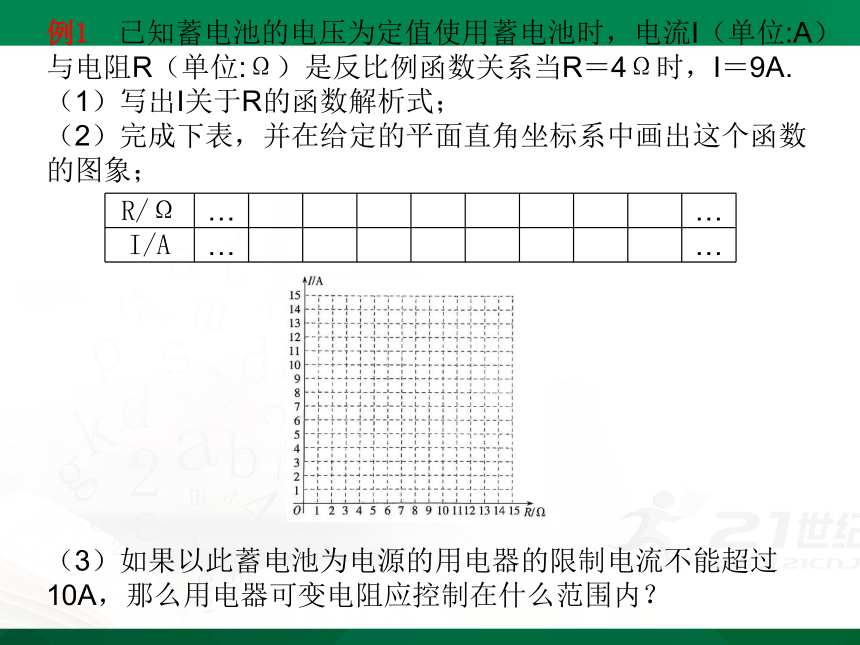
例1 已知蓄电池的电压为定值使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系当R=4Ω时,I=9A.
(1)写出I关于R的函数解析式;
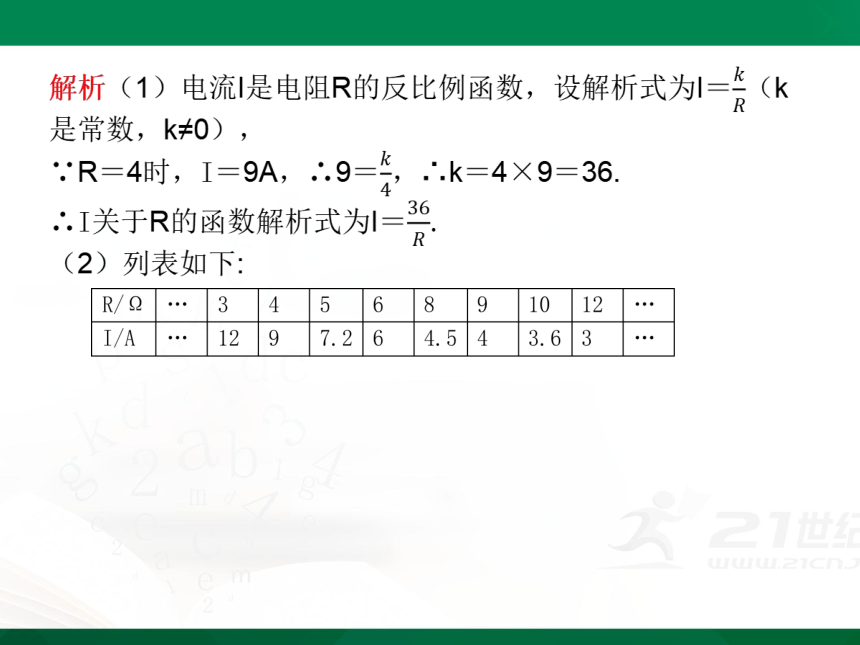
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
R/Ω
…
…
I/A
…
…
(3)如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围内?
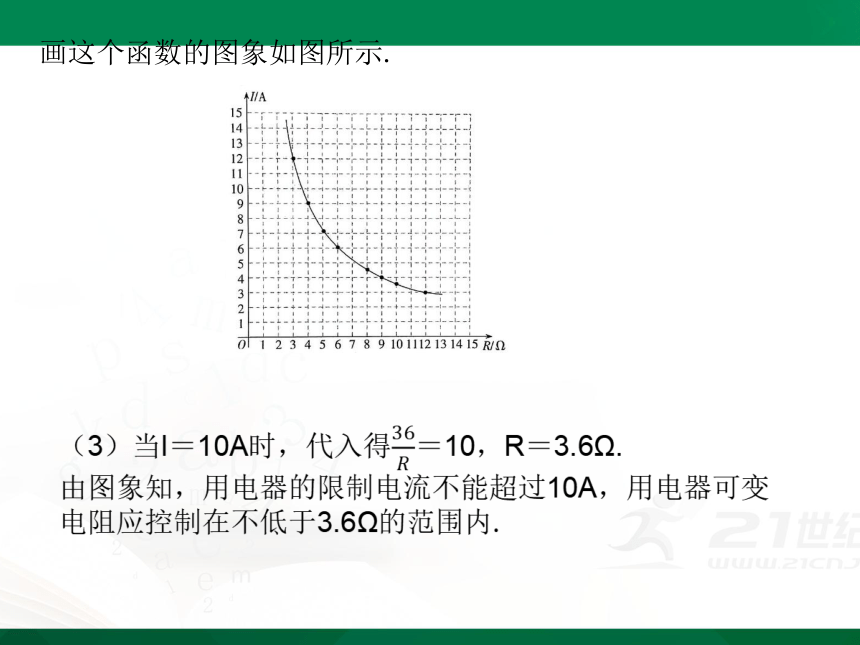
画这个函数的图象如图所示.
温馨提示
已知双曲线上一点的坐标,利用待定系数法即可求得比例系数k的值及反比例函数的表达式,进一步利用表达式即可求出变量的值.
知识点二 反比例函数与一次函数的综合应用
1.反比例函数与正比例函数的综合应用
反比例函数与正比例函数的区别与联系:
正比例函数
反比例函数
区别
定义
y=kx(k是常数,且k≠0)
(k是常数,且k≠0)
自变量的指数
1
-1
自变量的取值范围
全体实数
不等于0的全体实数
图象
经过原点的直线
双曲线
增减性
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小
当k>0时,在每个象限内,y随x的增大而减小;当k<0时,在每个象限内,y随x的增大而增大
联系
①两函数的图象都关于原点对称;②两函数的图象都经过点(1,k);③当k>0时,两函数的图象都过(在)第一、三象限;当k<0时,两函数的图象都过(在)第二、四象限;④两函数中都只有一个待定系数,因此确定表达式时,都只需要一对x、y的对应值.
例2 已知正比例函数y1的图象与反比例函数y2的图象相交于点A(-2,4),下列说法正确的是( )
A.正比例函数y1的解析式是y1=2x
B.两个函数图象的另一交点坐标为(4,-2)
C.正比例函数y1与反比例函数y2都随x的增大而增大
D.当x<-2或0<x<2时,y2<y1
例2 已知正比例函数y1的图象与反比例函数y2的图象相交于点A(-2,4),下列说法正确的是( )
A.正比例函数y1的解析式是y1=2x
B.两个函数图象的另一交点坐标为(4,-2)
C.正比例函数y1与反比例函数y2都随x的增大而增大
D.当x<-2或0<x<2时,y2<y1
答案 D
2.反比例函数与一次函数的综合应用
反比例函数与一次函数综合应用的情况
解决对策
已知反比例函数图象与一次函数图象的一个交点坐标,求两函数的表达式,进而求另一交点的坐标
用待定系数法求两函数表达式,进一步联立两函数表达式,组成方程组,解之便可求得另一交点的坐标
根据两函数的大小关系求自变量的取值范围
借助图象的直观性解决,并以两交点及y轴为分界,分四种情况讨论
经典例题
题型 反比例函数与一次函数的综合题
(1)求该一次函数的解析式;
(2)求△AOB的面积.
方法技巧
解决此类题常用到三种技巧:一是待定系数法求两函数表达式;二是将不易求解的图形面积问题转化为其他图形面积的和、差问题;三是利用点的坐标表示线段长度,进而求解图形的面积.
3 反比例函数的应用
知识点一 反比例函数的实际应用
1.利用反比例函数解决实际问题时,首先要建立反比例函数的数学模型,这也是关键的一步.一般地,建立反比例函数模型有两种思路:
(1)题目中明确指出变量间存在反比例函数关系时,可利用待定系数法求反比例函数的关系式.
(2)题目中未指出变量间存在反比例函数关系时,可利用基本数量关系求解反比例函数的关系式.
2.反比例函数模型建立后,便可以利用反比例函数的图象及性质解决问题一般地,可归结为以下两种情况:
(1)已知一变量的取值,求另一变量的对应值:在两个变量中,已知其中一个变量的取值,代入反比例函数的关系式便可以求出另一变量的值.
(2)已知一变量的取值范围,求另一变量对应的取值范围:
①利用方程求解:在两变量中,已知其中一个变量的取值范围,当取值范围有两端点值时,将取值范围的两端点值分别代入反比例函数的关系式,便可得到另一变量的取值范围;当取值范围只有一个端点值时,将取值范围的端点值代入关系式,得到另一变量的对应值,再借助函数的图象或性质得到另一变量的取值范围.
②利用不等式直接求解.
温馨提示
(1)建立反比例函数模型与建立方程及其他函数模型类似,关键是分析各个量之间的关系,找到变量间的相等关系,列出变量之间的关系式,进而转化成函数模型.
(2)实际问题中的反比例函数,自变量的取值(范围)往往会受到限制,这时所对应的函数图象是双曲线的一支或双曲线的一支中的一段.
温馨提示
(1)建立反比例函数模型与建立方程及其他函数模型类似,关键是分析各个量之间的关系,找到变量间的相等关系,列出变量之间的关系式,进而转化成函数模型.
(2)实际问题中的反比例函数,自变量的取值(范围)往往会受到限制,这时所对应的函数图象是双曲线的一支或双曲线的一支中的一段.
易错警示
在实际问题中,已知其中一个变量的取值范围求另一变量的取值范围时,要注意两变量之间的反比例关系.
例1 已知蓄电池的电压为定值使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系当R=4Ω时,I=9A.
(1)写出I关于R的函数解析式;
(2)完成下表,并在给定的平面直角坐标系中画出这个函数的图象;
R/Ω
…
…
I/A
…
…
(3)如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围内?
画这个函数的图象如图所示.
温馨提示
已知双曲线上一点的坐标,利用待定系数法即可求得比例系数k的值及反比例函数的表达式,进一步利用表达式即可求出变量的值.
知识点二 反比例函数与一次函数的综合应用
1.反比例函数与正比例函数的综合应用
反比例函数与正比例函数的区别与联系:
正比例函数
反比例函数
区别
定义
y=kx(k是常数,且k≠0)
(k是常数,且k≠0)
自变量的指数
1
-1
自变量的取值范围
全体实数
不等于0的全体实数
图象
经过原点的直线
双曲线
增减性
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小
当k>0时,在每个象限内,y随x的增大而减小;当k<0时,在每个象限内,y随x的增大而增大
联系
①两函数的图象都关于原点对称;②两函数的图象都经过点(1,k);③当k>0时,两函数的图象都过(在)第一、三象限;当k<0时,两函数的图象都过(在)第二、四象限;④两函数中都只有一个待定系数,因此确定表达式时,都只需要一对x、y的对应值.
例2 已知正比例函数y1的图象与反比例函数y2的图象相交于点A(-2,4),下列说法正确的是( )
A.正比例函数y1的解析式是y1=2x
B.两个函数图象的另一交点坐标为(4,-2)
C.正比例函数y1与反比例函数y2都随x的增大而增大
D.当x<-2或0<x<2时,y2<y1
例2 已知正比例函数y1的图象与反比例函数y2的图象相交于点A(-2,4),下列说法正确的是( )
A.正比例函数y1的解析式是y1=2x
B.两个函数图象的另一交点坐标为(4,-2)
C.正比例函数y1与反比例函数y2都随x的增大而增大
D.当x<-2或0<x<2时,y2<y1
答案 D
2.反比例函数与一次函数的综合应用
反比例函数与一次函数综合应用的情况
解决对策
已知反比例函数图象与一次函数图象的一个交点坐标,求两函数的表达式,进而求另一交点的坐标
用待定系数法求两函数表达式,进一步联立两函数表达式,组成方程组,解之便可求得另一交点的坐标
根据两函数的大小关系求自变量的取值范围
借助图象的直观性解决,并以两交点及y轴为分界,分四种情况讨论
经典例题
题型 反比例函数与一次函数的综合题
(1)求该一次函数的解析式;
(2)求△AOB的面积.
方法技巧
解决此类题常用到三种技巧:一是待定系数法求两函数表达式;二是将不易求解的图形面积问题转化为其他图形面积的和、差问题;三是利用点的坐标表示线段长度,进而求解图形的面积.
