北京市朝阳区2020-2021学年高一下学期期末考试数学试题(word版,含答案)
文档属性
| 名称 | 北京市朝阳区2020-2021学年高一下学期期末考试数学试题(word版,含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 366.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 00:00:00 | ||
图片预览



文档简介
北京市朝阳区2020-2021学年高一下学期期末考试
数
学
2021.7
(考试时间120分钟
满分150分)
本试卷分为选择题(共50分)和非选择提(共100分)两部分
第一部分(选择题
共50分)
一、选择题(本大题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项)
(1)已知复数(其中i是虚数单位),则z在复平面内对应的点的坐标是
(A)(1,1)
(B)(1,-1)
(C)(-1,1)
(D)(-1,-1)
(2)如图、在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,若AB=PD=3,AD=2,则该四棱锥的体积为
(A)18
(B)12
(C)9
(D)6
(3)一个袋子中有大小和质地相同的4个球,其中有2个红色球,2个绿色球,从袋中不放回地依次随机摸出2个球,则两个球颜色相同的概率是
(A)
(B)
(C)
(D)
(4)设α,β是两个不同的平面,n是平面α内的一条直线,则“n⊥β”是“α⊥β”的
(A)充分不必要条件
(B)必要不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
(5)在△ABC中,,则∠A=
(A)
(B)
(C)
(D)
(6)水稻是世界最重要的食作物之一,也是我国60%以上人口的主粮。以袁隆平院士为首的科学家研制成功的杂交水稻制种技术在世界上被誉为中国的“第五大发明",育种技术的突破,杂交水稻的推广,不仅让中国人端稳饭碗,也为解决世界粮食短缺问题作出了巨大贡献.某农场种植的甲、乙两种水稻在面积相等的两块稻田中连续6年的产量(单位:kg)如下:
品种
第1年
第2年
第3年
第4年
第5年
第6年
甲
900
920
900
850
910
920
乙
890
960
950
850
860
890
根据以上数据,下面说法正确的是
(A)甲种水稻产量的平均数比乙种水稻产量的平均数大
(B)甲种水稻产量的中位数比乙种水稻产量的中位数小
(C)甲种水稻产量的极差与乙种水稻产量的极差相等
(D)甲种水稻的产量比乙种水稻的产量稳定
(7)向量在正方形网格中的位置如图所示,若,则=
(A)3
(B)
(C)-3
(D)
(8)某中学举办知识竞赛,共50人参加初试,成绩如下:
成绩(分)
95
90
85
80
75
70
65
60
60以下
人数
1
4
6
5
4
6
7
8
9
如果有40%的学生可以参加复试,则进入复试的分数线可以为
(A)65
(B)70
(C)75
(D)80
(9)在棱长为1的正方体中,若点E是核AB的中点,点M是底面ABCD内的动点,且满足,则线段AM的长的最小值为
(A)
(B)
(C)1
(D)
(10)已知不共线的平面向量a,b,c两两的夹角相等,且,实数,,则的最大值为
(A)
(B)2
(C)
(D)5
第二部分(非选择题
共100分)
二、填空题(本大题共6小题,每小题5分,共30分)
(11)已知平面向量a=(2,k),b=(3,2),且a⊥b,则实数k=_______________.
(12)若复数为纯虚数,则实数a的值为_______________.
(13)某班有42名学生,其中选考物理的学生有21人,选考地理的学生有14人,选考物理或地理的学生有28人,从该班任选一名学生,则该生既选考物理又选考地理的概率为_______________.
(14)已知一组不全相等的样本数据的平均数为10,方差为2,现再加入一个新数10,则新样本数据的平均数____________,方差____________.(填“变大”,“变小”,“不变”)
(15)已知等边△ABC的边长为2,D为边BC的中点,点M是AC边上的动点,则的最大值为______________,最小值为______________.
(16)已知△ABC的三边长为连续的正整数,给出下列四个结论:
①存在满足条件的三角形,使得三个内角中的最大角等于另外两个角的和;
②存在满足条件的三角形,使得三个内角中的最大角大于另外两个角的和;
③存在满足条件的三角形,使得三个内角中的最大角等于最小角的2倍;
④存在满足条件的三角形,使得三个内角中的最大角等于最小角的3倍.
其中所有正确结论的序号是_____________.
三、解答题(本大题共5小题,共70分。解答应写出文字说明,演算步骤或明过过程)
(17)(本小题14分)
在△ABC中,
(Ⅰ)求cosA的值;
(Ⅱ)若B=2A,,求a的值.
(18)(本小题14分)
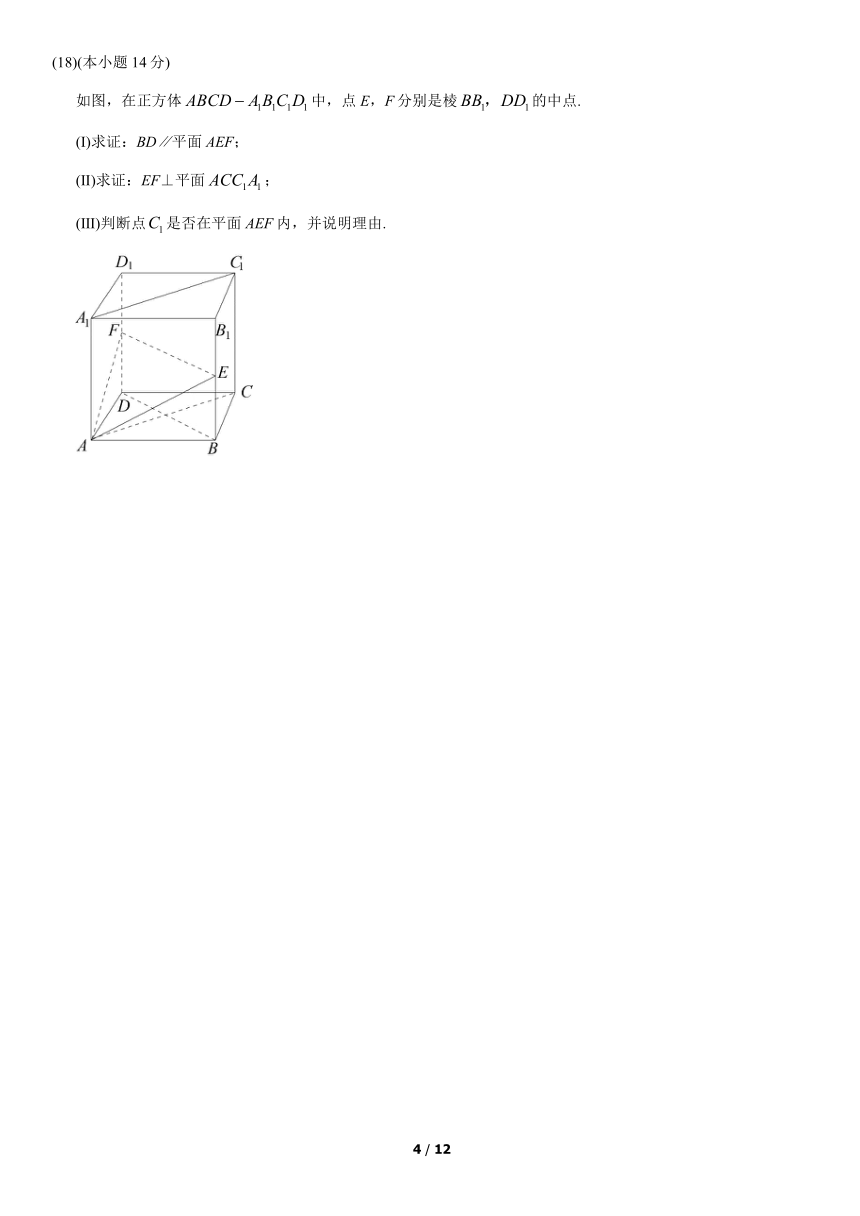
如图,在正方体中,点E,F分别是棱的中点.
(Ⅰ)求证:BD∥平面AEF;
(Ⅱ)求证:EF⊥平面;
(Ⅲ)判断点是否在平面AEF内,并说明理由.
(19)(本小题14分)
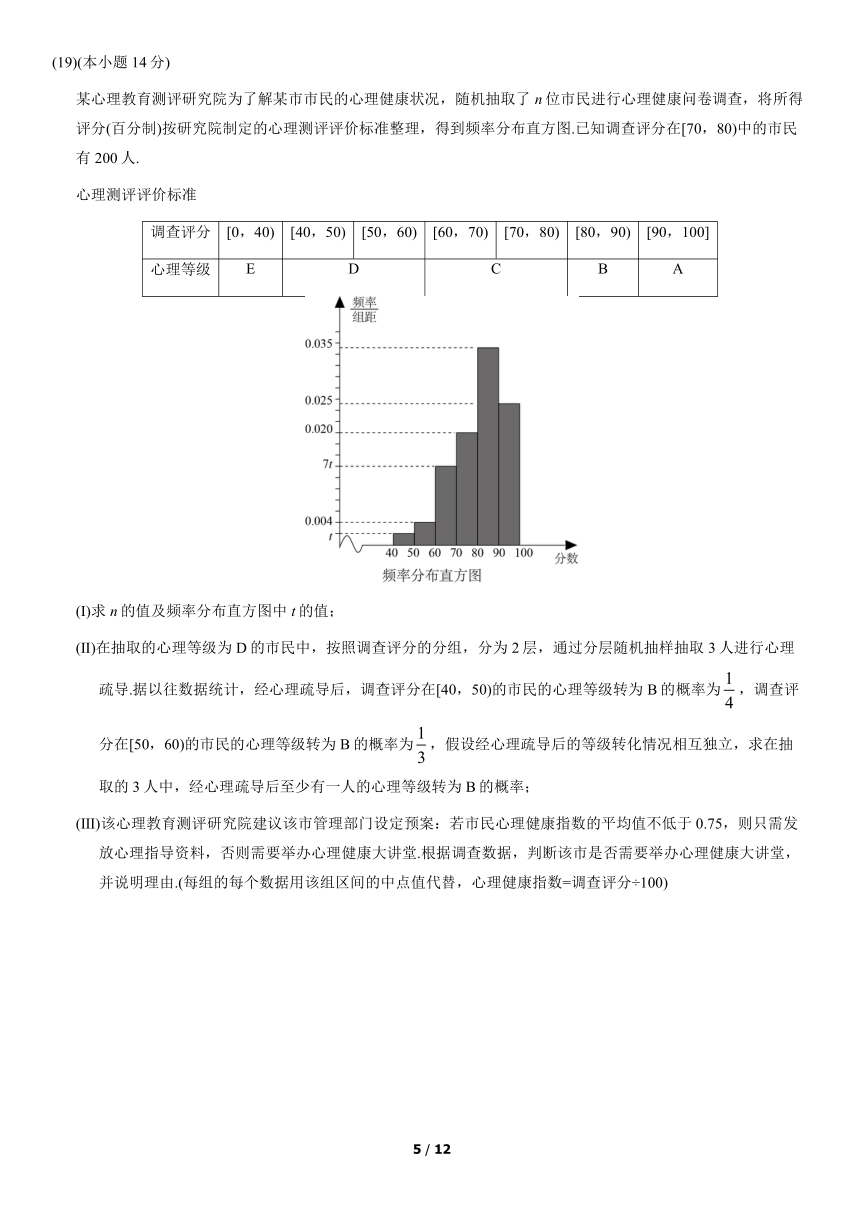
某心理教育测评研究院为了解某市市民的心理健康状况,随机抽取了n位市民进行心理健康问卷调查,将所得评分(百分制)按研究院制定的心理测评评价标准整理,得到频率分布直方图.已知调查评分在[70,80)中的市民有200人.
心理测评评价标准
调查评分
[0,40)
[40,50)
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
心理等级
E
D
C
B
A
(Ⅰ)求n的值及频率分布直方图中t的值;
(Ⅱ)在抽取的心理等级为D的市民中,按照调查评分的分组,分为2层,通过分层随机抽样抽取3人进行心理疏导.据以往数据统计,经心理疏导后,调查评分在[40,50)的市民的心理等级转为B的概率为,调查评分在[50,60)的市民的心理等级转为B的概率为,假设经心理疏导后的等级转化情况相互独立,求在抽取的3人中,经心理疏导后至少有一人的心理等级转为B的概率;
(Ⅲ)该心理教育测评研究院建议该市管理部门设定预案:若市民心理健康指数的平均值不低于0.75,则只需发放心理指导资料,否则需要举办心理健康大讲堂.根据调查数据,判断该市是否需要举办心理健康大讲堂,并说明理由.(每组的每个数据用该组区间的中点值代替,心理健康指数=调查评分÷100)
(20)(本小题14分)
如图,在锐角△ABC中,,D,E分别是边AB,AC上的点.且DE=2.再从条件①、条件②、条件③中选择两个能解决下面问题的条件作为已知,并求,
(Ⅰ)sinC的值;
(Ⅱ)∠BDE的大小;
(Ⅲ)四边形BCED的面积.
条件①:;
条件②:;
条件③:EC=3.
(21)(本小题14分)
将平面直角坐标系中的一列点记为,设,其中j为与y轴方向相同的单位向量.若对任意的正整数n,都有f(n+1)>f(n),则称为T点列.
(Ⅰ)判断是否为T点列,并说明理由;
(Ⅱ)若为T点列,且.任取其中连续三点,证明△为钝角三角形;
(Ⅲ)若为T点列,对于正整数k,l,m(k北京市朝阳区2020-2021学年高一下学期期末考试数学试题
参考答案
一、选择题(共10小题,莓小题5分,共50分)
(1)B
(2)D
(3)B
(4)A
(5)C
(6)D
(7)D
(8)C
(9)B
(10)C
二、填空题(共6小题,每小题5分,共30分)
(11)-3
(12)-2
(13)
(14)不变;变小
(15)3;
(16)①②③
三、解答题(共5小题,共70分
(17)(共14分)
解:(Ⅰ)因为在△ABC中,
又因为
所以·····································6分
(Ⅱ)由(Ⅰ)知,,
所以
因为B=2A,
所以
又因为
所以·····································14分
(18)(共14分)
解:(Ⅰ)因为在正方体中,点E,F分别是棱的中点.
所以BE//DF,BE=DF
所以四边形BEFD为平行四边形,所以BD//EF
又因为平面平面AEF,
所以BD//平面AEF·····································5分
(Ⅱ)因为在正方体中,平面ABCD,
所以.
因为四边形ABCD为正方形,所以AC⊥BD
又由(Ⅰ)知BD//EF,
所以
又因为,
所以EF⊥平面····································10分
(Ⅲ)点在平面AEF内,理由如下:
取中点G,连接,
因为在正方体中,点G,F分别是棱的中点,
所以DF//CG,DF=CG.
所以四边形DCGF为平行四边形.所以FG//DC,FG=DC.
又因为AB//DC,AB=DC,
所以AB//FG,AB=FG.
所以四边形ABGF为平行四边形.所以AF//BG.
因为在正方体中,点E,G分别是棱的中点,
所以.
所以四边形为平行四边形.所以.
所以.
故点在平面AEF内.
···································14分
(19)(共14分)
解:(Ⅰ)由已知条件可得,又因为每组的小矩形的面职之和为1.
所以(0.035+0.025+0.02+0.004+8t)×10=1,解得t=0.002···································4分
(Ⅱ)由(Ⅰ)知:t=0.002,
所以调查评分在[40,50)中的人数是调查评分在[50,60)中人数的,
若按分层抽样抽取3人,则调查评分在[40,50)中有1人,在[50,60)中有2人,
设事件M=“在抽取的3人中,经心理疏导后至少有一人的心理等级转为B”.
因为经心理疏导后的等级转化情况相互独立,
所以
所以
故经心理疏导后至少有一人的心理等级转为B的概率为···································10分
(Ⅲ)由频率分布直方图可得,
45×0.02+55×0.04+65×0.14+75×0.2+85×0.35+95×0.25=80.7.
估计市民心理健康调查评分的平均值为80.7,
所以市民心理健康指数平均值为.
所以只需发放心理指导材料,不需要举办心理健康大讲堂活动.
···································14分
(20)(共14分)
解:选条件__①__,__③__
(Ⅰ)因为
又因为在中,,
所以···································4分
(II)因为△ABC是锐角三角形,由(Ⅰ)知
所以
在△ABC中,因为,
所以即,解得AC=5.
又因为EC=3,所以AE=2.
又因为DE=2,所以.故···································10分
(Ⅲ)因为,由(Ⅱ)知AC=5,
所以
又因为
所以
所以四边形BCED的面积为···································14分
选条件__②__,__③__.
(Ⅰ)因为
所以
所以
···································4分
(Ⅱ)由(Ⅰ)及正弦定理:得
又因为EC=3,所以AE=2,
又因为DE=2,所以故···································10分
(Ⅲ)因为△ABC是锐角三角形,由(Ⅰ)知
所以
由余弦定理得:
解得:.
所以
又因为
所以
所以四边形BCED的面积为···································14分
(21)(共14分)
解:(Ⅰ)为T点列.理由如下:
由题意可知,
所以
即f(n+1)>f(n),n=1,2,….
所以为T点列.
···································4分
(Ⅱ)由题意可知,
所以
因为为T点列,
所以
又因为,所以.
所以对中连续三点,都有
又
所以所以为.的最大内角
由余弦定理得:
故为钝角,所以为钝角三角形.
···································10分
(Ⅲ)由k因为为T点列,由(Ⅱ)知
所以
······
两边分别相加可得
所以,
所以
所以
又
所以,
所以···································14分
7
/
12
数
学
2021.7
(考试时间120分钟
满分150分)
本试卷分为选择题(共50分)和非选择提(共100分)两部分
第一部分(选择题
共50分)
一、选择题(本大题共10小题,每小题5分,共50分。在每小题列出的四个选项中,选出符合题目要求的一项)
(1)已知复数(其中i是虚数单位),则z在复平面内对应的点的坐标是
(A)(1,1)
(B)(1,-1)
(C)(-1,1)
(D)(-1,-1)
(2)如图、在四棱锥P-ABCD中,底面ABCD为矩形,PD⊥底面ABCD,若AB=PD=3,AD=2,则该四棱锥的体积为
(A)18
(B)12
(C)9
(D)6
(3)一个袋子中有大小和质地相同的4个球,其中有2个红色球,2个绿色球,从袋中不放回地依次随机摸出2个球,则两个球颜色相同的概率是
(A)
(B)
(C)
(D)
(4)设α,β是两个不同的平面,n是平面α内的一条直线,则“n⊥β”是“α⊥β”的
(A)充分不必要条件
(B)必要不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
(5)在△ABC中,,则∠A=
(A)
(B)
(C)
(D)
(6)水稻是世界最重要的食作物之一,也是我国60%以上人口的主粮。以袁隆平院士为首的科学家研制成功的杂交水稻制种技术在世界上被誉为中国的“第五大发明",育种技术的突破,杂交水稻的推广,不仅让中国人端稳饭碗,也为解决世界粮食短缺问题作出了巨大贡献.某农场种植的甲、乙两种水稻在面积相等的两块稻田中连续6年的产量(单位:kg)如下:
品种
第1年
第2年
第3年
第4年
第5年
第6年
甲
900
920
900
850
910
920
乙
890
960
950
850
860
890
根据以上数据,下面说法正确的是
(A)甲种水稻产量的平均数比乙种水稻产量的平均数大
(B)甲种水稻产量的中位数比乙种水稻产量的中位数小
(C)甲种水稻产量的极差与乙种水稻产量的极差相等
(D)甲种水稻的产量比乙种水稻的产量稳定
(7)向量在正方形网格中的位置如图所示,若,则=
(A)3
(B)
(C)-3
(D)
(8)某中学举办知识竞赛,共50人参加初试,成绩如下:
成绩(分)
95
90
85
80
75
70
65
60
60以下
人数
1
4
6
5
4
6
7
8
9
如果有40%的学生可以参加复试,则进入复试的分数线可以为
(A)65
(B)70
(C)75
(D)80
(9)在棱长为1的正方体中,若点E是核AB的中点,点M是底面ABCD内的动点,且满足,则线段AM的长的最小值为
(A)
(B)
(C)1
(D)
(10)已知不共线的平面向量a,b,c两两的夹角相等,且,实数,,则的最大值为
(A)
(B)2
(C)
(D)5
第二部分(非选择题
共100分)
二、填空题(本大题共6小题,每小题5分,共30分)
(11)已知平面向量a=(2,k),b=(3,2),且a⊥b,则实数k=_______________.
(12)若复数为纯虚数,则实数a的值为_______________.
(13)某班有42名学生,其中选考物理的学生有21人,选考地理的学生有14人,选考物理或地理的学生有28人,从该班任选一名学生,则该生既选考物理又选考地理的概率为_______________.
(14)已知一组不全相等的样本数据的平均数为10,方差为2,现再加入一个新数10,则新样本数据的平均数____________,方差____________.(填“变大”,“变小”,“不变”)
(15)已知等边△ABC的边长为2,D为边BC的中点,点M是AC边上的动点,则的最大值为______________,最小值为______________.
(16)已知△ABC的三边长为连续的正整数,给出下列四个结论:
①存在满足条件的三角形,使得三个内角中的最大角等于另外两个角的和;
②存在满足条件的三角形,使得三个内角中的最大角大于另外两个角的和;
③存在满足条件的三角形,使得三个内角中的最大角等于最小角的2倍;
④存在满足条件的三角形,使得三个内角中的最大角等于最小角的3倍.
其中所有正确结论的序号是_____________.
三、解答题(本大题共5小题,共70分。解答应写出文字说明,演算步骤或明过过程)
(17)(本小题14分)
在△ABC中,
(Ⅰ)求cosA的值;
(Ⅱ)若B=2A,,求a的值.
(18)(本小题14分)
如图,在正方体中,点E,F分别是棱的中点.
(Ⅰ)求证:BD∥平面AEF;
(Ⅱ)求证:EF⊥平面;
(Ⅲ)判断点是否在平面AEF内,并说明理由.
(19)(本小题14分)
某心理教育测评研究院为了解某市市民的心理健康状况,随机抽取了n位市民进行心理健康问卷调查,将所得评分(百分制)按研究院制定的心理测评评价标准整理,得到频率分布直方图.已知调查评分在[70,80)中的市民有200人.
心理测评评价标准
调查评分
[0,40)
[40,50)
[50,60)
[60,70)
[70,80)
[80,90)
[90,100]
心理等级
E
D
C
B
A
(Ⅰ)求n的值及频率分布直方图中t的值;
(Ⅱ)在抽取的心理等级为D的市民中,按照调查评分的分组,分为2层,通过分层随机抽样抽取3人进行心理疏导.据以往数据统计,经心理疏导后,调查评分在[40,50)的市民的心理等级转为B的概率为,调查评分在[50,60)的市民的心理等级转为B的概率为,假设经心理疏导后的等级转化情况相互独立,求在抽取的3人中,经心理疏导后至少有一人的心理等级转为B的概率;
(Ⅲ)该心理教育测评研究院建议该市管理部门设定预案:若市民心理健康指数的平均值不低于0.75,则只需发放心理指导资料,否则需要举办心理健康大讲堂.根据调查数据,判断该市是否需要举办心理健康大讲堂,并说明理由.(每组的每个数据用该组区间的中点值代替,心理健康指数=调查评分÷100)
(20)(本小题14分)
如图,在锐角△ABC中,,D,E分别是边AB,AC上的点.且DE=2.再从条件①、条件②、条件③中选择两个能解决下面问题的条件作为已知,并求,
(Ⅰ)sinC的值;
(Ⅱ)∠BDE的大小;
(Ⅲ)四边形BCED的面积.
条件①:;
条件②:;
条件③:EC=3.
(21)(本小题14分)
将平面直角坐标系中的一列点记为,设,其中j为与y轴方向相同的单位向量.若对任意的正整数n,都有f(n+1)>f(n),则称为T点列.
(Ⅰ)判断是否为T点列,并说明理由;
(Ⅱ)若为T点列,且.任取其中连续三点,证明△为钝角三角形;
(Ⅲ)若为T点列,对于正整数k,l,m(k
参考答案
一、选择题(共10小题,莓小题5分,共50分)
(1)B
(2)D
(3)B
(4)A
(5)C
(6)D
(7)D
(8)C
(9)B
(10)C
二、填空题(共6小题,每小题5分,共30分)
(11)-3
(12)-2
(13)
(14)不变;变小
(15)3;
(16)①②③
三、解答题(共5小题,共70分
(17)(共14分)
解:(Ⅰ)因为在△ABC中,
又因为
所以·····································6分
(Ⅱ)由(Ⅰ)知,,
所以
因为B=2A,
所以
又因为
所以·····································14分
(18)(共14分)
解:(Ⅰ)因为在正方体中,点E,F分别是棱的中点.
所以BE//DF,BE=DF
所以四边形BEFD为平行四边形,所以BD//EF
又因为平面平面AEF,
所以BD//平面AEF·····································5分
(Ⅱ)因为在正方体中,平面ABCD,
所以.
因为四边形ABCD为正方形,所以AC⊥BD
又由(Ⅰ)知BD//EF,
所以
又因为,
所以EF⊥平面····································10分
(Ⅲ)点在平面AEF内,理由如下:
取中点G,连接,
因为在正方体中,点G,F分别是棱的中点,
所以DF//CG,DF=CG.
所以四边形DCGF为平行四边形.所以FG//DC,FG=DC.
又因为AB//DC,AB=DC,
所以AB//FG,AB=FG.
所以四边形ABGF为平行四边形.所以AF//BG.
因为在正方体中,点E,G分别是棱的中点,
所以.
所以四边形为平行四边形.所以.
所以.
故点在平面AEF内.
···································14分
(19)(共14分)
解:(Ⅰ)由已知条件可得,又因为每组的小矩形的面职之和为1.
所以(0.035+0.025+0.02+0.004+8t)×10=1,解得t=0.002···································4分
(Ⅱ)由(Ⅰ)知:t=0.002,
所以调查评分在[40,50)中的人数是调查评分在[50,60)中人数的,
若按分层抽样抽取3人,则调查评分在[40,50)中有1人,在[50,60)中有2人,
设事件M=“在抽取的3人中,经心理疏导后至少有一人的心理等级转为B”.
因为经心理疏导后的等级转化情况相互独立,
所以
所以
故经心理疏导后至少有一人的心理等级转为B的概率为···································10分
(Ⅲ)由频率分布直方图可得,
45×0.02+55×0.04+65×0.14+75×0.2+85×0.35+95×0.25=80.7.
估计市民心理健康调查评分的平均值为80.7,
所以市民心理健康指数平均值为.
所以只需发放心理指导材料,不需要举办心理健康大讲堂活动.
···································14分
(20)(共14分)
解:选条件__①__,__③__
(Ⅰ)因为
又因为在中,,
所以···································4分
(II)因为△ABC是锐角三角形,由(Ⅰ)知
所以
在△ABC中,因为,
所以即,解得AC=5.
又因为EC=3,所以AE=2.
又因为DE=2,所以.故···································10分
(Ⅲ)因为,由(Ⅱ)知AC=5,
所以
又因为
所以
所以四边形BCED的面积为···································14分
选条件__②__,__③__.
(Ⅰ)因为
所以
所以
···································4分
(Ⅱ)由(Ⅰ)及正弦定理:得
又因为EC=3,所以AE=2,
又因为DE=2,所以故···································10分
(Ⅲ)因为△ABC是锐角三角形,由(Ⅰ)知
所以
由余弦定理得:
解得:.
所以
又因为
所以
所以四边形BCED的面积为···································14分
(21)(共14分)
解:(Ⅰ)为T点列.理由如下:
由题意可知,
所以
即f(n+1)>f(n),n=1,2,….
所以为T点列.
···································4分
(Ⅱ)由题意可知,
所以
因为为T点列,
所以
又因为,所以.
所以对中连续三点,都有
又
所以所以为.的最大内角
由余弦定理得:
故为钝角,所以为钝角三角形.
···································10分
(Ⅲ)由k
所以
······
两边分别相加可得
所以,
所以
所以
又
所以,
所以···································14分
7
/
12
同课章节目录
