青岛版六年级上册数学-第五单元 圆 单元培优测试卷(含答案)
文档属性
| 名称 | 青岛版六年级上册数学-第五单元 圆 单元培优测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 286.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-04 00:00:00 | ||
图片预览



文档简介
单元培优测试卷
第五单元 圆
一、填空。(每空1分,共20分)
1.战国时期墨家所著的《墨经》一书中记载:“圆,一中同长也。”表示圆上任意一点到( )的距离都相等,也就是圆的( )都相等。
2.一个圆的面积是28.26cm2 ,用圆规画圆时,圆规两脚之间的距离是( )cm。这个圆的直径是( )cm,周长是( )cm。
36175952952753.“外圆内方”与“外方内圆”是我国古代建筑中常见的设计,其中也蕴含了为人处世的朴素道理。如果下图中外面正方形的边长是6m,则内圆的面积是( )m2。
44615107048504.2020年6月21日,在我国境内观测到天文奇观日环食。乐乐把自己看到的日环食画下来(如图),把它近似看成一个圆环。内、外圆的直径分别是10cm、12cm,图中圆环的面积是( )cm2。
5.汝瓷位居我国宋代“五大名瓷”之首,被世人称为“似玉非玉而胜玉”。小亮用细绳绕一件汝瓷的圆形瓶口一周,量出长度是12.56 cm,这件汝瓷瓶口的直径是( )cm,瓶口的面积是( )cm2。
6.王叔叔家修建了一个半圆形的水池,并在水池的弧形部分外圈围了一条彩灯带,总长是9.42m,这个半圆形的水池的面积是( )m2。
34124902736857.如图,AB长20cm,一只蚂蚁从A到B沿着两个半圆形的弧爬行,蚂蚁爬行了( )cm。
8.在推导圆的面积公式过程中,我们运用了( )的方法。把一个圆形纸片分成若干等份,然后把它剪开,照下面的样子拼成一个近似的长方形。
(1)拼成长方形的宽等于圆的( ),长近似于圆( )。
(2)如果圆的半径是8cm,则这个长方形的长是( )cm,面积是( )cm2。
(3)如果圆的周长比长方形的周长少10cm,那么圆的半径是( )cm,面积是( )cm2。
38671501860559.如右图,在长方形内有甲、乙、丙三个圆,已知乙、丙两个圆相同,那么甲、乙两个圆的周长比是( ),面积比是( )。
二、判断。(对的在括号里打“√”,错的打“×”)(每题2分,共10分)
1.同一个圆的周长和半径的比是2π∶1。 ( )
2.如果圆的半径扩大到原来的4倍,那么圆的面积也扩大到原来的4倍。 ( )
3.直径是半径的2倍。 ( )
4.圆的周长是6.28 dm,那么半圆形的周长就是3.14 dm。( )
5.两个圆比较,周长较小的那个圆面积也一定小。 ( )
三、选择。(将正确答案的字母填在括号里)(每题2分,共10分)
1.把一个圆至少对折( )次才能够找到圆心。
A.1 B.2 C.3 D.4
2.下面属于“黄金比”的是( )。
A.圆的周长∶直径≈3.14∶1
B.一条线段分成两部分,较短部分∶较长部分≈0.618∶1
C.八分音符∶全音符=1∶8
D.食品支出总额∶小康家庭消费支出总额=1∶2
422021011417303.下图是“禁止驶入”交通标志,标志中有一个尺寸是70cm×12cm的白色长方形,其余部分是红色。计算这个交通标志中红色部分的面积,下面列式正确的是( )。
A.×(80÷2)2π B.(80÷2)2π-70×12
C.×802π D.802π-70×12
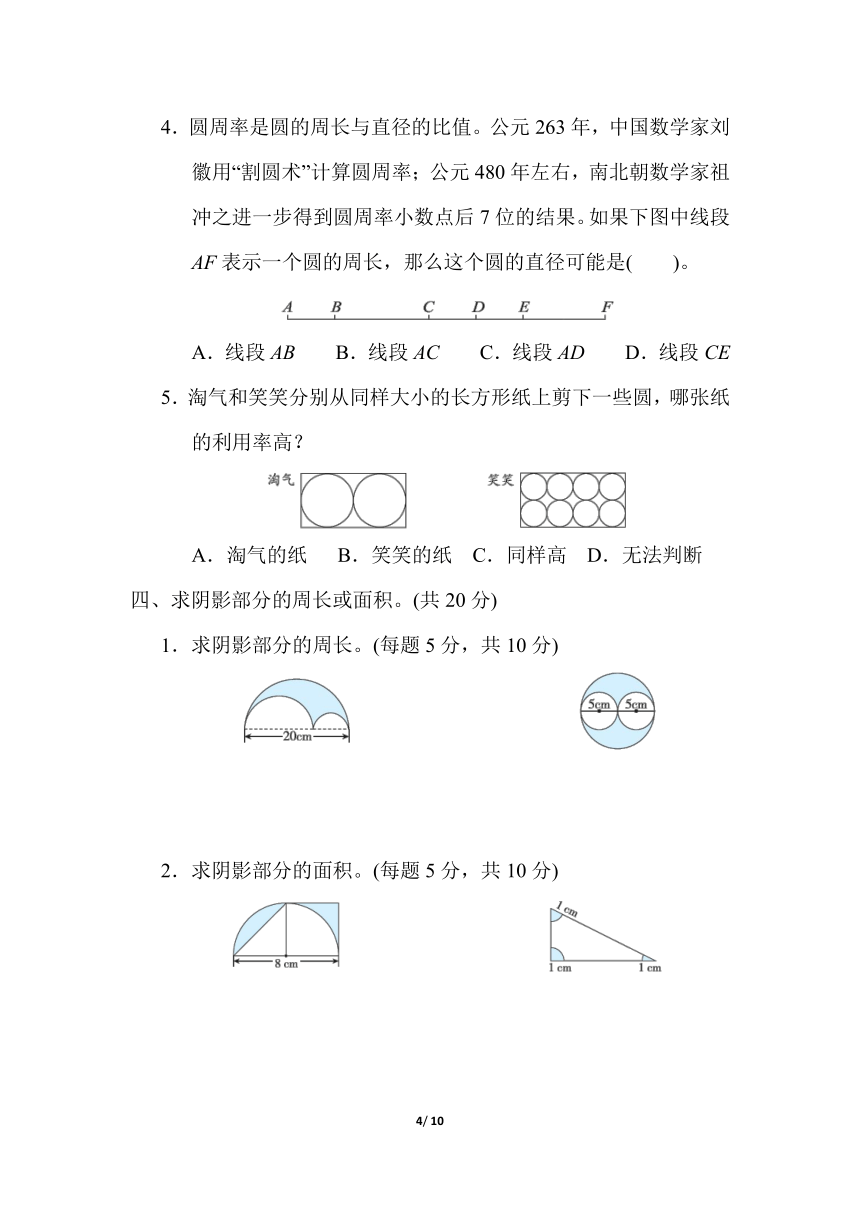
4.圆周率是圆的周长与直径的比值。公元263年,中国数学家刘徽用“割圆术”计算圆周率;公元480年左右,南北朝数学家祖冲之进一步得到圆周率小数点后7位的结果。如果下图中线段AF表示一个圆的周长,那么这个圆的直径可能是( )。
A.线段AB B.线段AC C.线段AD D.线段CE
5.淘气和笑笑分别从同样大小的长方形纸上剪下一些圆,哪张纸的利用率高?
A.淘气的纸 B.笑笑的纸 C.同样高 D.无法判断
四、求阴影部分的周长或面积。(共20分)
1.求阴影部分的周长。(每题5分,共10分)
2.求阴影部分的面积。(每题5分,共10分)
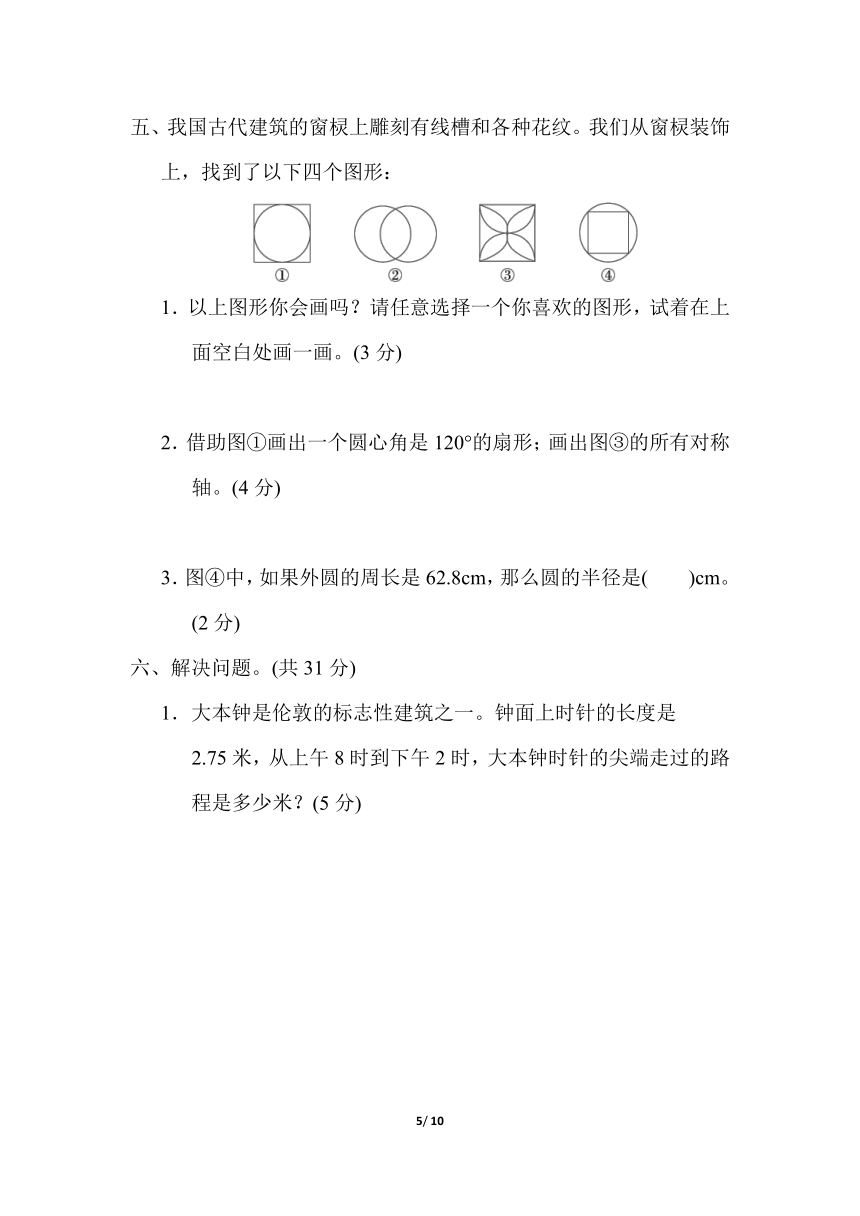
五、我国古代建筑的窗棂上雕刻有线槽和各种花纹。我们从窗棂装饰上,找到了以下四个图形:
1.以上图形你会画吗?请任意选择一个你喜欢的图形,试着在上面空白处画一画。(3分)
2.借助图①画出一个圆心角是120°的扇形;画出图③的所有对称轴。(4分)
3.图④中,如果外圆的周长是62.8cm,那么圆的半径是( )cm。(2分)
六、解决问题。(共31分)
1.大本钟是伦敦的标志性建筑之一。钟面上时针的长度是
2.75米,从上午8时到下午2时,大本钟时针的尖端走过的路程是多少米?(5分)
2.丽丽的爸爸是一个象棋爱好者,她家有一个刻有象棋盘的圆形石桌。爸爸经常和棋友在这里切磋棋艺。
(1)这个圆形石桌的直径是1.1米,它的周长是多少米?(5分)
(2)如果按照一个人至少需要0.8米宽的位置就座,这个石桌周围最多可以放多少个石凳?(5分)
3.一个环形建筑,内直径400米,环宽30米,这个环形建筑的面积是多少平方米?(5分)
4.在求一个直径为30米的圆形水池的周长时,哲哲忘记了圆周率的数值,但他记得求圆周率的方法。哲哲随机在纸上剪了一个直径1厘米的圆形纸片,将该圆形纸片在直尺上滚动5周,测得大约滚动了15.7厘米,于是求得了圆周率。请你写出哲哲求圆周率的计算过程并求出水池的周长。(5分)
5.商店的售货员将四瓶啤酒扎在一起,如下图所示,你知道至少要用多少厘米的绳子吗?(接头处忽略不计)(6分)
七、附加题:天才的你,试一试。(10分)
如图,有一只狗被拴在一建筑物的墙角点A处,建筑物的底面是一个边长为8m的正方形,拴狗的绳长18m。现在狗从点B沿顺时针方向跑。狗最多可以跑多少米?
答案
一、1.圆心 半径
2.3 6 18.84
3.28.26
4.34.54
5.4 12.56
6.14.13
7.31.4
8.化圆为方
(1)半径 周长的一半 (2)25.12 200.96
(3) 5 78.5
9.2∶1 4∶1
二、1.√ 2.×
3.× 4.× 5.√
三、1.B 2.B
3.B 4.D 5.C
四、1.3.14×20=62.8(cm)
3.14×(5+5)×2=62.8(cm)
2.(8÷2)×(8÷2)÷2=8(cm2)
3.14×12÷2=1.57(cm2)
五、1.(答案不唯一)
2.
3.10
六、1.3.14×2.75=8.635(米)
答:大本钟时针的尖端走过的路程是8.635米。
从上午8时到下午2时,经历的时间为12+2-8=6(小时),时针走过的是半径为2.75米的圆的周长的一半,即为πr=3.14×2.75=8.635(米)。
2.(1)3.14×1.1=3.454(米)
答:它的周长是3.454米。
(2)3.454÷0.8≈4(个)
答:这个石桌周围最多可以放4个石凳。
(1)根据圆周长=πd,即可求出圆形石桌的周长是3.14×1.1=3.454(米);(2)用石桌的周长除以一个人需要的位置宽度即可算出最多能放多少个石凳,列式为3.454÷0.8≈4(个)。
3.400÷2=200(米) 200+30=230(米)
3.14×(2302-2002)=40506(平方米)
答:这个环形建筑的面积是40506平方米。
4.15.7÷5÷1=3.14 3.14×30=94.2(米)
答:水池的周长为94.2米。
5.4×7+3.14×7=49.98(cm)
答:至少要用49.98cm的绳子。
七、附加题:
×2×3.14×18+×2×3.14×(18-8)+
×2×3.14×(18-8-8)=47.1(m)
答:狗最多可以跑47.1m。
狗沿顺时针方向跑的路径是半径为18m的圆周长的加上半径为(18-8)m的圆周长的,再加上半径为(18-8-8)m的圆周长的。
第五单元 圆
一、填空。(每空1分,共20分)
1.战国时期墨家所著的《墨经》一书中记载:“圆,一中同长也。”表示圆上任意一点到( )的距离都相等,也就是圆的( )都相等。
2.一个圆的面积是28.26cm2 ,用圆规画圆时,圆规两脚之间的距离是( )cm。这个圆的直径是( )cm,周长是( )cm。
36175952952753.“外圆内方”与“外方内圆”是我国古代建筑中常见的设计,其中也蕴含了为人处世的朴素道理。如果下图中外面正方形的边长是6m,则内圆的面积是( )m2。
44615107048504.2020年6月21日,在我国境内观测到天文奇观日环食。乐乐把自己看到的日环食画下来(如图),把它近似看成一个圆环。内、外圆的直径分别是10cm、12cm,图中圆环的面积是( )cm2。
5.汝瓷位居我国宋代“五大名瓷”之首,被世人称为“似玉非玉而胜玉”。小亮用细绳绕一件汝瓷的圆形瓶口一周,量出长度是12.56 cm,这件汝瓷瓶口的直径是( )cm,瓶口的面积是( )cm2。
6.王叔叔家修建了一个半圆形的水池,并在水池的弧形部分外圈围了一条彩灯带,总长是9.42m,这个半圆形的水池的面积是( )m2。
34124902736857.如图,AB长20cm,一只蚂蚁从A到B沿着两个半圆形的弧爬行,蚂蚁爬行了( )cm。
8.在推导圆的面积公式过程中,我们运用了( )的方法。把一个圆形纸片分成若干等份,然后把它剪开,照下面的样子拼成一个近似的长方形。
(1)拼成长方形的宽等于圆的( ),长近似于圆( )。
(2)如果圆的半径是8cm,则这个长方形的长是( )cm,面积是( )cm2。
(3)如果圆的周长比长方形的周长少10cm,那么圆的半径是( )cm,面积是( )cm2。
38671501860559.如右图,在长方形内有甲、乙、丙三个圆,已知乙、丙两个圆相同,那么甲、乙两个圆的周长比是( ),面积比是( )。
二、判断。(对的在括号里打“√”,错的打“×”)(每题2分,共10分)
1.同一个圆的周长和半径的比是2π∶1。 ( )
2.如果圆的半径扩大到原来的4倍,那么圆的面积也扩大到原来的4倍。 ( )
3.直径是半径的2倍。 ( )
4.圆的周长是6.28 dm,那么半圆形的周长就是3.14 dm。( )
5.两个圆比较,周长较小的那个圆面积也一定小。 ( )
三、选择。(将正确答案的字母填在括号里)(每题2分,共10分)
1.把一个圆至少对折( )次才能够找到圆心。
A.1 B.2 C.3 D.4
2.下面属于“黄金比”的是( )。
A.圆的周长∶直径≈3.14∶1
B.一条线段分成两部分,较短部分∶较长部分≈0.618∶1
C.八分音符∶全音符=1∶8
D.食品支出总额∶小康家庭消费支出总额=1∶2
422021011417303.下图是“禁止驶入”交通标志,标志中有一个尺寸是70cm×12cm的白色长方形,其余部分是红色。计算这个交通标志中红色部分的面积,下面列式正确的是( )。
A.×(80÷2)2π B.(80÷2)2π-70×12
C.×802π D.802π-70×12
4.圆周率是圆的周长与直径的比值。公元263年,中国数学家刘徽用“割圆术”计算圆周率;公元480年左右,南北朝数学家祖冲之进一步得到圆周率小数点后7位的结果。如果下图中线段AF表示一个圆的周长,那么这个圆的直径可能是( )。
A.线段AB B.线段AC C.线段AD D.线段CE
5.淘气和笑笑分别从同样大小的长方形纸上剪下一些圆,哪张纸的利用率高?
A.淘气的纸 B.笑笑的纸 C.同样高 D.无法判断
四、求阴影部分的周长或面积。(共20分)
1.求阴影部分的周长。(每题5分,共10分)
2.求阴影部分的面积。(每题5分,共10分)
五、我国古代建筑的窗棂上雕刻有线槽和各种花纹。我们从窗棂装饰上,找到了以下四个图形:
1.以上图形你会画吗?请任意选择一个你喜欢的图形,试着在上面空白处画一画。(3分)
2.借助图①画出一个圆心角是120°的扇形;画出图③的所有对称轴。(4分)
3.图④中,如果外圆的周长是62.8cm,那么圆的半径是( )cm。(2分)
六、解决问题。(共31分)
1.大本钟是伦敦的标志性建筑之一。钟面上时针的长度是
2.75米,从上午8时到下午2时,大本钟时针的尖端走过的路程是多少米?(5分)
2.丽丽的爸爸是一个象棋爱好者,她家有一个刻有象棋盘的圆形石桌。爸爸经常和棋友在这里切磋棋艺。
(1)这个圆形石桌的直径是1.1米,它的周长是多少米?(5分)
(2)如果按照一个人至少需要0.8米宽的位置就座,这个石桌周围最多可以放多少个石凳?(5分)
3.一个环形建筑,内直径400米,环宽30米,这个环形建筑的面积是多少平方米?(5分)
4.在求一个直径为30米的圆形水池的周长时,哲哲忘记了圆周率的数值,但他记得求圆周率的方法。哲哲随机在纸上剪了一个直径1厘米的圆形纸片,将该圆形纸片在直尺上滚动5周,测得大约滚动了15.7厘米,于是求得了圆周率。请你写出哲哲求圆周率的计算过程并求出水池的周长。(5分)
5.商店的售货员将四瓶啤酒扎在一起,如下图所示,你知道至少要用多少厘米的绳子吗?(接头处忽略不计)(6分)
七、附加题:天才的你,试一试。(10分)
如图,有一只狗被拴在一建筑物的墙角点A处,建筑物的底面是一个边长为8m的正方形,拴狗的绳长18m。现在狗从点B沿顺时针方向跑。狗最多可以跑多少米?
答案
一、1.圆心 半径
2.3 6 18.84
3.28.26
4.34.54
5.4 12.56
6.14.13
7.31.4
8.化圆为方
(1)半径 周长的一半 (2)25.12 200.96
(3) 5 78.5
9.2∶1 4∶1
二、1.√ 2.×
3.× 4.× 5.√
三、1.B 2.B
3.B 4.D 5.C
四、1.3.14×20=62.8(cm)
3.14×(5+5)×2=62.8(cm)
2.(8÷2)×(8÷2)÷2=8(cm2)
3.14×12÷2=1.57(cm2)
五、1.(答案不唯一)
2.
3.10
六、1.3.14×2.75=8.635(米)
答:大本钟时针的尖端走过的路程是8.635米。
从上午8时到下午2时,经历的时间为12+2-8=6(小时),时针走过的是半径为2.75米的圆的周长的一半,即为πr=3.14×2.75=8.635(米)。
2.(1)3.14×1.1=3.454(米)
答:它的周长是3.454米。
(2)3.454÷0.8≈4(个)
答:这个石桌周围最多可以放4个石凳。
(1)根据圆周长=πd,即可求出圆形石桌的周长是3.14×1.1=3.454(米);(2)用石桌的周长除以一个人需要的位置宽度即可算出最多能放多少个石凳,列式为3.454÷0.8≈4(个)。
3.400÷2=200(米) 200+30=230(米)
3.14×(2302-2002)=40506(平方米)
答:这个环形建筑的面积是40506平方米。
4.15.7÷5÷1=3.14 3.14×30=94.2(米)
答:水池的周长为94.2米。
5.4×7+3.14×7=49.98(cm)
答:至少要用49.98cm的绳子。
七、附加题:
×2×3.14×18+×2×3.14×(18-8)+
×2×3.14×(18-8-8)=47.1(m)
答:狗最多可以跑47.1m。
狗沿顺时针方向跑的路径是半径为18m的圆周长的加上半径为(18-8)m的圆周长的,再加上半径为(18-8-8)m的圆周长的。
