2020-2021学年上海市浦东新区上南中学南校七年级(下)期末数学试卷(word版无答案)
文档属性
| 名称 | 2020-2021学年上海市浦东新区上南中学南校七年级(下)期末数学试卷(word版无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 22:42:08 | ||
图片预览

文档简介
2020-2021学年上海市浦东新区上南中学南校七年级(下)期末数学试卷
一、选择题(本大题共6题,每题2分,共12分)
1.下列实数中,一定是无理数的是( )
A. B.0.1010010001
C. D.3.14
2.下列计算正确的是( )
A. B.
C. D.
3.据报道,国新办于2021年5月11日上午就第七次全国人口普查主要数据结果举行发布会,发布会上透露全国人口已达14.1178亿人,这里的近似数“14.1178亿”精确到( )
A.亿位 B.千万位 C.万分位 D.万位
4.如图,能说明AB∥DE的条件有( )
①∠1=∠D
②∠CFB+∠D=180°
③∠B=∠D
④∠BFD=∠D
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的是( )
A.三角形的外角等于两个内角的和
B.等腰三角形的角平分线和中线重合
C.含60°的两个直角三角形全等
D.有一个角是60°的等腰三角形是等边三角形
6.点P的横坐标是﹣3,且到X轴的距离为5,则点P的坐标是( )
A.(5,﹣3)或(﹣5,﹣3) B.(﹣3,5)或(﹣3,﹣5)
C.(﹣3,5) D.(﹣3,﹣5)
二、填空题(本大题共12题,每题3分,共36分)
7.的平方根是 .
8.把表示成幂的形式为 .
9.比较大小:﹣4 (填“>”、“=”或“<”).
10.近似数1.024有 个有效数字.
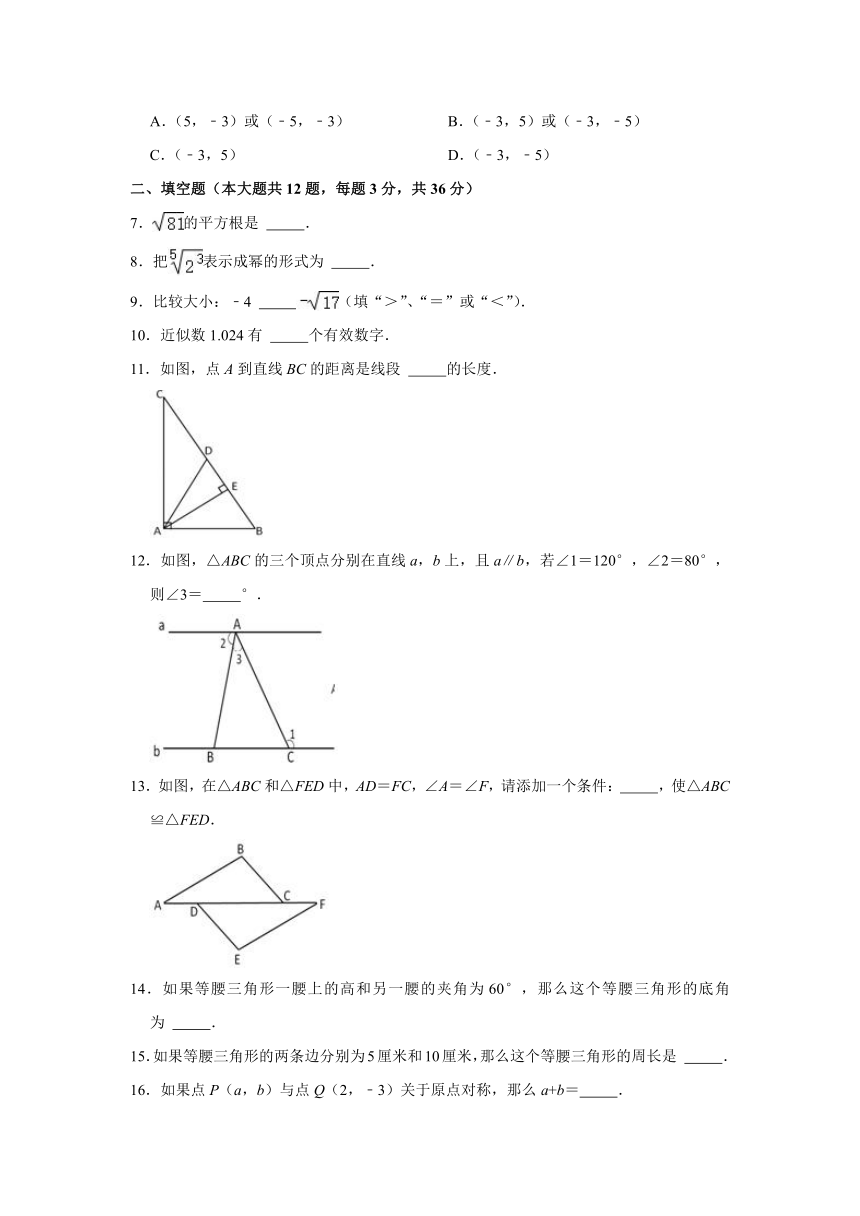
11.如图,点A到直线BC的距离是线段 的长度.
12.如图,△ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3= °.
13.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件: ,使△ABC≌△FED.
14.如果等腰三角形一腰上的高和另一腰的夹角为60°,那么这个等腰三角形的底角为 .
15.如果等腰三角形的两条边分别为5厘米和10厘米,那么这个等腰三角形的周长是 .
16.如果点P(a,b)与点Q(2,﹣3)关于原点对称,那么a+b= .
17.在平面直角坐标系中,线段AB=3,且AB∥x轴,如果点A的坐标为(﹣1,2),那么点B的坐标是 .
18.如图,已知长方形纸片ABCD,点E、F分别在边AD、BC上,将长方形纸片沿着直线EF折叠后,点D、C分别落在D1、C1的位置,如果∠AED1=30°,那么∠EFB= °
三、简答题(本大题共4题,其中第19、20题每题5分,第21、22题每题6分,共22分)
19.计算:
20.利用幂的性质计算:
21.如图,在△ABC中,点E是AD上的一点,EB=EC,∠ABE=∠ACE,请说明AD⊥BC.
解:因为EB=EC(已知),
所以∠EBC=∠ECB
又因为∠ABE=∠ACE(已知)
所以∠ABE+∠EBC=∠ACE+∠ECB
即∠ABC=∠ACB
所以AB=AC
在△ABE和△ACE中,
AB=AC
EB=EC
AE=AE(公共边)
所以△ABE≌△ACE
得∠BAD=∠CAD
所以AD⊥BC
22.如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1与△ABC关于原点O对称.
(1)写出点A1、B1、C1的坐标,并在图中画出
(2)求△A1B1C1的面积.
四、解答题(本大题共4题,其中第23、24题每题7分,第25、26题每题8分,共30分)
23.如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
24.如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
25.如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.
(1)请说明△BCE≌△ACD;
(2)请说明CF=CH;
(3)判断△CFH的形状并说明理由.
26.在平面直角坐标系中,已知点A(﹣3,0),B(﹣2,﹣2),将线段AB平移到线段DC.
(1)如图1,直接写出线段AB和线段CD的位置和数量关系;
(2)如图2,若线段AB平移到线段DC,D、C两点恰好分别在y轴、x轴上,求点D和点C的坐标;
(3)若点D在y轴的正半轴上,点C在第一象限内,且S△ACD=5,直接写出点C、点D的坐标.
一、选择题(本大题共6题,每题2分,共12分)
1.下列实数中,一定是无理数的是( )
A. B.0.1010010001
C. D.3.14
2.下列计算正确的是( )
A. B.
C. D.
3.据报道,国新办于2021年5月11日上午就第七次全国人口普查主要数据结果举行发布会,发布会上透露全国人口已达14.1178亿人,这里的近似数“14.1178亿”精确到( )
A.亿位 B.千万位 C.万分位 D.万位
4.如图,能说明AB∥DE的条件有( )
①∠1=∠D
②∠CFB+∠D=180°
③∠B=∠D
④∠BFD=∠D
A.1个 B.2个 C.3个 D.4个
5.下列说法正确的是( )
A.三角形的外角等于两个内角的和
B.等腰三角形的角平分线和中线重合
C.含60°的两个直角三角形全等
D.有一个角是60°的等腰三角形是等边三角形
6.点P的横坐标是﹣3,且到X轴的距离为5,则点P的坐标是( )
A.(5,﹣3)或(﹣5,﹣3) B.(﹣3,5)或(﹣3,﹣5)
C.(﹣3,5) D.(﹣3,﹣5)
二、填空题(本大题共12题,每题3分,共36分)
7.的平方根是 .
8.把表示成幂的形式为 .
9.比较大小:﹣4 (填“>”、“=”或“<”).
10.近似数1.024有 个有效数字.
11.如图,点A到直线BC的距离是线段 的长度.
12.如图,△ABC的三个顶点分别在直线a,b上,且a∥b,若∠1=120°,∠2=80°,则∠3= °.
13.如图,在△ABC和△FED中,AD=FC,∠A=∠F,请添加一个条件: ,使△ABC≌△FED.
14.如果等腰三角形一腰上的高和另一腰的夹角为60°,那么这个等腰三角形的底角为 .
15.如果等腰三角形的两条边分别为5厘米和10厘米,那么这个等腰三角形的周长是 .
16.如果点P(a,b)与点Q(2,﹣3)关于原点对称,那么a+b= .
17.在平面直角坐标系中,线段AB=3,且AB∥x轴,如果点A的坐标为(﹣1,2),那么点B的坐标是 .
18.如图,已知长方形纸片ABCD,点E、F分别在边AD、BC上,将长方形纸片沿着直线EF折叠后,点D、C分别落在D1、C1的位置,如果∠AED1=30°,那么∠EFB= °
三、简答题(本大题共4题,其中第19、20题每题5分,第21、22题每题6分,共22分)
19.计算:
20.利用幂的性质计算:
21.如图,在△ABC中,点E是AD上的一点,EB=EC,∠ABE=∠ACE,请说明AD⊥BC.
解:因为EB=EC(已知),
所以∠EBC=∠ECB
又因为∠ABE=∠ACE(已知)
所以∠ABE+∠EBC=∠ACE+∠ECB
即∠ABC=∠ACB
所以AB=AC
在△ABE和△ACE中,
AB=AC
EB=EC
AE=AE(公共边)
所以△ABE≌△ACE
得∠BAD=∠CAD
所以AD⊥BC
22.如图,在平面直角坐标系中,O为坐标原点,△ABC的三个顶点坐标分别为A(﹣1,﹣2),B(1,1),C(﹣3,1),△A1B1C1与△ABC关于原点O对称.
(1)写出点A1、B1、C1的坐标,并在图中画出
(2)求△A1B1C1的面积.
四、解答题(本大题共4题,其中第23、24题每题7分,第25、26题每题8分,共30分)
23.如图,∠ABE=80°,BF是∠ABE的平分线,且BF∥CD,求∠C的度数.
24.如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
25.如图,已知点B,C,D在同一条直线上,△ABC和△CDE都是等边三角形,BE交AC于点F,AD交CE于点H.
(1)请说明△BCE≌△ACD;
(2)请说明CF=CH;
(3)判断△CFH的形状并说明理由.
26.在平面直角坐标系中,已知点A(﹣3,0),B(﹣2,﹣2),将线段AB平移到线段DC.
(1)如图1,直接写出线段AB和线段CD的位置和数量关系;
(2)如图2,若线段AB平移到线段DC,D、C两点恰好分别在y轴、x轴上,求点D和点C的坐标;
(3)若点D在y轴的正半轴上,点C在第一象限内,且S△ACD=5,直接写出点C、点D的坐标.
同课章节目录
