湖南省怀化市洪江市2020-2021学年人教版八年级数学下学期期末数学试卷(word版含答案)
文档属性
| 名称 | 湖南省怀化市洪江市2020-2021学年人教版八年级数学下学期期末数学试卷(word版含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 801.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-03 22:57:35 | ||
图片预览

文档简介
(
………………○………………外………………○………………装………………○………………订………………○………………
线
………………○………………
)
(
………………○………………内………………○………………装………………○………………订………………○………………
线
………………○………………
)
(
此卷只装订
不密封
)
(
………………○………………
内
………………○………………装………………○………………订………………○………………
线
………………○………………
………………○………………外………………○………………装………………○………………订………………○………………
线
………………○………………
…
学校:
______________
姓名:
_____________
班级:
_______________
考号:
______________________
)
绝密★启用前|
洪江市2021年上学期八年级期末数学试卷
(本试卷共6页,全卷满分
150
分,考试时长
120
分钟)
一、选择题(每小题4分,共40分)
1、下面的图形中,既是轴对称又是中心对称图形的是(
)
2.下列各组数据中,不能作为直角三角形边长的是(
)
A.3,5,7
B.6,8,10
C.5,12,13
D.1,2,
3,如图,在Rt△ABC中,∠ACB=90”,∠A=30”,CD
是斜边
AB上的高,BD=2,那么AD的长为(
)
4,小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过15min
的频率为(
)
A.0.1
B.0.4
C.0.5
D.0.9
第5题图
第7题图
第9题图
5.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AC=1.2km,BC=1.6km,则
M,C两点间的距离为(
)
A.2.0km
B.1.2km
C.1.0km
D.0.5km
6.对于函数y=1,下列结论正确的是(
)
A.它的图象必经过点(-1,3)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
7.如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
8.下列说法正确的是(
)
A.一组对边相等且有一个角是直角的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线相等且互相垂直的四边形是正方形
D.对角线平分一组对角的平行四边形是菱形
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC
折叠,则重叠部分△AFC的面积为(
)
10.在一次函数y=
中,y随x的增大而减小,则其图象可能是(
)
二、填空题(6小题,每小题4分,共24分)
11.若n边形的每一个外角都为
45°,则n的值为____________.
12.已知点P(3,a)关于y轴的对称点为Q(b,2),则ab=___________.
如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=4m,则A、B两点间的距离是____________m.
14.一个容量为80的样本,最大值为143,最小值为50,取组距为10.则可以分成_________组
15.已知m是整数,且一次函数y=(m+4)x+m+2的图象不过第二象限,则m=___________
如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A10,
如此下去,则线段OAn的长度为_________________
第13题图
第16题图
三、解答题(8小题,共86分)
17.(本题满分8分)
如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
18.(本题满分8分)
画出△ABC关于y轴
对称的
图形△A1B1C1.
(1)求△A1B1C1三个顶点的坐标.
(2)求△A1B1C1的面积
19.(本题满分10分)
为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且5020.(本题满分10分)
一架梯子长25
米,斜靠在一面墙上,梯子底端离墙7米:
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的项端下滑了4米到A’,那么梯子的底端在水平方向滑动了几米?
21.(本题满分12分)
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形:
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
22.(本题满分12分)
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途经C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地。甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是_______千米/时,t=________小时
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围:
(3)直接写出乙车出发多长时间两车相距
120
千米.
23.(本题满分14分)
如图,已知正方形ABCD的边长为,连接AC、BD交于点O,CE平分∠ACD交BD于点E.
(1)求
DE
的长:
(2)过点E作
EF⊥CE.
交AB
于点F,求BF的长
(3)过点E作
EG⊥CE.交CD于点G,求
DG的长
24.(本题满分14分)
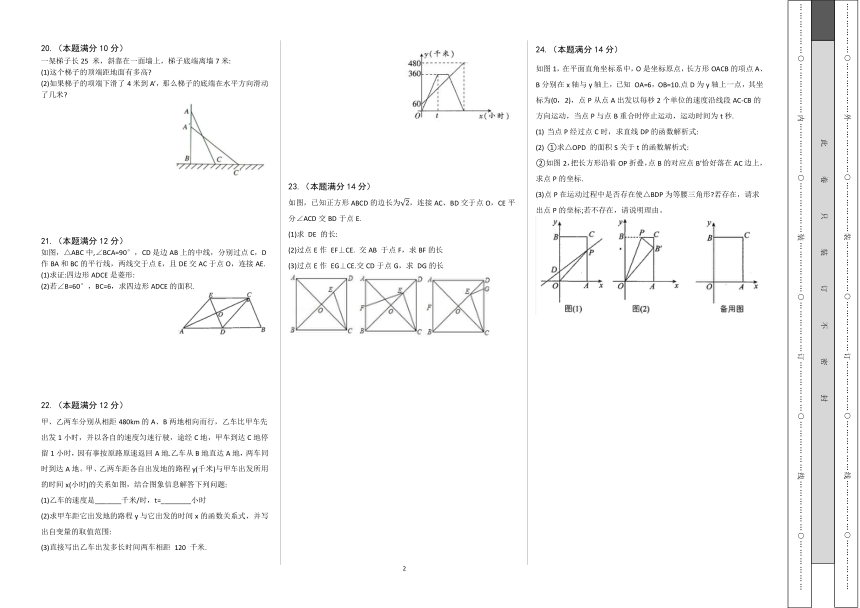
如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的项点A、B分别在x轴与y轴上,已知
OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC-CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
当点P经过点C时,求直线DP的函数解析式:
①求△OPD
的面积S关于t的函数解析式:
②如图2,把长方形沿着OP折叠,点B的对应点B’恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
八年级参考答案与试题解析
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】B
11.故答案为:8.
12.故答案为:﹣6.
13.故答案为:8.
14.故答案为:10.
15.故填空答案:﹣3
或﹣2.
16.故答案为:(
)n.
17.【解答】(本题酌情给分)
证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
∴△ABC
与△ACD
为直角三角形,
在
Rt△ABC
和
Rt△ADC
中,
∵AB=AD,AC
为公共边,
∴Rt△ABC≌Rt△ADC(HL),
∴∠1=∠2.
18.【解答】(画图
2
分,求坐标
3
分,求面积
3
分)
解:(1)如图所示:△A1B1C1
三个顶点的坐标:A1(-3,4),B1(-1,2),C1(-5,1);
(2)△A1B1C1
的面积为:3×4﹣
×2×3﹣
×2×2﹣
×1×4=5.
19.【解答】(本题每个小问题
2
分)
解:(1)由表格可得,
本次决赛的学生数为:10÷0.2=50,
故答案为:50;
(2)a=50×0.32=16,b=14÷50=0.28,
故答案为:16,0.28;
(3)补全的频数分布直方图如图所示,
(4)由表格可得,
决赛成绩不低于
80
分为优秀率为:(0.32+0.16)×100%=48%,
故答案为:48%.
20.【解答】(每问
5
分)解:(1)由题意得:AC=25
米,BC=7
米,
AB=
=24(米),
答:这个梯子的顶端距地面有
24
米;
(2)由题意得:BA′=20
米,
BC′==15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了
8
米.
21.【解答】(每问
6
分)(1)证明:∵DE∥BC,EC∥AB,
∴四边形
DBCE
是平行四边形.
∴EC∥DB,且
EC=DB.
在
Rt△ABC
中,CD
为
AB
边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形
ADCE
是平行四边形.
∴ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.
∴平行四边形
ADCE
是菱形;
(2)解:Rt△ABC
中,CD
为
AB
边上的中线,∠B=60°,BC=6,
∴AD=DB=CD=6.
∴AB=12,由勾股定理得
AC=
∵四边形
DBCE
是平行四边形,
∴DE=BC=6.
∴
S菱形ADCE=
22.【解答】解:(1)(共
4
分)根据图示,可得乙车的速度是
60
千米/时,
甲车的速度是:
(360×2)÷(480÷60﹣1﹣1)
=720÷6
=120(千米/小时)
∴t=360÷120=3(小时).
故答案为:60;3.
(2)(5
分)①当
0≤x≤3
时,设
y=k1x,
把(3,360)代入,可得
3k1=360,
解得
k1=120,
∴y=120x(0≤x≤3).
②当
3<x≤4
时,y=360.
③4<x≤7
时,设
y=k2x+b,
把(4,360)和(7,0)代入,可得
解得
∴y=﹣120x+840(4<x≤7).
综上所述:甲车距它出发地的路程
y
与它出发的时间
x
的函数关系式为
y=
(3)(3
分)①(480﹣60﹣120)÷(120+60)+1
=300÷180+1
=
+1
=
(小时)
②当甲车停留在
C
地时,
(480﹣360+120)÷60
=240÷60
=4(小时)
③两车都朝
A
地行驶时,
设乙车出发
m
小时后两车相距
120
千米,
则
60x﹣[120(m﹣1)﹣360]=120,
所以
480﹣60m=120,
所以
60m=360,
解得
m=6.
综上,可得
乙车出发
小时、4小时、6小时后两车相距120千米
23.【解答】(每问
4
分)解:(1)∵四边形
ABCD
是正方形,
∴∠ABC=∠ADC=90°,
∠DBC=∠BCA=∠ACD=45°,
∵CE
平分∠DCA,
∴∠ACE=∠DCE=
∠ACD=22.5°,
∴∠BCE=∠BCA+∠ACE=45°+22.5°=67.5°,
∵∠DBC=45°,
∴∠BEC=180°﹣67.5°﹣45°=67.5°=∠BCE,
∴BE=BC=
在
Rt△BCD
中,由勾股定理得:BD=
∴DE=BD﹣BE=2﹣
∵FE⊥CE,
∴∠CEF=90°,
∴∠FEB=∠CEF﹣∠CEB=90°﹣67.5°=22.5°=∠DCE,
∵∠FBE=∠CDE=45°,BE=BC=CD,
∴△FEB≌△ECD,
∴BF=DE=2﹣
过点
E
作
EN⊥CD
交
CD
于
N,
由(1)知:DE=2﹣
在等腰
Rt▲EDN
三角形中,用勾股定理可以求得:
∴EN=DN=
?
1,则
CN=1,在
Rt▲ECN
中用勾股定理可以求得:
CE2=CN2+EN2
设
DG=x;则
NG=
﹣1
﹣x
,CG=
?
x
;
在
Rt▲ENG
中,有
EG2=EN2+NG2……①
在
Rt▲ECG
中,有
EG2=CG2-CE2……②
解得:DG=3
﹣4.
24.【解答】解:(1)(3
分)∵OA=6,OB=10,四边形
OACB
为长方形,
∴C(6,10).
设此时直线
DP
解析式为
y=kx+b,
把(0,2),C(6,10)分别代入,得
解得
则此时直线
DP
解析式为
y=
x+2;
(2)①(4
分)当点
P
在线段
AC
上时,OD=2,高为
6,S=6;
当点
P
在线段
BC
上时,OD=2,高为
6+10﹣2t=16﹣2t,
S=
×2×(16﹣2t)=﹣2t+16;
②(4
分)设
P(m,10),则
PB=PB′=m,如图
2,
∵OB′=OB=10,OA=6,
∴AB′=
∴B′C=10﹣8=2,
∵PC=6﹣m,
∴m2=22+(6﹣m)2,解得
m=
则此时点
P
的坐标是(
,10);
(3)(3
分)存在,理由为:
因为
BD>BC,所以满足条件的点
P
在
AC
上.
若△BDP
为等腰三角形,分三种情况考虑:如图
3,
①当
BD=BP1=OB﹣OD=10﹣2=8,
在
Rt△BCP1
中,BP1=8,BC=6,
根据勾股定理得:CP1=
∴AP1=10﹣
,即
P1(6,10﹣
);
②当
BP2=DP2
时,此时
P2(6,6);
③当
DB=DP3=8
时,
在
Rt△DEP3
中,DE=6,
根据勾股定理得:P3E=
∴AP3=AE+EP3=
+
2
,即
P3(6,
+
2
),
综上,满足题意的
P
坐标为(6,6)或(6,
+
2)或(6,10)
………………○………………外………………○………………装………………○………………订………………○………………
线
………………○………………
)
(
………………○………………内………………○………………装………………○………………订………………○………………
线
………………○………………
)
(
此卷只装订
不密封
)
(
………………○………………
内
………………○………………装………………○………………订………………○………………
线
………………○………………
………………○………………外………………○………………装………………○………………订………………○………………
线
………………○………………
…
学校:
______________
姓名:
_____________
班级:
_______________
考号:
______________________
)
绝密★启用前|
洪江市2021年上学期八年级期末数学试卷
(本试卷共6页,全卷满分
150
分,考试时长
120
分钟)
一、选择题(每小题4分,共40分)
1、下面的图形中,既是轴对称又是中心对称图形的是(
)
2.下列各组数据中,不能作为直角三角形边长的是(
)
A.3,5,7
B.6,8,10
C.5,12,13
D.1,2,
3,如图,在Rt△ABC中,∠ACB=90”,∠A=30”,CD
是斜边
AB上的高,BD=2,那么AD的长为(
)
4,小明统计了他家今年5月份打电话的次数及通话时间,并列出了频数分布表:
则通话时间不超过15min
的频率为(
)
A.0.1
B.0.4
C.0.5
D.0.9
第5题图
第7题图
第9题图
5.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AC=1.2km,BC=1.6km,则
M,C两点间的距离为(
)
A.2.0km
B.1.2km
C.1.0km
D.0.5km
6.对于函数y=1,下列结论正确的是(
)
A.它的图象必经过点(-1,3)
B.它的图象经过第一、二、三象限
C.当x>1时,y<0
D.y的值随x值的增大而增大
7.如图,在△ABC中,∠B=90°,AD平分∠BAC,BC=10,CD=6,则点D到AC的距离为(
)
A.4
B.6
C.8
D.10
8.下列说法正确的是(
)
A.一组对边相等且有一个角是直角的四边形是矩形
B.对角线互相垂直的四边形是菱形
C.对角线相等且互相垂直的四边形是正方形
D.对角线平分一组对角的平行四边形是菱形
如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC
折叠,则重叠部分△AFC的面积为(
)
10.在一次函数y=
中,y随x的增大而减小,则其图象可能是(
)
二、填空题(6小题,每小题4分,共24分)
11.若n边形的每一个外角都为
45°,则n的值为____________.
12.已知点P(3,a)关于y轴的对称点为Q(b,2),则ab=___________.
如图,为估计池塘岸边A、B两点间的距离,在池塘的一侧选取点O,分别取OA、OB的中点M、N,测得MN=4m,则A、B两点间的距离是____________m.
14.一个容量为80的样本,最大值为143,最小值为50,取组距为10.则可以分成_________组
15.已知m是整数,且一次函数y=(m+4)x+m+2的图象不过第二象限,则m=___________
如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A10,
如此下去,则线段OAn的长度为_________________
第13题图
第16题图
三、解答题(8小题,共86分)
17.(本题满分8分)
如图,AB⊥BC,AD⊥DC,AB=AD,求证:∠1=∠2.
18.(本题满分8分)
画出△ABC关于y轴
对称的
图形△A1B1C1.
(1)求△A1B1C1三个顶点的坐标.
(2)求△A1B1C1的面积
19.(本题满分10分)
为了提高学生书写汉字的能力,增强保护汉字的意识,某校举办了首届“汉字听写大赛”,学生经选拔后进入决赛,测试同时听写100个汉字,每正确听写出一个汉字得1分,本次决赛,学生成绩为x(分),且50
一架梯子长25
米,斜靠在一面墙上,梯子底端离墙7米:
(1)这个梯子的顶端距地面有多高?
(2)如果梯子的项端下滑了4米到A’,那么梯子的底端在水平方向滑动了几米?
21.(本题满分12分)
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA和BC的平行线,两线交于点E,且DE交AC于点O,连接AE.
(1)求证:四边形ADCE是菱形:
(2)若∠B=60°,BC=6,求四边形ADCE的面积.
22.(本题满分12分)
甲、乙两车分别从相距480km的A、B两地相向而行,乙车比甲车先出发1小时,并以各自的速度匀速行驶,途经C地,甲车到达C地停留1小时,因有事按原路原速返回A地.乙车从B地直达A地,两车同时到达A地。甲、乙两车距各自出发地的路程y(千米)与甲车出发所用的时间x(小时)的关系如图,结合图象信息解答下列问题:
(1)乙车的速度是_______千米/时,t=________小时
(2)求甲车距它出发地的路程y与它出发的时间x的函数关系式,并写出自变量的取值范围:
(3)直接写出乙车出发多长时间两车相距
120
千米.
23.(本题满分14分)
如图,已知正方形ABCD的边长为,连接AC、BD交于点O,CE平分∠ACD交BD于点E.
(1)求
DE
的长:
(2)过点E作
EF⊥CE.
交AB
于点F,求BF的长
(3)过点E作
EG⊥CE.交CD于点G,求
DG的长
24.(本题满分14分)
如图1,在平面直角坐标系中,O是坐标原点,长方形OACB的项点A、B分别在x轴与y轴上,已知
OA=6,OB=10.点D为y轴上一点,其坐标为(0,2),点P从点A出发以每秒2个单位的速度沿线段AC-CB的方向运动,当点P与点B重合时停止运动,运动时间为t秒.
当点P经过点C时,求直线DP的函数解析式:
①求△OPD
的面积S关于t的函数解析式:
②如图2,把长方形沿着OP折叠,点B的对应点B’恰好落在AC边上,求点P的坐标.
(3)点P在运动过程中是否存在使△BDP为等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由。
八年级参考答案与试题解析
1.【答案】C
2.【答案】A
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】A
8.【答案】D
9.【答案】B
10.【答案】B
11.故答案为:8.
12.故答案为:﹣6.
13.故答案为:8.
14.故答案为:10.
15.故填空答案:﹣3
或﹣2.
16.故答案为:(
)n.
17.【解答】(本题酌情给分)
证明:∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°,
∴△ABC
与△ACD
为直角三角形,
在
Rt△ABC
和
Rt△ADC
中,
∵AB=AD,AC
为公共边,
∴Rt△ABC≌Rt△ADC(HL),
∴∠1=∠2.
18.【解答】(画图
2
分,求坐标
3
分,求面积
3
分)
解:(1)如图所示:△A1B1C1
三个顶点的坐标:A1(-3,4),B1(-1,2),C1(-5,1);
(2)△A1B1C1
的面积为:3×4﹣
×2×3﹣
×2×2﹣
×1×4=5.
19.【解答】(本题每个小问题
2
分)
解:(1)由表格可得,
本次决赛的学生数为:10÷0.2=50,
故答案为:50;
(2)a=50×0.32=16,b=14÷50=0.28,
故答案为:16,0.28;
(3)补全的频数分布直方图如图所示,
(4)由表格可得,
决赛成绩不低于
80
分为优秀率为:(0.32+0.16)×100%=48%,
故答案为:48%.
20.【解答】(每问
5
分)解:(1)由题意得:AC=25
米,BC=7
米,
AB=
=24(米),
答:这个梯子的顶端距地面有
24
米;
(2)由题意得:BA′=20
米,
BC′==15(米),
则:CC′=15﹣7=8(米),
答:梯子的底端在水平方向滑动了
8
米.
21.【解答】(每问
6
分)(1)证明:∵DE∥BC,EC∥AB,
∴四边形
DBCE
是平行四边形.
∴EC∥DB,且
EC=DB.
在
Rt△ABC
中,CD
为
AB
边上的中线,
∴AD=DB=CD.
∴EC=AD.
∴四边形
ADCE
是平行四边形.
∴ED∥BC.
∴∠AOD=∠ACB.
∵∠ACB=90°,
∴∠AOD=∠ACB=90°.
∴平行四边形
ADCE
是菱形;
(2)解:Rt△ABC
中,CD
为
AB
边上的中线,∠B=60°,BC=6,
∴AD=DB=CD=6.
∴AB=12,由勾股定理得
AC=
∵四边形
DBCE
是平行四边形,
∴DE=BC=6.
∴
S菱形ADCE=
22.【解答】解:(1)(共
4
分)根据图示,可得乙车的速度是
60
千米/时,
甲车的速度是:
(360×2)÷(480÷60﹣1﹣1)
=720÷6
=120(千米/小时)
∴t=360÷120=3(小时).
故答案为:60;3.
(2)(5
分)①当
0≤x≤3
时,设
y=k1x,
把(3,360)代入,可得
3k1=360,
解得
k1=120,
∴y=120x(0≤x≤3).
②当
3<x≤4
时,y=360.
③4<x≤7
时,设
y=k2x+b,
把(4,360)和(7,0)代入,可得
解得
∴y=﹣120x+840(4<x≤7).
综上所述:甲车距它出发地的路程
y
与它出发的时间
x
的函数关系式为
y=
(3)(3
分)①(480﹣60﹣120)÷(120+60)+1
=300÷180+1
=
+1
=
(小时)
②当甲车停留在
C
地时,
(480﹣360+120)÷60
=240÷60
=4(小时)
③两车都朝
A
地行驶时,
设乙车出发
m
小时后两车相距
120
千米,
则
60x﹣[120(m﹣1)﹣360]=120,
所以
480﹣60m=120,
所以
60m=360,
解得
m=6.
综上,可得
乙车出发
小时、4小时、6小时后两车相距120千米
23.【解答】(每问
4
分)解:(1)∵四边形
ABCD
是正方形,
∴∠ABC=∠ADC=90°,
∠DBC=∠BCA=∠ACD=45°,
∵CE
平分∠DCA,
∴∠ACE=∠DCE=
∠ACD=22.5°,
∴∠BCE=∠BCA+∠ACE=45°+22.5°=67.5°,
∵∠DBC=45°,
∴∠BEC=180°﹣67.5°﹣45°=67.5°=∠BCE,
∴BE=BC=
在
Rt△BCD
中,由勾股定理得:BD=
∴DE=BD﹣BE=2﹣
∵FE⊥CE,
∴∠CEF=90°,
∴∠FEB=∠CEF﹣∠CEB=90°﹣67.5°=22.5°=∠DCE,
∵∠FBE=∠CDE=45°,BE=BC=CD,
∴△FEB≌△ECD,
∴BF=DE=2﹣
过点
E
作
EN⊥CD
交
CD
于
N,
由(1)知:DE=2﹣
在等腰
Rt▲EDN
三角形中,用勾股定理可以求得:
∴EN=DN=
?
1,则
CN=1,在
Rt▲ECN
中用勾股定理可以求得:
CE2=CN2+EN2
设
DG=x;则
NG=
﹣1
﹣x
,CG=
?
x
;
在
Rt▲ENG
中,有
EG2=EN2+NG2……①
在
Rt▲ECG
中,有
EG2=CG2-CE2……②
解得:DG=3
﹣4.
24.【解答】解:(1)(3
分)∵OA=6,OB=10,四边形
OACB
为长方形,
∴C(6,10).
设此时直线
DP
解析式为
y=kx+b,
把(0,2),C(6,10)分别代入,得
解得
则此时直线
DP
解析式为
y=
x+2;
(2)①(4
分)当点
P
在线段
AC
上时,OD=2,高为
6,S=6;
当点
P
在线段
BC
上时,OD=2,高为
6+10﹣2t=16﹣2t,
S=
×2×(16﹣2t)=﹣2t+16;
②(4
分)设
P(m,10),则
PB=PB′=m,如图
2,
∵OB′=OB=10,OA=6,
∴AB′=
∴B′C=10﹣8=2,
∵PC=6﹣m,
∴m2=22+(6﹣m)2,解得
m=
则此时点
P
的坐标是(
,10);
(3)(3
分)存在,理由为:
因为
BD>BC,所以满足条件的点
P
在
AC
上.
若△BDP
为等腰三角形,分三种情况考虑:如图
3,
①当
BD=BP1=OB﹣OD=10﹣2=8,
在
Rt△BCP1
中,BP1=8,BC=6,
根据勾股定理得:CP1=
∴AP1=10﹣
,即
P1(6,10﹣
);
②当
BP2=DP2
时,此时
P2(6,6);
③当
DB=DP3=8
时,
在
Rt△DEP3
中,DE=6,
根据勾股定理得:P3E=
∴AP3=AE+EP3=
+
2
,即
P3(6,
+
2
),
综上,满足题意的
P
坐标为(6,6)或(6,
+
2)或(6,10)
同课章节目录
