第一章 反比例函数专项训练:反比例函数中的面积问题求解技巧(含答案)
文档属性
| 名称 | 第一章 反比例函数专项训练:反比例函数中的面积问题求解技巧(含答案) | 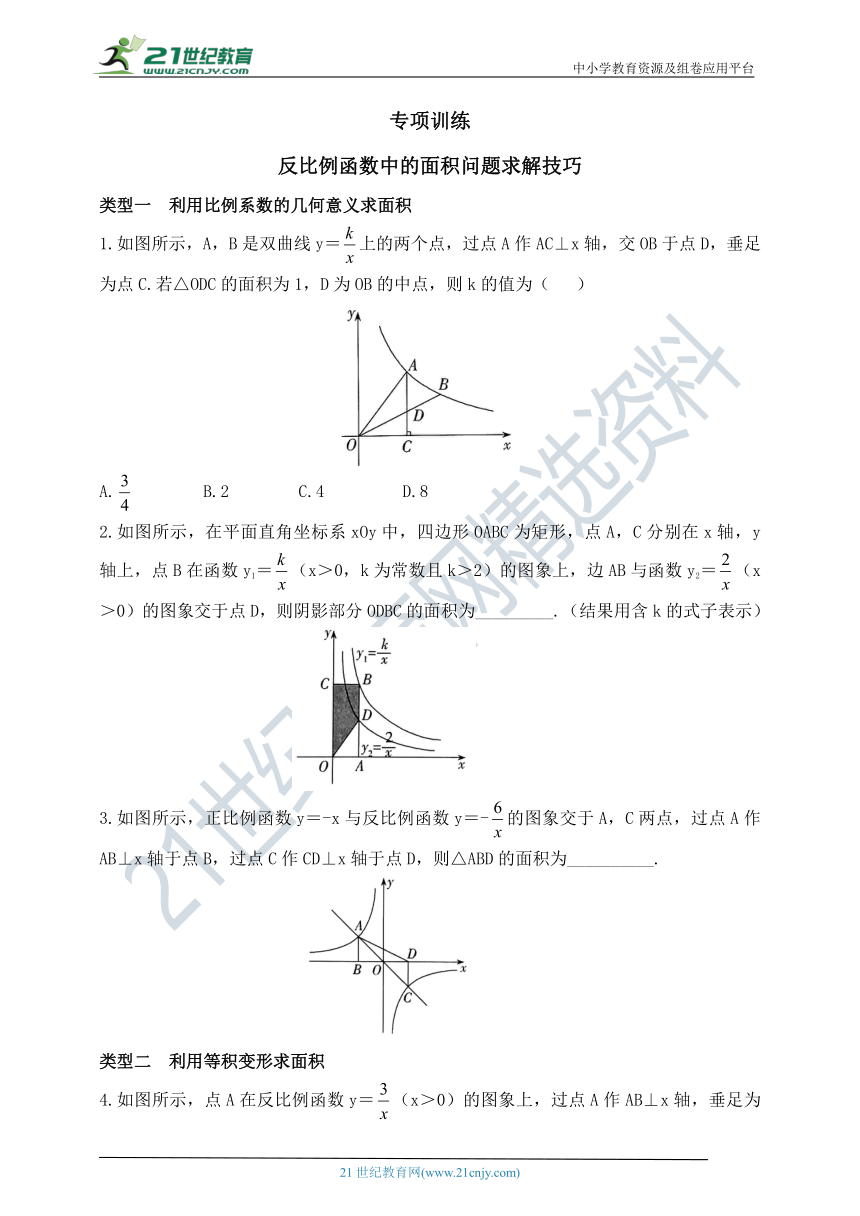 | |
| 格式 | doc | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 06:49:23 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专项训练
反比例函数中的面积问题求解技巧
类型一 利用比例系数的几何意义求面积
1.如图所示,A,B是双曲线y=上的两个点,过点A作AC⊥x轴,交OB于点D,垂足为点C.若△ODC的面积为1,D为OB的中点,则k的值为( )
A. B.2 C.4 D.8
2.如图所示,在平面直角坐标系xOy中,四边形OABC为矩形,点A,C分别在x轴,y轴上,点B在函数y1=(x>0,k为常数且k>2)的图象上,边AB与函数y2=(x>0)的图象交于点D,则阴影部分ODBC的面积为_________.(结果用含k的式子表示)
3.如图所示,正比例函数y=-x与反比例函数y=-的图象交于A,C两点,过点A作AB⊥x轴于点B,过点C作CD⊥x轴于点D,则△ABD的面积为__________.
类型二 利用等积变形求面积
4.如图所示,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A.3 B.2 C. D.1
5.如图所示,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的个动点.若△ABC的面积为4,则k1-k2的值为( )
A.8 B.-8 C.4 D.-4
类型三 利用和差法求面积
6.如图所示,点A在双曲线y=上,点B在双曲线y=上,且AB∥x轴,点C,D在x轴上,若四边形ABCD为矩形,则它的面积为( )
A.8 B.6 C.8 D.12
类型四 利用转化法求面积
7.如图所示,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD=,则k的值为( )
A.3 B. C.2 D.1
8.如图所示,平行四边形OABC的顶点C在反比例函数y=(k≠0)的图象上,点O为原点,A(-2,-1),B(1,-3),延长OB交反比例函数y=(k≠0)的图象于点D,连接CD.
(1)求反比例函数的表达式;
(2)求点D的坐标;
(3)试计算△OCD的面积.
类型五 利用割补法求面积
9.如图所示,点A是反比例函数y=(k<0,x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为12,则k的值为___________.
类型六 利用面积关系列方程求k值
10.如图所示,直线与x轴,y轴分别交于A,B两点,且与反比例函数y=y=(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
A.1 B.2 C.3 D.4
11.如图所示,一次函数y=与反比例函数y=y=的图象交于A,B两点,点C在x轴上,连接AC,BC.若∠ACB=90°,△ABC的面积为20,则k的值是( )
A.-8 B.-10 C.-12 D.-20
12.如图所示,矩形ABCD的顶点A、B在x轴上,且关于y轴对称,反比例函数y=(x>0)的图象经过点C,反比例函数y=(x<0)的图象分别与AD,CD交于点E、F,若S△BEF=7,k1+3k2=0,则k1等于___________.
参考答案
1.D 2. k-1 3. 6 4.C 5.A 6.C 7.C
8.解析(1)如图,过点C,D分别作x轴的垂线,垂足分别为E,F.
∵平行四边形OABC的顶点O为原点,A(-2,-1),B(1,-3),
∴点C的坐标为(3,-2)∴k=3×(-2)=-6.
∴反比例函数的表达式为y=-.
(2)设OB的表达式为y=mx(m≠0),将B(1,-3)代入,得m=-3.
∴OB的表达式为y=-3x.联立y=-与y=-3x,
得,解得x=或x=-(舍去).
将x=代入y=-,得y=-3.∴点D的坐标为(,-3).
(3)∵点C,D都在反比例函数y=(k≠0)的图象上,
∴△ODF的面积=△OCE的面积.
∴△OCD的面积=△ODF的面积+梯形DEC的面积-△OCE的面积=梯形DFEC的面积=×(3+2)×(3-)=.
-12 10. D 11. C 12. 9
_21?????????è?????(www.21cnjy.com)_
专项训练
反比例函数中的面积问题求解技巧
类型一 利用比例系数的几何意义求面积
1.如图所示,A,B是双曲线y=上的两个点,过点A作AC⊥x轴,交OB于点D,垂足为点C.若△ODC的面积为1,D为OB的中点,则k的值为( )
A. B.2 C.4 D.8
2.如图所示,在平面直角坐标系xOy中,四边形OABC为矩形,点A,C分别在x轴,y轴上,点B在函数y1=(x>0,k为常数且k>2)的图象上,边AB与函数y2=(x>0)的图象交于点D,则阴影部分ODBC的面积为_________.(结果用含k的式子表示)
3.如图所示,正比例函数y=-x与反比例函数y=-的图象交于A,C两点,过点A作AB⊥x轴于点B,过点C作CD⊥x轴于点D,则△ABD的面积为__________.
类型二 利用等积变形求面积
4.如图所示,点A在反比例函数y=(x>0)的图象上,过点A作AB⊥x轴,垂足为点B,点C在y轴上,则△ABC的面积为( )
A.3 B.2 C. D.1
5.如图所示,平行于x轴的直线与函数y=(k1>0,x>0),y=(k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的个动点.若△ABC的面积为4,则k1-k2的值为( )
A.8 B.-8 C.4 D.-4
类型三 利用和差法求面积
6.如图所示,点A在双曲线y=上,点B在双曲线y=上,且AB∥x轴,点C,D在x轴上,若四边形ABCD为矩形,则它的面积为( )
A.8 B.6 C.8 D.12
类型四 利用转化法求面积
7.如图所示,在平面直角坐标系中,△OAB的边OA在x轴正半轴上,其中∠OAB=90°,AO=AB,点C为斜边OB的中点,反比例函数y=(k>0,x>0)的图象过点C且交线段AB于点D,连接CD,OD,若S△OCD=,则k的值为( )
A.3 B. C.2 D.1
8.如图所示,平行四边形OABC的顶点C在反比例函数y=(k≠0)的图象上,点O为原点,A(-2,-1),B(1,-3),延长OB交反比例函数y=(k≠0)的图象于点D,连接CD.
(1)求反比例函数的表达式;
(2)求点D的坐标;
(3)试计算△OCD的面积.
类型五 利用割补法求面积
9.如图所示,点A是反比例函数y=(k<0,x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为12,则k的值为___________.
类型六 利用面积关系列方程求k值
10.如图所示,直线与x轴,y轴分别交于A,B两点,且与反比例函数y=y=(x>0)的图象交于点C,若S△AOB=S△BOC=1,则k=( )
A.1 B.2 C.3 D.4
11.如图所示,一次函数y=与反比例函数y=y=的图象交于A,B两点,点C在x轴上,连接AC,BC.若∠ACB=90°,△ABC的面积为20,则k的值是( )
A.-8 B.-10 C.-12 D.-20
12.如图所示,矩形ABCD的顶点A、B在x轴上,且关于y轴对称,反比例函数y=(x>0)的图象经过点C,反比例函数y=(x<0)的图象分别与AD,CD交于点E、F,若S△BEF=7,k1+3k2=0,则k1等于___________.
参考答案
1.D 2. k-1 3. 6 4.C 5.A 6.C 7.C
8.解析(1)如图,过点C,D分别作x轴的垂线,垂足分别为E,F.
∵平行四边形OABC的顶点O为原点,A(-2,-1),B(1,-3),
∴点C的坐标为(3,-2)∴k=3×(-2)=-6.
∴反比例函数的表达式为y=-.
(2)设OB的表达式为y=mx(m≠0),将B(1,-3)代入,得m=-3.
∴OB的表达式为y=-3x.联立y=-与y=-3x,
得,解得x=或x=-(舍去).
将x=代入y=-,得y=-3.∴点D的坐标为(,-3).
(3)∵点C,D都在反比例函数y=(k≠0)的图象上,
∴△ODF的面积=△OCE的面积.
∴△OCD的面积=△ODF的面积+梯形DEC的面积-△OCE的面积=梯形DFEC的面积=×(3+2)×(3-)=.
-12 10. D 11. C 12. 9
_21?????????è?????(www.21cnjy.com)_
