5.7三角函数的应用-【新教材】人教版(2019)高中数学必修第一册同步练习(word含答案)
文档属性
| 名称 | 5.7三角函数的应用-【新教材】人教版(2019)高中数学必修第一册同步练习(word含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 59.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 09:49:16 | ||
图片预览


文档简介
5.7三角函数的应用同步练习
一、单选题
1.某海轮以每小时30海里的速度航行,在点 A 测得海面上油井 P 在南偏东 60? ,海轮向北航行40分钟后到达点 B ,测得油井 P 在南偏东 30? ,海轮改为北偏东 60? 的航向再行驶80分钟到达点 C ,则 P?,?C 两点的距离为( ??)(单位:海里)
A.?207??????????????????????????????????B.?2077??????????????????????????????????C.?203??????????????????????????????????D.?2033
2.在一个港口,相邻两次高潮发生的时间相距12h,低潮时水深为9m,高潮时水深为15m.每天潮涨潮落时,该港口水的深度y(m)关于时间t(h)的函数图象可以近似地看成函数y=Asin(ωt+φ)+k的图象,其中0≤t≤24,且t=3时涨潮到一次高潮,则该函数的解析式可以是(?? )
A.?y=3sinπ6t+12?????????B.?y=?3sinπ6t+12?????????C.?y=3sinπ12t+12?????????D.?y=3cosπ12t+12
3.若sinα+ 3 cosα=2,则tan(π+α)=(?? )
A.?3???????????????????????????????????????B.?2???????????????????????????????????????C.?22???????????????????????????????????????D.?33
4.以长为10的线段AB为直径作半圆,则它内接矩形面积的最大值为( )
A.?10?????????????????????????????????????????B.?15?????????????????????????????????????????C.?25?????????????????????????????????????????D.?50
5.半径为1的球内切于一圆锥,则圆锥体积的最小值为( )
A.?2π???????????????????????????????????????B.?8π3???????????????????????????????????????C.?3π???????????????????????????????????????D.?11π3
6.在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数y1=sint,y2=sint+2π3和y3=sint+4π3描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是( )
A.?仍保持平静???????????????????B.?不断波动???????????????????C.?周期性保持平静???????????????????D.?周期性保持波动
7.M,N是曲线y=πsinx与曲线y=πcosx的两个不同的交点,则|MN|的最小值为( )
A.?π??????????????????????????????????????B.?2π???????????????????????????????????????C.?3π???????????????????????????????????????D.?2π
8.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )
A.?102m?????????????????????????????????B.?20m?????????????????????????????????C.?203m?????????????????????????????????D.?40m
二、填空题
9.在 △ABC 中,两直角边和斜边分别为a,b,c,若 a+b=cx 则实数x的取值范围是________.
10.若电灯B可在过桌面上一点O且垂直于桌面的垂线上移动,桌面上有与点O距离为a的另一点A,问电灯与点0的距离________?,可使点A处有最大的照度?(∠BAO=φ,BA=r,照度与sinφ成正比,与r2成反比)
11.在同一平面直角坐标系中,函数y=cos(x2+3π2)x∈0,2π的图象和直线y=12的交点个数是________ 个
12.点A(x,y)在单位圆上,从A0(12,32)出发,沿逆时针方向做匀速圆周运动,每12秒运动一周.则经过时间t后,y关于t的函数解析式为________?
三、解答题
13.设 △ABC 的三内角 A 、 B 、 C 的对边分别是 a 、 b 、 c ,且 b(sinB?sinC)+(c?a)(sinA+sinC)=0
(Ⅰ)求角 A 的大小;
(Ⅱ)若 a=3 , sinC=1+32sinB ,求 △ABC 的面积.
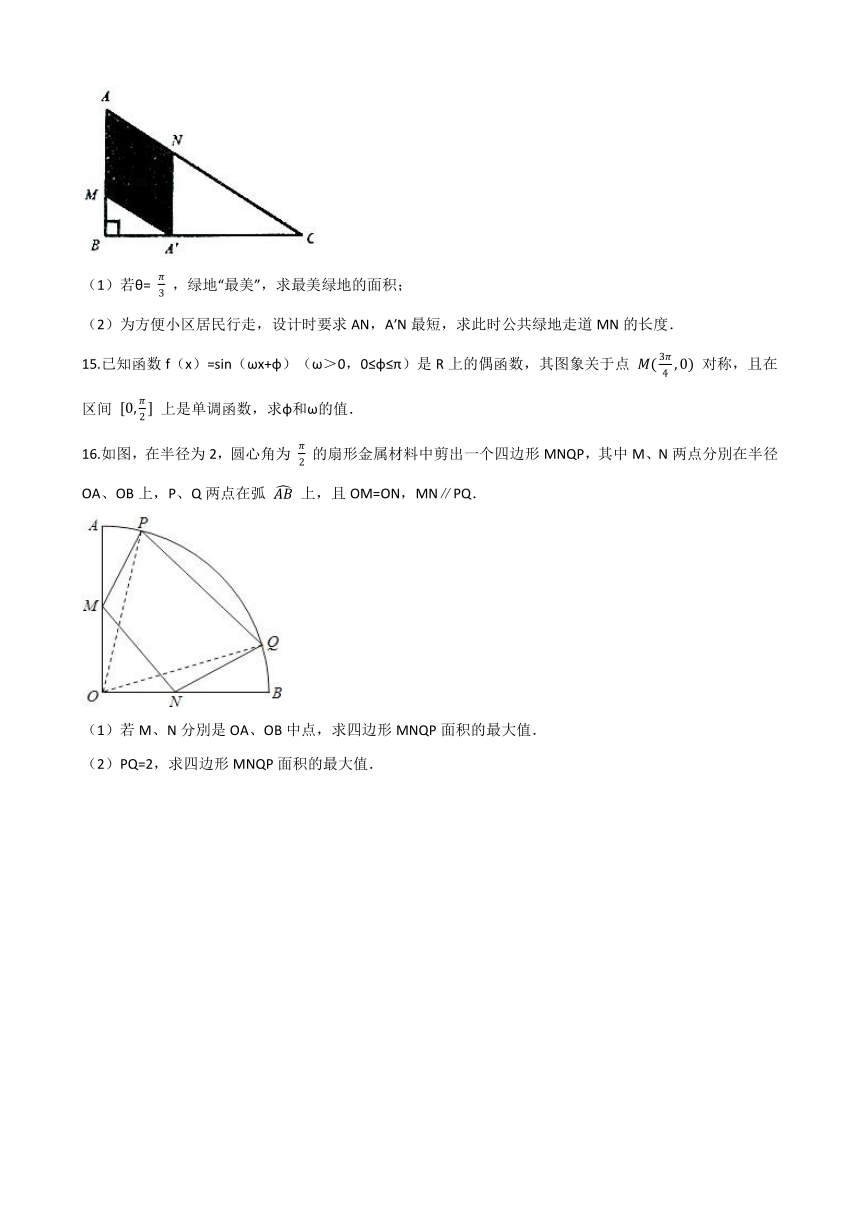
14.如图,某小区准备将一块闲置的直角三角形(其中∠B= π2 ,AB=a,BV= 3 a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.
(1)若θ= π3 ,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民行走,设计时要求AN,A′N最短,求此时公共绿地走道MN的长度.
15.已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点 M(3π4,0) 对称,且在区间 [0,π2] 上是单调函数,求φ和ω的值.
16.如图,在半径为2,圆心角为 π2 的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧 AB 上,且OM=ON,MN∥PQ.
(1)若M、N分別是OA、OB中点,求四边形MNQP面积的最大值.
(2)PQ=2,求四边形MNQP面积的最大值.
参考答案
1. A 2.A 3. D 4. C 5. B 6.A 7. C 8. D 9. (1,2] 10.22a 11.2 12.(π6t+π3)
13.【答案】 解:(Ⅰ)因为 b(sinB?sinC)+(c?a)(sinA+sinC)=0 ,
由正弦定理得 b(b?a)+(c?a)(a+c)=0 ,∴ b2+c2?a2=bc ,?
∴由余弦定理得 cosA=b2+c2?a22bc=12 ,∴在 △ABC 中, A=π3 .
(Ⅱ)方法一:因为 sinC=1+32sinB ,且 A=π3 ,∴ sin(23π?B)=1+32sinB
∴ 32cosB+12sinB=1+32sinB ?,? ∴ tanB=1 ,在 △ABC 中, B=π4
又在 △ABC 中,由正弦定理得 bsinB=asinA=332=2 ,∴ b=2
∴ △ABC 的面积 S=12absinC=12×3×2sin(π4+π3)=622+64=3+34 ?
方法二:因为 sinC=1+32sinB ,由正弦定理得 c=1+32b
而 a=3 , A=π3 ,由余弦定理得 b2+c2?bc=a2 ,∴ b2+(1+3)24b2?1+32b2=3
∴ b2=2 ,即 b=2 , c=2+62
∴ △ABC 的面积 S=12bc?sinA=3+34 ?.
【解析】(I)利用正弦定理将 b(sinB?sinC)+(c?a)(sinA+sinC)=0化简成 b(b?a)+(c?a)(a+c)=0,并利用余弦定理可以计算出cosA值,进而得出答案。(2)根据题目条件和三角形角的和为180度可知,sin(23π?B)=1+32sinB,进而利用正弦两角差公式展开便可以得出角B为π4,再次利用正弦定理bsinB=asinA,可以计算出b的长度,最后结合三角形面积计算公式S=12absinC便可以计算出答案。第二种方法:根据题目条件,利用正弦定理可知道c=1+32b,而a=3,A=π3,由余弦定理得到b2+c2?bc=a2,将b和c的关系式代入该方程,便可以计算出b的长度,利用S=12bc·sinA,得出答案。
14.【答案】 (1)解:由∠B= π2 ,AB=a,BV= 3 a,得∠BAC= π3
设MA=MA′=xa(0<x<1),则MB=a﹣xa,
所以在Rt△MBA′中,cos(π﹣2θ)= a?xaxa = 1?xx
因为θ= π3 ,所以cos(π﹣2θ)= 1?xx = 12 ,所以x= 23 ,
又∠BAC= π3 ,所以△AMN为等边三角形,所以绿地的面积S=2× 12 × 23 a× 23 a×sin π3 = 239a2
(2)解:因为cos(π﹣2θ)═﹣cos2θ=2sin2θ﹣1= 1?xx ,
所以x= 12sin2θ ,则AM= a2sin2θ
又∠BAC= π3 ,所以在△AMN中,∠ANM= 2π3?θ ,故 ANsinθ=AMsin(2π3?θ) ,
所以AN= a2sin2θ × sinθsin(2π3?θ) = a2sinθ?sin(2π3?θ) = a12+sin(2θ?π6)
又 π4<θ<π2 ,所以 π3<2θ?π6<5π6 ,
所以当 2θ?π6=π2 ,即θ= π3 时,AN最短,且AN= 23a ,
此时公共绿地走道MN= 23a
【解析】由∠B= π2 ,AB=a,BV= 3 a,得∠BAC= π3 ,设MA=MA′=xa(0<x<1),则MB=a﹣xa,所以在Rt△MBA′中,cos(π﹣2θ)= a?xaxa = 1?xx ; (1)因为θ= π3 ,所以cos(π﹣2θ)= 1?xx = 12 ,解得x值,可得△AMN为等边三角形,进而得到最美绿地的面积;(2)根据(1)中结论,可得AN= a12+sin(2θ?π6) ,根据三角函数的图象和性质,可得θ= π3 时,AN最短,且AN= 23a ,进而得到答案.
15.【答案】 解:由f(x)是偶函数,得f(﹣x)=f(x),
即sin(﹣ωx+φ)=sin(ωx+φ),
所以﹣cosφsinωx=cosφsinωx,
对任意x都成立,且w>0,
所以得cosφ=0.
依题设0≤φ≤π,所以解得φ= π2 ,
由f(x)的图象关于点M对称,
得 f(3π4?x)=?f(3π4+x) ,
取x=0,得f( 3π4 )=sin( 3ωπ4+π2 )=cos 3ωπ4 ,
∴f( 3π4 )=sin( 3ωπ4+π2 )=cos 3ωπ4 ,
∴cos 3ωπ4 =0,
又w>0,得 3ωπ4 = π2 +kπ,k=0,1,2,3,…
∴ω= 23 (2k+1),k=0,1,2,…
当k=0时,ω= 23 ,f(x)=sin( 23x+π2 )在[0, π2 ]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+ π2 )=cos2x,在[0, π2 ]上是减函数,满足题意;
当k=2时,ω= 103 ,f(x)=sin( 103 x+ π2 )在[0, π2 ]上不是单调函数;
所以,综合得ω= 23 或2
【解析】由f(x)是偶函数可得?的值,图象关于点 M(3π4,0) 对称可得函数关系 f(3π4?x)=?f(3π4+x) ,可得ω的可能取值,结合单调函数可确定ω的值.
16.【答案】 (1)解:连接OP,OQ,则四边形MNQP为梯形.
设∠AOP=∠BOQ=θ∈(0, π4 ),则∠POQ= π2 ﹣2θ,且此时OM=ON=1,
四边形MNQP面积S= 12×2 sinθ+ 12×2 sinθ+ 12×2 ×2sin( π2 ﹣2θ)﹣ 12 =﹣4sin2θ+2sinθ+ 32 ,
∴sinθ= 14 ,S取最大值 74
(2)解:设OM=ON=x∈(0,2),
由PQ=2可知∠POQ= π3 ,∠AOQ=∠BOP= π12 ,
∴sin π12 = 6?24 ,
∴四边形MNQP面积S= 6?24 x+ 6?24 x+ 3 ﹣ 12 x2=﹣ 12 x2+ 6?22 x+ 3 ,
∴x= 6?22 ,S取最大值为 2+32
【解析】(1)设∠AOP=∠BOQ=θ∈(0, π4 ),则∠POQ= π2 ﹣2θ,且此时OM=ON=1,利用分割法,即可求四边形MNQP面积的最大值.(2)PQ=2,可知∠POQ= π3 ,∠AOQ=∠BOP= π12 ,利用分割法,即可求四边形MNQP面积的最大值.
一、单选题
1.某海轮以每小时30海里的速度航行,在点 A 测得海面上油井 P 在南偏东 60? ,海轮向北航行40分钟后到达点 B ,测得油井 P 在南偏东 30? ,海轮改为北偏东 60? 的航向再行驶80分钟到达点 C ,则 P?,?C 两点的距离为( ??)(单位:海里)
A.?207??????????????????????????????????B.?2077??????????????????????????????????C.?203??????????????????????????????????D.?2033
2.在一个港口,相邻两次高潮发生的时间相距12h,低潮时水深为9m,高潮时水深为15m.每天潮涨潮落时,该港口水的深度y(m)关于时间t(h)的函数图象可以近似地看成函数y=Asin(ωt+φ)+k的图象,其中0≤t≤24,且t=3时涨潮到一次高潮,则该函数的解析式可以是(?? )
A.?y=3sinπ6t+12?????????B.?y=?3sinπ6t+12?????????C.?y=3sinπ12t+12?????????D.?y=3cosπ12t+12
3.若sinα+ 3 cosα=2,则tan(π+α)=(?? )
A.?3???????????????????????????????????????B.?2???????????????????????????????????????C.?22???????????????????????????????????????D.?33
4.以长为10的线段AB为直径作半圆,则它内接矩形面积的最大值为( )
A.?10?????????????????????????????????????????B.?15?????????????????????????????????????????C.?25?????????????????????????????????????????D.?50
5.半径为1的球内切于一圆锥,则圆锥体积的最小值为( )
A.?2π???????????????????????????????????????B.?8π3???????????????????????????????????????C.?3π???????????????????????????????????????D.?11π3
6.在一个圆形波浪实验水池的中心有三个振动源,假如不计其它因素,在t秒内,它们引发的水面波动可分别由函数y1=sint,y2=sint+2π3和y3=sint+4π3描述,如果两个振动源同时启动,则水面波动由两个函数的和表达,在某一时刻使这三个振动源同时开始工作,那么,原本平静的水面将呈现的状态是( )
A.?仍保持平静???????????????????B.?不断波动???????????????????C.?周期性保持平静???????????????????D.?周期性保持波动
7.M,N是曲线y=πsinx与曲线y=πcosx的两个不同的交点,则|MN|的最小值为( )
A.?π??????????????????????????????????????B.?2π???????????????????????????????????????C.?3π???????????????????????????????????????D.?2π
8.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为( )
A.?102m?????????????????????????????????B.?20m?????????????????????????????????C.?203m?????????????????????????????????D.?40m
二、填空题
9.在 △ABC 中,两直角边和斜边分别为a,b,c,若 a+b=cx 则实数x的取值范围是________.
10.若电灯B可在过桌面上一点O且垂直于桌面的垂线上移动,桌面上有与点O距离为a的另一点A,问电灯与点0的距离________?,可使点A处有最大的照度?(∠BAO=φ,BA=r,照度与sinφ成正比,与r2成反比)
11.在同一平面直角坐标系中,函数y=cos(x2+3π2)x∈0,2π的图象和直线y=12的交点个数是________ 个
12.点A(x,y)在单位圆上,从A0(12,32)出发,沿逆时针方向做匀速圆周运动,每12秒运动一周.则经过时间t后,y关于t的函数解析式为________?
三、解答题
13.设 △ABC 的三内角 A 、 B 、 C 的对边分别是 a 、 b 、 c ,且 b(sinB?sinC)+(c?a)(sinA+sinC)=0
(Ⅰ)求角 A 的大小;
(Ⅱ)若 a=3 , sinC=1+32sinB ,求 △ABC 的面积.
14.如图,某小区准备将一块闲置的直角三角形(其中∠B= π2 ,AB=a,BV= 3 a)土地开发成公共绿地,设计时,要求绿地部分(图中阴影部分)有公共绿地走道MN,且两边是两个关于走道MN对称的三角形(△AMN和△A′MN),现考虑方便和绿地最大化原则,要求M点与B点不重合,A′点落在边BC上,设∠AMN=θ.
(1)若θ= π3 ,绿地“最美”,求最美绿地的面积;
(2)为方便小区居民行走,设计时要求AN,A′N最短,求此时公共绿地走道MN的长度.
15.已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点 M(3π4,0) 对称,且在区间 [0,π2] 上是单调函数,求φ和ω的值.
16.如图,在半径为2,圆心角为 π2 的扇形金属材料中剪出一个四边形MNQP,其中M、N两点分別在半径OA、OB上,P、Q两点在弧 AB 上,且OM=ON,MN∥PQ.
(1)若M、N分別是OA、OB中点,求四边形MNQP面积的最大值.
(2)PQ=2,求四边形MNQP面积的最大值.
参考答案
1. A 2.A 3. D 4. C 5. B 6.A 7. C 8. D 9. (1,2] 10.22a 11.2 12.(π6t+π3)
13.【答案】 解:(Ⅰ)因为 b(sinB?sinC)+(c?a)(sinA+sinC)=0 ,
由正弦定理得 b(b?a)+(c?a)(a+c)=0 ,∴ b2+c2?a2=bc ,?
∴由余弦定理得 cosA=b2+c2?a22bc=12 ,∴在 △ABC 中, A=π3 .
(Ⅱ)方法一:因为 sinC=1+32sinB ,且 A=π3 ,∴ sin(23π?B)=1+32sinB
∴ 32cosB+12sinB=1+32sinB ?,? ∴ tanB=1 ,在 △ABC 中, B=π4
又在 △ABC 中,由正弦定理得 bsinB=asinA=332=2 ,∴ b=2
∴ △ABC 的面积 S=12absinC=12×3×2sin(π4+π3)=622+64=3+34 ?
方法二:因为 sinC=1+32sinB ,由正弦定理得 c=1+32b
而 a=3 , A=π3 ,由余弦定理得 b2+c2?bc=a2 ,∴ b2+(1+3)24b2?1+32b2=3
∴ b2=2 ,即 b=2 , c=2+62
∴ △ABC 的面积 S=12bc?sinA=3+34 ?.
【解析】(I)利用正弦定理将 b(sinB?sinC)+(c?a)(sinA+sinC)=0化简成 b(b?a)+(c?a)(a+c)=0,并利用余弦定理可以计算出cosA值,进而得出答案。(2)根据题目条件和三角形角的和为180度可知,sin(23π?B)=1+32sinB,进而利用正弦两角差公式展开便可以得出角B为π4,再次利用正弦定理bsinB=asinA,可以计算出b的长度,最后结合三角形面积计算公式S=12absinC便可以计算出答案。第二种方法:根据题目条件,利用正弦定理可知道c=1+32b,而a=3,A=π3,由余弦定理得到b2+c2?bc=a2,将b和c的关系式代入该方程,便可以计算出b的长度,利用S=12bc·sinA,得出答案。
14.【答案】 (1)解:由∠B= π2 ,AB=a,BV= 3 a,得∠BAC= π3
设MA=MA′=xa(0<x<1),则MB=a﹣xa,
所以在Rt△MBA′中,cos(π﹣2θ)= a?xaxa = 1?xx
因为θ= π3 ,所以cos(π﹣2θ)= 1?xx = 12 ,所以x= 23 ,
又∠BAC= π3 ,所以△AMN为等边三角形,所以绿地的面积S=2× 12 × 23 a× 23 a×sin π3 = 239a2
(2)解:因为cos(π﹣2θ)═﹣cos2θ=2sin2θ﹣1= 1?xx ,
所以x= 12sin2θ ,则AM= a2sin2θ
又∠BAC= π3 ,所以在△AMN中,∠ANM= 2π3?θ ,故 ANsinθ=AMsin(2π3?θ) ,
所以AN= a2sin2θ × sinθsin(2π3?θ) = a2sinθ?sin(2π3?θ) = a12+sin(2θ?π6)
又 π4<θ<π2 ,所以 π3<2θ?π6<5π6 ,
所以当 2θ?π6=π2 ,即θ= π3 时,AN最短,且AN= 23a ,
此时公共绿地走道MN= 23a
【解析】由∠B= π2 ,AB=a,BV= 3 a,得∠BAC= π3 ,设MA=MA′=xa(0<x<1),则MB=a﹣xa,所以在Rt△MBA′中,cos(π﹣2θ)= a?xaxa = 1?xx ; (1)因为θ= π3 ,所以cos(π﹣2θ)= 1?xx = 12 ,解得x值,可得△AMN为等边三角形,进而得到最美绿地的面积;(2)根据(1)中结论,可得AN= a12+sin(2θ?π6) ,根据三角函数的图象和性质,可得θ= π3 时,AN最短,且AN= 23a ,进而得到答案.
15.【答案】 解:由f(x)是偶函数,得f(﹣x)=f(x),
即sin(﹣ωx+φ)=sin(ωx+φ),
所以﹣cosφsinωx=cosφsinωx,
对任意x都成立,且w>0,
所以得cosφ=0.
依题设0≤φ≤π,所以解得φ= π2 ,
由f(x)的图象关于点M对称,
得 f(3π4?x)=?f(3π4+x) ,
取x=0,得f( 3π4 )=sin( 3ωπ4+π2 )=cos 3ωπ4 ,
∴f( 3π4 )=sin( 3ωπ4+π2 )=cos 3ωπ4 ,
∴cos 3ωπ4 =0,
又w>0,得 3ωπ4 = π2 +kπ,k=0,1,2,3,…
∴ω= 23 (2k+1),k=0,1,2,…
当k=0时,ω= 23 ,f(x)=sin( 23x+π2 )在[0, π2 ]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+ π2 )=cos2x,在[0, π2 ]上是减函数,满足题意;
当k=2时,ω= 103 ,f(x)=sin( 103 x+ π2 )在[0, π2 ]上不是单调函数;
所以,综合得ω= 23 或2
【解析】由f(x)是偶函数可得?的值,图象关于点 M(3π4,0) 对称可得函数关系 f(3π4?x)=?f(3π4+x) ,可得ω的可能取值,结合单调函数可确定ω的值.
16.【答案】 (1)解:连接OP,OQ,则四边形MNQP为梯形.
设∠AOP=∠BOQ=θ∈(0, π4 ),则∠POQ= π2 ﹣2θ,且此时OM=ON=1,
四边形MNQP面积S= 12×2 sinθ+ 12×2 sinθ+ 12×2 ×2sin( π2 ﹣2θ)﹣ 12 =﹣4sin2θ+2sinθ+ 32 ,
∴sinθ= 14 ,S取最大值 74
(2)解:设OM=ON=x∈(0,2),
由PQ=2可知∠POQ= π3 ,∠AOQ=∠BOP= π12 ,
∴sin π12 = 6?24 ,
∴四边形MNQP面积S= 6?24 x+ 6?24 x+ 3 ﹣ 12 x2=﹣ 12 x2+ 6?22 x+ 3 ,
∴x= 6?22 ,S取最大值为 2+32
【解析】(1)设∠AOP=∠BOQ=θ∈(0, π4 ),则∠POQ= π2 ﹣2θ,且此时OM=ON=1,利用分割法,即可求四边形MNQP面积的最大值.(2)PQ=2,可知∠POQ= π3 ,∠AOQ=∠BOP= π12 ,利用分割法,即可求四边形MNQP面积的最大值.
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
