第二十九章 投影与视图 《29.1 投影》同步练习2020-2021学年数学人教版九年级下册(word版含解析)
文档属性
| 名称 | 第二十九章 投影与视图 《29.1 投影》同步练习2020-2021学年数学人教版九年级下册(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 218.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-04 00:00:00 | ||
图片预览

文档简介
《29.1 投影》同步练习2020-2021年数学人教版九(下)
一.选择题(共10小题)
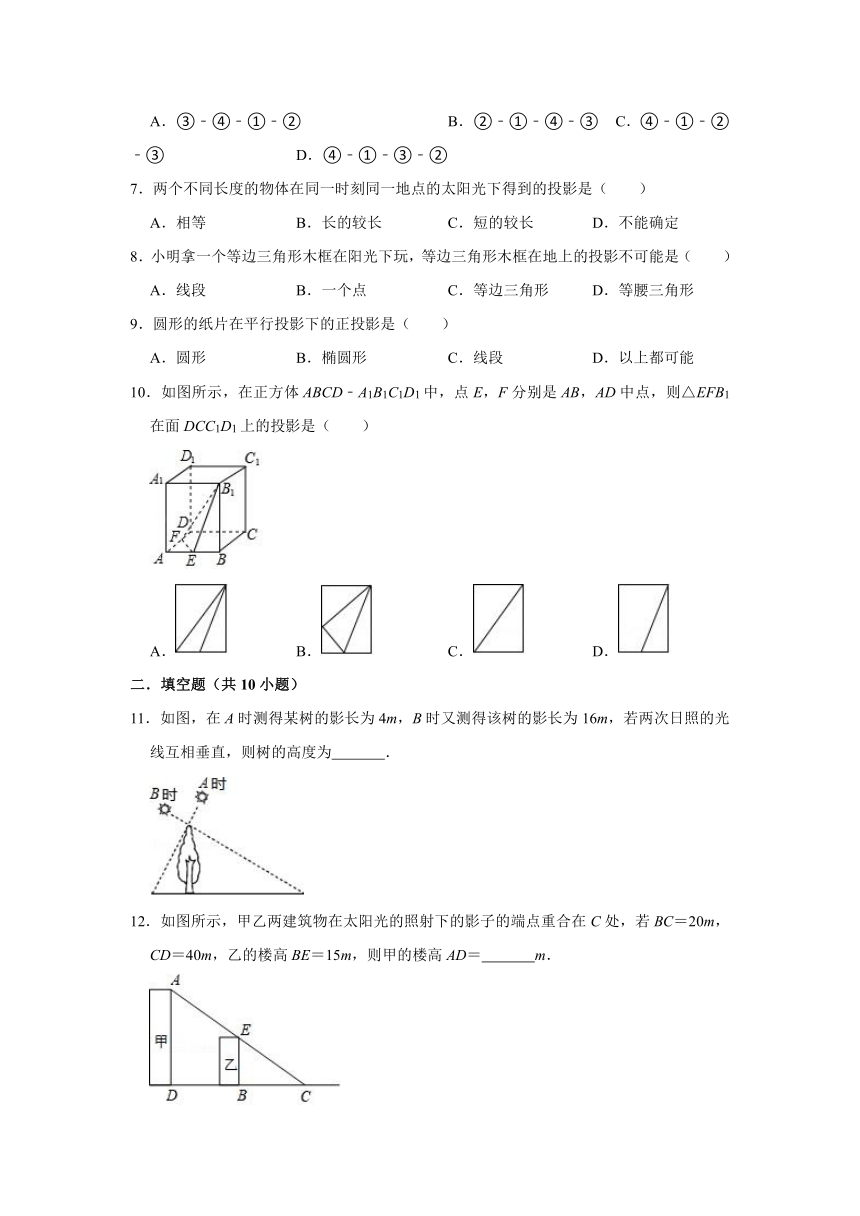
1.如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )
A.①②③④ B.④③②① C.④③①② D.②③④①
2.一张矩形纸片在太阳光线的照射下,形成影子不可能是( )
A.平行四边形 B.矩形 C.正方形 D.梯形
3.太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B.15 C.10 D.
4.下列命题中,真命题有( )
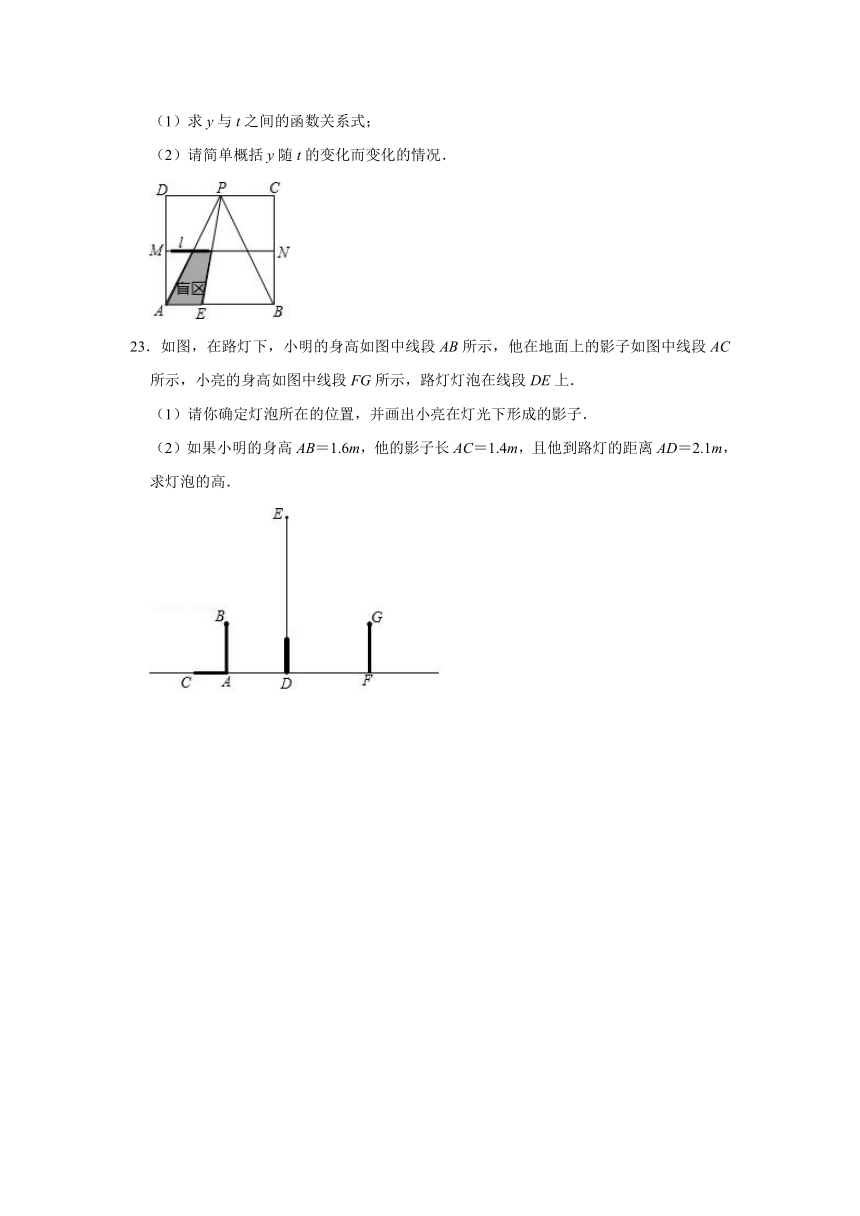
①正方形的平行投影一定是菱形;②平行四边形的平行投影一定是平行四边形;③三角形的平行投影一定是三角形.
A.0个 B.1个 C.2个 D.3个
5.在平行投影下,矩形的投影不可能是( )
A. B. C. D.
6.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③﹣④﹣①﹣② B.②﹣①﹣④﹣③ C.④﹣①﹣②﹣③ D.④﹣①﹣③﹣②
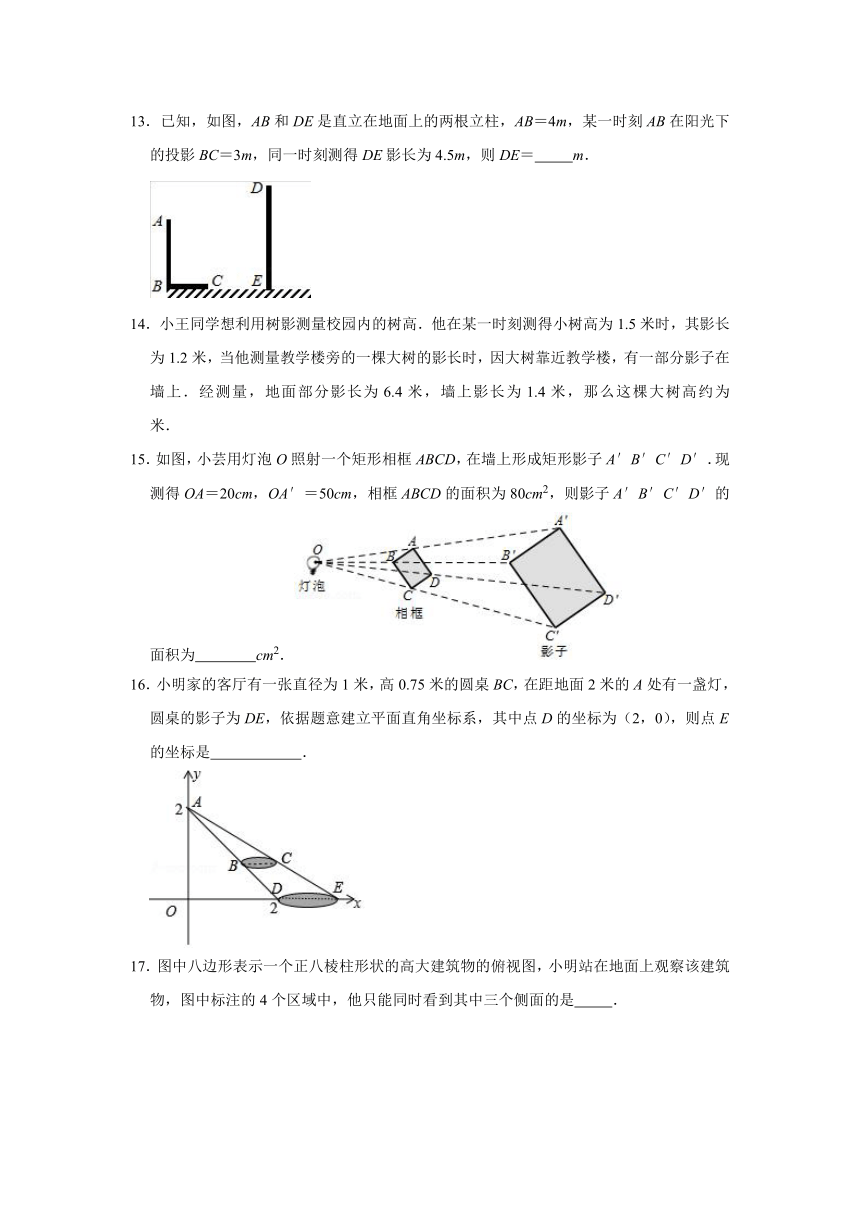
7.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是( )
A.相等 B.长的较长 C.短的较长 D.不能确定
8.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地上的投影不可能是( )
A.线段 B.一个点 C.等边三角形 D.等腰三角形
9.圆形的纸片在平行投影下的正投影是( )
A.圆形 B.椭圆形 C.线段 D.以上都可能
10.如图所示,在正方体ABCD﹣A1B1C1D1中,点E,F分别是AB,AD中点,则△EFB1在面DCC1D1上的投影是( )
A. B. C. D.
二.填空题(共10小题)
11.如图,在A时测得某树的影长为4m,B时又测得该树的影长为16m,若两次日照的光线互相垂直,则树的高度为 .
12.如图所示,甲乙两建筑物在太阳光的照射下的影子的端点重合在C处,若BC=20m,CD=40m,乙的楼高BE=15m,则甲的楼高AD= m.
13.已知,如图,AB和DE是直立在地面上的两根立柱,AB=4m,某一时刻AB在阳光下的投影BC=3m,同一时刻测得DE影长为4.5m,则DE= m.
14.小王同学想利用树影测量校园内的树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树的影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高约为 米.
15.如图,小芸用灯泡O照射一个矩形相框ABCD,在墙上形成矩形影子A′B′C′D′.现测得OA=20cm,OA′=50cm,相框ABCD的面积为80cm2,则影子A′B′C′D′的面积为 cm2.
16.小明家的客厅有一张直径为1米,高0.75米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 .
17.图中八边形表示一个正八棱柱形状的高大建筑物的俯视图,小明站在地面上观察该建筑物,图中标注的4个区域中,他只能同时看到其中三个侧面的是 .
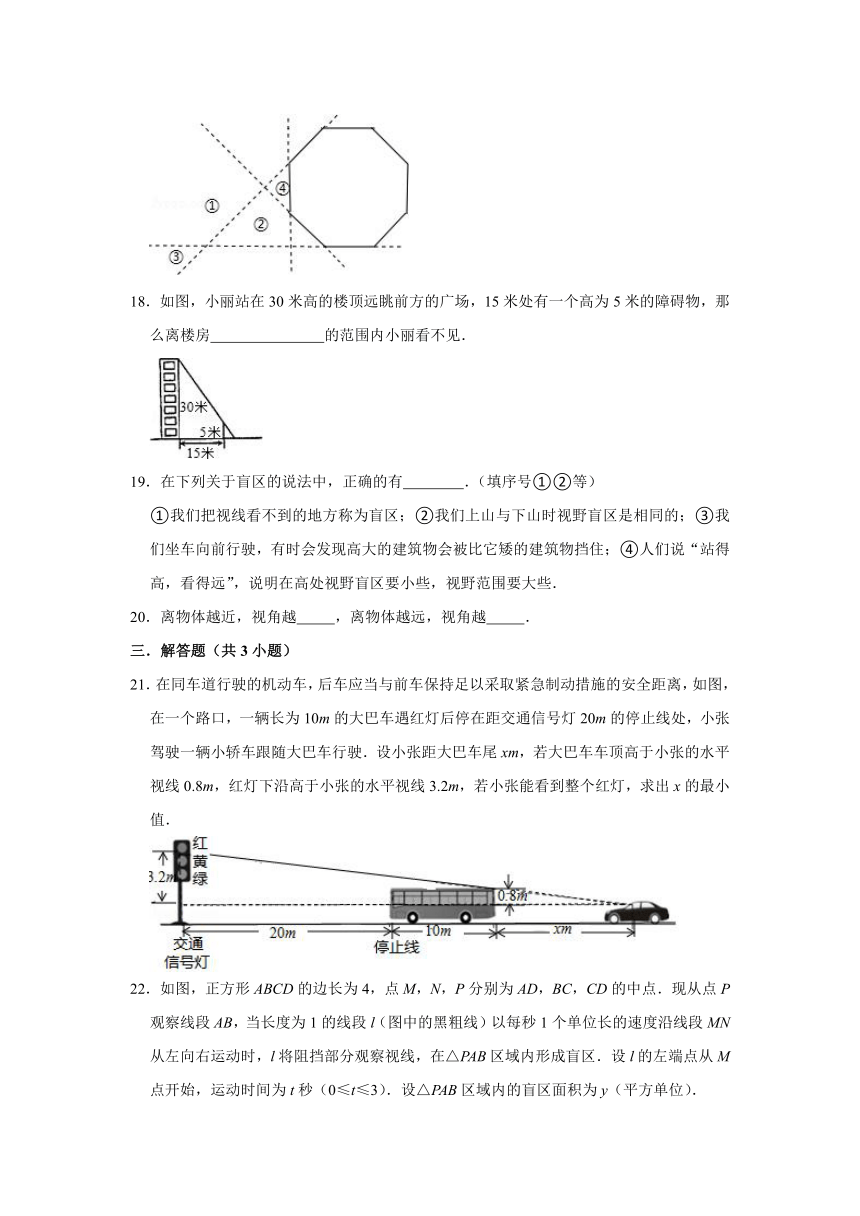
18.如图,小丽站在30米高的楼顶远眺前方的广场,15米处有一个高为5米的障碍物,那么离楼房 的范围内小丽看不见.
19.在下列关于盲区的说法中,正确的有 .(填序号①②等)
①我们把视线看不到的地方称为盲区;②我们上山与下山时视野盲区是相同的;③我们坐车向前行驶,有时会发现高大的建筑物会被比它矮的建筑物挡住;④人们说“站得高,看得远”,说明在高处视野盲区要小些,视野范围要大些.
20.离物体越近,视角越 ,离物体越远,视角越 .
三.解答题(共3小题)
21.在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾xm,若大巴车车顶高于小张的水平视线0.8m,红灯下沿高于小张的水平视线3.2m,若小张能看到整个红灯,求出x的最小值.
22.如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的左端点从M点开始,运动时间为t秒(0≤t≤3).设△PAB区域内的盲区面积为y(平方单位).
(1)求y与t之间的函数关系式;
(2)请简单概括y随t的变化而变化的情况.
23.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
参考答案
一.选择题(共10小题)
1.解:根据平行投影的规律知:顺序为④③①②.
故选:C.
2.解:一张矩形纸片在太阳光线的照射下,形成影子不可能是梯形,
故选:D.
3.解:由题意得:DC=2R,DE=10,∠CED=60°,
∴可得:DC=DEsin60°=15.
故选:B.
4.解:在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变.因不知道光线的方向,故三个选项均错误.
故选:A.
5.解:在平行投影下,矩形的投影可能是直线、矩形、平行四边形,
不可能是直角梯形,
故选:A.
6.解:根据影子的位置和长度,可以判断照片的先后顺序,
早晨太阳在东方,树的影子在树的西方,影长较长,随时间的推移,影子的位置依次经过西北、北、东北、东,
影长先逐渐变短,随后又逐渐变长,
故顺序为:②①④③,
故选:B.
7.解:由于不知道两个物体的摆放情况,无法比较两物体.故选:D.
8.解:当等边三角形木框与阳光平行时,投影是线段;
当等边三角形木框与阳光垂直时,投影是等边三角形;
当等边三角形木框与阳光有一定角度时,投影是等腰三角形;
投影不可能是一个点.
故选:B.
9.解:圆形的纸片在平行投影下的正投影可能是圆形、椭圆形、线段,
故选:D.
10.解:共线图形可知:△EFB1在面DCC1D1上的投影是选项A,
故选:A.
二.填空题(共10小题)
11.解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED?FD,
代入数据可得DC2=64,
DC=8;
故答案为:8m.
12.解:根据题意得AD∥BE,
∴△CBE∽△CDA,
∴=,即=,
∴DA=30(m).
故答案为30.
13.解:DE在阳光下的投影是EF如图所示;
在测量AB的投影时,同时测量出DE在阳光下的投影长为4.5m,
∵△ABC∽△DEF,AB=4m,BC=3m,EF=4.5m,
∴=,
∴=,
∴DE=6(m)
故答案是:6.
14.解:设这棵大树高为x,
根据平行投影特点:在同一时刻,不同物体的物高和影长成比例.
可得树高比影长为=1.25,
则有==0.8,
解可得:x=9.4米.
15.解:∵OA:OA′=2:5,
可知OB:OB′=2:5,
∵∠AOB=∠A′OB′,
∴△AOB∽△A′OB′,
∴AB:A′B′=2:5,
∴矩形ABCD的面积:矩形A′B′C′D′的面积为4:25,
又矩形ABCD的面积为80cm2,则矩形A′B′C′D′的面积为500cm2.
故答案为:500cm2.
16.解:过点B作BF⊥x轴,垂足为F,由题意得,BF=0.75,BC=1,
∵BC∥DE,
∴△ABC∽△ADE,
∴==,
即:=,
解得:DE=1.6,
∴OE=2+1.6=3.6,
∴E(3.6,0),
故答案为:(3.6,0).
17.解:从①的角度也只能看到3个侧面,
从②的角度也只能看到两个侧面,
从③的角度能看到4个侧面;
从④的角度只能看到一个侧面.
只有①的角度才能看到三个侧面.
故答案为:①.
18.解:由题意得,盲区为BD,
设BD=x,则BC=x+15,
∴=,
解得:x=3,
∴在大于15米小于18米的范围内小丽看不见.
故答案为:大于15米小于18米.
19.解:②中上山和下山时盲区是不同的,要记住仰视时越向前视野越小盲区越大,俯视时越向前视野越大,盲区越小.
而①③④都是正确的,因此选①③④.
20.解:离物体越近,视角越大,离物体越远,视角越小.
故答案是:大;小.
三.解答题(共3小题)
21.解:如图,由题可得CD∥AB,
∴△OCD∽△OAB,
∴=,
即=,
解得x=10,
∴x的最小值为10.
22.解:(1)∵正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点,
∴AM=2,盲区为梯形,且上底为下底的一半,高为2,
当0≤t≤1时,y=(t+2t)?2=3t,
当1<t≤2时,y=(1+2)×2=3,
当2<t≤3时,y=[3﹣t+2(3﹣t)]?2=9﹣3t;
(2)1秒内,y随t的增大而增大;1秒到2秒,y的值不变;2秒到3秒,y随t的增大而减小.
23.(1)解:如图,点O为灯泡所在的位置,
线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,=,
∴=,
∴OD=4.
∴灯泡的高为4m.
一.选择题(共10小题)
1.如图是小明一天看到的一根电线杆的影子的俯视图,按时间先后顺序排列正确的是( )
A.①②③④ B.④③②① C.④③①② D.②③④①
2.一张矩形纸片在太阳光线的照射下,形成影子不可能是( )
A.平行四边形 B.矩形 C.正方形 D.梯形
3.太阳光线与地面成60°的角,照射在地面上的一只皮球上,皮球在地面上的投影长是,则皮球的直径是( )
A. B.15 C.10 D.
4.下列命题中,真命题有( )
①正方形的平行投影一定是菱形;②平行四边形的平行投影一定是平行四边形;③三角形的平行投影一定是三角形.
A.0个 B.1个 C.2个 D.3个
5.在平行投影下,矩形的投影不可能是( )
A. B. C. D.
6.如图是一棵小树一天内在太阳下不同时刻的照片,将它们按时间先后顺序进行排列正确的是( )
A.③﹣④﹣①﹣② B.②﹣①﹣④﹣③ C.④﹣①﹣②﹣③ D.④﹣①﹣③﹣②
7.两个不同长度的物体在同一时刻同一地点的太阳光下得到的投影是( )
A.相等 B.长的较长 C.短的较长 D.不能确定
8.小明拿一个等边三角形木框在阳光下玩,等边三角形木框在地上的投影不可能是( )
A.线段 B.一个点 C.等边三角形 D.等腰三角形
9.圆形的纸片在平行投影下的正投影是( )
A.圆形 B.椭圆形 C.线段 D.以上都可能
10.如图所示,在正方体ABCD﹣A1B1C1D1中,点E,F分别是AB,AD中点,则△EFB1在面DCC1D1上的投影是( )
A. B. C. D.
二.填空题(共10小题)
11.如图,在A时测得某树的影长为4m,B时又测得该树的影长为16m,若两次日照的光线互相垂直,则树的高度为 .
12.如图所示,甲乙两建筑物在太阳光的照射下的影子的端点重合在C处,若BC=20m,CD=40m,乙的楼高BE=15m,则甲的楼高AD= m.
13.已知,如图,AB和DE是直立在地面上的两根立柱,AB=4m,某一时刻AB在阳光下的投影BC=3m,同一时刻测得DE影长为4.5m,则DE= m.
14.小王同学想利用树影测量校园内的树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树的影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高约为 米.
15.如图,小芸用灯泡O照射一个矩形相框ABCD,在墙上形成矩形影子A′B′C′D′.现测得OA=20cm,OA′=50cm,相框ABCD的面积为80cm2,则影子A′B′C′D′的面积为 cm2.
16.小明家的客厅有一张直径为1米,高0.75米的圆桌BC,在距地面2米的A处有一盏灯,圆桌的影子为DE,依据题意建立平面直角坐标系,其中点D的坐标为(2,0),则点E的坐标是 .
17.图中八边形表示一个正八棱柱形状的高大建筑物的俯视图,小明站在地面上观察该建筑物,图中标注的4个区域中,他只能同时看到其中三个侧面的是 .
18.如图,小丽站在30米高的楼顶远眺前方的广场,15米处有一个高为5米的障碍物,那么离楼房 的范围内小丽看不见.
19.在下列关于盲区的说法中,正确的有 .(填序号①②等)
①我们把视线看不到的地方称为盲区;②我们上山与下山时视野盲区是相同的;③我们坐车向前行驶,有时会发现高大的建筑物会被比它矮的建筑物挡住;④人们说“站得高,看得远”,说明在高处视野盲区要小些,视野范围要大些.
20.离物体越近,视角越 ,离物体越远,视角越 .
三.解答题(共3小题)
21.在同车道行驶的机动车,后车应当与前车保持足以采取紧急制动措施的安全距离,如图,在一个路口,一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处,小张驾驶一辆小轿车跟随大巴车行驶.设小张距大巴车尾xm,若大巴车车顶高于小张的水平视线0.8m,红灯下沿高于小张的水平视线3.2m,若小张能看到整个红灯,求出x的最小值.
22.如图,正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点.现从点P观察线段AB,当长度为1的线段l(图中的黑粗线)以每秒1个单位长的速度沿线段MN从左向右运动时,l将阻挡部分观察视线,在△PAB区域内形成盲区.设l的左端点从M点开始,运动时间为t秒(0≤t≤3).设△PAB区域内的盲区面积为y(平方单位).
(1)求y与t之间的函数关系式;
(2)请简单概括y随t的变化而变化的情况.
23.如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.
(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
参考答案
一.选择题(共10小题)
1.解:根据平行投影的规律知:顺序为④③①②.
故选:C.
2.解:一张矩形纸片在太阳光线的照射下,形成影子不可能是梯形,
故选:D.
3.解:由题意得:DC=2R,DE=10,∠CED=60°,
∴可得:DC=DEsin60°=15.
故选:B.
4.解:在不同时刻,同一物体的影子的方向和大小可能不同,不同时刻物体在太阳光下的影子的大小在变,方向也在改变.因不知道光线的方向,故三个选项均错误.
故选:A.
5.解:在平行投影下,矩形的投影可能是直线、矩形、平行四边形,
不可能是直角梯形,
故选:A.
6.解:根据影子的位置和长度,可以判断照片的先后顺序,
早晨太阳在东方,树的影子在树的西方,影长较长,随时间的推移,影子的位置依次经过西北、北、东北、东,
影长先逐渐变短,随后又逐渐变长,
故顺序为:②①④③,
故选:B.
7.解:由于不知道两个物体的摆放情况,无法比较两物体.故选:D.
8.解:当等边三角形木框与阳光平行时,投影是线段;
当等边三角形木框与阳光垂直时,投影是等边三角形;
当等边三角形木框与阳光有一定角度时,投影是等腰三角形;
投影不可能是一个点.
故选:B.
9.解:圆形的纸片在平行投影下的正投影可能是圆形、椭圆形、线段,
故选:D.
10.解:共线图形可知:△EFB1在面DCC1D1上的投影是选项A,
故选:A.
二.填空题(共10小题)
11.解:如图:过点C作CD⊥EF,
由题意得:△EFC是直角三角形,∠ECF=90°,
∴∠EDC=∠CDF=90°,
∴∠E+∠ECD=∠ECD+∠DCF=90°,
∴∠E=∠DCF,
∴Rt△EDC∽Rt△CDF,
有=;即DC2=ED?FD,
代入数据可得DC2=64,
DC=8;
故答案为:8m.
12.解:根据题意得AD∥BE,
∴△CBE∽△CDA,
∴=,即=,
∴DA=30(m).
故答案为30.
13.解:DE在阳光下的投影是EF如图所示;
在测量AB的投影时,同时测量出DE在阳光下的投影长为4.5m,
∵△ABC∽△DEF,AB=4m,BC=3m,EF=4.5m,
∴=,
∴=,
∴DE=6(m)
故答案是:6.
14.解:设这棵大树高为x,
根据平行投影特点:在同一时刻,不同物体的物高和影长成比例.
可得树高比影长为=1.25,
则有==0.8,
解可得:x=9.4米.
15.解:∵OA:OA′=2:5,
可知OB:OB′=2:5,
∵∠AOB=∠A′OB′,
∴△AOB∽△A′OB′,
∴AB:A′B′=2:5,
∴矩形ABCD的面积:矩形A′B′C′D′的面积为4:25,
又矩形ABCD的面积为80cm2,则矩形A′B′C′D′的面积为500cm2.
故答案为:500cm2.
16.解:过点B作BF⊥x轴,垂足为F,由题意得,BF=0.75,BC=1,
∵BC∥DE,
∴△ABC∽△ADE,
∴==,
即:=,
解得:DE=1.6,
∴OE=2+1.6=3.6,
∴E(3.6,0),
故答案为:(3.6,0).
17.解:从①的角度也只能看到3个侧面,
从②的角度也只能看到两个侧面,
从③的角度能看到4个侧面;
从④的角度只能看到一个侧面.
只有①的角度才能看到三个侧面.
故答案为:①.
18.解:由题意得,盲区为BD,
设BD=x,则BC=x+15,
∴=,
解得:x=3,
∴在大于15米小于18米的范围内小丽看不见.
故答案为:大于15米小于18米.
19.解:②中上山和下山时盲区是不同的,要记住仰视时越向前视野越小盲区越大,俯视时越向前视野越大,盲区越小.
而①③④都是正确的,因此选①③④.
20.解:离物体越近,视角越大,离物体越远,视角越小.
故答案是:大;小.
三.解答题(共3小题)
21.解:如图,由题可得CD∥AB,
∴△OCD∽△OAB,
∴=,
即=,
解得x=10,
∴x的最小值为10.
22.解:(1)∵正方形ABCD的边长为4,点M,N,P分别为AD,BC,CD的中点,
∴AM=2,盲区为梯形,且上底为下底的一半,高为2,
当0≤t≤1时,y=(t+2t)?2=3t,
当1<t≤2时,y=(1+2)×2=3,
当2<t≤3时,y=[3﹣t+2(3﹣t)]?2=9﹣3t;
(2)1秒内,y随t的增大而增大;1秒到2秒,y的值不变;2秒到3秒,y随t的增大而减小.
23.(1)解:如图,点O为灯泡所在的位置,
线段FH为小亮在灯光下形成的影子.
(2)解:由已知可得,=,
∴=,
∴OD=4.
∴灯泡的高为4m.
