第二十九章 投影与视图《29.3 课题学习 制作立体模型》同步练习2020-2021学年数学人教版九 年级下册(word版含解析)
文档属性
| 名称 | 第二十九章 投影与视图《29.3 课题学习 制作立体模型》同步练习2020-2021学年数学人教版九 年级下册(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 135.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-04 13:58:14 | ||
图片预览


文档简介
《29.3 课题学习 制作立体模型》同步练习2020-2021年数学人教版九(下)
一.选择题(共13小题)
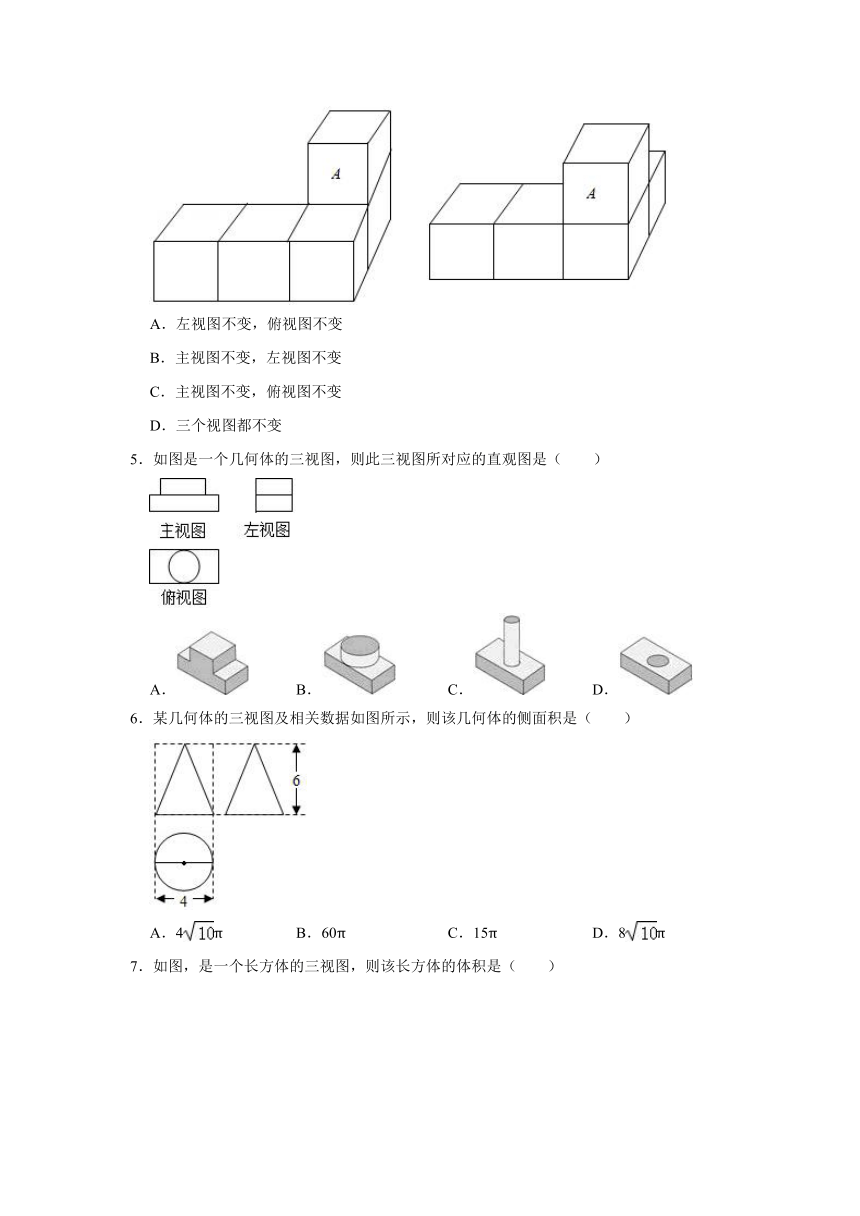
1.如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,则该几何体的主视图是( )
A. B. C. D.
2.如图是由若干个棱长为1的小正方体搭成的一个几何体的三视图,则这个几何体的体积是( )
A.5 B.6 C.8 D.12
3.如图,已知圆锥的三视图所示,则这个圆锥的侧面展开图扇形的圆心角的度数为( )
A.270° B.216° C.108° D.135°
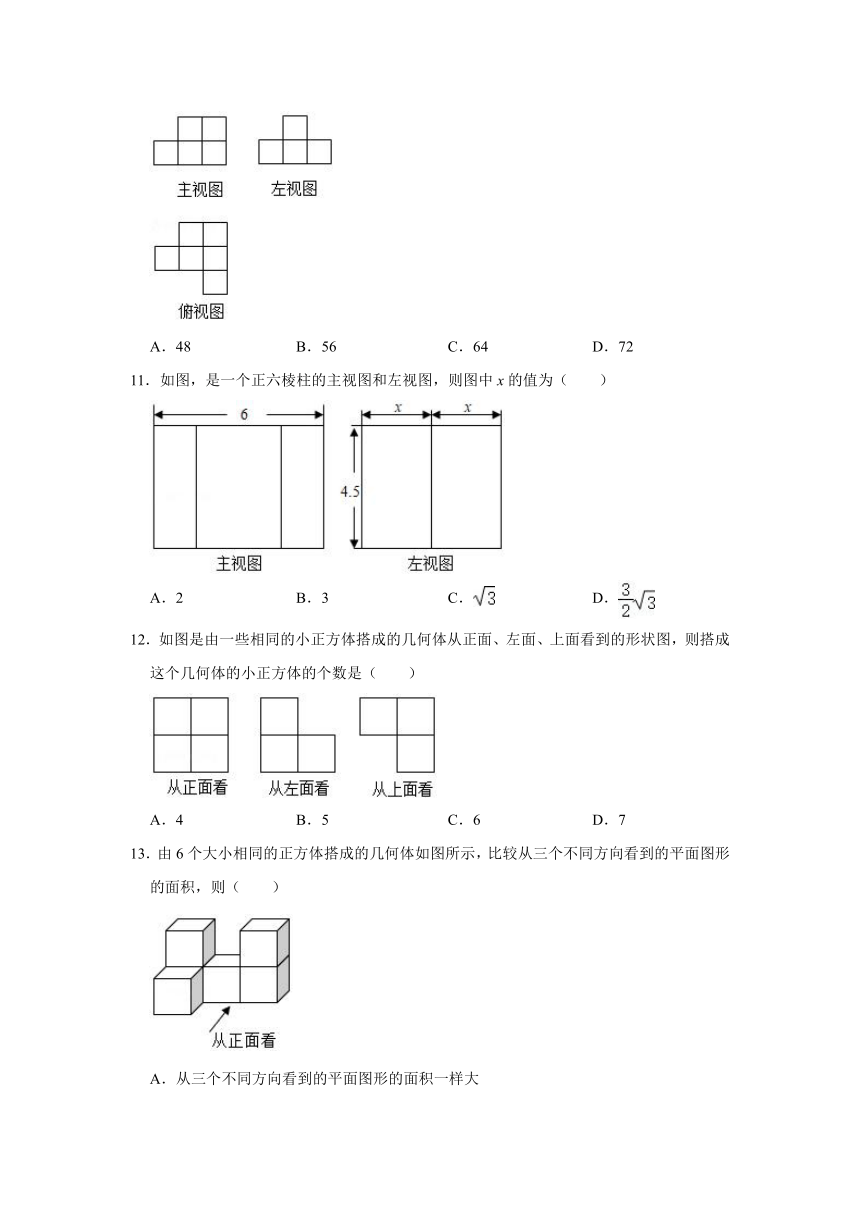
4.如图,是由5个大小一样的立方体摆放而成的,移动立方体A,由图1变化至图2,那么由图1的三视图变化至图2的三视图中,则( )
A.左视图不变,俯视图不变
B.主视图不变,左视图不变
C.主视图不变,俯视图不变
D.三个视图都不变
5.如图是一个几何体的三视图,则此三视图所对应的直观图是( )
A. B. C. D.
6.某几何体的三视图及相关数据如图所示,则该几何体的侧面积是( )
A.4π B.60π C.15π D.8π
7.如图,是一个长方体的三视图,则该长方体的体积是( )
A.m3﹣3m2+2m B.m3﹣2m C.m3+m2﹣2m D.m3+m2﹣m
8.如图是由六个大小相同的小正方体搭成的几何体的俯视图,则该几何体的左视图不可能是( )
A. B.
C. D.
9.一个几何体由若干个大小相同的小正方体组成,它的俯视图和左视图如图所示,则构成这个几何体的小正方体的个数最多为( )
A.4个 B.5个 C.6个 D.7个
10.如图是由若干个棱长为2的小正方体搭成的物体的三个视图,则这个物体的体积为( )
A.48 B.56 C.64 D.72
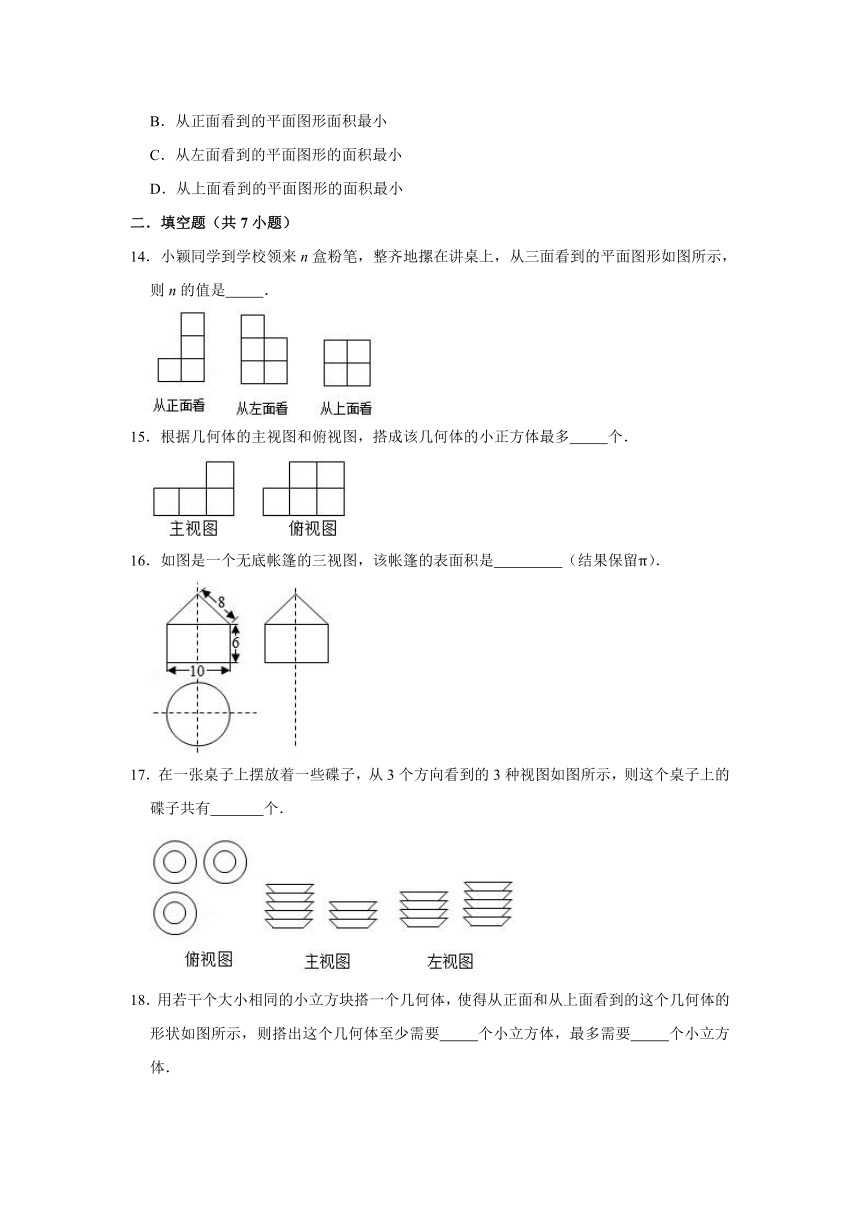
11.如图,是一个正六棱柱的主视图和左视图,则图中x的值为( )
A.2 B.3 C. D.
12.如图是由一些相同的小正方体搭成的几何体从正面、左面、上面看到的形状图,则搭成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.7
13.由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A.从三个不同方向看到的平面图形的面积一样大
B.从正面看到的平面图形面积最小
C.从左面看到的平面图形的面积最小
D.从上面看到的平面图形的面积最小
二.填空题(共7小题)
14.小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,从三面看到的平面图形如图所示,则n的值是 .
15.根据几何体的主视图和俯视图,搭成该几何体的小正方体最多 个.
16.如图是一个无底帐篷的三视图,该帐篷的表面积是 (结果保留π).
17.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有 个.
18.用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示,则搭出这个几何体至少需要 个小立方体,最多需要 个小立方体.
19.如图,是由几个边长为1的小立方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,则这个几何体的表面积为 .
20.如图放置的一个圆锥,它的主视图是边长为2的等边三角形,则该圆锥的侧面积为 (结果保留π)
参考答案
一.选择题(共13小题)
1.解:观察图形可知,该几何体的主视图是.
故选:A.
2.解:综合三视图,我们可以得出,这个几何模型的底层有3+1=5个小正方体,第二层有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是5+1=6个.
∴这个几何体的体积是6×13=6,
故选:B.
3.解:观察三视图得:圆锥的底面半径为3cm,高为4cm,
所以圆锥的母线长为5cm,
=6π,解得n=216°.
故选:B.
4.解:主视图都是第一层三个正方形,第二层右边一个正方形,故主视图不变;
左视图都是第一层两个正方形,正方形位置发生了变化,故左视图改变;
俯视图底层的正方形没有变化,故俯视图不变.
∴主视图不变,俯视图不变.
故选:C.
5.解:由图可得,此三视图所对应的直观图是.
故选:B.
6.解:观察图形可知:
圆锥母线长为:=2,
所以圆锥侧面积为:πrl=2×2×π=4π.
故选:A.
7.解:观察三视图发现该长方体的长、宽、高分别为m+2、m、m﹣1,
依题意可求出该几何体的体积为(m+2)?m?(m﹣1)=m3+m2﹣2m.
故选:C.
8.解:根据俯视图可得,左视图有三列,第2层只能有一个,
故选:B.
9.解:由俯视图与左视图知,该几何体所需小正方体个数最多分布情况如下图所示:
故选:D.
10.解:由三视图可知,物体由8个小正方体堆积而成,其中第一排最右边有一个正方体,第二排最左边有一个正方体,中间有两个正方体上下堆积,第三排中间有一个正方体,最右边有一个正方体,
右图为该物体的俯视图,每个正方体里面的数字为该位置小正方体的个数,一共有8个小正方体,每个棱长为2,故每个小正方体的体积为2×2×2=8.
故该物体的体积为:8×8=64.
故选:C.
11.解:正六棱柱的底面如图所示,过点A作AH⊥BC于H.
由题意得,2AH+BD=6,
∵∠BAC=120°,AC=AB,
∴∠CAH=∠BAH=60°,
∴∠ABH=30°,
∴AB=2AH,
∴4AH=6,
∴AH=,
∴BH=AH=,
∴x的值为,
故选:D.
12.解:从主视图和俯视图可知,几何体的底层有3个正方体,
从主视图和左视图可知,几何体的第二层有2个正方体,
则搭成这个几何体的小正方体的个数为:3+2=5,
故选:B.
13.解:主视图有5个小正方形,左视图有3个小正方形,俯视图有4个小正方形,
从左面看图形面积最小.
故选:C.
二.填空题(共7小题)
14.解:由俯视图可得最底层有4盒,由正视图和左视图可得第二层有2盒,第三层有1盒,共有7盒,
故答案为:7.
15.解:根据题意得:
,
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为:7.
16.解:根据三视图得圆锥的母线长为8,底面圆的半径为10÷2=5,
所以圆锥的侧面积=×2π×5×8=40π,圆柱的侧面积=2π×5×6=60π,
所以每顶帐篷的表面积=40π+60π=100π.
故答案为:100π.
17.解:易得三摞碟子数从左往右分别为5,4,3,
则这个桌子上共有5+4+3=12个碟子.
故答案为:12.
18.解:∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体;最多有5个正方体,
∴该组合几何体最少有5+2=7个正方体,最多有5+5=10个正方体.
故答案为:7,10.
19.解:这个几何体的主视图有三列,从左到右分别是3,4,1,左视图有三列,从左到右分别是3,4,2,
表面积为:(8+9+6)×2=46,
故答案为:46.
20.解:根据题意,圆锥的侧面积=rl=×2×2π=2π.
故答案为:2π.
一.选择题(共13小题)
1.如图是由几个小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,则该几何体的主视图是( )
A. B. C. D.
2.如图是由若干个棱长为1的小正方体搭成的一个几何体的三视图,则这个几何体的体积是( )
A.5 B.6 C.8 D.12
3.如图,已知圆锥的三视图所示,则这个圆锥的侧面展开图扇形的圆心角的度数为( )
A.270° B.216° C.108° D.135°
4.如图,是由5个大小一样的立方体摆放而成的,移动立方体A,由图1变化至图2,那么由图1的三视图变化至图2的三视图中,则( )
A.左视图不变,俯视图不变
B.主视图不变,左视图不变
C.主视图不变,俯视图不变
D.三个视图都不变
5.如图是一个几何体的三视图,则此三视图所对应的直观图是( )
A. B. C. D.
6.某几何体的三视图及相关数据如图所示,则该几何体的侧面积是( )
A.4π B.60π C.15π D.8π
7.如图,是一个长方体的三视图,则该长方体的体积是( )
A.m3﹣3m2+2m B.m3﹣2m C.m3+m2﹣2m D.m3+m2﹣m
8.如图是由六个大小相同的小正方体搭成的几何体的俯视图,则该几何体的左视图不可能是( )
A. B.
C. D.
9.一个几何体由若干个大小相同的小正方体组成,它的俯视图和左视图如图所示,则构成这个几何体的小正方体的个数最多为( )
A.4个 B.5个 C.6个 D.7个
10.如图是由若干个棱长为2的小正方体搭成的物体的三个视图,则这个物体的体积为( )
A.48 B.56 C.64 D.72
11.如图,是一个正六棱柱的主视图和左视图,则图中x的值为( )
A.2 B.3 C. D.
12.如图是由一些相同的小正方体搭成的几何体从正面、左面、上面看到的形状图,则搭成这个几何体的小正方体的个数是( )
A.4 B.5 C.6 D.7
13.由6个大小相同的正方体搭成的几何体如图所示,比较从三个不同方向看到的平面图形的面积,则( )
A.从三个不同方向看到的平面图形的面积一样大
B.从正面看到的平面图形面积最小
C.从左面看到的平面图形的面积最小
D.从上面看到的平面图形的面积最小
二.填空题(共7小题)
14.小颖同学到学校领来n盒粉笔,整齐地摞在讲桌上,从三面看到的平面图形如图所示,则n的值是 .
15.根据几何体的主视图和俯视图,搭成该几何体的小正方体最多 个.
16.如图是一个无底帐篷的三视图,该帐篷的表面积是 (结果保留π).
17.在一张桌子上摆放着一些碟子,从3个方向看到的3种视图如图所示,则这个桌子上的碟子共有 个.
18.用若干个大小相同的小立方块搭一个几何体,使得从正面和从上面看到的这个几何体的形状如图所示,则搭出这个几何体至少需要 个小立方体,最多需要 个小立方体.
19.如图,是由几个边长为1的小立方体所组成的几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,则这个几何体的表面积为 .
20.如图放置的一个圆锥,它的主视图是边长为2的等边三角形,则该圆锥的侧面积为 (结果保留π)
参考答案
一.选择题(共13小题)
1.解:观察图形可知,该几何体的主视图是.
故选:A.
2.解:综合三视图,我们可以得出,这个几何模型的底层有3+1=5个小正方体,第二层有1个小正方体,
因此搭成这个几何体模型所用的小正方体的个数是5+1=6个.
∴这个几何体的体积是6×13=6,
故选:B.
3.解:观察三视图得:圆锥的底面半径为3cm,高为4cm,
所以圆锥的母线长为5cm,
=6π,解得n=216°.
故选:B.
4.解:主视图都是第一层三个正方形,第二层右边一个正方形,故主视图不变;
左视图都是第一层两个正方形,正方形位置发生了变化,故左视图改变;
俯视图底层的正方形没有变化,故俯视图不变.
∴主视图不变,俯视图不变.
故选:C.
5.解:由图可得,此三视图所对应的直观图是.
故选:B.
6.解:观察图形可知:
圆锥母线长为:=2,
所以圆锥侧面积为:πrl=2×2×π=4π.
故选:A.
7.解:观察三视图发现该长方体的长、宽、高分别为m+2、m、m﹣1,
依题意可求出该几何体的体积为(m+2)?m?(m﹣1)=m3+m2﹣2m.
故选:C.
8.解:根据俯视图可得,左视图有三列,第2层只能有一个,
故选:B.
9.解:由俯视图与左视图知,该几何体所需小正方体个数最多分布情况如下图所示:
故选:D.
10.解:由三视图可知,物体由8个小正方体堆积而成,其中第一排最右边有一个正方体,第二排最左边有一个正方体,中间有两个正方体上下堆积,第三排中间有一个正方体,最右边有一个正方体,
右图为该物体的俯视图,每个正方体里面的数字为该位置小正方体的个数,一共有8个小正方体,每个棱长为2,故每个小正方体的体积为2×2×2=8.
故该物体的体积为:8×8=64.
故选:C.
11.解:正六棱柱的底面如图所示,过点A作AH⊥BC于H.
由题意得,2AH+BD=6,
∵∠BAC=120°,AC=AB,
∴∠CAH=∠BAH=60°,
∴∠ABH=30°,
∴AB=2AH,
∴4AH=6,
∴AH=,
∴BH=AH=,
∴x的值为,
故选:D.
12.解:从主视图和俯视图可知,几何体的底层有3个正方体,
从主视图和左视图可知,几何体的第二层有2个正方体,
则搭成这个几何体的小正方体的个数为:3+2=5,
故选:B.
13.解:主视图有5个小正方形,左视图有3个小正方形,俯视图有4个小正方形,
从左面看图形面积最小.
故选:C.
二.填空题(共7小题)
14.解:由俯视图可得最底层有4盒,由正视图和左视图可得第二层有2盒,第三层有1盒,共有7盒,
故答案为:7.
15.解:根据题意得:
,
则搭成该几何体的小正方体最多是1+1+1+2+2=7(个).
故答案为:7.
16.解:根据三视图得圆锥的母线长为8,底面圆的半径为10÷2=5,
所以圆锥的侧面积=×2π×5×8=40π,圆柱的侧面积=2π×5×6=60π,
所以每顶帐篷的表面积=40π+60π=100π.
故答案为:100π.
17.解:易得三摞碟子数从左往右分别为5,4,3,
则这个桌子上共有5+4+3=12个碟子.
故答案为:12.
18.解:∵俯视图有5个正方形,
∴最底层有5个正方体,
由主视图可得第2层最少有2个正方体;最多有5个正方体,
∴该组合几何体最少有5+2=7个正方体,最多有5+5=10个正方体.
故答案为:7,10.
19.解:这个几何体的主视图有三列,从左到右分别是3,4,1,左视图有三列,从左到右分别是3,4,2,
表面积为:(8+9+6)×2=46,
故答案为:46.
20.解:根据题意,圆锥的侧面积=rl=×2×2π=2π.
故答案为:2π.
