11.3 多边形的内角与外角 课件(共38张PPT)
文档属性
| 名称 | 11.3 多边形的内角与外角 课件(共38张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 08:13:18 | ||
图片预览



文档简介
(共38张PPT)
11.1
多边形的内角与外角
第十一章
三角形
人教版
八年级上
新知导入
板块一:多边形相关概念
新知导入
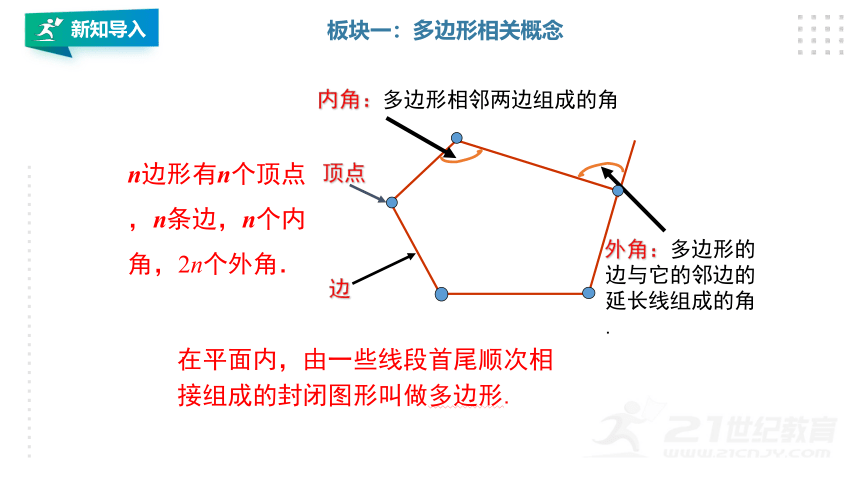
内角:多边形相邻两边组成的角
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
板块一:多边形相关概念
新知导入
板块一:多边形相关概念
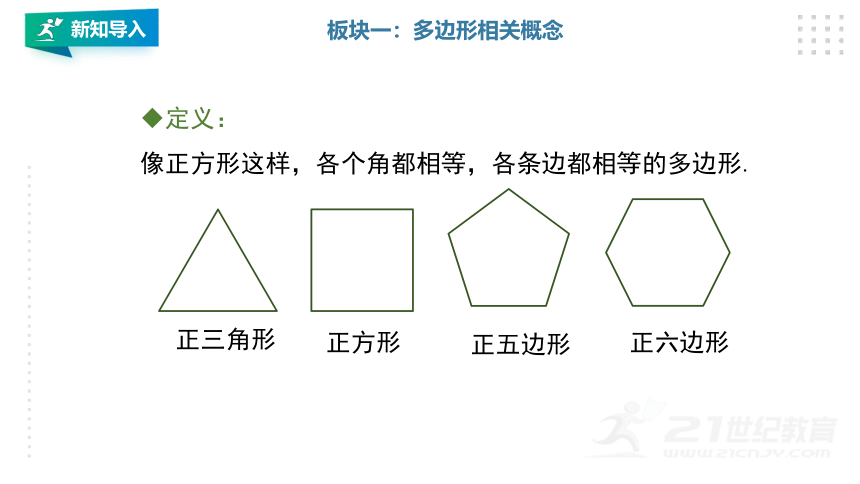
定义:
像正方形这样,各个角都相等,各条边都相等的多边形.
正三角形
正方形
正五边形
正六边形
新知导入
板块一:多边形的内角和
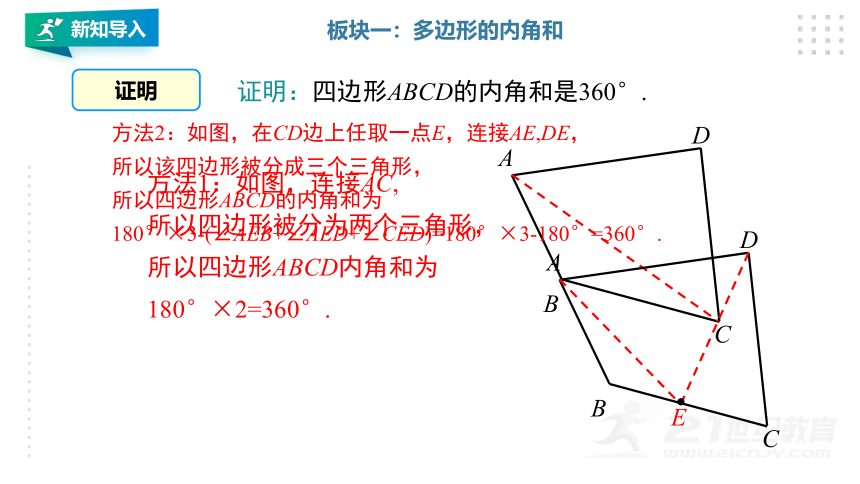
证明:四边形ABCD的内角和是360°.
证明
方法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
A
B
C
D
E
方法2:如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
新知导入
板块一:多边形的内角和
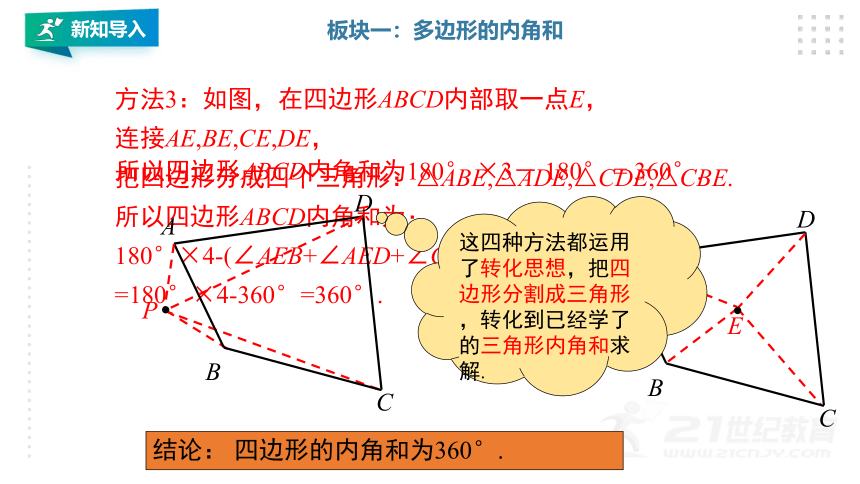
方法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
A
B
C
D
P
所以四边形ABCD内角和为180°
×3-
180°
=
360°.
这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
结论:
四边形的内角和为360°.
新知讲解
三角形
六边形
四边形
八边形
……
五边形
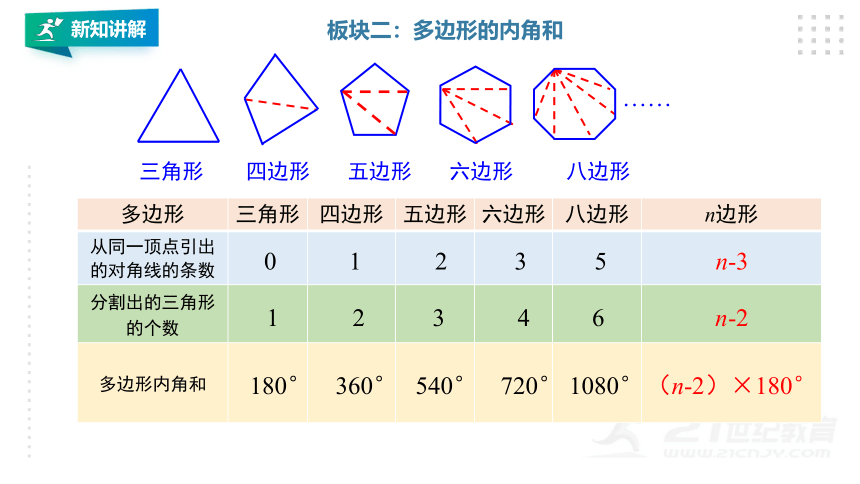
多边形
三角形
四边形
五边形
六边形
八边形
n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
多边形内角和
0
1
2
3
5
n-3
1
2
3
4
6
n-2
180°
360°
540°
720°
1080°
(n-2)×180°
板块二:多边形的内角和
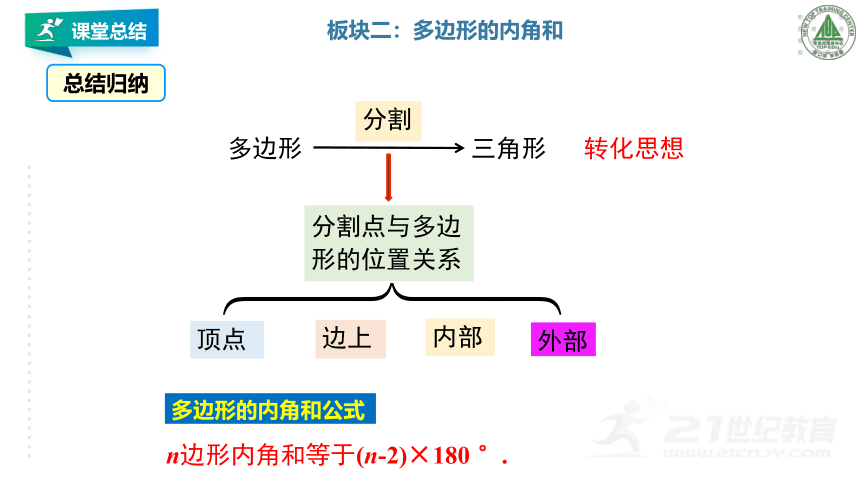
课堂总结
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180
°.
板块二:多边形的内角和
新知导入
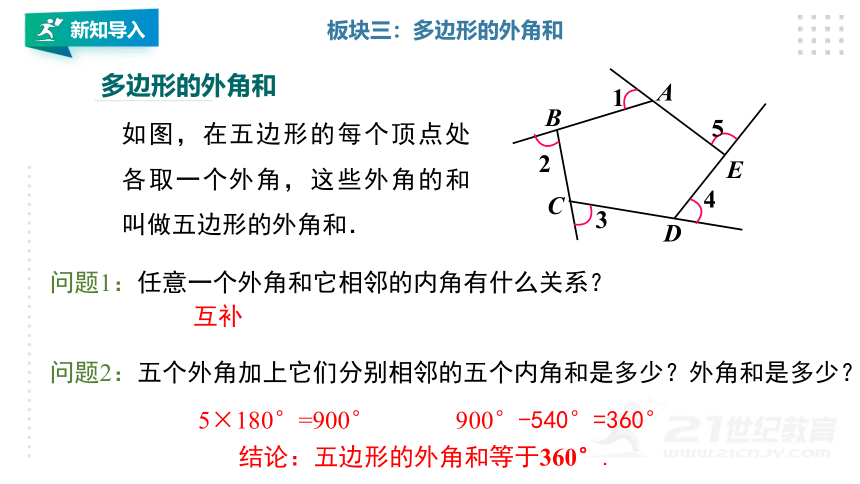
多边形的外角和
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?外角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°=900°
结论:五边形的外角和等于360°.
900°-540°=360°
板块三:多边形的外角和
板书设计
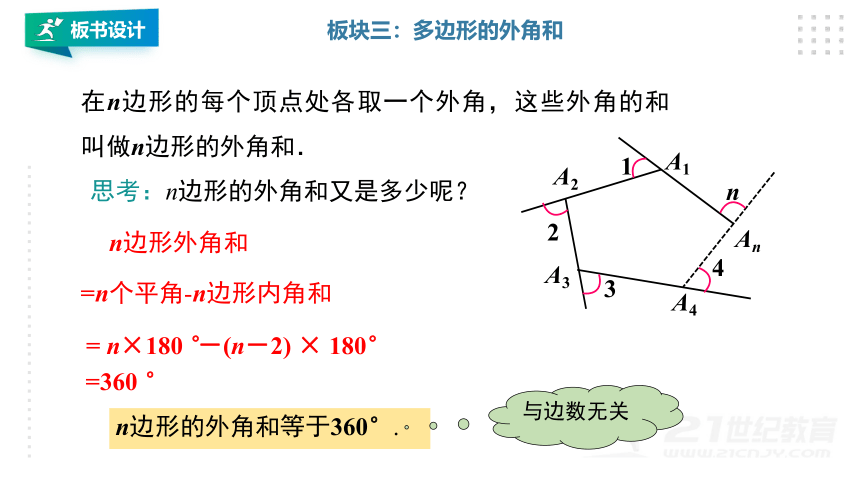
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2)
×
180°
=360
°
=n个平角-n边形内角和
=
n×180
°
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
与边数无关
板块三:多边形的外角和
新知总结
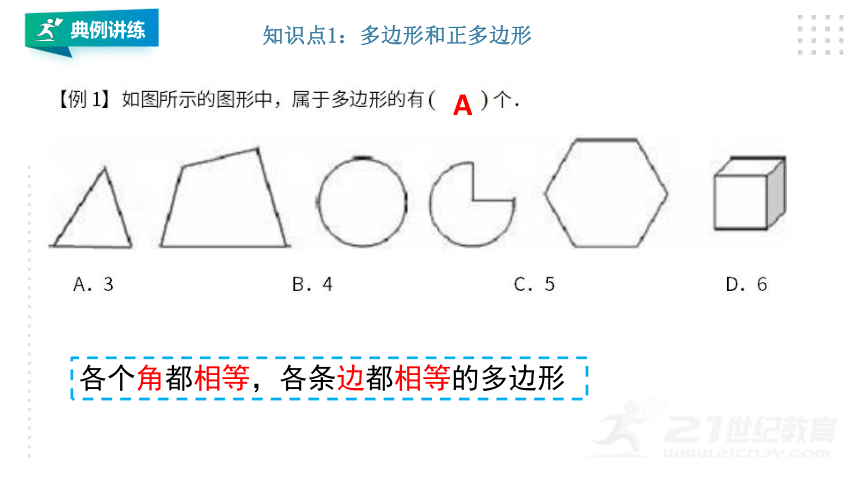
典例讲练
知识点1:多边形和正多边形
A
各个角都相等,各条边都相等的多边形
典例讲练
知识点1:多边形和正多边形
D
典例讲练
知识点1:多边形和正多边形
正方形
典例讲练
知识点2:多边形的内角和相关问题
6
C
多边形的边n=内角和÷180°+2
典例讲练
知识点2:多边形的内角和相关问题
四边形的内角和等于360°
A
典例讲练
知识点3:多边形的外角和相关问题
D
任意多边形的外角和等于360°
典例讲练
知识点3:多边形的外角和相关问题
任意多边形的外角和等于360°
360°
典例讲练
知识点3:多边形的外角和相关问题
四边形的内角和等于360°
40°
典例讲练
知识点4:根据多边形的内角和与外角和综合解题
典例讲练
知识点4:根据多边形的内角和与外角和综合解题
能力提升
题型1:多边形内角和与外角和的实际应用
能力提升
D
解答:360°÷5=72°
能力提升
能力提升
题型2:多边形与求多角和问题
答案:360°
提示:两个三角形的内角和
能力提升
A
能力提升
2
1
3
能力提升
题型3:多边形与求阴影面积问题
能力提升
题型4:多边形的对角线与边数问题
B
能力提升
9
多变形从一个顶点引对角线的条数是(n-3)条
能力提升
(n-3)
能力提升
能力提升
题型5:多边形的角与最多最少问题
能力提升
A
方法:内角是360的因数
能力提升
C
新知总结
https://www.21cnjy.com/help/help_extract.php
11.1
多边形的内角与外角
第十一章
三角形
人教版
八年级上
新知导入
板块一:多边形相关概念
新知导入
内角:多边形相邻两边组成的角
顶点
边
外角:多边形的边与它的邻边的延长线组成的角.
n边形有n个顶点,n条边,n个内角,2n个外角.
在平面内,由一些线段首尾顺次相接组成的封闭图形叫做多边形.
板块一:多边形相关概念
新知导入
板块一:多边形相关概念
定义:
像正方形这样,各个角都相等,各条边都相等的多边形.
正三角形
正方形
正五边形
正六边形
新知导入
板块一:多边形的内角和
证明:四边形ABCD的内角和是360°.
证明
方法1:如图,连接AC,
所以四边形被分为两个三角形,
所以四边形ABCD内角和为
180°×2=360°.
A
B
C
D
A
B
C
D
E
方法2:如图,在CD边上任取一点E,连接AE,DE,
所以该四边形被分成三个三角形,
所以四边形ABCD的内角和为
180°×3-(∠AEB+∠AED+∠CED)=180°×3-180°=360°.
新知导入
板块一:多边形的内角和
方法3:如图,在四边形ABCD内部取一点E,
连接AE,BE,CE,DE,
把四边形分成四个三角形:△ABE,△ADE,△CDE,△CBE.
所以四边形ABCD内角和为:
180°×4-(∠AEB+∠AED+∠CED+∠CEB)
=180°×4-360°=360°.
A
B
C
D
E
A
B
C
D
P
所以四边形ABCD内角和为180°
×3-
180°
=
360°.
这四种方法都运用了转化思想,把四边形分割成三角形,转化到已经学了的三角形内角和求解.
结论:
四边形的内角和为360°.
新知讲解
三角形
六边形
四边形
八边形
……
五边形
多边形
三角形
四边形
五边形
六边形
八边形
n边形
从同一顶点引出的对角线的条数
分割出的三角形的个数
多边形内角和
0
1
2
3
5
n-3
1
2
3
4
6
n-2
180°
360°
540°
720°
1080°
(n-2)×180°
板块二:多边形的内角和
课堂总结
分割
多边形
三角形
分割点与多边形的位置关系
顶点
边上
内部
外部
转化思想
总结归纳
多边形的内角和公式
n边形内角和等于(n-2)×180
°.
板块二:多边形的内角和
新知导入
多边形的外角和
如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.
问题1:任意一个外角和它相邻的内角有什么关系?
问题2:五个外角加上它们分别相邻的五个内角和是多少?外角和是多少?
E
B
C
D
1
2
3
4
5
A
互补
5×180°=900°
结论:五边形的外角和等于360°.
900°-540°=360°
板块三:多边形的外角和
板书设计
在n边形的每个顶点处各取一个外角,这些外角的和叫做n边形的外角和.
n边形外角和
n边形的外角和等于360°.
-(n-2)
×
180°
=360
°
=n个平角-n边形内角和
=
n×180
°
An
A2
A3
A4
1
2
3
4
n
A1
思考:n边形的外角和又是多少呢?
与边数无关
板块三:多边形的外角和
新知总结
典例讲练
知识点1:多边形和正多边形
A
各个角都相等,各条边都相等的多边形
典例讲练
知识点1:多边形和正多边形
D
典例讲练
知识点1:多边形和正多边形
正方形
典例讲练
知识点2:多边形的内角和相关问题
6
C
多边形的边n=内角和÷180°+2
典例讲练
知识点2:多边形的内角和相关问题
四边形的内角和等于360°
A
典例讲练
知识点3:多边形的外角和相关问题
D
任意多边形的外角和等于360°
典例讲练
知识点3:多边形的外角和相关问题
任意多边形的外角和等于360°
360°
典例讲练
知识点3:多边形的外角和相关问题
四边形的内角和等于360°
40°
典例讲练
知识点4:根据多边形的内角和与外角和综合解题
典例讲练
知识点4:根据多边形的内角和与外角和综合解题
能力提升
题型1:多边形内角和与外角和的实际应用
能力提升
D
解答:360°÷5=72°
能力提升
能力提升
题型2:多边形与求多角和问题
答案:360°
提示:两个三角形的内角和
能力提升
A
能力提升
2
1
3
能力提升
题型3:多边形与求阴影面积问题
能力提升
题型4:多边形的对角线与边数问题
B
能力提升
9
多变形从一个顶点引对角线的条数是(n-3)条
能力提升
(n-3)
能力提升
能力提升
题型5:多边形的角与最多最少问题
能力提升
A
方法:内角是360的因数
能力提升
C
新知总结
https://www.21cnjy.com/help/help_extract.php
