北师大版2021年暑假广东省揭阳市梦飞培训机构七年级上册数学第一章 丰富的图形世界单元检测卷(Word版含解析)
文档属性
| 名称 | 北师大版2021年暑假广东省揭阳市梦飞培训机构七年级上册数学第一章 丰富的图形世界单元检测卷(Word版含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 238.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-04 00:00:00 | ||
图片预览


文档简介
2021年暑假广东省揭阳市梦飞培训机构七年级上册数学第一章 丰富的图形世界单元检测卷
一、选择题
1.在下图的四个立体图形中,从正面看是四边形的立体图形有(? )
A.?1个?????????????????????B.?2个?????????????????C.?3个?????????????D.?4个
2.将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是(?? )
A.???B.???C.???D.?
3.把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是(?? )
A.?五棱锥?????????B.?五棱柱????????????????C.?六棱锥?????????????D.?六棱柱
4.用一平面截一个正方体,不能得到的截面形状是( )
A.?等边三角形??????????????????B.?长方形?????????????????C.?六边形?????????????????D.?七边形
5.如图所示的几何体的从上面看到的形状图是(?? )
A.????B.????????C.???????D.?
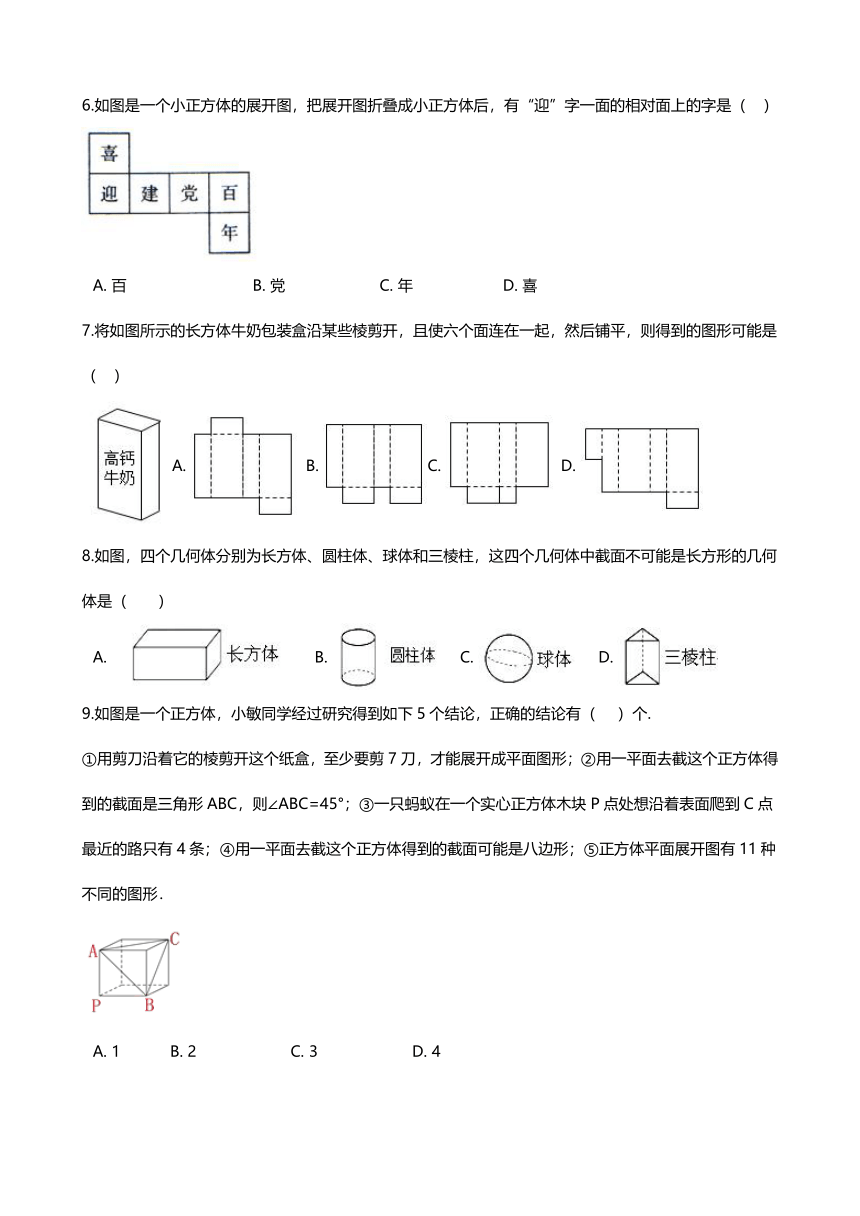
6.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“迎”字一面的相对面上的字是(?? )
A.?百????????????????????????????B.?党?????????????????????C.?年????????????????????D.?喜
7.将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形可能是( ??)
A.??B.?C.??D.?
8.如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中截面不可能是长方形的几何体是( )
A.?? ??????B.??????C.?????D.?
9.如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有(??? )个.
①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
A.?1???????????B.?2?????????????????????C.?3?????????????????????D.?4
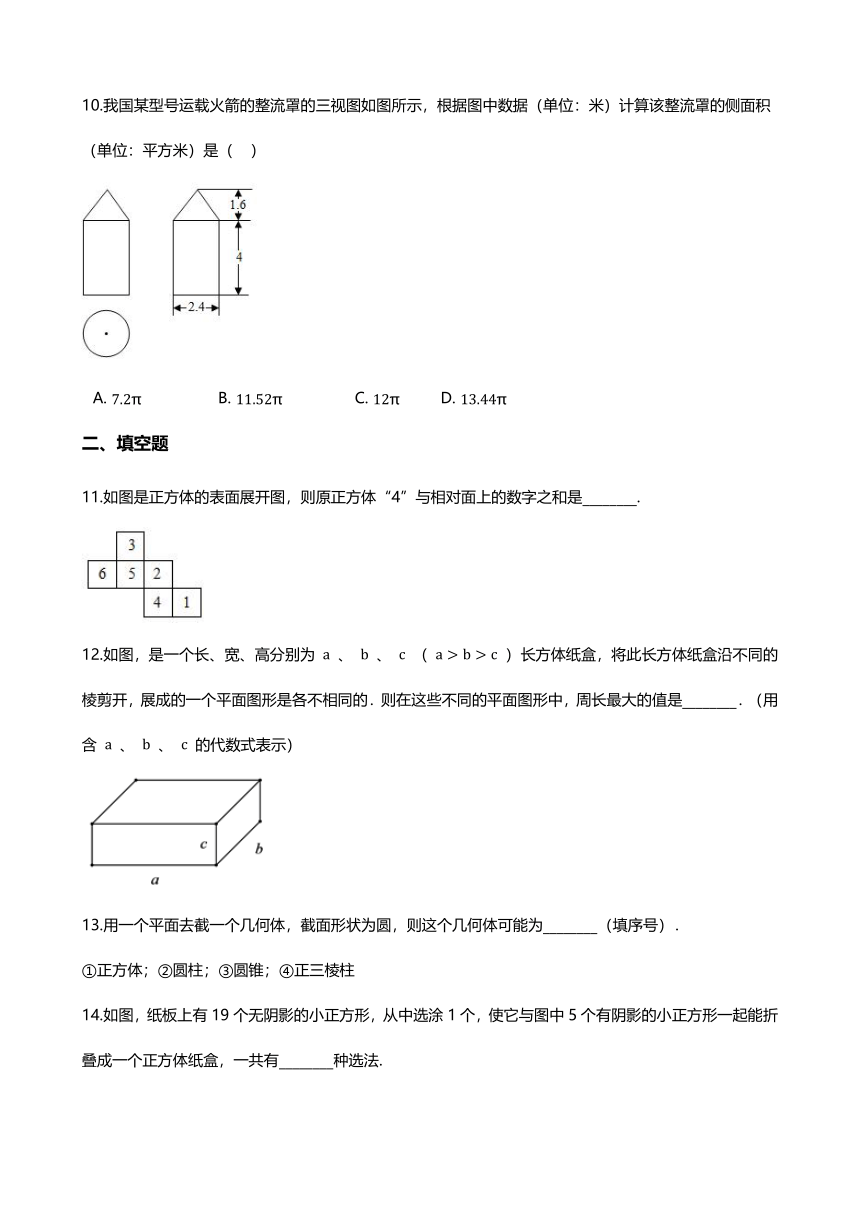
10.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是(?? )
A.?7.2π?????????????????B.?11.52π????????????????C.?12π?????????D.?13.44π
二、填空题
11.如图是正方体的表面展开图,则原正方体“4”与相对面上的数字之和是________.
12.如图,是一个长、宽、高分别为 a 、 b 、 c ( a>b>c )长方体纸盒,将此长方体纸盒沿不同的棱剪开,展成的一个平面图形是各不相同的.则在这些不同的平面图形中,周长最大的值是________.(用含 a 、 b 、 c 的代数式表示)
13.用一个平面去截一个几何体,截面形状为圆,则这个几何体可能为________(填序号).
①正方体;②圆柱;③圆锥;④正三棱柱
14.如图,纸板上有19个无阴影的小正方形,从中选涂1个,使它与图中5个有阴影的小正方形一起能折叠成一个正方体纸盒,一共有________种选法.
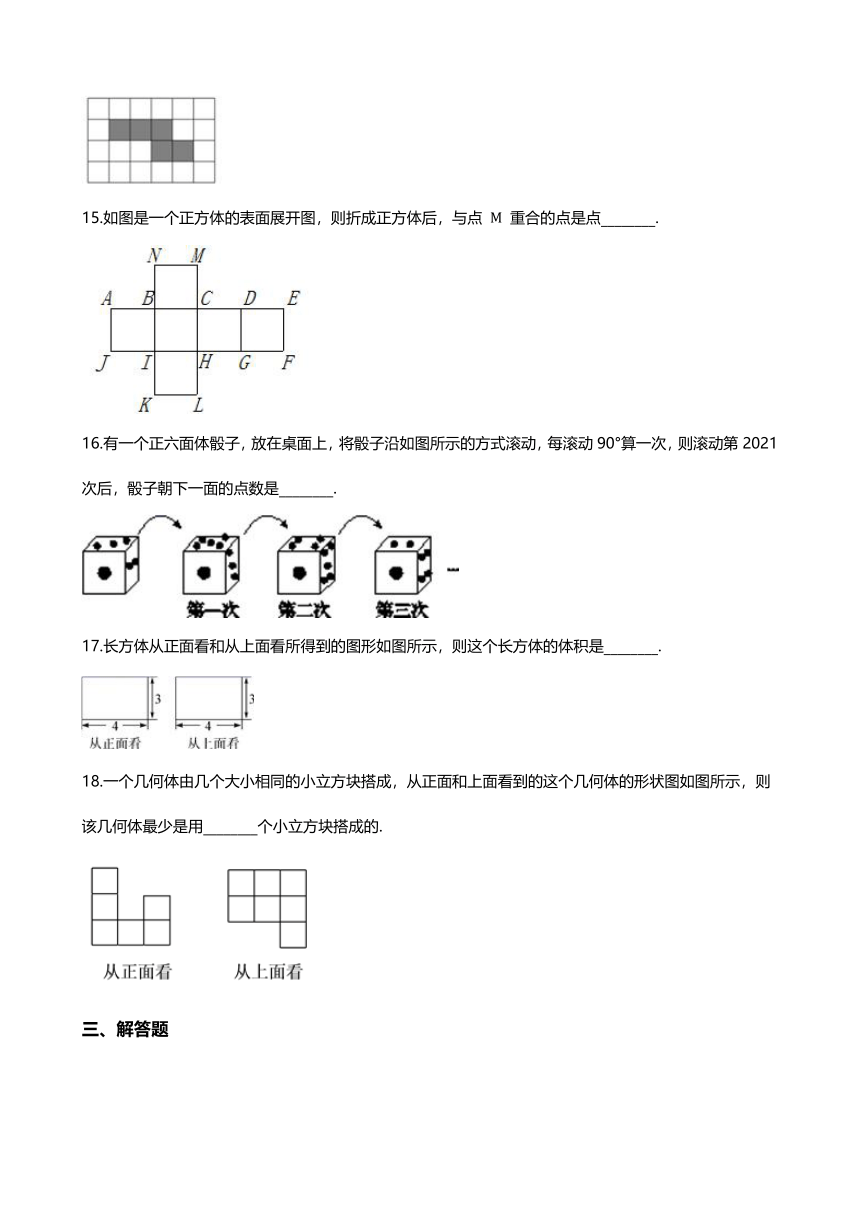
15.如图是一个正方体的表面展开图,则折成正方体后,与点 M 重合的点是点________.
16.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的方式滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是________.
17.长方体从正面看和从上面看所得到的图形如图所示,则这个长方体的体积是________.
18.一个几何体由几个大小相同的小立方块搭成,从正面和上面看到的这个几何体的形状图如图所示,则该几何体最少是用________个小立方块搭成的.
三、解答题
19.小名准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,你能在图中的拼接图形上再接一个正方形画出阴影,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子吗?请在下面的图①和图②中画出两种不同的补充方法.
20.我们知道,将一个长方形绕它的一边旋转一周得到的几何体是圆柱,现有一个长是5cm,宽是3cm的长方形,分别绕它的长和宽所在的直线旋转一周,得到不同的圆柱几何体,分别求出它们的体积.
21.一个几何体由几个大小相同的小立方块搭成,从上面看这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面,左侧面看到的几何体的形状图.
22.下图是长方体的表面展开图,将它折叠成一个长方体.
?
(1)哪几个点与点 N 重合?
(2)若 AE=CM=12cm , LE=2cm , KL=4cm ,求这个长方体的表面积和体积.
23.在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.下图是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30cm、宽20cm、高18cm,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.
步骤1:在符合尺寸规格的硬纸板上,画出这个长方体的展开图(草图).注意,要预留出黏合处,并适当剪去棱角.
步骤2:在你上面画出的展开草图上,标出对应的A、B、C、D的位置,标出长30cm、宽20cm、高18CM所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:裁下展开图,折叠并粘好黏合处,得到长方体包装盒.
24.如图,是由一些相同的小正方体搭成的几何体从上面看得到的形状图,小正方形中的数字表示该位置的小正方体的个数.
(1)请在方格中画出从正面看、从左面看得到的几何体的形状图;
(2)若在这个几何体上再添加一些相同的小正方体,并保持这个几何体从正面看和从上面看得到的图形不变,那么最多可以再添加________个小正方体.
25.我们知道,将一个正方体或长方体的表面沿某些棱剪开,可以展成一个平面图形.
(1)下列图形中,是正方体的表面展开图的是________.
(2)如图所示的长方体,长、宽、高分别为4、3、6,若将它的表面沿某些棱剪开,展成一个平面图形.则下列图形中,可能是该长方体表面展开图的有________(填序号)
(3)下列图是题(2)中长方体的一种表面展开图,它的外围周长为52,事实上,题(2)中长方体的表面展开图还有不少,聪明的你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.
26.如图1所示,从大正方体中截去一个小正方体之后,可以得到图2的几何体.
(1)设原大正方体的表面积为a,图2中几何体的表面积为b,那么a与b的大小关系是???????? ;
A.a>b;
B.a<b;
C.a=b;
D.无法判断.
(2)小明说“设图1中大正方体的棱长之和为m,图2中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图3是图2几何体的表面展开图吗?如有错误,请予修正.
答案
一、选择题
1.解:正方体的主视图是四边形;
球的主视图是圆;
圆柱的主视图是四边形;
圆锥的主视图是等腰三角形;
从正面看是四边形的立体图形有两个.
故答案为:B.
2.解:图中棱柱展开后,两个三角形的面不可能位于同一侧,因此D选项中的图不是它的表面展开图;
故答案为:D.
3.解:由图可知:折叠后,该几何体的底面是五边形,
则该几何体为五棱锥,
故答案为:A.
4.解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴最多可以截出六边形,
∴不可能截得七边形.
故答案为:D.
5.如图所示的几何体的从上面看到的形状图是 .
故答案为:D.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方体,“迎”与“党”是相对面,“建”与“百”是相对面,“喜”与“年”是相对面.
故答案为:B.
7.解:根据题意可知只有A符合题意.
故答案为:A.
8.解:圆柱体、长方体、三棱柱的截面都可能出现长方形,只有球体的截面只与圆有关.
故答案为:C.
9.解:(1)AB、BC、AC均是相同正方形的对角线,故AB=BC=AC,△ABC是等边三角形,∠ABC=60°,②不符合题意;(2)用一平面去截n棱柱,截面最多是(n+2)边形,正方体是四棱柱,所以截面最多是六边形,④不符合题意;(3)正方体的展开图只有11种,⑤符合题意;(4)正方体的11种展开图,六个小正方形均是一连一关系,即必须是5条边相连,正方体有12条棱,所以要剪12-5=7条棱,才能把正方体展开成平面图形,①符合题意;(5)正方体有六个面,P点属于“前、左、下面”这三个面,所以从P到C,可以走“前+上、前+右、左+上、左+后、下+右、下+后”这六处组合的面,这其中任何一个组合的两个面展开均是相同的长方形,而P到C的最短路线是这个长方形的对角线,这些对角线均相等,故从P到C的最短路线有6条;③不符合题意.
综上所述,正确的选项是①⑤,
故答案为:B
10.由图可知,运载火箭的上半部分为圆锥,底面圆的半径r为 2.4÷2=1.2 ,高为1.6.下半部分为圆柱,底面圆的半径r=1.2,高为4.
圆柱的侧面积为: S1=2πr?4=2π?1.2×4=9.6π ,
圆锥的侧面积为: S2=12lR=12×2π?1.2×(1.62+1.22)=2.4π ,
该整流罩的侧面积: S=S1+S2=9.6π+2.4π=12π .
故答案为:C.
二、填空题
11.解:∵正方体的展开图,原正方体“4”的相对面上的数字为3,
∴原正方体“4”与相对面上的数字之和是7.
故答案为:7.
12.解:如图,此平面图形就是长方体展开时周长最大的图形,最大周长为8a+4b+2c,
故答案为:8a+4b+2c.
13.解:①正方体截面形状不可能是圆,不符合题意;
②圆柱截面形状可能是圆,符合题意;
③圆锥截面形状可能是圆,符合题意;
④正三棱柱截面形状不可能是圆,不符合题意.
故答案为:②③.
14.解:如图所示:共4种.
故答案为:4.
15.先从拐角C处研究,CM与CD重合, DE与MN重合,DG过顶点M,从而点M与点D重合,一个点属于三个面,而点M已经属于面MNBC,面EFGD,面DCHG,因此没有其它点与点M重合.
故答案为:D.
16.解:观察图形知道:
第一次点数五和点二数相对,
第二次点数四和点数三相对,
第三次点数二和点数五相对,
第四次点数三和点数四相对,
第五次点数五和点二数相对,
且四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第一次相同,
∴朝下的数字是5的对面2,
故答案为:2.
17.解:由图可知,这个长方体的长为4,宽为3,高为3,∴长方体的体积V=4×3×3=36,故答案为36.
18.从上面看,可以确定是5个,从正面看,可以确定,左面有两层,至少有一个方块,所以是6个.
故答案为6个
三、解答题
19. 解:如图所示:
新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
20.解:分两种情况:①绕长所在的直线旋转一周得到圆柱体积为:π×32×5=45π(cm3);②绕宽所在的直线旋转一周得到圆柱体积为:π×52×3=75π(cm3).故它们的体积分别为45πcm3或75πcm3 .
21.如图所示:
22.(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 AE=CM=12cm , KL=4cm ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
23.步骤一:如下图(有多种作图方案,画出一种合理的即可):
步骤2:在图中标出对应的A、B、C、D的位置,标出长30cm、宽20cm、高18cm所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:按图中所示裁下展开图,折叠并粘好黏合处,即可得到长方体包装盒.
24. (1)解:从正面看、从左面看得到的几何体的形状图如图所示:
(2)3
解:(2)由不改变俯视图,所以添加的位置只能在已有正方体的上面添加,
由不改变主视图,所以添加的位置不能添加在正方体个数最多的上面,
所以添加的正方体应按如下图的方式添加,
所以最多可以再添加3个小正方体.
故答案为:3.
25. (1)B
(2)①②③
(3)解:外围周长最大的表面展开图,如图:
观察展开图可知,外围周长为6×8+4×4+3×2=48+16+6=70.
(1)A折叠后不可以组成正方体;
B折叠后可以组成正方体;
C都是“2-4”结构,出现重叠现象,不能折成正方体,即不是正方体的表面展开图,故不符合题意;
D折叠后不可以组成正方体;
故答案为:B;(2)可能是该长方体表面展开图的有①②③.
故答案为:①②③;
26. (1)C
(2)解:如图④红颜色的棱是多出来的,共6条,当且仅当每一条棱都等于原来正方体的棱长的一半,n比m正好多出大正方体的3条棱的长度,故小明的说法是不正确的;
图④
(3)解:图③不是图②几何体的表面展开图,改后的图形,如图⑤所示.
图⑤
解:(1)根据“切去三个小面”但又“新增三个相同的小面”,因此与原来的表面积相等,即a=b
故答案为:a=b;
一、选择题
1.在下图的四个立体图形中,从正面看是四边形的立体图形有(? )
A.?1个?????????????????????B.?2个?????????????????C.?3个?????????????D.?4个
2.将如图所示的直棱柱展开,下列各示意图中不可能是它的表面展开图的是(?? )
A.???B.???C.???D.?
3.把图中的纸片沿虚线折叠,可以围成一个几何体,这个几何体的名称是(?? )
A.?五棱锥?????????B.?五棱柱????????????????C.?六棱锥?????????????D.?六棱柱
4.用一平面截一个正方体,不能得到的截面形状是( )
A.?等边三角形??????????????????B.?长方形?????????????????C.?六边形?????????????????D.?七边形
5.如图所示的几何体的从上面看到的形状图是(?? )
A.????B.????????C.???????D.?
6.如图是一个小正方体的展开图,把展开图折叠成小正方体后,有“迎”字一面的相对面上的字是(?? )
A.?百????????????????????????????B.?党?????????????????????C.?年????????????????????D.?喜
7.将如图所示的长方体牛奶包装盒沿某些棱剪开,且使六个面连在一起,然后铺平,则得到的图形可能是( ??)
A.??B.?C.??D.?
8.如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中截面不可能是长方形的几何体是( )
A.?? ??????B.??????C.?????D.?
9.如图是一个正方体,小敏同学经过研究得到如下5个结论,正确的结论有(??? )个.
①用剪刀沿着它的棱剪开这个纸盒,至少要剪7刀,才能展开成平面图形;②用一平面去截这个正方体得到的截面是三角形ABC,则∠ABC=45°;③一只蚂蚁在一个实心正方体木块P点处想沿着表面爬到C点最近的路只有4条;④用一平面去截这个正方体得到的截面可能是八边形;⑤正方体平面展开图有11种不同的图形.
A.?1???????????B.?2?????????????????????C.?3?????????????????????D.?4
10.我国某型号运载火箭的整流罩的三视图如图所示,根据图中数据(单位:米)计算该整流罩的侧面积(单位:平方米)是(?? )
A.?7.2π?????????????????B.?11.52π????????????????C.?12π?????????D.?13.44π
二、填空题
11.如图是正方体的表面展开图,则原正方体“4”与相对面上的数字之和是________.
12.如图,是一个长、宽、高分别为 a 、 b 、 c ( a>b>c )长方体纸盒,将此长方体纸盒沿不同的棱剪开,展成的一个平面图形是各不相同的.则在这些不同的平面图形中,周长最大的值是________.(用含 a 、 b 、 c 的代数式表示)
13.用一个平面去截一个几何体,截面形状为圆,则这个几何体可能为________(填序号).
①正方体;②圆柱;③圆锥;④正三棱柱
14.如图,纸板上有19个无阴影的小正方形,从中选涂1个,使它与图中5个有阴影的小正方形一起能折叠成一个正方体纸盒,一共有________种选法.
15.如图是一个正方体的表面展开图,则折成正方体后,与点 M 重合的点是点________.
16.有一个正六面体骰子,放在桌面上,将骰子沿如图所示的方式滚动,每滚动90°算一次,则滚动第2021次后,骰子朝下一面的点数是________.
17.长方体从正面看和从上面看所得到的图形如图所示,则这个长方体的体积是________.
18.一个几何体由几个大小相同的小立方块搭成,从正面和上面看到的这个几何体的形状图如图所示,则该几何体最少是用________个小立方块搭成的.
三、解答题
19.小名准备制作一个封闭的正方体盒子,他先用5个大小一样的正方形制成如图所示的拼接图形(实线部分),经折叠后发现还少一个面,你能在图中的拼接图形上再接一个正方形画出阴影,使新拼接成的图形经过折叠后能成为一个封闭的正方体盒子吗?请在下面的图①和图②中画出两种不同的补充方法.
20.我们知道,将一个长方形绕它的一边旋转一周得到的几何体是圆柱,现有一个长是5cm,宽是3cm的长方形,分别绕它的长和宽所在的直线旋转一周,得到不同的圆柱几何体,分别求出它们的体积.
21.一个几何体由几个大小相同的小立方块搭成,从上面看这个几何体,看到的形状如图所示,其中小正方形中的数字表示在该位置的小立方块的个数,请画出从正面,左侧面看到的几何体的形状图.
22.下图是长方体的表面展开图,将它折叠成一个长方体.
?
(1)哪几个点与点 N 重合?
(2)若 AE=CM=12cm , LE=2cm , KL=4cm ,求这个长方体的表面积和体积.
23.在我们的课本第142页“4.4课题学习”中,有包装纸盒的设计制作方法.下图是设计师为“XX快递”设计的长方体包装盒的轮廓草图,其中长30cm、宽20cm、高18cm,正面有“快递”字样,上面有“上”字样,棱AB是上盖的掀开处,棱CD是粘合处.请你想想,如何制作这个包装盒,然后完善下面的制作步骤.
步骤1:在符合尺寸规格的硬纸板上,画出这个长方体的展开图(草图).注意,要预留出黏合处,并适当剪去棱角.
步骤2:在你上面画出的展开草图上,标出对应的A、B、C、D的位置,标出长30cm、宽20cm、高18CM所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:裁下展开图,折叠并粘好黏合处,得到长方体包装盒.
24.如图,是由一些相同的小正方体搭成的几何体从上面看得到的形状图,小正方形中的数字表示该位置的小正方体的个数.
(1)请在方格中画出从正面看、从左面看得到的几何体的形状图;
(2)若在这个几何体上再添加一些相同的小正方体,并保持这个几何体从正面看和从上面看得到的图形不变,那么最多可以再添加________个小正方体.
25.我们知道,将一个正方体或长方体的表面沿某些棱剪开,可以展成一个平面图形.
(1)下列图形中,是正方体的表面展开图的是________.
(2)如图所示的长方体,长、宽、高分别为4、3、6,若将它的表面沿某些棱剪开,展成一个平面图形.则下列图形中,可能是该长方体表面展开图的有________(填序号)
(3)下列图是题(2)中长方体的一种表面展开图,它的外围周长为52,事实上,题(2)中长方体的表面展开图还有不少,聪明的你能画出一个使外围周长最大的表面展开图吗?请画出这个表面展开图,并求出它的外围周长.
26.如图1所示,从大正方体中截去一个小正方体之后,可以得到图2的几何体.
(1)设原大正方体的表面积为a,图2中几何体的表面积为b,那么a与b的大小关系是???????? ;
A.a>b;
B.a<b;
C.a=b;
D.无法判断.
(2)小明说“设图1中大正方体的棱长之和为m,图2中几何体的各棱长之和为n,那么n比m正好多出大正方体的3条棱的长度.”你认为小明的说法正确吗?为什么?
(3)如果截去的小正方体的棱长为大正方体的棱长的一半,那么图3是图2几何体的表面展开图吗?如有错误,请予修正.
答案
一、选择题
1.解:正方体的主视图是四边形;
球的主视图是圆;
圆柱的主视图是四边形;
圆锥的主视图是等腰三角形;
从正面看是四边形的立体图形有两个.
故答案为:B.
2.解:图中棱柱展开后,两个三角形的面不可能位于同一侧,因此D选项中的图不是它的表面展开图;
故答案为:D.
3.解:由图可知:折叠后,该几何体的底面是五边形,
则该几何体为五棱锥,
故答案为:A.
4.解:∵用平面去截正方体时最多与六个面相交得六边形,最少与三个面相交得三角形,
∴最多可以截出六边形,
∴不可能截得七边形.
故答案为:D.
5.如图所示的几何体的从上面看到的形状图是 .
故答案为:D.
6.解:正方体的表面展开图,相对的面之间一定相隔一个正方体,“迎”与“党”是相对面,“建”与“百”是相对面,“喜”与“年”是相对面.
故答案为:B.
7.解:根据题意可知只有A符合题意.
故答案为:A.
8.解:圆柱体、长方体、三棱柱的截面都可能出现长方形,只有球体的截面只与圆有关.
故答案为:C.
9.解:(1)AB、BC、AC均是相同正方形的对角线,故AB=BC=AC,△ABC是等边三角形,∠ABC=60°,②不符合题意;(2)用一平面去截n棱柱,截面最多是(n+2)边形,正方体是四棱柱,所以截面最多是六边形,④不符合题意;(3)正方体的展开图只有11种,⑤符合题意;(4)正方体的11种展开图,六个小正方形均是一连一关系,即必须是5条边相连,正方体有12条棱,所以要剪12-5=7条棱,才能把正方体展开成平面图形,①符合题意;(5)正方体有六个面,P点属于“前、左、下面”这三个面,所以从P到C,可以走“前+上、前+右、左+上、左+后、下+右、下+后”这六处组合的面,这其中任何一个组合的两个面展开均是相同的长方形,而P到C的最短路线是这个长方形的对角线,这些对角线均相等,故从P到C的最短路线有6条;③不符合题意.
综上所述,正确的选项是①⑤,
故答案为:B
10.由图可知,运载火箭的上半部分为圆锥,底面圆的半径r为 2.4÷2=1.2 ,高为1.6.下半部分为圆柱,底面圆的半径r=1.2,高为4.
圆柱的侧面积为: S1=2πr?4=2π?1.2×4=9.6π ,
圆锥的侧面积为: S2=12lR=12×2π?1.2×(1.62+1.22)=2.4π ,
该整流罩的侧面积: S=S1+S2=9.6π+2.4π=12π .
故答案为:C.
二、填空题
11.解:∵正方体的展开图,原正方体“4”的相对面上的数字为3,
∴原正方体“4”与相对面上的数字之和是7.
故答案为:7.
12.解:如图,此平面图形就是长方体展开时周长最大的图形,最大周长为8a+4b+2c,
故答案为:8a+4b+2c.
13.解:①正方体截面形状不可能是圆,不符合题意;
②圆柱截面形状可能是圆,符合题意;
③圆锥截面形状可能是圆,符合题意;
④正三棱柱截面形状不可能是圆,不符合题意.
故答案为:②③.
14.解:如图所示:共4种.
故答案为:4.
15.先从拐角C处研究,CM与CD重合, DE与MN重合,DG过顶点M,从而点M与点D重合,一个点属于三个面,而点M已经属于面MNBC,面EFGD,面DCHG,因此没有其它点与点M重合.
故答案为:D.
16.解:观察图形知道:
第一次点数五和点二数相对,
第二次点数四和点数三相对,
第三次点数二和点数五相对,
第四次点数三和点数四相对,
第五次点数五和点二数相对,
且四次一循环,
∵2021÷4=505…1,
∴滚动第2021次后与第一次相同,
∴朝下的数字是5的对面2,
故答案为:2.
17.解:由图可知,这个长方体的长为4,宽为3,高为3,∴长方体的体积V=4×3×3=36,故答案为36.
18.从上面看,可以确定是5个,从正面看,可以确定,左面有两层,至少有一个方块,所以是6个.
故答案为6个
三、解答题
19. 解:如图所示:
新拼接成的图形经过折叠后能成为一个封闭的正方体盒子.
20.解:分两种情况:①绕长所在的直线旋转一周得到圆柱体积为:π×32×5=45π(cm3);②绕宽所在的直线旋转一周得到圆柱体积为:π×52×3=75π(cm3).故它们的体积分别为45πcm3或75πcm3 .
21.如图所示:
22.(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;
(2)解:由 AE=CM=12cm , KL=4cm ,可得CH=CM-LK=12-4=8cm,
长方体的表面积;2×(8×4+2×4+2×8)=112cm2;
体积:4×8×2=64cm3.
23.步骤一:如下图(有多种作图方案,画出一种合理的即可):
步骤2:在图中标出对应的A、B、C、D的位置,标出长30cm、宽20cm、高18cm所在线段,并把“上”和“快递”标注在所在面的位置上.
步骤3:按图中所示裁下展开图,折叠并粘好黏合处,即可得到长方体包装盒.
24. (1)解:从正面看、从左面看得到的几何体的形状图如图所示:
(2)3
解:(2)由不改变俯视图,所以添加的位置只能在已有正方体的上面添加,
由不改变主视图,所以添加的位置不能添加在正方体个数最多的上面,
所以添加的正方体应按如下图的方式添加,
所以最多可以再添加3个小正方体.
故答案为:3.
25. (1)B
(2)①②③
(3)解:外围周长最大的表面展开图,如图:
观察展开图可知,外围周长为6×8+4×4+3×2=48+16+6=70.
(1)A折叠后不可以组成正方体;
B折叠后可以组成正方体;
C都是“2-4”结构,出现重叠现象,不能折成正方体,即不是正方体的表面展开图,故不符合题意;
D折叠后不可以组成正方体;
故答案为:B;(2)可能是该长方体表面展开图的有①②③.
故答案为:①②③;
26. (1)C
(2)解:如图④红颜色的棱是多出来的,共6条,当且仅当每一条棱都等于原来正方体的棱长的一半,n比m正好多出大正方体的3条棱的长度,故小明的说法是不正确的;
图④
(3)解:图③不是图②几何体的表面展开图,改后的图形,如图⑤所示.
图⑤
解:(1)根据“切去三个小面”但又“新增三个相同的小面”,因此与原来的表面积相等,即a=b
故答案为:a=b;
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
