13.3.1《等腰三角形》课时练习2021-2022学年华东师大版数学八年级上册(Word版含答案)
文档属性
| 名称 | 13.3.1《等腰三角形》课时练习2021-2022学年华东师大版数学八年级上册(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 722.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 15:19:23 | ||
图片预览


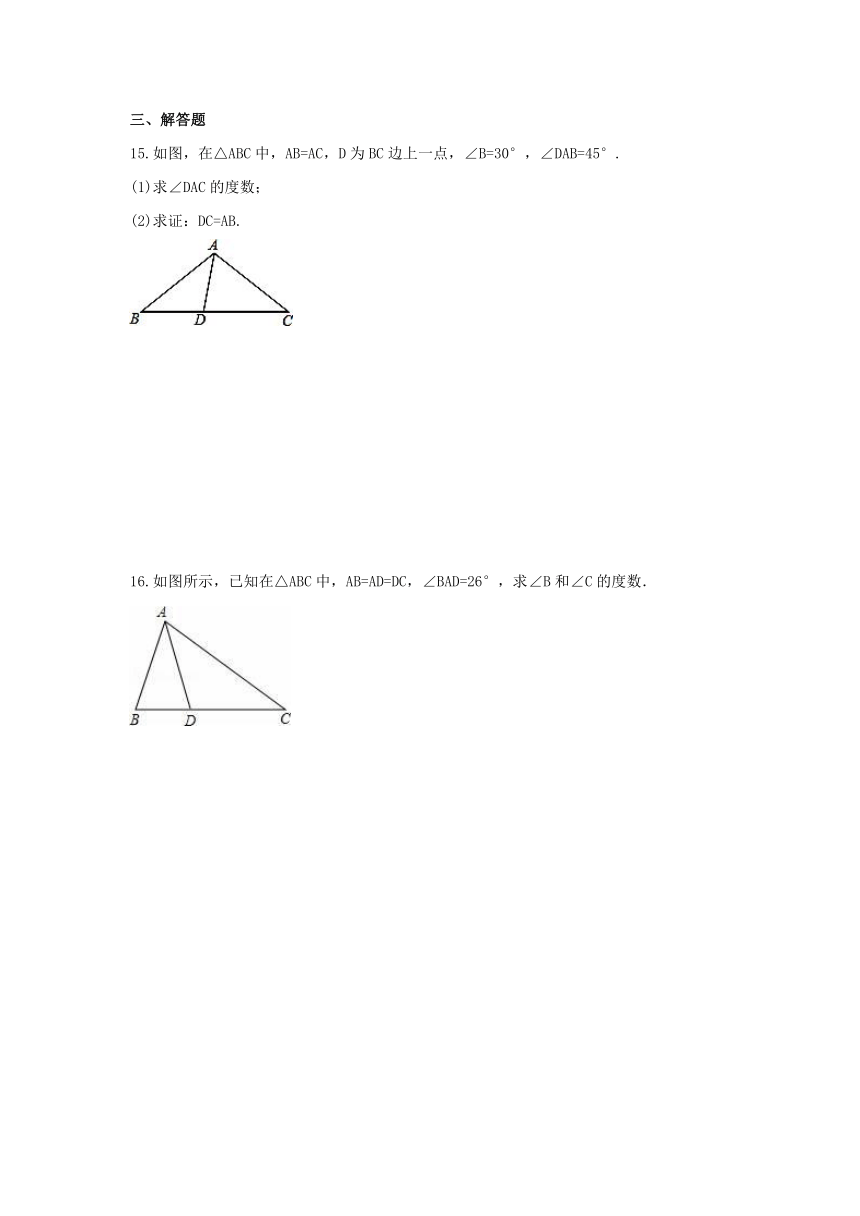
文档简介
华东师大版数学八年级上册13.3.1
《等腰三角形》课时练习
一、选择题
1.一个等腰三角形的一边长是7cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.12cm B.17cm C.19cm D.17cm或19cm
2.等腰三角形的一个角是80°,则它的底角是( )
A.50° B.80° C.50°或80° D.20°或80°
3.若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12 B.9 C.12或9 D.9或7
4.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
A.12 B.4 C.8 D.不确定
5.如果等腰三角形的一个底角为α,那么( )
A.α不大于45° B.0°<α<90° C.α不大于90° D.45°<α<90°
6.等腰三角形的一个内角为70°,则另外两个内角的度数分别是(??? )
A.55°,55°????? B.70°,40°或70°,55°
C.70°,40°??? D.55°,55°或70°,40°
7.下列关于等腰三角形的性质叙述错误的是(??? )
A.等腰三角形的两底角相等
B.等腰三角形的两边相等
C.等腰三角形是轴对称图形
D.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合
8.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
A.1个 B.3个 C.4个 D.5个
9.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.102° B.100° C.88° D.92°
10.在△ABC中,AB=AC,D、E分别在BC、AC上,AD=AE,∠CDE=20°,∠BAD度数为( )
A.36° B.40° C.45° D.50°
二、填空题
11.一个三角形等腰三角形的两边长分别为13和7,则周长为 .
12.如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F分别是AD的三等分点,若△ABC的面积为18cm2,则图中阴影部分面积为 cm2.
13.如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,
则∠DCE的大小为 (度).
14.在等腰三角形中,
(1)一腰上的高与底边的夹角为30°,则顶角为 .
(2)一腰上的高与另一腰的夹角为30°,则顶角为 .
三、解答题
15.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
16.如图所示,已知在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
17.如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
18.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,
求∠A的度数.
参考答案
1.D
2.C
3.A
4.C
5.B
6.D
7.B
8.D
9.D
10.B
11.答案为:33或27.
12.答案为:9.
13.答案为:45.
14.答案为:60°或120°.
15. (1)解:∵AB=AC,∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°,∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;
(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,∴DC=AC,∴DC=AB.
16.解:在△ABC中,AB=AD=DC,
∵AB=AD,在三角形ABD中,∠B=∠ADB=(180°﹣26°)×=77°,
又∵AD=DC,在三角形ADC中,
∴∠C==77°×=38.5°.
17.证明:(1)∵AB=AC,D是BC的中点,
∴∠BAE=∠EAC,
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)∵∠BAC=45°,BF⊥AF,
∴△ABF为等腰直角三角形,
∴AF=BF,
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,
∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中,
,
∴△AEF≌△BCF(ASA).
18.解:∵DE=EB
∴设∠BDE=∠ABD=x,
∴∠AED=∠BDE+∠ABD=2x,
∵AD=DE,
∴∠AED=∠A=2x,
∴∠BDC=∠A+∠ABD=3x,
∵BD=BC,
∴∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,3x+3x+2x=180°,
解得x=22.5°,
∴∠A=2x=22.5°×2=45°.
《等腰三角形》课时练习
一、选择题
1.一个等腰三角形的一边长是7cm,另一边长为5cm,那么这个等腰三角形的周长是( )
A.12cm B.17cm C.19cm D.17cm或19cm
2.等腰三角形的一个角是80°,则它的底角是( )
A.50° B.80° C.50°或80° D.20°或80°
3.若一个等腰三角形的两边长分别是2和5,则它的周长为( )
A.12 B.9 C.12或9 D.9或7
4.如图,在△ABC中,AB=AC=4,∠ABC和∠ACB的平分线交于点E,过点E作MN∥BC分别交AB、AC于M、N,则△AMN的周长为( )
A.12 B.4 C.8 D.不确定
5.如果等腰三角形的一个底角为α,那么( )
A.α不大于45° B.0°<α<90° C.α不大于90° D.45°<α<90°
6.等腰三角形的一个内角为70°,则另外两个内角的度数分别是(??? )
A.55°,55°????? B.70°,40°或70°,55°
C.70°,40°??? D.55°,55°或70°,40°
7.下列关于等腰三角形的性质叙述错误的是(??? )
A.等腰三角形的两底角相等
B.等腰三角形的两边相等
C.等腰三角形是轴对称图形
D.等腰三角形底边上的高、底边上的中线、顶角的平分线互相重合
8.如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( )
A.1个 B.3个 C.4个 D.5个
9.如图,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK,BN=AK,若∠MKN=44°,则∠P的度数为( )
A.102° B.100° C.88° D.92°
10.在△ABC中,AB=AC,D、E分别在BC、AC上,AD=AE,∠CDE=20°,∠BAD度数为( )
A.36° B.40° C.45° D.50°
二、填空题
11.一个三角形等腰三角形的两边长分别为13和7,则周长为 .
12.如图,在△ABC中,AB=AC,AD⊥BC于D点,点E、F分别是AD的三等分点,若△ABC的面积为18cm2,则图中阴影部分面积为 cm2.
13.如图,在Rt△ABC中,D,E为斜边AB上的两个点,且BD=BC,AE=AC,
则∠DCE的大小为 (度).
14.在等腰三角形中,
(1)一腰上的高与底边的夹角为30°,则顶角为 .
(2)一腰上的高与另一腰的夹角为30°,则顶角为 .
三、解答题
15.如图,在△ABC中,AB=AC,D为BC边上一点,∠B=30°,∠DAB=45°.
(1)求∠DAC的度数;
(2)求证:DC=AB.
16.如图所示,已知在△ABC中,AB=AD=DC,∠BAD=26°,求∠B和∠C的度数.
17.如图1,在△ABC中,AB=AC,点D是BC的中点,点E在AD上.
(1)求证:BE=CE;
(2)如图2,若BE的延长线交AC于点F,且BF⊥AC,垂足为F,∠BAC=45°,原题设其它条件不变.求证:△AEF≌△BCF.
18.如图,在△ABC中,AB=AC,D、E分别在AC、AB边上,且BC=BD,AD=DE=EB,
求∠A的度数.
参考答案
1.D
2.C
3.A
4.C
5.B
6.D
7.B
8.D
9.D
10.B
11.答案为:33或27.
12.答案为:9.
13.答案为:45.
14.答案为:60°或120°.
15. (1)解:∵AB=AC,∴∠B=∠C=30°,
∵∠C+∠BAC+∠B=180°,∴∠BAC=180°﹣30°﹣30°=120°,
∵∠DAB=45°,∴∠DAC=∠BAC﹣∠DAB=120°﹣45°=75°;
(2)证明:∵∠DAB=45°,∴∠ADC=∠B+∠DAB=75°,
∴∠DAC=∠ADC,∴DC=AC,∴DC=AB.
16.解:在△ABC中,AB=AD=DC,
∵AB=AD,在三角形ABD中,∠B=∠ADB=(180°﹣26°)×=77°,
又∵AD=DC,在三角形ADC中,
∴∠C==77°×=38.5°.
17.证明:(1)∵AB=AC,D是BC的中点,
∴∠BAE=∠EAC,
在△ABE和△ACE中,,
∴△ABE≌△ACE(SAS),
∴BE=CE;
(2)∵∠BAC=45°,BF⊥AF,
∴△ABF为等腰直角三角形,
∴AF=BF,
∵AB=AC,点D是BC的中点,
∴AD⊥BC,
∴∠EAF+∠C=90°,
∵BF⊥AC,
∴∠CBF+∠C=90°,
∴∠EAF=∠CBF,
在△AEF和△BCF中,
,
∴△AEF≌△BCF(ASA).
18.解:∵DE=EB
∴设∠BDE=∠ABD=x,
∴∠AED=∠BDE+∠ABD=2x,
∵AD=DE,
∴∠AED=∠A=2x,
∴∠BDC=∠A+∠ABD=3x,
∵BD=BC,
∴∠C=∠BDC=3x,
∵AB=AC,
∴∠ABC=∠C=3x,
在△ABC中,3x+3x+2x=180°,
解得x=22.5°,
∴∠A=2x=22.5°×2=45°.
