青岛版六年级上册数学 第5单元测试 8.圆的面积(含答案)
文档属性
| 名称 | 青岛版六年级上册数学 第5单元测试 8.圆的面积(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 95.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-04 00:00:00 | ||
图片预览


文档简介
核心考点突破卷
8.圆的面积
一、填空。(每空1分,共15分)
1.一个圆的半径是30厘米,它的面积是( )平方分米。
2.钟面上的分针长6
cm,时针从3时走到4时,分针扫过的面积是( )cm2。
3.圆的周长是12.56厘米,它的直径是( )厘米,半径是
( )厘米,面积是( )平方厘米。
4.把一个圆平均分成若干个小扇形,再拼成一个近似的长方形,这个长方形长相当于圆的(
),宽相当于圆的(
),因为长方形的面积=长×宽,所以圆的面积S=( )×( )=( )。
5.在一块边长是20厘米的正方形纸板上剪下一个最大的圆,这个圆的周长是( )厘米,面积是( )平方厘米,剩下部分的面积是( )平方厘米。
6.有一个环形,外圆的半径是4厘米,内圆的半径是2厘米,这个环形的面积是( )平方厘米。
7.李叔叔家依墙修建了一个半圆形水池,并在水池的弧形外圈围了一条彩灯带,彩灯带总长是9.42米,这个半圆形水池的占地面积是( )平方米。
二、判断。(每题3分,共15分)
1.圆心角越大,扇形的面积就越大。
( )
2.一个圆的半径越大,这个圆的面积就越大。
( )
3.一个直径是4分米的圆,它的周长和面积相等。
( )
4.两个圆的周长相等,它们的面积也相等。
( )
5.如果大圆半径是小圆半径的2倍,那么大圆面积也是小圆面积的2倍。
( )
三、选择。(每题3分,共15分)
1.如图,在研究圆环面积时,小明借助研究圆面积的方法,把圆环等分成16份,拼成一个近似的平行四边形。他发现平行四边形的底是( )。(外圆和内圆的半径分别是R和r)
A.πR
B.πr
C.πR+πr
D.πR-
πr
2.计算圆的面积,可以选择的方法是( )。
A.S=πr2
B.S=π(d÷2)2
C.S=π(C÷2π)2
D.以上3种都可以
3.一个圆环,外圆半径是内圆半径的3倍,这个圆环的面积是内圆面积的( )。
A.3倍
B.8倍
C.9倍
D.6倍
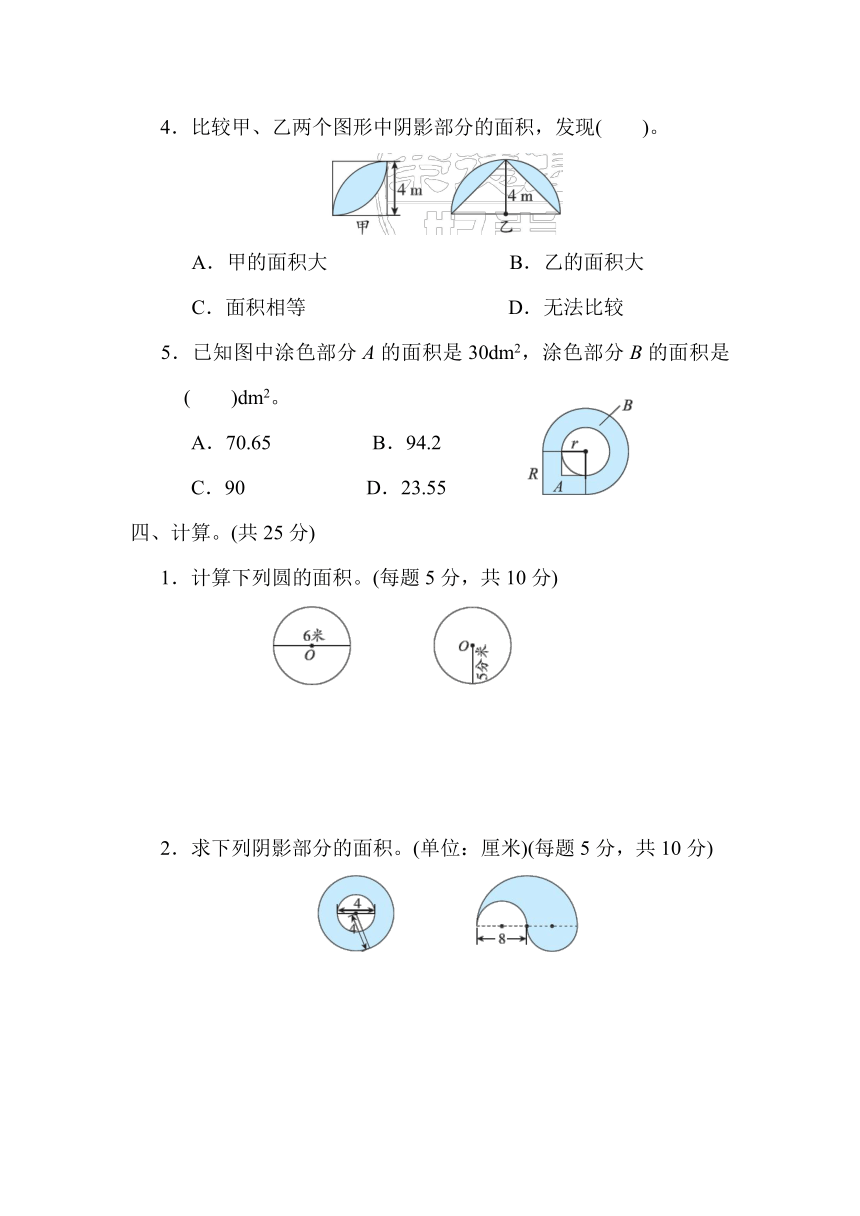
4.比较甲、乙两个图形中阴影部分的面积,发现( )。
A.甲的面积大
B.乙的面积大
C.面积相等
D.无法比较
5.已知图中涂色部分A的面积是30dm2,涂色部分B的面积是( )dm2。
A.70.65
B.94.2
C.90
D.23.55
四、计算。(共25分)
1.计算下列圆的面积。(每题5分,共10分)
2.求下列阴影部分的面积。(单位:厘米)(每题5分,共10分)
3.如图,正方形的面积是24平方厘米,求阴影部分的面积。
(5分)
五、解决问题。(共30分)
1.寿光某蔬菜大棚安装的自动浇灌器最远能喷水5米,这个自动浇灌器旋转一周最多能浇灌多少平方米?(6分)
2.运河公园修了一个圆形水池,水池的周长是50.24米,它的占地面积是多少平方米?(6分)
3.老师们在靠墙处用篱笆围了一块半圆形的地作为“百草基地”(如图),篱笆长25.12米。“百草基地”的面积是多少平方米?(6分)
4.小军和小明到圆形广场去散步。他们从圆形广场边缘的同一地点同时出发,相背而行,4分钟后两人相遇。小军每分钟走
75米,小明每分钟走82米。这个圆形广场的占地面积是多少平方米?(6分)
5.把一只羊拴在一块长8米、宽6米的长方形草地上,拴羊的绳长2米,这只羊能吃到的草的最大面积是多少平方米?如果要使羊吃草的面积最小,那么应该将羊拴在这个长方形草地的什么位置?最小面积为多少平方米?(6分)
答案
一、1.28.26
2.113.04
3.4 2 12.56
4.周长的一半 半径 C r πr2
5.62.8 314 86
6.37.68
7.14.13
二、1.× 2.√ 3.× 4.√ 5.×
三、1.C 2.D 3.B 4.C
5.A 【点拨】涂色部分A的面积=R2-r2=30(dm2),因为涂色部分B的面积是环形面积的,所以涂色部分B的面积为
(R2-r2)×3.14×=30×3.14×=70.65(dm2),所以选A。
四、1.(6÷2)2×3.14=28.26(平方米)
52×3.14=78.5(平方分米)
2.[42-(4÷2)2]×3.14=37.68(平方厘米)
82×3.14×=100.48(平方厘米)
3.24×3.14×=56.52(平方厘米)
五、1.52×3.14=78.5(平方米)
答:这个自动浇灌器旋转一周最多能浇灌78.5平方米。
2.(50.24÷3.14÷2)2×3.14=200.96(平方米)
答:它的占地面积是200.96平方米。
3.(25.12÷3.14)2×3.14÷2=100.48(平方米)
答:“百草基地”的面积是100.48平方米。
【点拨】25.12米是圆的周长的一半,也就是πr,即πr=25.12米,所以r=25.12÷3.14(米),从而求出半圆形的面积为(25.12÷3.14)2×3.14÷2=100.48(平方米)。
4.[(75+82)×4÷3.14÷2]2×3.14=31400(平方米)
答:这个圆形广场的占地面积是31400平方米。
5.3.14
×22=12.56(平方米)
12.56÷4=3.14(平方米)
答:这只羊能吃到的草的最大面积是12.56平方米,如果要使羊吃草的面积最小,那么应该将羊拴在这个长方形草地的直角顶点上,最小面积是3.14平方米。
8.圆的面积
一、填空。(每空1分,共15分)
1.一个圆的半径是30厘米,它的面积是( )平方分米。
2.钟面上的分针长6
cm,时针从3时走到4时,分针扫过的面积是( )cm2。
3.圆的周长是12.56厘米,它的直径是( )厘米,半径是
( )厘米,面积是( )平方厘米。
4.把一个圆平均分成若干个小扇形,再拼成一个近似的长方形,这个长方形长相当于圆的(
),宽相当于圆的(
),因为长方形的面积=长×宽,所以圆的面积S=( )×( )=( )。
5.在一块边长是20厘米的正方形纸板上剪下一个最大的圆,这个圆的周长是( )厘米,面积是( )平方厘米,剩下部分的面积是( )平方厘米。
6.有一个环形,外圆的半径是4厘米,内圆的半径是2厘米,这个环形的面积是( )平方厘米。
7.李叔叔家依墙修建了一个半圆形水池,并在水池的弧形外圈围了一条彩灯带,彩灯带总长是9.42米,这个半圆形水池的占地面积是( )平方米。
二、判断。(每题3分,共15分)
1.圆心角越大,扇形的面积就越大。
( )
2.一个圆的半径越大,这个圆的面积就越大。
( )
3.一个直径是4分米的圆,它的周长和面积相等。
( )
4.两个圆的周长相等,它们的面积也相等。
( )
5.如果大圆半径是小圆半径的2倍,那么大圆面积也是小圆面积的2倍。
( )
三、选择。(每题3分,共15分)
1.如图,在研究圆环面积时,小明借助研究圆面积的方法,把圆环等分成16份,拼成一个近似的平行四边形。他发现平行四边形的底是( )。(外圆和内圆的半径分别是R和r)
A.πR
B.πr
C.πR+πr
D.πR-
πr
2.计算圆的面积,可以选择的方法是( )。
A.S=πr2
B.S=π(d÷2)2
C.S=π(C÷2π)2
D.以上3种都可以
3.一个圆环,外圆半径是内圆半径的3倍,这个圆环的面积是内圆面积的( )。
A.3倍
B.8倍
C.9倍
D.6倍
4.比较甲、乙两个图形中阴影部分的面积,发现( )。
A.甲的面积大
B.乙的面积大
C.面积相等
D.无法比较
5.已知图中涂色部分A的面积是30dm2,涂色部分B的面积是( )dm2。
A.70.65
B.94.2
C.90
D.23.55
四、计算。(共25分)
1.计算下列圆的面积。(每题5分,共10分)
2.求下列阴影部分的面积。(单位:厘米)(每题5分,共10分)
3.如图,正方形的面积是24平方厘米,求阴影部分的面积。
(5分)
五、解决问题。(共30分)
1.寿光某蔬菜大棚安装的自动浇灌器最远能喷水5米,这个自动浇灌器旋转一周最多能浇灌多少平方米?(6分)
2.运河公园修了一个圆形水池,水池的周长是50.24米,它的占地面积是多少平方米?(6分)
3.老师们在靠墙处用篱笆围了一块半圆形的地作为“百草基地”(如图),篱笆长25.12米。“百草基地”的面积是多少平方米?(6分)
4.小军和小明到圆形广场去散步。他们从圆形广场边缘的同一地点同时出发,相背而行,4分钟后两人相遇。小军每分钟走
75米,小明每分钟走82米。这个圆形广场的占地面积是多少平方米?(6分)
5.把一只羊拴在一块长8米、宽6米的长方形草地上,拴羊的绳长2米,这只羊能吃到的草的最大面积是多少平方米?如果要使羊吃草的面积最小,那么应该将羊拴在这个长方形草地的什么位置?最小面积为多少平方米?(6分)
答案
一、1.28.26
2.113.04
3.4 2 12.56
4.周长的一半 半径 C r πr2
5.62.8 314 86
6.37.68
7.14.13
二、1.× 2.√ 3.× 4.√ 5.×
三、1.C 2.D 3.B 4.C
5.A 【点拨】涂色部分A的面积=R2-r2=30(dm2),因为涂色部分B的面积是环形面积的,所以涂色部分B的面积为
(R2-r2)×3.14×=30×3.14×=70.65(dm2),所以选A。
四、1.(6÷2)2×3.14=28.26(平方米)
52×3.14=78.5(平方分米)
2.[42-(4÷2)2]×3.14=37.68(平方厘米)
82×3.14×=100.48(平方厘米)
3.24×3.14×=56.52(平方厘米)
五、1.52×3.14=78.5(平方米)
答:这个自动浇灌器旋转一周最多能浇灌78.5平方米。
2.(50.24÷3.14÷2)2×3.14=200.96(平方米)
答:它的占地面积是200.96平方米。
3.(25.12÷3.14)2×3.14÷2=100.48(平方米)
答:“百草基地”的面积是100.48平方米。
【点拨】25.12米是圆的周长的一半,也就是πr,即πr=25.12米,所以r=25.12÷3.14(米),从而求出半圆形的面积为(25.12÷3.14)2×3.14÷2=100.48(平方米)。
4.[(75+82)×4÷3.14÷2]2×3.14=31400(平方米)
答:这个圆形广场的占地面积是31400平方米。
5.3.14
×22=12.56(平方米)
12.56÷4=3.14(平方米)
答:这只羊能吃到的草的最大面积是12.56平方米,如果要使羊吃草的面积最小,那么应该将羊拴在这个长方形草地的直角顶点上,最小面积是3.14平方米。
