青岛版数学五年级上册 四 走进动物园——简易方程 信息窗5 列方程解决问题(2)课件(34张ppt)
文档属性
| 名称 | 青岛版数学五年级上册 四 走进动物园——简易方程 信息窗5 列方程解决问题(2)课件(34张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 13:43:57 | ||
图片预览







文档简介
(共34张PPT)
列方程解决问题(2)
青岛版数学五年级(上)
四 走进动物园
——简易方程
会解形如ax±b=c和ax±bx=c类型的方程并掌握其方法。
学会借助线段图理解数量之间的相等关系,并能解决实际问题。
培养分析问题和解决问题的能力。初步形成正确的数学思想。
学习目标
【重点】
解形如ax±b=c和ax±bx=c类型的方程。
【难点】
借助线段图理解数量之间的相等关系,并能解决实际问题。
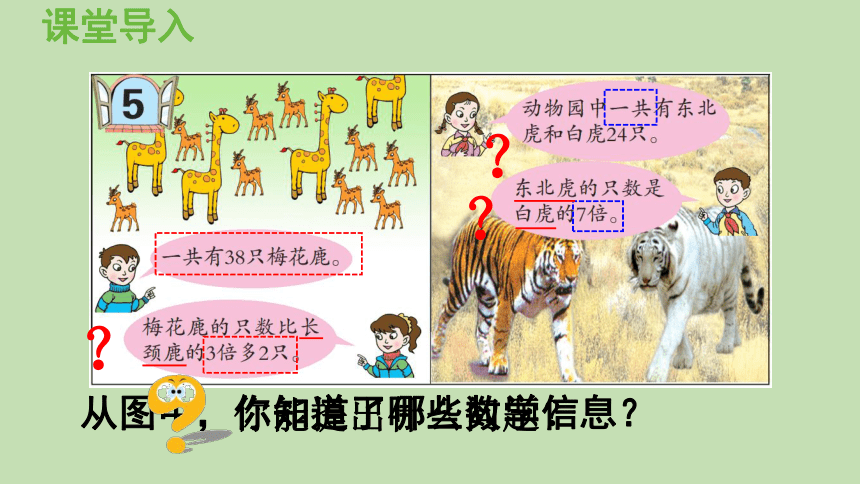
从图中,你知道了哪些数学信息?
?
你能提出什么问题?
?
?
课堂导入
长颈鹿有多少只?
有 38 只梅花鹿;
梅花鹿的只数比长颈鹿的 3 倍多 2 只。
先分析梅花鹿的只数与长颈鹿的只数之间的关系。
新知探究
长颈鹿:
梅花鹿:
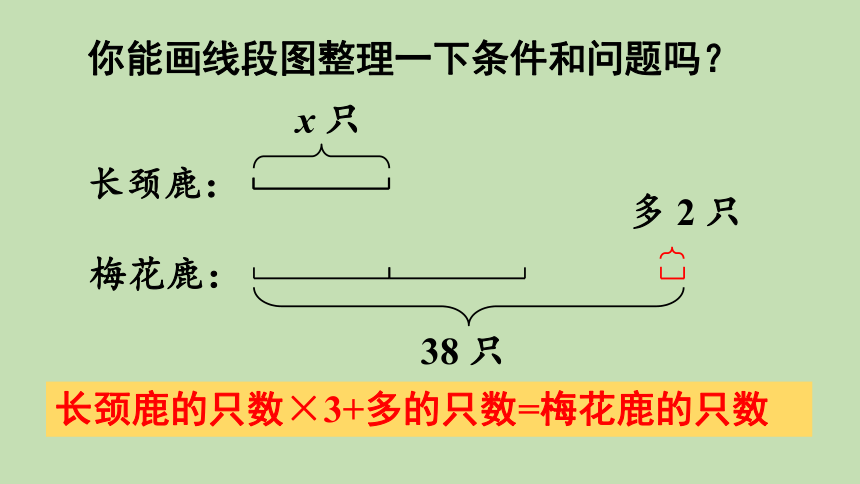
你能画线段图整理一下条件和问题吗?
x 只
38 只
多 2 只
长颈鹿的只数×3+多的只数=梅花鹿的只数
解:设长颈鹿有 x 只。
3x + 2 = 38
3x + 2 – 2 = 38 – 2
3x÷3 = 36÷3
x = 12
答:长颈鹿有 12 只。
这一步的依据是什么?
这一步的依据是什么?
你能试着用等式的性质解这种形式的方程吗?
再根据等量关系列方程解答。
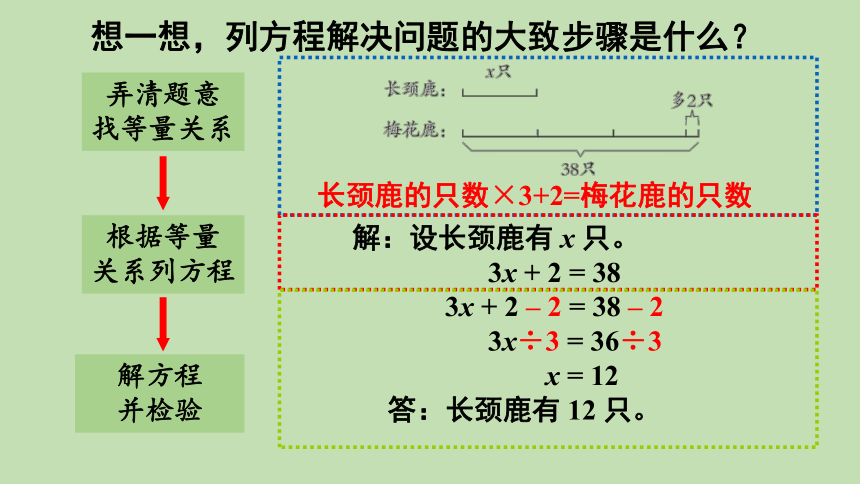
想一想,列方程解决问题的大致步骤是什么?
弄清题意
找等量关系
根据等量
关系列方程
解方程
并检验
长颈鹿的只数×3+2=梅花鹿的只数
解:设长颈鹿有 x 只。
3x + 2 = 38
3x + 2 – 2 = 38 – 2
3x÷3 = 36÷3
x = 12
答:长颈鹿有 12 只。
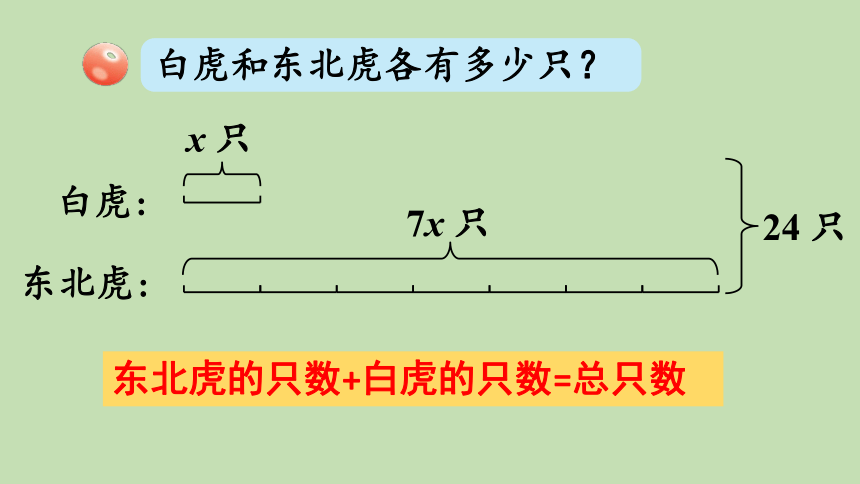
白虎和东北虎各有多少只?
白虎:
东北虎:
x 只
7x 只
东北虎的只数+白虎的只数=总只数
24 只
解:设白虎有 x 只,那么东北虎有 7x 只。
7x + x = 24
8x = 24
x = 3
7x = 7×3 = 21
答:白虎有 3 只,东北虎有 21 只。
7 个 x 与 1 个 x 合起来等于 8 个 x。
等量关系式:_________________________
方程:_____________
1. 看图写出等量关系式,并列方程解答。
3x – 25 = 200
客车的速度×3–少的千米数=动车的速度
课堂练习
(教材第61页“第1题”)
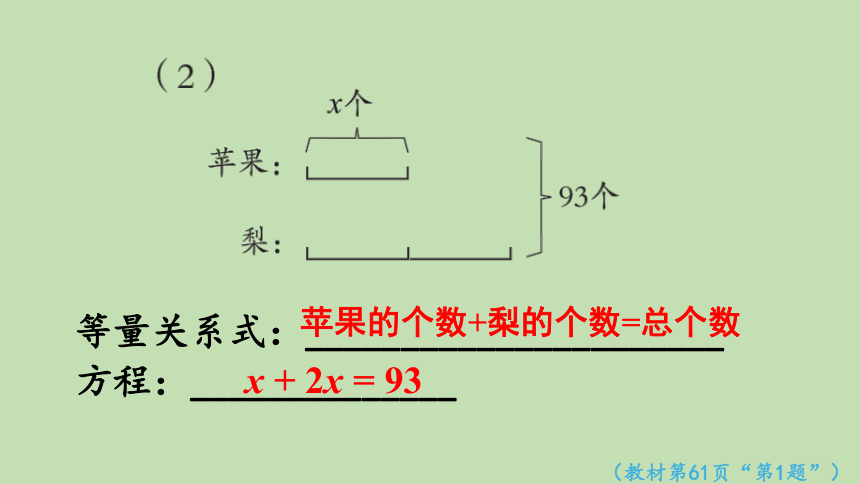
等量关系式:______________________
方程:______________
苹果的个数+梨的个数=总个数
x + 2x = 93
(教材第61页“第1题”)
2. 青藏铁路全长 1956 千米,比山东胶济铁路的 4 倍还多 384 千米。胶济铁路长多少千米?(先写出等量关系式,再列方程解答)
山东胶济铁路的长度×4 + 多的千米数 = 青藏铁路全长
(教材第61页“第2题”)
解:设胶济铁路长 x 千米。
4x + 384 = 1956
4x = 1572
4x + 384 – 384 = 1956 – 384
4x ÷ 4 = 1572 ÷ 4
x = 393
答:胶济铁路长 393 千米。
(教材第61页“第2题”)
3.8 x – x = 0.56
解:2.8x = 0.56
2.8x÷2.8 = 0.56÷2.8
x = 0.2
5x + 15 = 120
解:5x + 15 – 15 = 120 – 15
5x = 105
x = 21
5x÷5 = 105 ÷5
3.解方程。
(教材第62页“第3题”节选)
7x + 3x + 26 = 74
解: 10x + 26 = 74
10x + 26 – 26 = 74 – 26
10x = 48
x = 4.8
x – 0.85 x = 3
解:0.15x = 3
0.15x÷0.15 = 3÷0.15
x = 20
10x÷10 = 48÷10
(教材第62页“第3题”节选)
4. 柏树和松树一共有7500棵。柏树的棵数是松树的1.5倍。两种树各有多少棵?(先写出等量关系式,再列方程解答)
松树的棵数+柏树的棵数 =总棵数
(教材第62页“第4题”)
解:设松树有 x 棵,则柏树有 1.5x 棵。
x + 1.5x = 7500
2.5x = 7500
x = 3000
1.5x = 1.5×3000 = 4500
答:松树有 3000 棵,柏树有 4500 棵。
(教材第62页“第4题”)
5. 蜗牛、乌龟的爬行速度分别是多少?
(教材第62页“第5题”)
解:设蜗牛的爬行速度是每分钟 x 米。
30x = 27
x = 0.9
解:设乌龟的爬行速度是每分钟 y 米.
4y + 3 = 27
y = 6
答:蜗牛的速度是0.9米/分,乌龟的速度是6米/分。
(教材第62页“第5题”)
6. 一个长方形池塘的周长是 300 米。它的长是 100 米,宽是多少米?
解:设宽是 x 米。
答:宽是 50 米。
(100 + x)×2 = 300
(100 + x)×2÷2 = 300÷2
100 + x = 150
100 + x – 100 = 150 – 100
x = 50
(教材第62页“第6题”)
7. 2011年我国民用汽车保有量为105578万辆,比2001年保有量的58倍还多1062万辆。2001年我国民用汽车保有量是多少万辆?
如果设2001年我国民用汽车保有量是x万辆,下面哪个方程是正确的?在后面画“√”。
(1) 58x + 1062 = 105578 ( )
(2) 58x – 1062 = 105578 ( )
(3) 58x = 105578 + 1062 ( )
√
(教材第62页“第7题”)
8. 列方程解答。
(1)学校舞蹈队有女生 36 人,女生人数比男生的3倍少 12 人。男生有多少人?
解:设男生有 x 人。
3x – 12 = 36
x = 16
答:男生有16人。
(教材第62页“第8题”)
小红买 10 张花的钱数–小丽买 8 张花的钱数= 多花的钱数
(2)小红和小丽去买一种奥运纪念邮票。小红买了 10 张,小丽买了 8 张,小红比小丽多用了 6 元。每张邮票多少元?
(教材第62页“第8题”)
解:设每张邮票 x 元。
2x = 6
10x – 8x = 6
2x÷2 = 6÷2
x = 3
答:每张邮票 3 元。
(教材第62页“第8题”)
9.
(1)宝宝的体重是多少?
解:设宝宝的体重是 x 千克。
x + 58 = 67
x = 9
答:宝宝的体重是9千克。
(教材第63页“第9题”)
9.
(2)爸爸的体重比宝宝的7 倍还多 8 千克。爸爸的体重是多少?
9×7+8=71(千克)
答:爸爸的体重是 71千克。
(教材第63页“第9题”)
10. 列方程解答。
解:设一张光盘 x 元。
5x – 3x = 20
x = 10
答:一张光盘10元。
(教材第63页“第10题”)
解:设小光的身高是 x 厘米,则姚明的身高是 2x 厘米。
2x – x = 113
x = 113
2x = 2×113 = 226
答:小明的身高是113厘米,姚明的身高是226厘米。
(教材第63页“第10题”)
11. 白云山小学本学期转入 38 人,转出 24 人,现在一共有学生 845 人。白云山小学上学期有学生多少人?
解:设白云山小学上学期有学生 x 人。
x + 38 – 24 = 845
x = 831
答:白云山小学上学期有学生831人。
(教材第63页“第11题”)
12. 王刚家与李红家相距 840 米。王刚去给李红送书,为节省时间,两人同时从家出发。王刚平均每分钟走 63 米,李红平均每分钟走 57 米。几分钟后两人相遇?
(教材第63页“第12题”)
解:设 x 分钟后两人相遇。
840米
王刚走的路程
李红走的路程
63x
57x
12. 王刚家与李红家相距 840 米。王刚去给李红送书,为节省时间,两人同时从家出发。王刚平均每分钟走 63 米,李红平均每分钟走 57 米。几分钟后两人相遇?
解:设 x 分钟后两人相遇。
63x + 57x = 840
x = 7
答:7分钟后两人相遇.
(教材第63页“第12题”)
弄清题意
找等量关系
设未知数
列方程
解方程并检验
课堂小结
想一想:列方程解决问题的一般步骤是什么?
课后作业
作业课件中的相关练习。
02
01
课后练习。
列方程解决问题(2)
青岛版数学五年级(上)
四 走进动物园
——简易方程
会解形如ax±b=c和ax±bx=c类型的方程并掌握其方法。
学会借助线段图理解数量之间的相等关系,并能解决实际问题。
培养分析问题和解决问题的能力。初步形成正确的数学思想。
学习目标
【重点】
解形如ax±b=c和ax±bx=c类型的方程。
【难点】
借助线段图理解数量之间的相等关系,并能解决实际问题。
从图中,你知道了哪些数学信息?
?
你能提出什么问题?
?
?
课堂导入
长颈鹿有多少只?
有 38 只梅花鹿;
梅花鹿的只数比长颈鹿的 3 倍多 2 只。
先分析梅花鹿的只数与长颈鹿的只数之间的关系。
新知探究
长颈鹿:
梅花鹿:
你能画线段图整理一下条件和问题吗?
x 只
38 只
多 2 只
长颈鹿的只数×3+多的只数=梅花鹿的只数
解:设长颈鹿有 x 只。
3x + 2 = 38
3x + 2 – 2 = 38 – 2
3x÷3 = 36÷3
x = 12
答:长颈鹿有 12 只。
这一步的依据是什么?
这一步的依据是什么?
你能试着用等式的性质解这种形式的方程吗?
再根据等量关系列方程解答。
想一想,列方程解决问题的大致步骤是什么?
弄清题意
找等量关系
根据等量
关系列方程
解方程
并检验
长颈鹿的只数×3+2=梅花鹿的只数
解:设长颈鹿有 x 只。
3x + 2 = 38
3x + 2 – 2 = 38 – 2
3x÷3 = 36÷3
x = 12
答:长颈鹿有 12 只。
白虎和东北虎各有多少只?
白虎:
东北虎:
x 只
7x 只
东北虎的只数+白虎的只数=总只数
24 只
解:设白虎有 x 只,那么东北虎有 7x 只。
7x + x = 24
8x = 24
x = 3
7x = 7×3 = 21
答:白虎有 3 只,东北虎有 21 只。
7 个 x 与 1 个 x 合起来等于 8 个 x。
等量关系式:_________________________
方程:_____________
1. 看图写出等量关系式,并列方程解答。
3x – 25 = 200
客车的速度×3–少的千米数=动车的速度
课堂练习
(教材第61页“第1题”)
等量关系式:______________________
方程:______________
苹果的个数+梨的个数=总个数
x + 2x = 93
(教材第61页“第1题”)
2. 青藏铁路全长 1956 千米,比山东胶济铁路的 4 倍还多 384 千米。胶济铁路长多少千米?(先写出等量关系式,再列方程解答)
山东胶济铁路的长度×4 + 多的千米数 = 青藏铁路全长
(教材第61页“第2题”)
解:设胶济铁路长 x 千米。
4x + 384 = 1956
4x = 1572
4x + 384 – 384 = 1956 – 384
4x ÷ 4 = 1572 ÷ 4
x = 393
答:胶济铁路长 393 千米。
(教材第61页“第2题”)
3.8 x – x = 0.56
解:2.8x = 0.56
2.8x÷2.8 = 0.56÷2.8
x = 0.2
5x + 15 = 120
解:5x + 15 – 15 = 120 – 15
5x = 105
x = 21
5x÷5 = 105 ÷5
3.解方程。
(教材第62页“第3题”节选)
7x + 3x + 26 = 74
解: 10x + 26 = 74
10x + 26 – 26 = 74 – 26
10x = 48
x = 4.8
x – 0.85 x = 3
解:0.15x = 3
0.15x÷0.15 = 3÷0.15
x = 20
10x÷10 = 48÷10
(教材第62页“第3题”节选)
4. 柏树和松树一共有7500棵。柏树的棵数是松树的1.5倍。两种树各有多少棵?(先写出等量关系式,再列方程解答)
松树的棵数+柏树的棵数 =总棵数
(教材第62页“第4题”)
解:设松树有 x 棵,则柏树有 1.5x 棵。
x + 1.5x = 7500
2.5x = 7500
x = 3000
1.5x = 1.5×3000 = 4500
答:松树有 3000 棵,柏树有 4500 棵。
(教材第62页“第4题”)
5. 蜗牛、乌龟的爬行速度分别是多少?
(教材第62页“第5题”)
解:设蜗牛的爬行速度是每分钟 x 米。
30x = 27
x = 0.9
解:设乌龟的爬行速度是每分钟 y 米.
4y + 3 = 27
y = 6
答:蜗牛的速度是0.9米/分,乌龟的速度是6米/分。
(教材第62页“第5题”)
6. 一个长方形池塘的周长是 300 米。它的长是 100 米,宽是多少米?
解:设宽是 x 米。
答:宽是 50 米。
(100 + x)×2 = 300
(100 + x)×2÷2 = 300÷2
100 + x = 150
100 + x – 100 = 150 – 100
x = 50
(教材第62页“第6题”)
7. 2011年我国民用汽车保有量为105578万辆,比2001年保有量的58倍还多1062万辆。2001年我国民用汽车保有量是多少万辆?
如果设2001年我国民用汽车保有量是x万辆,下面哪个方程是正确的?在后面画“√”。
(1) 58x + 1062 = 105578 ( )
(2) 58x – 1062 = 105578 ( )
(3) 58x = 105578 + 1062 ( )
√
(教材第62页“第7题”)
8. 列方程解答。
(1)学校舞蹈队有女生 36 人,女生人数比男生的3倍少 12 人。男生有多少人?
解:设男生有 x 人。
3x – 12 = 36
x = 16
答:男生有16人。
(教材第62页“第8题”)
小红买 10 张花的钱数–小丽买 8 张花的钱数= 多花的钱数
(2)小红和小丽去买一种奥运纪念邮票。小红买了 10 张,小丽买了 8 张,小红比小丽多用了 6 元。每张邮票多少元?
(教材第62页“第8题”)
解:设每张邮票 x 元。
2x = 6
10x – 8x = 6
2x÷2 = 6÷2
x = 3
答:每张邮票 3 元。
(教材第62页“第8题”)
9.
(1)宝宝的体重是多少?
解:设宝宝的体重是 x 千克。
x + 58 = 67
x = 9
答:宝宝的体重是9千克。
(教材第63页“第9题”)
9.
(2)爸爸的体重比宝宝的7 倍还多 8 千克。爸爸的体重是多少?
9×7+8=71(千克)
答:爸爸的体重是 71千克。
(教材第63页“第9题”)
10. 列方程解答。
解:设一张光盘 x 元。
5x – 3x = 20
x = 10
答:一张光盘10元。
(教材第63页“第10题”)
解:设小光的身高是 x 厘米,则姚明的身高是 2x 厘米。
2x – x = 113
x = 113
2x = 2×113 = 226
答:小明的身高是113厘米,姚明的身高是226厘米。
(教材第63页“第10题”)
11. 白云山小学本学期转入 38 人,转出 24 人,现在一共有学生 845 人。白云山小学上学期有学生多少人?
解:设白云山小学上学期有学生 x 人。
x + 38 – 24 = 845
x = 831
答:白云山小学上学期有学生831人。
(教材第63页“第11题”)
12. 王刚家与李红家相距 840 米。王刚去给李红送书,为节省时间,两人同时从家出发。王刚平均每分钟走 63 米,李红平均每分钟走 57 米。几分钟后两人相遇?
(教材第63页“第12题”)
解:设 x 分钟后两人相遇。
840米
王刚走的路程
李红走的路程
63x
57x
12. 王刚家与李红家相距 840 米。王刚去给李红送书,为节省时间,两人同时从家出发。王刚平均每分钟走 63 米,李红平均每分钟走 57 米。几分钟后两人相遇?
解:设 x 分钟后两人相遇。
63x + 57x = 840
x = 7
答:7分钟后两人相遇.
(教材第63页“第12题”)
弄清题意
找等量关系
设未知数
列方程
解方程并检验
课堂小结
想一想:列方程解决问题的一般步骤是什么?
课后作业
作业课件中的相关练习。
02
01
课后练习。
