青岛版数学五年级上册 五 生活中的多边形——多边形的面积 回顾整理 课件(39张ppt)
文档属性
| 名称 | 青岛版数学五年级上册 五 生活中的多边形——多边形的面积 回顾整理 课件(39张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 13:44:41 | ||
图片预览









文档简介
回顾整理
青岛版数学五年级(上)
五 生活中的多边形
——多边形的面积
平行四边形的面积
S =ɑh
三角形的面积
S =ɑh÷2
梯形的面积
S =(ɑ+b)h÷2
组合图形的面积
转化成求几个简单的平面图形面积的和与差
多边形的面积
知识梳理
需要回顾整理的内容有哪些呢?
推导面积公式时都用了转化的方法。
平方
千米
公顷
平方米
平方
分米
平方
厘米
cm2
dm2
m2
km2
hm2
100
1000000
10000
100
100
“公顷”和“平方米”之间的进率是10000;
其他每相邻两个面积单位之间的进率都是100。
土地面积单位
常用的面积单位
面积单位
要点回顾
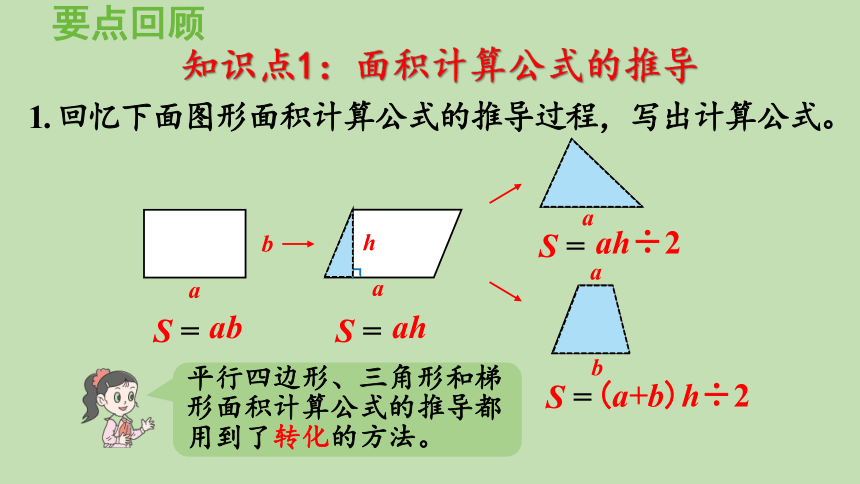
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点1:面积计算公式的推导
知识点2:面积的计算
2.计算下面图形的面积。
利用字母公式进行计算,先要找到相应的数值,再代入公式计算,最后还要加上单位。
S=ah
=270(cm2)
=18×15
S=ah÷2
=144(cm2)
=36×8÷2
S=a2
=3.61(m2)
=1.9×1.9
计算平行四边形、三角形时,还得注意底和高要相对应。
S=ah÷2
=3.41(m2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
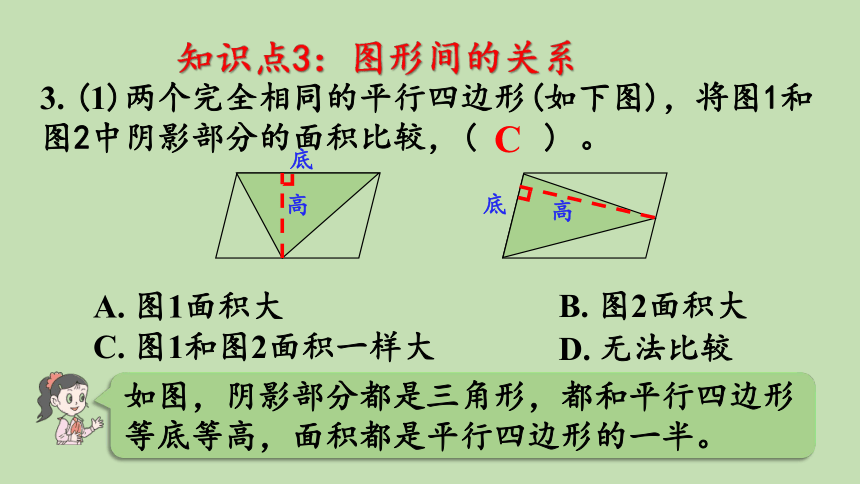
3. (1)两个完全相同的平行四边形(如下图),将图1和图2中阴影部分的面积比较,( ) 。
如图,阴影部分都是三角形,都和平行四边形等底等高,面积都是平行四边形的一半。
A. 图1面积大
B. 图2面积大
D. 无法比较
C. 图1和图2面积一样大
底
高
底
高
C
知识点3:图形间的关系
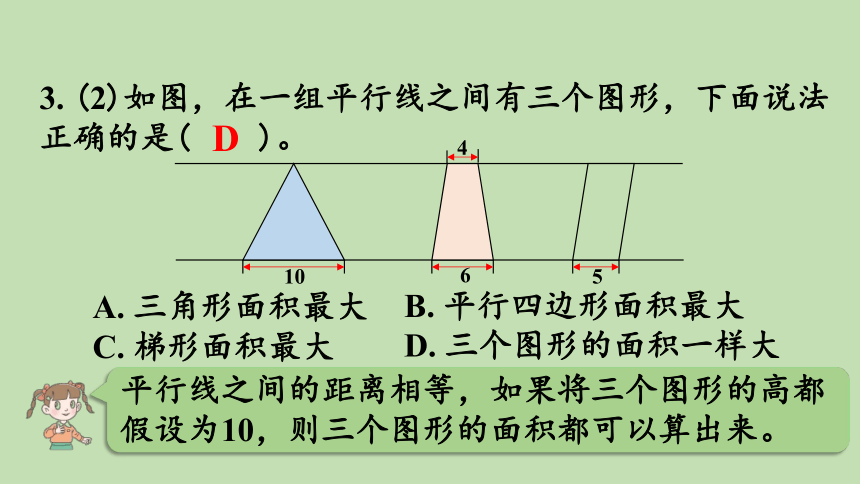
3. (2)如图,在一组平行线之间有三个图形,下面说法正确的是( )。
平行线之间的距离相等,如果将三个图形的高都假设为10,则三个图形的面积都可以算出来。
A. 三角形面积最大
B. 平行四边形面积最大
D. 三个图形的面积一样大
C. 梯形面积最大
10
5
6
4
D
图形间的面积比较,往往牵涉到图形间的关系:如三角形的面积是与它等底等高的平行四边形面积的一半等。
我们还经常用到如下这些规律:等底等高的平行四边形面积相等;等底等高的三角形面积相等;面积相等的平行四边形、三角形或梯形,形状不一定相同等。
知识点4:组合图形的面积计算
4. 计算右面图形的面积。你能想出几种方法?
组合图形的面积一般有两种思路:①分割法(求和);②添补法(求差)。
方法一:分割成长方形和三角形
S三角形=(10?5)×(12?6)÷2=15(cm2)
S长方形=12×5=60(cm2)
S=15+60=75(cm2)
方法二:分割成长方形和梯形
S长方形=6×5=30(cm2)
S梯形 =(5+10)×(12?6)÷2
=45(cm2)
S=30+45=75(cm2)
方法三:分割成三角形和梯形
S三角形=10×(12?6)÷2 =30(cm2)
S梯形=(6+12)×5÷2=45(cm2)
S=30+45=75(cm2)
方法四:添补成长方形
S长方形=12×10=120(cm2)
S梯形=(6+12)×(10?5)÷2
=45(cm2)
S=120?45=75(cm2)
组合图形的解法往往不止一种,但解题时应综合分析,尽量选用简便的方法计算。
知识点5:土地面积单位的实际应用
5.市政府开展“开荒造林”活动,打算在一块长18千米,
宽6千米的长方形荒地上种树,如果按平均每公顷种
树3500棵计算,大约能种多少棵树?
18×6=108(平方千米)
分析:要求能种多少棵树就要先求出这块地的面积。
3500×10800=3780 0000(棵)
答:大约能种3780 0000棵树。
108平方千米=10800公顷
解决跟面积有关的实际问题要注意单位换算哟!
(1)绿色小麦区的面积是多少平方米?每年可以生产多少千克优质小麦?
360×300=108000(平方米)
108000×0.75=81000(千克)
答:绿色小麦区的面积是108000平方米。每年可以生产81000千克优质小麦。
我学会了吗
(2)蔬菜区辣椒的产值每年约为多少元?
(240+360)×300÷2
=600×300÷2
90000×25=2250000(元)
=90000(平方米)
=180000÷2
答:蔬菜区辣椒的产值每年约为2250000元。
(3)果园占地面积一共是多少平方米?合多少公顷?
120×260÷2+240×120
=15600+28800
=44400(平方米)
=4.44(公顷)
答:果园占地面积一共是444000平方米。合4.44公顷。
(4)你还能提出什么数学问题?
问题:蔬菜区(二)占地面积一共是多少平方米?
240×240=57600(平方米)
答:蔬菜区(二)占地面积一共是57600平方米。
1. 量一量,算一算,求出下面图形的面积。(单位:厘米)
1cm
1.5cm
1.5cm
1.5cm
2.5cm
1.5cm
2.5cm
1cm
1.5cm
2.5cm
2cm
①1×1.5÷2=0.75(cm2)
②2.5×1.5=3.75(cm2)
③1.5×1.5=2.25(cm2)
④2.5×1=2.5(cm2)
⑤(1.5+2.5)×2÷2
=4×2÷2
=4(cm2)
(教材第82页“第1题” )
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形
平行四边形
三角形
梯形
底(米)
5.6
底3.上2
下底6.4
高(米)
2.5
7
面积(平方米)
84
43.2
2. 填表。
24
14
9
(教材第82页“第2题” )
3.
这块挡风玻璃的面积大约是多少?
(40+80)×30÷2
=120×30÷2
=1800(平方厘米)
答:这块挡风玻璃的面积大约是1800平方厘米。
(教材第82页“第3题” )
6.5公顷=( )平方米
1200公顷=( )平方千米
48000平方米=( )公顷
305平方分米=( )平方米
2平方分米5平方厘米=( )平方分米
4.填一填。
65000
12
4.8
3.05
2.05
(教材第82页“第4题” )
5.绿化队计划在一块近似平行四边形的空地里栽种一片防护林。如果每8平方米种一棵树,需要多少棵树苗?
120×30÷8=450(棵)
答:需要450棵树苗。
(教材第82页“第5题” )
6.下面是某拦河大坝的横截面示意图。请求出它
的面积。
答:它的面积是2000平方米。
(20+60)×50÷2
=80×50÷2
=2000(平方米)
(教材第82页“第6题” )
7.解方程。
5.2χ=26
χ=5
解:5.2χ÷5.2=26÷5.2
3χ-2.7=12.3
解:3χ-2.7+2.7=12.3+2.7
3χ=15
3χ÷3=15÷3
χ=5
0.6+χ=7.2
解:χ+0.6-0.6=7.2-0.6
χ=6.6
χ÷1.5=8
解:χ÷1.5×1.5=8×1.5
χ=12
(教材第83页“第7题” )
5χ+7χ=84
χ=7
解:12χ=84
12χ÷12=84÷12
3.8χ-0.8χ=4.5
χ=1.5
解:3χ=4.5
3χ÷3=4.5÷3
8. 求出下面图形的面积。
三角形的面积:8×6÷2 = 24(cm?)
平行四边形的面积:10×5 = 50(cm?)
梯形的面积:(6+10)×3÷2 = 24(cm?)
总面积:24+50+24 = 98(cm?)
(教材第83页“第8题” )
长方形的面积:12×5 = 60(cm?)
梯形的面积:(6+4)×3÷2 = 15(cm?)
总面积:60-15 = 45(cm?)
9.一块三角形菜地面积是1公顷。它的高为50米,它的底边长多少米?
1公顷= 10000(m?)
解:设底边是x米。
50χ÷2=10000
χ=400
答:底边长400米。
50χ÷2×2=10000×2
50χ=20000
50χ÷50=20000÷50
(教材第83页“第9题” )
10.在方格纸上画几个已学过的图形,并计算出它们的面积。(每个小方格表示1cm2)
?
长方形的面积:4×3 = 12(cm?)
正方形的面积:5×5 = 25(cm?)
(教材第83页“第10题” )
平行四边形的面积:4×3 = 12(cm?)
三角形的面积:6×4÷2 = 12(cm?)
梯形的面积:(2+8)×4÷2 = 20(cm?)
10.在方格纸上画几个已学过的图形,并计算出它们的面积。(每个小方格表示1cm2)
?
11.如果每平方米摆放20盆花,根据已知的数据,将表格填完整。
200
4000
200
4000
400
8000
(教材第83页“第11题” )
12.求χ的值。
解:设梯形的高是χ米。
10χ÷2 = 20
χ = 4
10χ÷2×2 = 20×2
10χ= 40
10χ÷10= 40÷10
(3+7)χ÷2 = 20
解:设平行四边形的底是χ米。
χ= 8
5χ= 40
5χ÷5= 40÷5
(教材第83页“第12题” )
13.
(1)这片树林一天能释放多少千克氧气?
800×500=400000(平方米)
400000平方米=4公顷
4×750=3000(千克)
答:这片树林一天能释放3000千克氧气。
(教材第84页“第13题” )
(2)这片树林一个月能吸收多少千克二氧化碳?
800×500=400000(平方米)
400000平方米=4公顷
4×950×30=114000(千克)
答:这片树林一个月能吸收114000千克二氧化碳。
13.
(3)你还能提出什么数学问题?
问题:这片树林一周能释放多少千克氧气?
800×500=400000(平方米)
400000平方米=4公顷
4×750×7=21000(千克)
答:这片树林一周能释放21000千克氧气。
13.
650÷(60+70)
=650÷130
=5(小时)
答:火车行驶了5小时。
(教材第84页“第14题” )
14.两列火车同时从滨海站出发,相背而行。开往富江站的火车平均速度为60千米/时,开往双山站的火车平均速度为70千米/时,结果两车正好同时到站。火车行驶了几小时?
15.
如果栽梨树,可以栽多少棵?如果栽苹果树呢?
(30+42)×20÷2
=72×20÷2
=1440÷2
=720(平方米)
梨树:720÷12=60(棵)
苹果树:720÷18=40(棵)
答:如果栽梨树可以栽60棵。如果栽苹果树可以栽40棵。
(教材第84页“第15题” )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每棵梨树的占地面积(m?)
12
每棵苹果树的占地面积(m?)
18
左面是一个果园的平面示意图。
做如图所示四个侧面完全相同的抽风机排气口,至少需要多少平方米的铁皮?
16.
(4+8)×6÷2×4
=12×6÷2×4
=144(平方分米)
=1.44(平方米)
答:至少需要1.44平方米的铁皮。
(教材第84页“第16题” )
作业课件中的相关练习。
02
01
课后练习题。
课后作业
青岛版数学五年级(上)
五 生活中的多边形
——多边形的面积
平行四边形的面积
S =ɑh
三角形的面积
S =ɑh÷2
梯形的面积
S =(ɑ+b)h÷2
组合图形的面积
转化成求几个简单的平面图形面积的和与差
多边形的面积
知识梳理
需要回顾整理的内容有哪些呢?
推导面积公式时都用了转化的方法。
平方
千米
公顷
平方米
平方
分米
平方
厘米
cm2
dm2
m2
km2
hm2
100
1000000
10000
100
100
“公顷”和“平方米”之间的进率是10000;
其他每相邻两个面积单位之间的进率都是100。
土地面积单位
常用的面积单位
面积单位
要点回顾
1. 回忆下面图形面积计算公式的推导过程,写出计算公式。
平行四边形、三角形和梯形面积计算公式的推导都用到了转化的方法。
a
b
S =
ab
a
h
S =
ah
a
h
S =
ah÷2
b
h
a
S =
(a+b)h÷2
知识点1:面积计算公式的推导
知识点2:面积的计算
2.计算下面图形的面积。
利用字母公式进行计算,先要找到相应的数值,再代入公式计算,最后还要加上单位。
S=ah
=270(cm2)
=18×15
S=ah÷2
=144(cm2)
=36×8÷2
S=a2
=3.61(m2)
=1.9×1.9
计算平行四边形、三角形时,还得注意底和高要相对应。
S=ah÷2
=3.41(m2)
=2.2×3.1÷2
S=ab
=4.5(dm2)
=2.5×1.8
S=(a+b)h÷2
=525(m2)
=(36+14)×21÷2
=50×21÷2
3. (1)两个完全相同的平行四边形(如下图),将图1和图2中阴影部分的面积比较,( ) 。
如图,阴影部分都是三角形,都和平行四边形等底等高,面积都是平行四边形的一半。
A. 图1面积大
B. 图2面积大
D. 无法比较
C. 图1和图2面积一样大
底
高
底
高
C
知识点3:图形间的关系
3. (2)如图,在一组平行线之间有三个图形,下面说法正确的是( )。
平行线之间的距离相等,如果将三个图形的高都假设为10,则三个图形的面积都可以算出来。
A. 三角形面积最大
B. 平行四边形面积最大
D. 三个图形的面积一样大
C. 梯形面积最大
10
5
6
4
D
图形间的面积比较,往往牵涉到图形间的关系:如三角形的面积是与它等底等高的平行四边形面积的一半等。
我们还经常用到如下这些规律:等底等高的平行四边形面积相等;等底等高的三角形面积相等;面积相等的平行四边形、三角形或梯形,形状不一定相同等。
知识点4:组合图形的面积计算
4. 计算右面图形的面积。你能想出几种方法?
组合图形的面积一般有两种思路:①分割法(求和);②添补法(求差)。
方法一:分割成长方形和三角形
S三角形=(10?5)×(12?6)÷2=15(cm2)
S长方形=12×5=60(cm2)
S=15+60=75(cm2)
方法二:分割成长方形和梯形
S长方形=6×5=30(cm2)
S梯形 =(5+10)×(12?6)÷2
=45(cm2)
S=30+45=75(cm2)
方法三:分割成三角形和梯形
S三角形=10×(12?6)÷2 =30(cm2)
S梯形=(6+12)×5÷2=45(cm2)
S=30+45=75(cm2)
方法四:添补成长方形
S长方形=12×10=120(cm2)
S梯形=(6+12)×(10?5)÷2
=45(cm2)
S=120?45=75(cm2)
组合图形的解法往往不止一种,但解题时应综合分析,尽量选用简便的方法计算。
知识点5:土地面积单位的实际应用
5.市政府开展“开荒造林”活动,打算在一块长18千米,
宽6千米的长方形荒地上种树,如果按平均每公顷种
树3500棵计算,大约能种多少棵树?
18×6=108(平方千米)
分析:要求能种多少棵树就要先求出这块地的面积。
3500×10800=3780 0000(棵)
答:大约能种3780 0000棵树。
108平方千米=10800公顷
解决跟面积有关的实际问题要注意单位换算哟!
(1)绿色小麦区的面积是多少平方米?每年可以生产多少千克优质小麦?
360×300=108000(平方米)
108000×0.75=81000(千克)
答:绿色小麦区的面积是108000平方米。每年可以生产81000千克优质小麦。
我学会了吗
(2)蔬菜区辣椒的产值每年约为多少元?
(240+360)×300÷2
=600×300÷2
90000×25=2250000(元)
=90000(平方米)
=180000÷2
答:蔬菜区辣椒的产值每年约为2250000元。
(3)果园占地面积一共是多少平方米?合多少公顷?
120×260÷2+240×120
=15600+28800
=44400(平方米)
=4.44(公顷)
答:果园占地面积一共是444000平方米。合4.44公顷。
(4)你还能提出什么数学问题?
问题:蔬菜区(二)占地面积一共是多少平方米?
240×240=57600(平方米)
答:蔬菜区(二)占地面积一共是57600平方米。
1. 量一量,算一算,求出下面图形的面积。(单位:厘米)
1cm
1.5cm
1.5cm
1.5cm
2.5cm
1.5cm
2.5cm
1cm
1.5cm
2.5cm
2cm
①1×1.5÷2=0.75(cm2)
②2.5×1.5=3.75(cm2)
③1.5×1.5=2.25(cm2)
④2.5×1=2.5(cm2)
⑤(1.5+2.5)×2÷2
=4×2÷2
=4(cm2)
(教材第82页“第1题” )
课堂练习
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}图形
平行四边形
三角形
梯形
底(米)
5.6
底3.上2
下底6.4
高(米)
2.5
7
面积(平方米)
84
43.2
2. 填表。
24
14
9
(教材第82页“第2题” )
3.
这块挡风玻璃的面积大约是多少?
(40+80)×30÷2
=120×30÷2
=1800(平方厘米)
答:这块挡风玻璃的面积大约是1800平方厘米。
(教材第82页“第3题” )
6.5公顷=( )平方米
1200公顷=( )平方千米
48000平方米=( )公顷
305平方分米=( )平方米
2平方分米5平方厘米=( )平方分米
4.填一填。
65000
12
4.8
3.05
2.05
(教材第82页“第4题” )
5.绿化队计划在一块近似平行四边形的空地里栽种一片防护林。如果每8平方米种一棵树,需要多少棵树苗?
120×30÷8=450(棵)
答:需要450棵树苗。
(教材第82页“第5题” )
6.下面是某拦河大坝的横截面示意图。请求出它
的面积。
答:它的面积是2000平方米。
(20+60)×50÷2
=80×50÷2
=2000(平方米)
(教材第82页“第6题” )
7.解方程。
5.2χ=26
χ=5
解:5.2χ÷5.2=26÷5.2
3χ-2.7=12.3
解:3χ-2.7+2.7=12.3+2.7
3χ=15
3χ÷3=15÷3
χ=5
0.6+χ=7.2
解:χ+0.6-0.6=7.2-0.6
χ=6.6
χ÷1.5=8
解:χ÷1.5×1.5=8×1.5
χ=12
(教材第83页“第7题” )
5χ+7χ=84
χ=7
解:12χ=84
12χ÷12=84÷12
3.8χ-0.8χ=4.5
χ=1.5
解:3χ=4.5
3χ÷3=4.5÷3
8. 求出下面图形的面积。
三角形的面积:8×6÷2 = 24(cm?)
平行四边形的面积:10×5 = 50(cm?)
梯形的面积:(6+10)×3÷2 = 24(cm?)
总面积:24+50+24 = 98(cm?)
(教材第83页“第8题” )
长方形的面积:12×5 = 60(cm?)
梯形的面积:(6+4)×3÷2 = 15(cm?)
总面积:60-15 = 45(cm?)
9.一块三角形菜地面积是1公顷。它的高为50米,它的底边长多少米?
1公顷= 10000(m?)
解:设底边是x米。
50χ÷2=10000
χ=400
答:底边长400米。
50χ÷2×2=10000×2
50χ=20000
50χ÷50=20000÷50
(教材第83页“第9题” )
10.在方格纸上画几个已学过的图形,并计算出它们的面积。(每个小方格表示1cm2)
?
长方形的面积:4×3 = 12(cm?)
正方形的面积:5×5 = 25(cm?)
(教材第83页“第10题” )
平行四边形的面积:4×3 = 12(cm?)
三角形的面积:6×4÷2 = 12(cm?)
梯形的面积:(2+8)×4÷2 = 20(cm?)
10.在方格纸上画几个已学过的图形,并计算出它们的面积。(每个小方格表示1cm2)
?
11.如果每平方米摆放20盆花,根据已知的数据,将表格填完整。
200
4000
200
4000
400
8000
(教材第83页“第11题” )
12.求χ的值。
解:设梯形的高是χ米。
10χ÷2 = 20
χ = 4
10χ÷2×2 = 20×2
10χ= 40
10χ÷10= 40÷10
(3+7)χ÷2 = 20
解:设平行四边形的底是χ米。
χ= 8
5χ= 40
5χ÷5= 40÷5
(教材第83页“第12题” )
13.
(1)这片树林一天能释放多少千克氧气?
800×500=400000(平方米)
400000平方米=4公顷
4×750=3000(千克)
答:这片树林一天能释放3000千克氧气。
(教材第84页“第13题” )
(2)这片树林一个月能吸收多少千克二氧化碳?
800×500=400000(平方米)
400000平方米=4公顷
4×950×30=114000(千克)
答:这片树林一个月能吸收114000千克二氧化碳。
13.
(3)你还能提出什么数学问题?
问题:这片树林一周能释放多少千克氧气?
800×500=400000(平方米)
400000平方米=4公顷
4×750×7=21000(千克)
答:这片树林一周能释放21000千克氧气。
13.
650÷(60+70)
=650÷130
=5(小时)
答:火车行驶了5小时。
(教材第84页“第14题” )
14.两列火车同时从滨海站出发,相背而行。开往富江站的火车平均速度为60千米/时,开往双山站的火车平均速度为70千米/时,结果两车正好同时到站。火车行驶了几小时?
15.
如果栽梨树,可以栽多少棵?如果栽苹果树呢?
(30+42)×20÷2
=72×20÷2
=1440÷2
=720(平方米)
梨树:720÷12=60(棵)
苹果树:720÷18=40(棵)
答:如果栽梨树可以栽60棵。如果栽苹果树可以栽40棵。
(教材第84页“第15题” )
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}每棵梨树的占地面积(m?)
12
每棵苹果树的占地面积(m?)
18
左面是一个果园的平面示意图。
做如图所示四个侧面完全相同的抽风机排气口,至少需要多少平方米的铁皮?
16.
(4+8)×6÷2×4
=12×6÷2×4
=144(平方分米)
=1.44(平方米)
答:至少需要1.44平方米的铁皮。
(教材第84页“第16题” )
作业课件中的相关练习。
02
01
课后练习题。
课后作业
