青岛版数学五年级上册 五 生活中的多边形——多边形的面积 信息窗3 梯形的面积 课件(28张ppt)
文档属性
| 名称 | 青岛版数学五年级上册 五 生活中的多边形——多边形的面积 信息窗3 梯形的面积 课件(28张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 00:00:00 | ||
图片预览







文档简介
梯形的面积
青岛版数学五年级(上)
五 生活中的多边形
——多边形的面积
在自主探索、合作交流中经历梯形面积公式的推导过程。
掌握梯形面积的计算方法,并能灵活运用公式解决相关的数学问题。
在探索活动中培养比较和推理能力、发展空间观念。
学习目标
【重点】
理解并掌握梯形的面积计算公式,会计算梯形的面积。
【难点】
自主探究梯形的面积计算公式。
课堂导入
转化法
三角形面积是拼成平行四边形面积的一半。
S=ah
S=ah÷2
旧
新
我们是怎样推导出三角形的面积的计算公式的?
新知探究
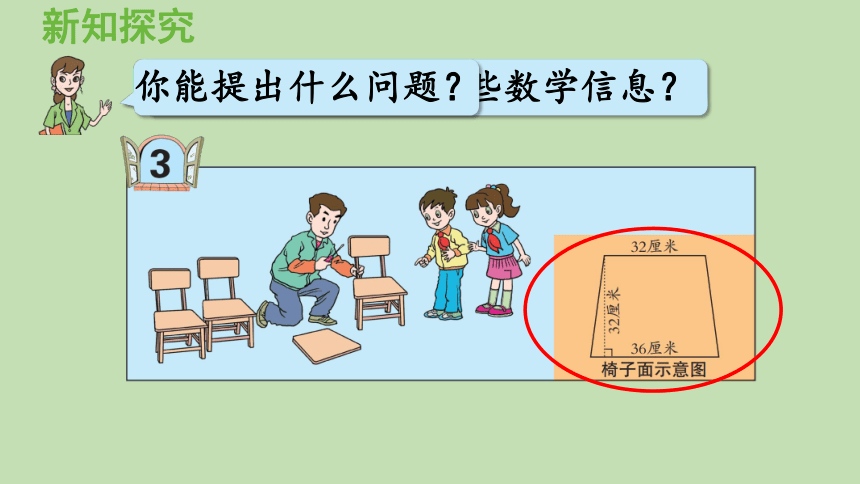
从图中你能获取哪些数学信息?
你能提出什么问题?
椅子面示意图
椅子的面是梯形的。想一想:怎样求梯形的面积呢?
类比三角形,猜一猜,看能把梯形转化成你学过的什么图形?
制作这个椅子面需要多少平方厘米的木材?
我们可以借助学具来研究。
高
上底
下底
上底×高÷2
把一个梯形分割成两个三角形。
(上底+下底)
下底×高÷2
+
÷2
×高
=
梯形的面积
两个三角形的面积之和
=
=
高
情况一
上底
下底
上底
梯形的面积=
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
大三角形的面积
把一个梯形割补成一个大三角形。
高
情况二
高÷2
上底+下底
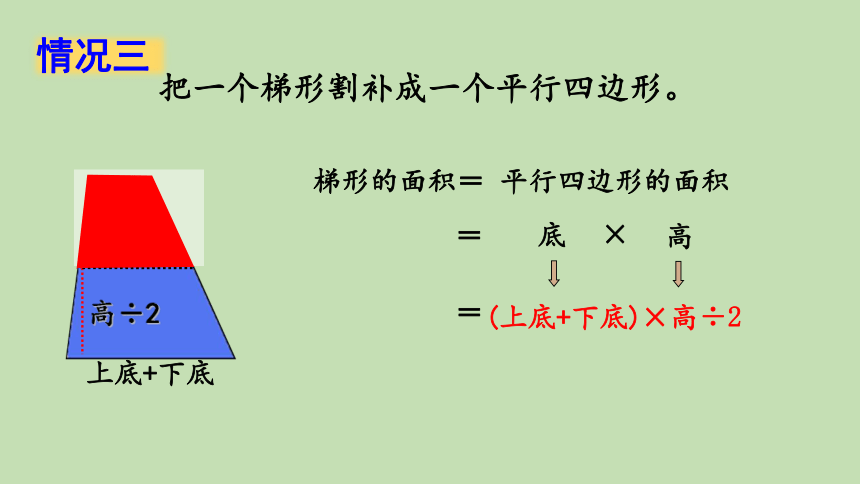
梯形的面积= 平行四边形的面积
=
底
×
高
(上底+下底)
÷2
×高
=
把一个梯形割补成一个平行四边形。
情况三
把两个完全相同的梯形拼成一平行四边形。
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
下底
上底
高
下底
上底
梯形的面积= (上底+下底)×高÷2
情况四
梯形的面积 = (上底+下底)×高÷2
用字母表示:S=(a+b)×h÷2
????
?
????
?
S = (a+b)h÷2
????
?
如果用 S 表示梯形的面积,用 a、b 和 h 分别
表示梯形的上底、下底和高,那么梯形的面积
计算公式是:
(32+36)×32÷2
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
制作这个椅子面需要多少平方厘米的木材?
椅子面示意图
错误解答
计算右面图形的面积。
(18+9)×10
=27×10
=270(dm2)
易错提醒
错因分析:
梯形的面积计算公式记错。忘记÷2。
正确解答
(18+9)×10÷2
=27×10÷2
=135(dm2)
1.计算下面图形的面积。
(17+23)×15÷2
=40×15÷2
=300(m2)
(18+9)×10÷2
=27×10÷2
=135(dm2)
(42+26)×30÷2
=68×30÷2
=1020(cm2)
课堂练习
(教材第74页“第1题” )
3
3
3
6
6
6
7
(3+6)×7÷2
= 9×7÷2
= 31.5(c㎡)
我发现:等底等高的梯形面积一定相等。
2.计算下面每个梯形的面积,你发现了什么?(单位:cm)
(8+5)×1.8÷2
3.某水渠的横截面是梯形(如图)渠口宽8米。渠底5米,渠深1.8米。求它的横截面面积。
= 13×1.8÷2
= 11.7(平方米)
答:它的横截面是11.7平方米。
(教材第74页“第2题” )
4.
(40+60)×30÷2 ×10
= 100×30÷2×10
= 15000(cm2)
做10件这样的围裙,大约用多少平方米布?
答:做10件这样的围裙,大约用1.5平方米布。
15000cm2=1.5m2
(教材第74页“第3题” )
5.量一量,算一算,求出下面图形的面积。
2cm
4cm
2cm
2cm
3.5cm
2.5cm
(2+4)×2÷2
= 6×2÷2
= 6(cm2)
(3.5+2.5)×2÷2
= 6×2÷2
= 6(cm2)
(教材第74页“第4题” )
6. 已知一个梯形的面积是15cm2。它的上底是4.5cm,高是3cm,下底是多少厘米?(列方程解决。)
解:
设下底是xcm。
(4.5+x)×3÷2=15
4.5+x=15×2÷3
4.5+x=10
x=10?4.5
x=5.5
答:
下底是5.5cm。
3cm
上底4.5cm
xcm
7. 木材场常常把木材堆成下图形状。在计算木材根数时通常用下面的方法:
(顶层根数+底层根数)×层数÷2
(1)请算出图中木材的根数。
(2)你能用梯形面积公式解释上面的算法吗?
(教材第75页“第5题” )
(教材第75页“第5题” )
(顶层根数+底层根数)×层数÷2
3根
6根
3根
6根
3+6=9
4+5=9
5+4=9
6+3=9
圆木的总根数×2 =
每层的根数 × 层数
圆木的总根数 =
(3+6)×4÷2= 18(根)
答:这堆木材共有 18 根。
8.
(教材第75页“第6题” )
下底:
84-(19+24)=41(米)
面积:
S=(a+b)×h÷2
=(19+41)×24÷2
=60×24÷2
=60×12
=720(平方米)
9.
(教材第75页“第6题” )
①算出三角形的高
=60×2÷15
=8(m)
h=2S÷a
②算出梯形的面积
S=(a+b)×h÷2
=(5+15)×8÷2
=20×8÷2
=20×4
=80(m2)
10.把下面图形分别分成3个面积相等的图形,可以怎样分?
(教材第75页“第7题” )
※11.在方格纸上画出面积是6平方厘米、形状不同的梯形, 并计算验证。
1cm2
(2+4)×2÷2
=6×2÷2
= 6(cm2)
(1+2)×4÷2
=3×4÷2
= 6(cm2)
(1+5)×2÷2
=6×2÷2
= 6(cm2)
(1+3)×3÷2
=4×3÷2
= 6(cm2)
课堂小结
梯形的面积=(上底+下底)×高÷2
用字母表示:S=(a+b)h÷2
想一想:怎样计算梯形的面积?
两个( )的梯形可以拼成一个平行四边形。这个平行四边形的底等于梯形的( )与( )的和,高等于梯形的( ),每个梯形的面积等于拼成的平行四边形面积的( )。
梯形面积用字母表示为( )。
完全一样
上底
下底
高
一半
S=(a+b)×h÷2
作业课件中的相关练习。
02
01
课后练习题。
课后作业
青岛版数学五年级(上)
五 生活中的多边形
——多边形的面积
在自主探索、合作交流中经历梯形面积公式的推导过程。
掌握梯形面积的计算方法,并能灵活运用公式解决相关的数学问题。
在探索活动中培养比较和推理能力、发展空间观念。
学习目标
【重点】
理解并掌握梯形的面积计算公式,会计算梯形的面积。
【难点】
自主探究梯形的面积计算公式。
课堂导入
转化法
三角形面积是拼成平行四边形面积的一半。
S=ah
S=ah÷2
旧
新
我们是怎样推导出三角形的面积的计算公式的?
新知探究
从图中你能获取哪些数学信息?
你能提出什么问题?
椅子面示意图
椅子的面是梯形的。想一想:怎样求梯形的面积呢?
类比三角形,猜一猜,看能把梯形转化成你学过的什么图形?
制作这个椅子面需要多少平方厘米的木材?
我们可以借助学具来研究。
高
上底
下底
上底×高÷2
把一个梯形分割成两个三角形。
(上底+下底)
下底×高÷2
+
÷2
×高
=
梯形的面积
两个三角形的面积之和
=
=
高
情况一
上底
下底
上底
梯形的面积=
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
大三角形的面积
把一个梯形割补成一个大三角形。
高
情况二
高÷2
上底+下底
梯形的面积= 平行四边形的面积
=
底
×
高
(上底+下底)
÷2
×高
=
把一个梯形割补成一个平行四边形。
情况三
把两个完全相同的梯形拼成一平行四边形。
梯形的面积
÷
2
平行四边形的面积
=
底
×
高
(上底+下底)
×
=
2
高
÷
÷
2
=
下底
上底
高
下底
上底
梯形的面积= (上底+下底)×高÷2
情况四
梯形的面积 = (上底+下底)×高÷2
用字母表示:S=(a+b)×h÷2
????
?
????
?
S = (a+b)h÷2
????
?
如果用 S 表示梯形的面积,用 a、b 和 h 分别
表示梯形的上底、下底和高,那么梯形的面积
计算公式是:
(32+36)×32÷2
=68×32÷2
=2176÷2
=1088(平方厘米)
答:制作这个椅子面需要1088平方厘米的木材。
制作这个椅子面需要多少平方厘米的木材?
椅子面示意图
错误解答
计算右面图形的面积。
(18+9)×10
=27×10
=270(dm2)
易错提醒
错因分析:
梯形的面积计算公式记错。忘记÷2。
正确解答
(18+9)×10÷2
=27×10÷2
=135(dm2)
1.计算下面图形的面积。
(17+23)×15÷2
=40×15÷2
=300(m2)
(18+9)×10÷2
=27×10÷2
=135(dm2)
(42+26)×30÷2
=68×30÷2
=1020(cm2)
课堂练习
(教材第74页“第1题” )
3
3
3
6
6
6
7
(3+6)×7÷2
= 9×7÷2
= 31.5(c㎡)
我发现:等底等高的梯形面积一定相等。
2.计算下面每个梯形的面积,你发现了什么?(单位:cm)
(8+5)×1.8÷2
3.某水渠的横截面是梯形(如图)渠口宽8米。渠底5米,渠深1.8米。求它的横截面面积。
= 13×1.8÷2
= 11.7(平方米)
答:它的横截面是11.7平方米。
(教材第74页“第2题” )
4.
(40+60)×30÷2 ×10
= 100×30÷2×10
= 15000(cm2)
做10件这样的围裙,大约用多少平方米布?
答:做10件这样的围裙,大约用1.5平方米布。
15000cm2=1.5m2
(教材第74页“第3题” )
5.量一量,算一算,求出下面图形的面积。
2cm
4cm
2cm
2cm
3.5cm
2.5cm
(2+4)×2÷2
= 6×2÷2
= 6(cm2)
(3.5+2.5)×2÷2
= 6×2÷2
= 6(cm2)
(教材第74页“第4题” )
6. 已知一个梯形的面积是15cm2。它的上底是4.5cm,高是3cm,下底是多少厘米?(列方程解决。)
解:
设下底是xcm。
(4.5+x)×3÷2=15
4.5+x=15×2÷3
4.5+x=10
x=10?4.5
x=5.5
答:
下底是5.5cm。
3cm
上底4.5cm
xcm
7. 木材场常常把木材堆成下图形状。在计算木材根数时通常用下面的方法:
(顶层根数+底层根数)×层数÷2
(1)请算出图中木材的根数。
(2)你能用梯形面积公式解释上面的算法吗?
(教材第75页“第5题” )
(教材第75页“第5题” )
(顶层根数+底层根数)×层数÷2
3根
6根
3根
6根
3+6=9
4+5=9
5+4=9
6+3=9
圆木的总根数×2 =
每层的根数 × 层数
圆木的总根数 =
(3+6)×4÷2= 18(根)
答:这堆木材共有 18 根。
8.
(教材第75页“第6题” )
下底:
84-(19+24)=41(米)
面积:
S=(a+b)×h÷2
=(19+41)×24÷2
=60×24÷2
=60×12
=720(平方米)
9.
(教材第75页“第6题” )
①算出三角形的高
=60×2÷15
=8(m)
h=2S÷a
②算出梯形的面积
S=(a+b)×h÷2
=(5+15)×8÷2
=20×8÷2
=20×4
=80(m2)
10.把下面图形分别分成3个面积相等的图形,可以怎样分?
(教材第75页“第7题” )
※11.在方格纸上画出面积是6平方厘米、形状不同的梯形, 并计算验证。
1cm2
(2+4)×2÷2
=6×2÷2
= 6(cm2)
(1+2)×4÷2
=3×4÷2
= 6(cm2)
(1+5)×2÷2
=6×2÷2
= 6(cm2)
(1+3)×3÷2
=4×3÷2
= 6(cm2)
课堂小结
梯形的面积=(上底+下底)×高÷2
用字母表示:S=(a+b)h÷2
想一想:怎样计算梯形的面积?
两个( )的梯形可以拼成一个平行四边形。这个平行四边形的底等于梯形的( )与( )的和,高等于梯形的( ),每个梯形的面积等于拼成的平行四边形面积的( )。
梯形面积用字母表示为( )。
完全一样
上底
下底
高
一半
S=(a+b)×h÷2
作业课件中的相关练习。
02
01
课后练习题。
课后作业
