青岛版数学五年级上册 五 生活中的多边形——多边形的面积 信息窗4 组合图形的面积 课件(30张ppt)
文档属性
| 名称 | 青岛版数学五年级上册 五 生活中的多边形——多边形的面积 信息窗4 组合图形的面积 课件(30张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 13:46:38 | ||
图片预览








文档简介
组合图形的面积
青岛版数学五年级(上)
五 生活中的多边形
——多边形的面积
1. 结合生活实际认识组合图形,会把组合图形分解成学过的平面图形并计算出面积。
2. 通过找一找、分一分、拼一拼,培养识图的能力和综合运用有关知识的能力,能合理地运用“割”“补”等方法来计算组合图形的面积。
3. 能运用所学知识,解决生活中组合图形的实际问题。培养合作、探索意识以及创新精神,养成积极参与数学学习活动的好习惯。
学习目标
【重点】
探索并掌握组合图形的面积计算方法。
【难点】
理解并掌握组合图形的组合及分解方法。
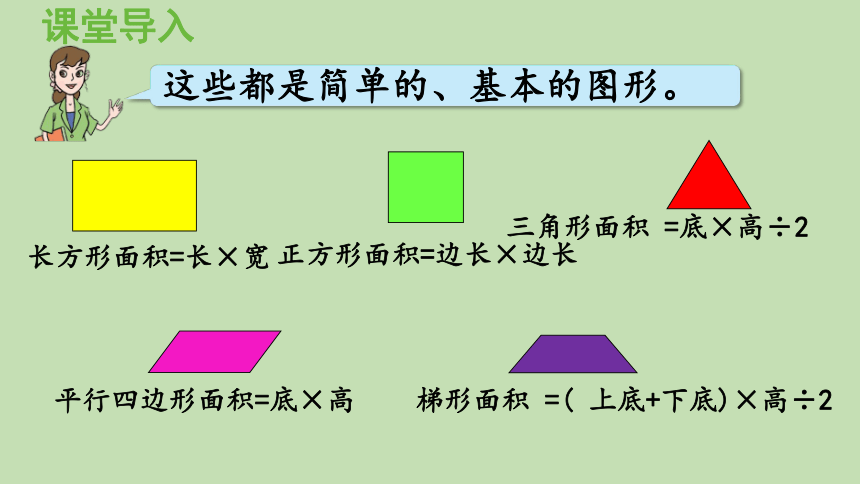
长方形面积=长×宽
正方形面积=边长×边长
三角形面积 =底×高÷2
平行四边形面积=底×高
梯形面积 =( 上底+下底)×高÷2
课堂导入
这些都是简单的、基本的图形。
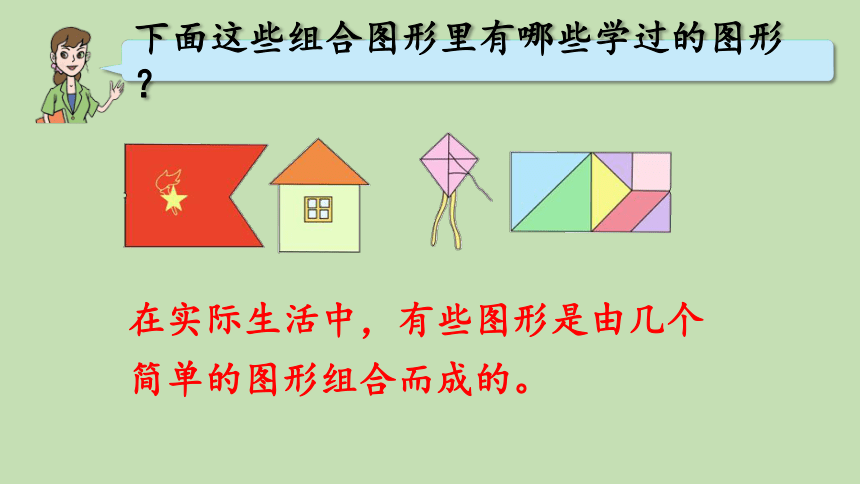
在实际生活中,有些图形是由几个简单的图形组合而成的。
下面这些组合图形里有哪些学过的图形?
新知探究
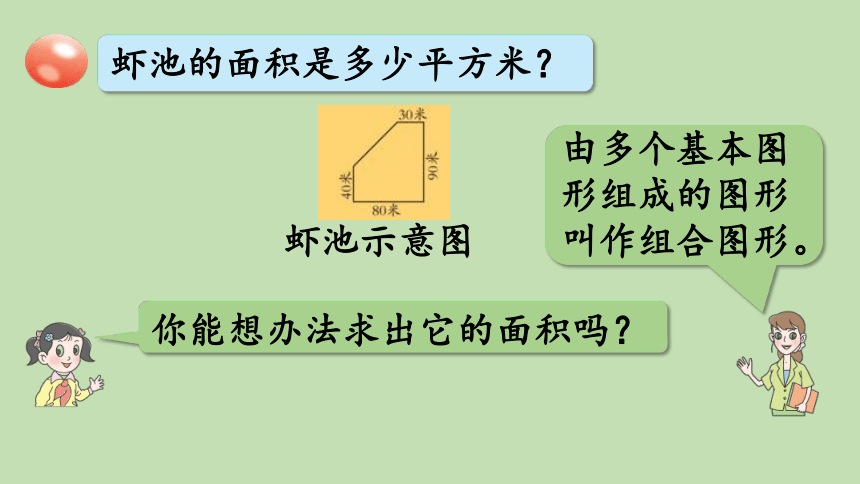
从图中你能获取哪些数学信息?
你能提出什么问题?
虾池示意图
由多个基本图形组成的图形叫作组合图形。
你能想办法求出它的面积吗?
虾池的面积是多少平方米?
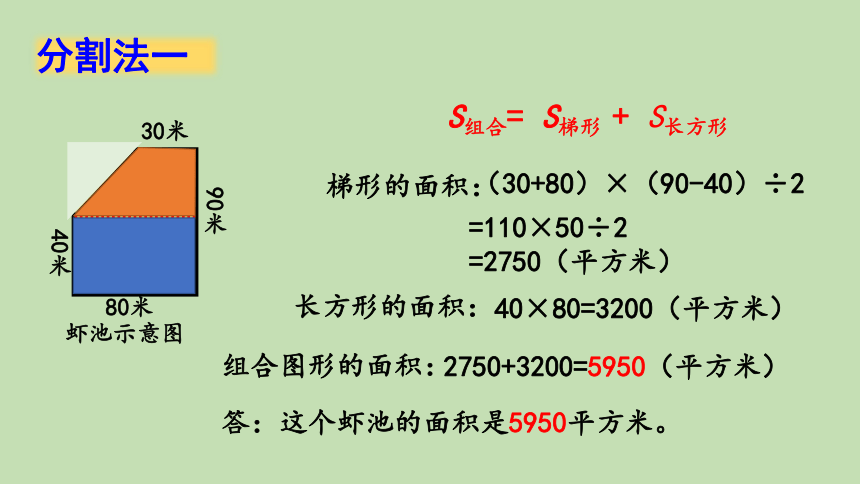
40×80=3200(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
80米
30米
40米
90米
虾池示意图
=110×50÷2
梯形的面积:
(30+80)×(90-40)÷2
=2750(平方米)
长方形的面积:
组合图形的面积:
2750+3200=5950(平方米)
分割法一
80 米
30 米
40 米
90 米
虾池示意图
90×30=2700(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
=130×(80-30)÷2
梯形的面积:
(40+90)×(80-30)÷2
=3250(平方米)
长方形的面积:
组合图形的面积:
3250+2700=5950(平方米)
分割法二
40×80=3200(平方米)
答:这个虾池的面积是5950平方米。
=30×50
长方形的面积:
30×(90-40)
=1500(平方米)
长方形的面积:
组合图形的面积:
1250+1500+3200=5950(平方米)
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
分割法三
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
长方形的面积:
长方形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
30×90=2700(平方米)
40×(80-30)=2000(平方米)
组合图形的面积:
1250+2700+2000=5950(平方米)
答:这个虾池的面积是5950平方米。
分割法四
S组合图形=S长方形 - S三角形
80 米
30 米
40 米
90 米
虾池示意图
90×80=7200(平方米)
答:这个虾池的面积是5950平方米。
长方形的面积:
组合图形的面积:
7200-1250=5950(平方米)
三角形的面积:
(90-40)×(80-30)÷2
=50×50÷2
=1250(平方米)
添补法
S组合图形 = S平行四边形+ S长方形
= 480(平方厘米)
15×12 - 5×5
S组合图形 = S长方形-S正方形
= 155(平方分米)
= 180 - 25
添补法
分割法
30×6 +30×10
= 180 +300
你会求下面图形的面积吗?
S组合图形 = S梯形 + S三角形
(24+36)×8÷2 + 36×30÷2
= 780(cm2)
= 60×8÷2 + 1080÷2
= 240 + 540
分割法
你会求下面图形的面积吗?
求组合图形面积的一般方法:
⑴分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
⑵添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
1. 求下面图形的面积。
课堂练习
(教材第77页“第1题” )
S组合图形 = S长方形-S三角形
8×12-8×7÷2=68(dm2)
S组合图形 = S正方形 + S梯形
8×8+(8+12)×4÷2=104(cm2)
2.有一块五边形的沙发巾(如右图),制作这样一个沙发巾需要多少平方厘米的布料?
S组合图形=S长方形 + S三角形
60×40+60×40÷2
= 2400+1200
= 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料。
(教材第77页“第2题” )
3. 求下面图形的面积。
(教材第78页“第3题” )
S组合图形 = S长方形 + 2×S正方形
6×3+2×2×2=26(cm2)
S组合图形 = S梯形 + 2×S三角形
(7+10)×8÷2+2×5×10÷2=118(cm2)
4. 学校举办歌咏比赛,要制作一些锦旗(样式如右图)。做12面锦旗需要多少平方厘米布?
S组合图形 = S长方形 - S三角形
12×(60×30-30×15÷2)= 18900(cm2)
答:需要 18900 平方厘米的布。
(教材第78页“第4题” )
5. 下面图形的面积各是多少?(单位:cm)。
(教材第78页“第5题” )
S组合图形 = S长方形 - S长方形
26×36-16×26=520(cm2)
S组合图形 = S正方形 -2× S三角形
30×30-2×10×12÷2=780(cm2)
6.草坪占地多少平方米?
S组合图形 = S梯形 - S长方形
= 54 - 6
= 48(平方米)
(8+10)×6÷2 - 3×2
= 18×6÷2 - 6
答:草坪占地48平方米。
(教材第78页“第6题” )
7.小明家一面外墙墙皮脱落,要重新粉刷(如图),每平方米需要用0.5千克涂料。如果涂料的价钱是每千克10 元,粉刷这面墙需要多少钱?
= 36(平方米)
8×2÷2 + 8×3.5
= 8 + 28
答:粉刷这面墙需要180元钱。
S组合图形 = S三角形 + S长方形
36×0.5×10 = 180(元)
(教材第78页“第7题” )
从整体来看,阴影部分面积 =大正方形面积+小正方形面积-空白三角形面积-空白梯形面积。
8.求右图中阴影部分的面积。(单位:cm)
6
6
3
3
大正方形:6×6 = 36(cm2)
小正方形:3×3 = 9(cm2)
空白三角形:3×3÷2 =4.5(cm2)
空白梯形: (6-3+6)×6÷2 =27(cm2)
阴影部分:36+9-4.5-27 = 13.5(cm2)
答:阴影部分的面积是13.5cm2 。
方法一
如果只看阴影部分,则可以把它分成两个小三角形;或直接把它看作一个梯形。
6
6
3
3
梯形:(3+6)×3÷2 =13.5(cm2)
答:阴影部分的面积是13.5cm2 。
阴影小三角形:3×3÷2= 4.5(cm2)
阴影大三角形:6×3÷2 =9(cm2)
阴影部分:4.5+9 = 13.5(cm2)
答:阴影部分的面积是13.5cm2 。
方法二
方法三
想一想:怎样计算组合图形的面积?
分割法
添补法
转化成基本图形
课堂小结
计算组合图形的面积,要看清图形组合的特点,再确定用哪种方法计算。如果有多种解法时,要善于多中选优,选择最简便的方法。
作业课件中的相关练习。
02
01
课后练习题。
课后作业
青岛版数学五年级(上)
五 生活中的多边形
——多边形的面积
1. 结合生活实际认识组合图形,会把组合图形分解成学过的平面图形并计算出面积。
2. 通过找一找、分一分、拼一拼,培养识图的能力和综合运用有关知识的能力,能合理地运用“割”“补”等方法来计算组合图形的面积。
3. 能运用所学知识,解决生活中组合图形的实际问题。培养合作、探索意识以及创新精神,养成积极参与数学学习活动的好习惯。
学习目标
【重点】
探索并掌握组合图形的面积计算方法。
【难点】
理解并掌握组合图形的组合及分解方法。
长方形面积=长×宽
正方形面积=边长×边长
三角形面积 =底×高÷2
平行四边形面积=底×高
梯形面积 =( 上底+下底)×高÷2
课堂导入
这些都是简单的、基本的图形。
在实际生活中,有些图形是由几个简单的图形组合而成的。
下面这些组合图形里有哪些学过的图形?
新知探究
从图中你能获取哪些数学信息?
你能提出什么问题?
虾池示意图
由多个基本图形组成的图形叫作组合图形。
你能想办法求出它的面积吗?
虾池的面积是多少平方米?
40×80=3200(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
80米
30米
40米
90米
虾池示意图
=110×50÷2
梯形的面积:
(30+80)×(90-40)÷2
=2750(平方米)
长方形的面积:
组合图形的面积:
2750+3200=5950(平方米)
分割法一
80 米
30 米
40 米
90 米
虾池示意图
90×30=2700(平方米)
S组合= S梯形 + S长方形
答:这个虾池的面积是5950平方米。
=130×(80-30)÷2
梯形的面积:
(40+90)×(80-30)÷2
=3250(平方米)
长方形的面积:
组合图形的面积:
3250+2700=5950(平方米)
分割法二
40×80=3200(平方米)
答:这个虾池的面积是5950平方米。
=30×50
长方形的面积:
30×(90-40)
=1500(平方米)
长方形的面积:
组合图形的面积:
1250+1500+3200=5950(平方米)
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
分割法三
80米
30米
40米
90米
虾池示意图
S组合= S三角形 + S长方形+ S长方形
三角形的面积:
长方形的面积:
长方形的面积:
(80-30)×(90-40)÷2
=50×50÷2
=1250(平方米)
30×90=2700(平方米)
40×(80-30)=2000(平方米)
组合图形的面积:
1250+2700+2000=5950(平方米)
答:这个虾池的面积是5950平方米。
分割法四
S组合图形=S长方形 - S三角形
80 米
30 米
40 米
90 米
虾池示意图
90×80=7200(平方米)
答:这个虾池的面积是5950平方米。
长方形的面积:
组合图形的面积:
7200-1250=5950(平方米)
三角形的面积:
(90-40)×(80-30)÷2
=50×50÷2
=1250(平方米)
添补法
S组合图形 = S平行四边形+ S长方形
= 480(平方厘米)
15×12 - 5×5
S组合图形 = S长方形-S正方形
= 155(平方分米)
= 180 - 25
添补法
分割法
30×6 +30×10
= 180 +300
你会求下面图形的面积吗?
S组合图形 = S梯形 + S三角形
(24+36)×8÷2 + 36×30÷2
= 780(cm2)
= 60×8÷2 + 1080÷2
= 240 + 540
分割法
你会求下面图形的面积吗?
求组合图形面积的一般方法:
⑴分割法:可以把一个组合图形分成几个简单的图形,分别求出这几个简单图形的面积,再求和。
⑵添补法:可以把一个组合图形看作是从一个简单图形中减去几个简单的图形,求出它们的面积差。
1. 求下面图形的面积。
课堂练习
(教材第77页“第1题” )
S组合图形 = S长方形-S三角形
8×12-8×7÷2=68(dm2)
S组合图形 = S正方形 + S梯形
8×8+(8+12)×4÷2=104(cm2)
2.有一块五边形的沙发巾(如右图),制作这样一个沙发巾需要多少平方厘米的布料?
S组合图形=S长方形 + S三角形
60×40+60×40÷2
= 2400+1200
= 3600(cm2)
答:制作这样一个沙发巾需要3600平方厘米的布料。
(教材第77页“第2题” )
3. 求下面图形的面积。
(教材第78页“第3题” )
S组合图形 = S长方形 + 2×S正方形
6×3+2×2×2=26(cm2)
S组合图形 = S梯形 + 2×S三角形
(7+10)×8÷2+2×5×10÷2=118(cm2)
4. 学校举办歌咏比赛,要制作一些锦旗(样式如右图)。做12面锦旗需要多少平方厘米布?
S组合图形 = S长方形 - S三角形
12×(60×30-30×15÷2)= 18900(cm2)
答:需要 18900 平方厘米的布。
(教材第78页“第4题” )
5. 下面图形的面积各是多少?(单位:cm)。
(教材第78页“第5题” )
S组合图形 = S长方形 - S长方形
26×36-16×26=520(cm2)
S组合图形 = S正方形 -2× S三角形
30×30-2×10×12÷2=780(cm2)
6.草坪占地多少平方米?
S组合图形 = S梯形 - S长方形
= 54 - 6
= 48(平方米)
(8+10)×6÷2 - 3×2
= 18×6÷2 - 6
答:草坪占地48平方米。
(教材第78页“第6题” )
7.小明家一面外墙墙皮脱落,要重新粉刷(如图),每平方米需要用0.5千克涂料。如果涂料的价钱是每千克10 元,粉刷这面墙需要多少钱?
= 36(平方米)
8×2÷2 + 8×3.5
= 8 + 28
答:粉刷这面墙需要180元钱。
S组合图形 = S三角形 + S长方形
36×0.5×10 = 180(元)
(教材第78页“第7题” )
从整体来看,阴影部分面积 =大正方形面积+小正方形面积-空白三角形面积-空白梯形面积。
8.求右图中阴影部分的面积。(单位:cm)
6
6
3
3
大正方形:6×6 = 36(cm2)
小正方形:3×3 = 9(cm2)
空白三角形:3×3÷2 =4.5(cm2)
空白梯形: (6-3+6)×6÷2 =27(cm2)
阴影部分:36+9-4.5-27 = 13.5(cm2)
答:阴影部分的面积是13.5cm2 。
方法一
如果只看阴影部分,则可以把它分成两个小三角形;或直接把它看作一个梯形。
6
6
3
3
梯形:(3+6)×3÷2 =13.5(cm2)
答:阴影部分的面积是13.5cm2 。
阴影小三角形:3×3÷2= 4.5(cm2)
阴影大三角形:6×3÷2 =9(cm2)
阴影部分:4.5+9 = 13.5(cm2)
答:阴影部分的面积是13.5cm2 。
方法二
方法三
想一想:怎样计算组合图形的面积?
分割法
添补法
转化成基本图形
课堂小结
计算组合图形的面积,要看清图形组合的特点,再确定用哪种方法计算。如果有多种解法时,要善于多中选优,选择最简便的方法。
作业课件中的相关练习。
02
01
课后练习题。
课后作业
