青岛版数学五年级上册 七 绿色家园——折线统计图 智慧广场 课件(19张ppt)
文档属性
| 名称 | 青岛版数学五年级上册 七 绿色家园——折线统计图 智慧广场 课件(19张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 13:55:49 | ||
图片预览






文档简介
智慧广场
青岛版数学五年级(上)
七 绿色家园
——折线统计图
利用已有经验认识和了解简单的?“?排列?”问题?。
掌握解决问题的策略和方法,体会解决问题策略的多样性。
培养初步的观察、分析及推理能力?,?能有序地、全面地思考问题。
活动目标
课堂导入
同学没,你注意到下面的密码是如何排列的吗?
从图中你能获取哪些数学信息?
拍照中有什么数学问题吗?
新知探究
有多少种不同的排法?
小冬、小华、小平3个同学排成一行照相。
小冬
小华
小平
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
有4种排法:
她说得对吗?这样排列有没有遗漏?
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小平
小华
小冬
小华
小平
小冬
小平
小冬
小华
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
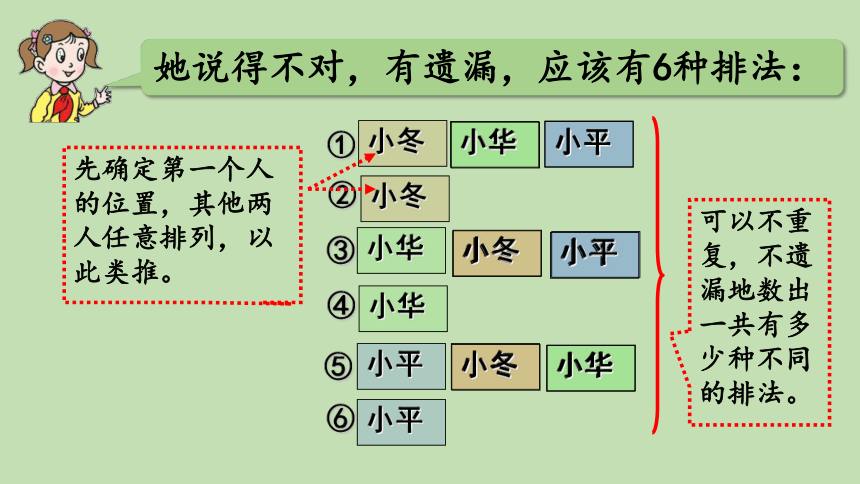
她说得不对,有遗漏,应该有6种排法:
小冬
小华
小平
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
还可以用图形代表人物来摆一摆。
用不同的图形代替不同的人,既直观,又简洁。
A
B
C
A
B
C
B
C
A
C
B
A
B
C
A
C
A
B
①
②
③
④
⑤
⑥
小冬
A
小华
B
小平
C
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
还可以用字母代表人物来摆一摆。
用不同的字母代替不同的人,既然简洁,又可以表示任意3种物体的直线排列方法。
先确定第一个人的位置,其他两人自由排列,数出有几种排列方法,依次类推,这样可以不重复、不遗漏地数出一共有多少种排法。
1.3个同学排成一行跳舞,可以有多少种不同的排法?
② 小云 小雪 小雨
① 小云 小雨 小雪
④ 小雨 小云 小雪
③ 小雨 小雪 小云
⑤ 小雪 小雨 小云
⑥ 小雪 小云 小雨
课堂练习
(教材第114页“第1题” )
6种。
2.用红、眼、花三个字能组成几个词语?
6个
红
眼
花
红眼
红花
眼
红
眼红
花
眼花
花
眼
红
花眼
花红
3. 用下面的文字卡片,你能摆出多少个由 3 个字组成的短句?
① 龙虎斗
② 龙斗虎
③ 虎龙斗
④ 虎斗龙
⑤ 斗龙虎
⑥ 斗虎龙
(教材第114页“第2题” )
6个
4. 要在酒店大门的上方挂 6 只大灯笼(如图),如果把形状相同的灯笼挨在一起,可以有多少种不同的挂法?
△△□□○○
△△○○□□
□□△△○○
□□○○△△
○○□□△△
○○△△□□
(教材第114页“第3题” )
6种
△
□
○
5. 4位同学排一行表演小合唱,丁刚同学担任领唱,固定在左起第二个位置上,其余同学任意排。有多少种不同的排法?
ABCD
ABDC
CBAD
CBDA
DBCA
DBAC
(教材第114页“第4题” )
A
B
C
D
6种
6. 五年级一班在筹划参加校运动会接力赛方案时,决定让本班短跑速度最快的王明同学跑最后一棒,其余三名同学李华、张强、丁力跑其他三棒。可以有多少种不同的安排方法?
(教材第114页“第5题” )
A:李华
B:张强
C:丁力
D:王明
ABCD
ACBD
BACD
BCAD
CBAD
CABD
6种
7.用0?3四张数字卡片可以组成多少个不同的四位数?
1023 1032 1203 1230 1302 1320
6个
2013 2031 2103 2130 2301 2310
6个
3012 3021 3102 3120 3201 3210
6个
答:可以组成 18 个不同的四位数。
(教材第114页“第6题” )
注意0不能放在最高位上。
想一想:怎样解决简单的排列问题?
方法:先确定进行排列的第一个排列的位置,其他的自由排列,数出有几种排列方法,依次类推,这样可以不重复、不遗漏地数出一共有多少种排法。
策略:用字母或数字代替具体的事物,会使排列问题变得更加简单。
课堂小结
课后作业
作业课件中的相关练习。
02
01
课后练习。
青岛版数学五年级(上)
七 绿色家园
——折线统计图
利用已有经验认识和了解简单的?“?排列?”问题?。
掌握解决问题的策略和方法,体会解决问题策略的多样性。
培养初步的观察、分析及推理能力?,?能有序地、全面地思考问题。
活动目标
课堂导入
同学没,你注意到下面的密码是如何排列的吗?
从图中你能获取哪些数学信息?
拍照中有什么数学问题吗?
新知探究
有多少种不同的排法?
小冬、小华、小平3个同学排成一行照相。
小冬
小华
小平
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小冬
小平
小华
①
②
③
④
有4种排法:
她说得对吗?这样排列有没有遗漏?
小冬
小华
小平
小冬
小华
小平
小华
小平
小冬
小平
小华
小冬
小华
小平
小冬
小平
小冬
小华
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
她说得不对,有遗漏,应该有6种排法:
小冬
小华
小平
①
②
③
④
⑤
⑥
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
还可以用图形代表人物来摆一摆。
用不同的图形代替不同的人,既直观,又简洁。
A
B
C
A
B
C
B
C
A
C
B
A
B
C
A
C
A
B
①
②
③
④
⑤
⑥
小冬
A
小华
B
小平
C
可以不重复,不遗漏地数出一共有多少种不同的排法。
先确定第一个人的位置,其他两人任意排列,以此类推。
还可以用字母代表人物来摆一摆。
用不同的字母代替不同的人,既然简洁,又可以表示任意3种物体的直线排列方法。
先确定第一个人的位置,其他两人自由排列,数出有几种排列方法,依次类推,这样可以不重复、不遗漏地数出一共有多少种排法。
1.3个同学排成一行跳舞,可以有多少种不同的排法?
② 小云 小雪 小雨
① 小云 小雨 小雪
④ 小雨 小云 小雪
③ 小雨 小雪 小云
⑤ 小雪 小雨 小云
⑥ 小雪 小云 小雨
课堂练习
(教材第114页“第1题” )
6种。
2.用红、眼、花三个字能组成几个词语?
6个
红
眼
花
红眼
红花
眼
红
眼红
花
眼花
花
眼
红
花眼
花红
3. 用下面的文字卡片,你能摆出多少个由 3 个字组成的短句?
① 龙虎斗
② 龙斗虎
③ 虎龙斗
④ 虎斗龙
⑤ 斗龙虎
⑥ 斗虎龙
(教材第114页“第2题” )
6个
4. 要在酒店大门的上方挂 6 只大灯笼(如图),如果把形状相同的灯笼挨在一起,可以有多少种不同的挂法?
△△□□○○
△△○○□□
□□△△○○
□□○○△△
○○□□△△
○○△△□□
(教材第114页“第3题” )
6种
△
□
○
5. 4位同学排一行表演小合唱,丁刚同学担任领唱,固定在左起第二个位置上,其余同学任意排。有多少种不同的排法?
ABCD
ABDC
CBAD
CBDA
DBCA
DBAC
(教材第114页“第4题” )
A
B
C
D
6种
6. 五年级一班在筹划参加校运动会接力赛方案时,决定让本班短跑速度最快的王明同学跑最后一棒,其余三名同学李华、张强、丁力跑其他三棒。可以有多少种不同的安排方法?
(教材第114页“第5题” )
A:李华
B:张强
C:丁力
D:王明
ABCD
ACBD
BACD
BCAD
CBAD
CABD
6种
7.用0?3四张数字卡片可以组成多少个不同的四位数?
1023 1032 1203 1230 1302 1320
6个
2013 2031 2103 2130 2301 2310
6个
3012 3021 3102 3120 3201 3210
6个
答:可以组成 18 个不同的四位数。
(教材第114页“第6题” )
注意0不能放在最高位上。
想一想:怎样解决简单的排列问题?
方法:先确定进行排列的第一个排列的位置,其他的自由排列,数出有几种排列方法,依次类推,这样可以不重复、不遗漏地数出一共有多少种排法。
策略:用字母或数字代替具体的事物,会使排列问题变得更加简单。
课堂小结
课后作业
作业课件中的相关练习。
02
01
课后练习。
