沪科版八年级上册数学课件-14.2.4 用AAS判定三角形全等(15张PPT)
文档属性
| 名称 | 沪科版八年级上册数学课件-14.2.4 用AAS判定三角形全等(15张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 445.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-04 22:40:11 | ||
图片预览



文档简介
第4课时 用AAS判定三角形全等
沪科版·八年级上册
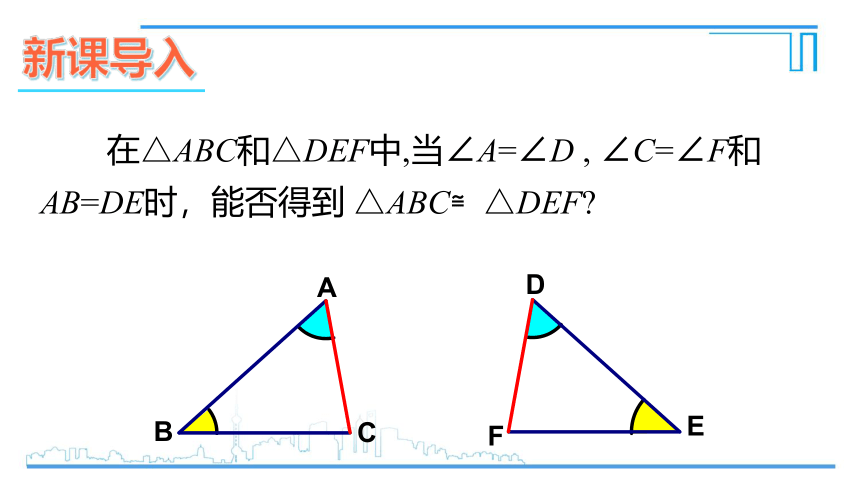
在△ABC和△DEF中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DEF?
根据三角形内角和定理,可知在△ABC和△DEF中,∠B和∠E也相等,这样,在△ABC和△DEF中,可以用ASA来判定△ABC和△DEF全等.
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
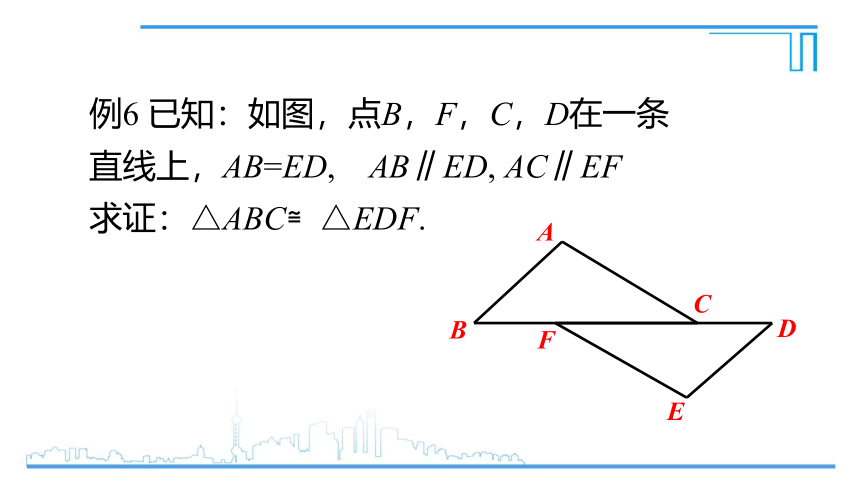
例6 已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED, AC∥EF
求证:△ABC≌△EDF.
E
D
C
F
B
A
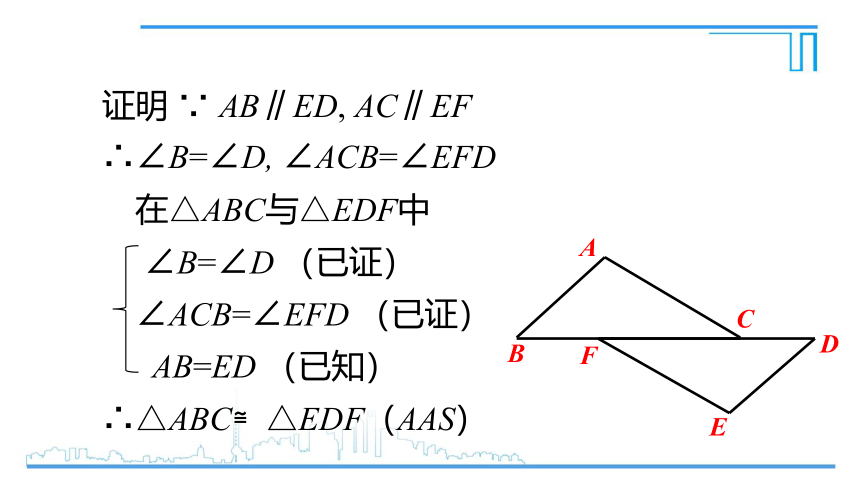
证明 ∵ AB∥ED, AC∥EF
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
E
D
C
F
B
A
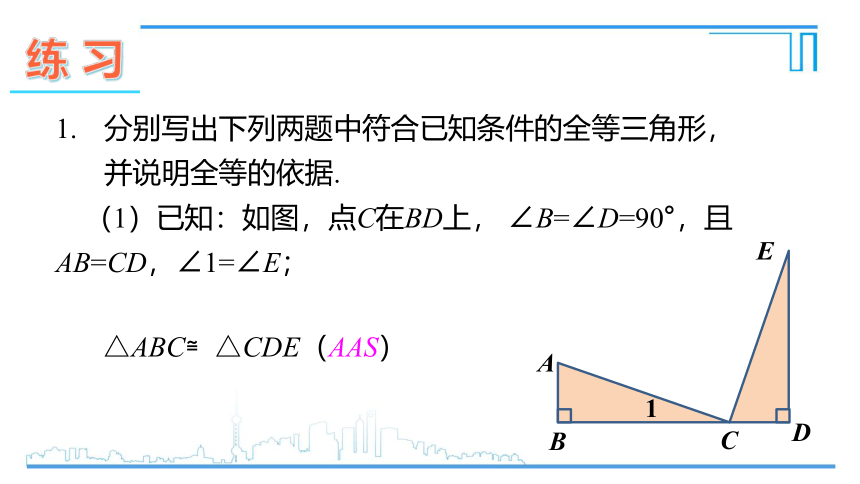
分别写出下列两题中符合已知条件的全等三角形,并说明全等的依据.
(1)已知:如图,点C在BD上, ∠B=∠D=90°,且AB=CD,∠1=∠E;
A
B
C
D
E
1
△ABC≌△CDE(AAS)
(2)已知:如图,AB=DB,BC=BE,∠ABC=∠DBE.
A
B
D
C
E
△ABC≌△DBE(SAS)
2. 如果要使△ABC和△DEF全等,在下列各种情况下还要添加哪些条件?
(1)AB=DE,∠B=∠E;
(2)∠A=∠D,∠C=∠F.
1. 如图:已知AD = AE ,∠B=∠C,
△ABD与△ACE全等吗?为什么?
A
D
E
C
B
⌒
⌒
∴△ABD≌△ACE( AAS )
解:全等.
在△ABD和△ACE
∵
∠B=∠C(已知)
∠A=∠A(公共角)
AD=AE(已知)
2. 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
A
B
C
D
E
1
2
解: △ABC和△ADE全等.
∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ ABC和△ ADE 中
∠C=∠E(已知)
∠BAC=∠DAE(已证)
AB=AD(已知)
∴ △ABC≌△ADE
A
B
C
D
E
1
2
两角分别相等且其中一组等角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
1.从教材习题中选取,
2.完成练习册本课时的习题.
沪科版·八年级上册
在△ABC和△DEF中,当∠A=∠D , ∠C=∠F和AB=DE时,能否得到 △ABC≌△DEF?
根据三角形内角和定理,可知在△ABC和△DEF中,∠B和∠E也相等,这样,在△ABC和△DEF中,可以用ASA来判定△ABC和△DEF全等.
定理 两角分别相等且其中一组等角的对边相等的两个三角形全等(简写成“角角边”或“AAS”).
例6 已知:如图,点B,F,C,D在一条直线上,AB=ED, AB∥ED, AC∥EF
求证:△ABC≌△EDF.
E
D
C
F
B
A
证明 ∵ AB∥ED, AC∥EF
∴∠B=∠D, ∠ACB=∠EFD
在△ABC与△EDF中
∠B=∠D (已证)
∠ACB=∠EFD (已证)
AB=ED (已知)
∴△ABC≌△EDF(AAS)
E
D
C
F
B
A
分别写出下列两题中符合已知条件的全等三角形,并说明全等的依据.
(1)已知:如图,点C在BD上, ∠B=∠D=90°,且AB=CD,∠1=∠E;
A
B
C
D
E
1
△ABC≌△CDE(AAS)
(2)已知:如图,AB=DB,BC=BE,∠ABC=∠DBE.
A
B
D
C
E
△ABC≌△DBE(SAS)
2. 如果要使△ABC和△DEF全等,在下列各种情况下还要添加哪些条件?
(1)AB=DE,∠B=∠E;
(2)∠A=∠D,∠C=∠F.
1. 如图:已知AD = AE ,∠B=∠C,
△ABD与△ACE全等吗?为什么?
A
D
E
C
B
⌒
⌒
∴△ABD≌△ACE( AAS )
解:全等.
在△ABD和△ACE
∵
∠B=∠C(已知)
∠A=∠A(公共角)
AD=AE(已知)
2. 如图,已知∠C=∠E,∠1=∠2,AB=AD,△ABC和△ADE全等吗?为什么?
A
B
C
D
E
1
2
解: △ABC和△ADE全等.
∵∠1=∠2(已知) ∴∠1+∠DAC=∠2+∠DAC
即∠BAC=∠DAE
在△ ABC和△ ADE 中
∠C=∠E(已知)
∠BAC=∠DAE(已证)
AB=AD(已知)
∴ △ABC≌△ADE
A
B
C
D
E
1
2
两角分别相等且其中一组等角的对边相等的两个三角形全等.简写成“角角边”或“AAS”.
1.从教材习题中选取,
2.完成练习册本课时的习题.
