2.2 数轴 课件(共25张PPT)
图片预览






文档简介
第二章 有理数及其运算
2 数轴
知识点一 数轴
画一条水平直线,在直线上取一点表示0(叫做原点);选取某一长度作为单位长度:规定直线向右的为正方向,就得到下面的数轴.
知识点一 数轴
画一条水平直线,在直线上取一点表示0(叫做原点);选取某一长度作为单位长度:规定直线向右的为正方向,就得到下面的数轴.
知识点睛 数轴是一条特殊的直线,它必须同时具备三个要素:①原点:即数轴上表示0的点,它是数轴的“基准点”;②正方向:数轴的正方向具有规定性,习惯上规定从原点向右(或向上)为正方向,从原点向左(或向下)为负方向;③单位长度:单位长度可选取为1cm,0.5cm等,同一数轴上的单位长度必须统一.
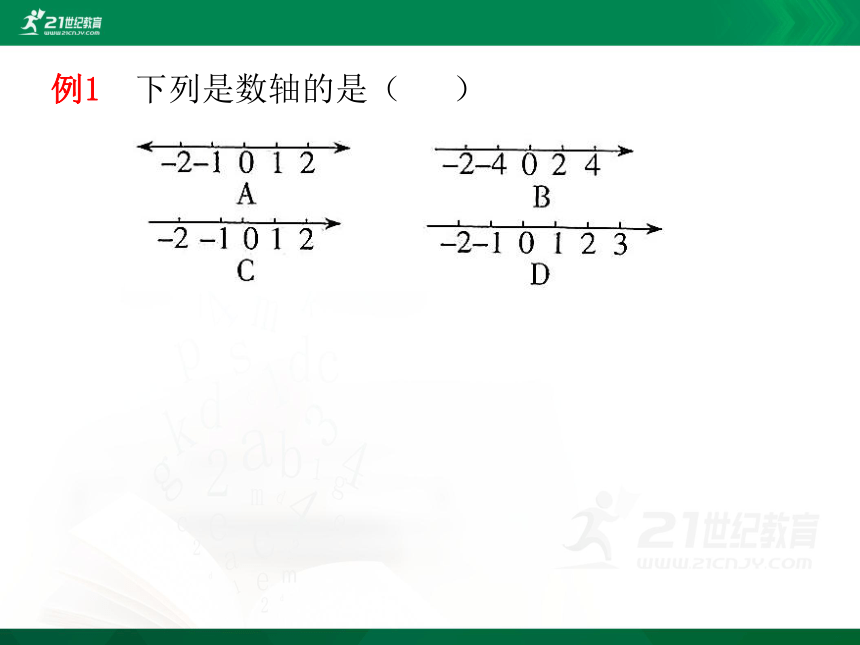
例1 下列是数轴的是( )
例1 下列是数轴的是( )
解析 根据数轴的定义判断,A中负方向画了箭头;B中的数标得不对,-4应与-2交换位置;C中单位长度不统一,故选D.
例1 下列是数轴的是( D )
解析 根据数轴的定义判断,A中负方向画了箭头;B中的数标得不对,-4应与-2交换位置;C中单位长度不统一,故选D.
例1 下列是数轴的是( D )
解析 根据数轴的定义判断,A中负方向画了箭头;B中的数标得不对,-4应与-2交换位置;C中单位长度不统一,故选D.
方法归纳 判断一条直线是不是数轴,一方面需要看这条直线是否满足数轴的三要素:原点、正方向、单位长三者缺一不可;另一方面要看单位长度是否均匀,其大小可以根据不同的需要进行选择.
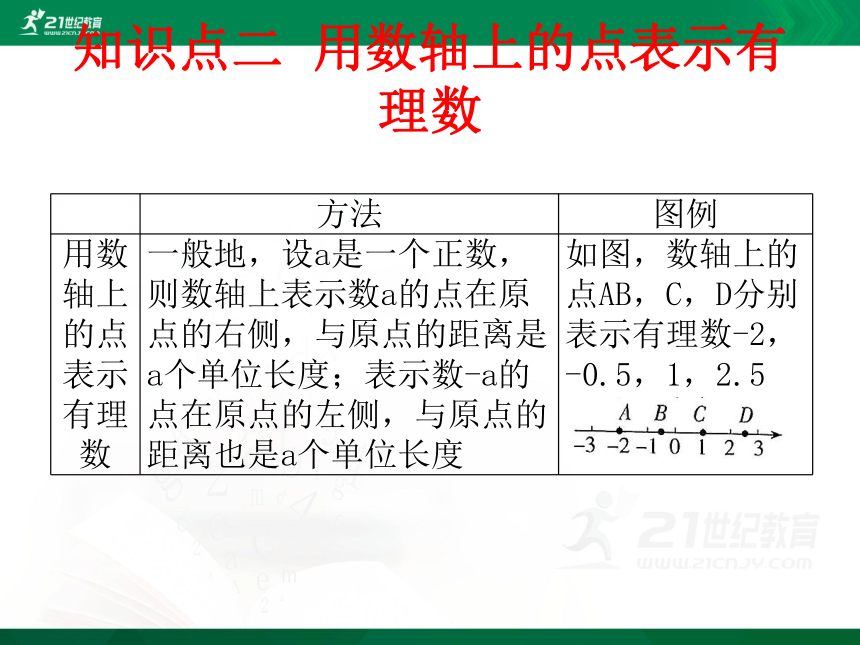
知识点二 用数轴上的点表示有理数
方法
图例
用数轴上的点表示有理数
一般地,设a是一个正数,则数轴上表示数a的点在原点的右侧,与原点的距离是a个单位长度;表示数-a的点在原点的左侧,与原点的距离也是a个单位长度
如图,数轴上的点AB,C,D分别表示有理数-2,-0.5,1,2.5
知识解读
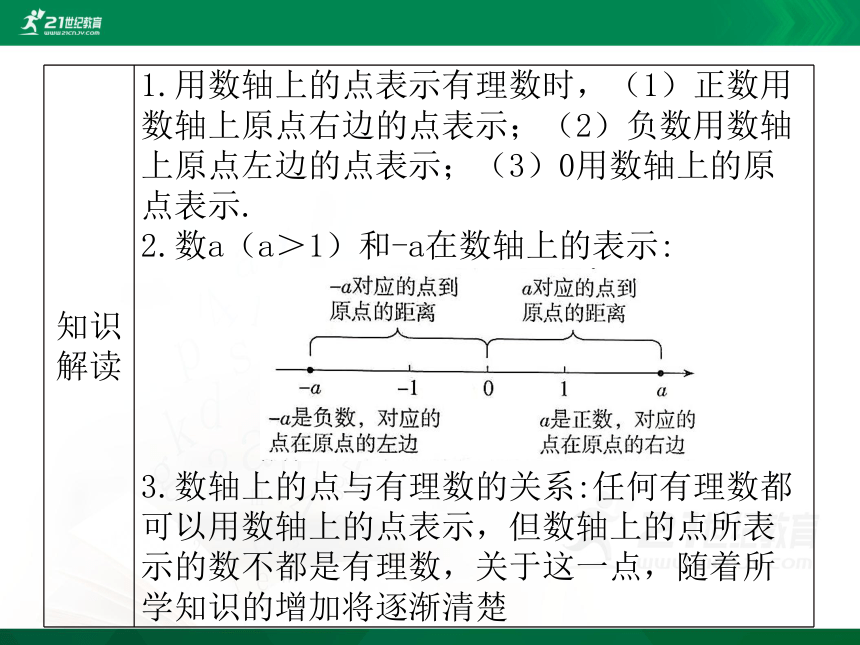
1.用数轴上的点表示有理数时,(1)正数用数轴上原点右边的点表示;(2)负数用数轴上原点左边的点表示;(3)0用数轴上的原点表示.
2.数a(a>1)和-a在数轴上的表示:
3.数轴上的点与有理数的关系:任何有理数都可以用数轴上的点表示,但数轴上的点所表示的数不都是有理数,关于这一点,随着所学知识的增加将逐渐清楚
知识点三 利用数轴比较有理数的大小
利用数轴比较
有理数的大小
数轴上两个点表示的数,右边的总比左边的大
正数大于0,负数小于0正数大于负数
特别提示
(1)正数大于0,且大于0的数都是正数,因此可以用“a>0”表示a为正数;负数小于0,且小于0的数都是负数,因此可以用“a<0”表示a为负数;a≥0表示a为非负数,a≤0表示a为非正数;
(2)利用数轴比较有理数的大小适用于“两个正数”(或“两个负数”)比较大小及“一个正数与一个负数”比较大小,“一个正数与一个负数”也可根据“正数大于一切负数”比较大小.
经典例题
题型一 利用数轴解决实际问题
例1 邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村多远?
(2)邮递员一共骑行了多少千米?
题型一 利用数轴解决实际问题
例1 邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村多远?
(2)邮递员一共骑行了多少千米?
解析 (1)如图所示,C村离A村5km远.
(2)3+2+7+3+5=20km.
答:邮递员一共骑行了20千米.
题型一 利用数轴解决实际问题
例1 邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村多远?
(2)邮递员一共骑行了多少千米?
解析 (1)如图所示,C村离A村5km远.
(2)3+2+7+3+5=20km.
答:邮递员一共骑行了20千米.
特别提示 根据题目信息,理解数量关系并画出数轴是解题的关键.
题型二 利用数轴解决动点问题
例2 按照要求在数轴上完成点的移动,并说明移动后点表示的数是什么.
(1)点A在数轴上表示的数是-2,将A向右移动5个单位,那么点A表示的新数是什么?
(2)点B在数轴上表示的数是3,将B向右移动5个单位,再向左移动2个单位,那么点B表示的新数是什么?
(3)点C在数轴上,将它向右移动4个单位后,再向左移动1个单位正好到原点,那么点C原来表示的数是什么?
解析 (1)点A在数轴上表示的数是-2,将A向右移动5个单位后的位置如图所示.
所以点A表示的新数是3.
(2)点B在数轴上表示的数是3,将B向右移动5个单位,再向左移动2个单位后的位置如图所示.
所以点B表示的新数是6.
(3)逆推点C的移动过程,点C在原点处先向右移动1个单位,再向左移动4个单位后的位置如图所示.
所以点C原来表示的数为-3.
(3)逆推点C的移动过程,点C在原点处先向右移动1个单位,再向左移动4个单位后的位置如图所示.
所以点C原来表示的数为-3.
点拨 对于数轴上点的位置移动问题一定要注意移动的方向和距离.
2 数轴
知识点一 数轴
画一条水平直线,在直线上取一点表示0(叫做原点);选取某一长度作为单位长度:规定直线向右的为正方向,就得到下面的数轴.
知识点一 数轴
画一条水平直线,在直线上取一点表示0(叫做原点);选取某一长度作为单位长度:规定直线向右的为正方向,就得到下面的数轴.
知识点睛 数轴是一条特殊的直线,它必须同时具备三个要素:①原点:即数轴上表示0的点,它是数轴的“基准点”;②正方向:数轴的正方向具有规定性,习惯上规定从原点向右(或向上)为正方向,从原点向左(或向下)为负方向;③单位长度:单位长度可选取为1cm,0.5cm等,同一数轴上的单位长度必须统一.
例1 下列是数轴的是( )
例1 下列是数轴的是( )
解析 根据数轴的定义判断,A中负方向画了箭头;B中的数标得不对,-4应与-2交换位置;C中单位长度不统一,故选D.
例1 下列是数轴的是( D )
解析 根据数轴的定义判断,A中负方向画了箭头;B中的数标得不对,-4应与-2交换位置;C中单位长度不统一,故选D.
例1 下列是数轴的是( D )
解析 根据数轴的定义判断,A中负方向画了箭头;B中的数标得不对,-4应与-2交换位置;C中单位长度不统一,故选D.
方法归纳 判断一条直线是不是数轴,一方面需要看这条直线是否满足数轴的三要素:原点、正方向、单位长三者缺一不可;另一方面要看单位长度是否均匀,其大小可以根据不同的需要进行选择.
知识点二 用数轴上的点表示有理数
方法
图例
用数轴上的点表示有理数
一般地,设a是一个正数,则数轴上表示数a的点在原点的右侧,与原点的距离是a个单位长度;表示数-a的点在原点的左侧,与原点的距离也是a个单位长度
如图,数轴上的点AB,C,D分别表示有理数-2,-0.5,1,2.5
知识解读
1.用数轴上的点表示有理数时,(1)正数用数轴上原点右边的点表示;(2)负数用数轴上原点左边的点表示;(3)0用数轴上的原点表示.
2.数a(a>1)和-a在数轴上的表示:
3.数轴上的点与有理数的关系:任何有理数都可以用数轴上的点表示,但数轴上的点所表示的数不都是有理数,关于这一点,随着所学知识的增加将逐渐清楚
知识点三 利用数轴比较有理数的大小
利用数轴比较
有理数的大小
数轴上两个点表示的数,右边的总比左边的大
正数大于0,负数小于0正数大于负数
特别提示
(1)正数大于0,且大于0的数都是正数,因此可以用“a>0”表示a为正数;负数小于0,且小于0的数都是负数,因此可以用“a<0”表示a为负数;a≥0表示a为非负数,a≤0表示a为非正数;
(2)利用数轴比较有理数的大小适用于“两个正数”(或“两个负数”)比较大小及“一个正数与一个负数”比较大小,“一个正数与一个负数”也可根据“正数大于一切负数”比较大小.
经典例题
题型一 利用数轴解决实际问题
例1 邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村多远?
(2)邮递员一共骑行了多少千米?
题型一 利用数轴解决实际问题
例1 邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村多远?
(2)邮递员一共骑行了多少千米?
解析 (1)如图所示,C村离A村5km远.
(2)3+2+7+3+5=20km.
答:邮递员一共骑行了20千米.
题型一 利用数轴解决实际问题
例1 邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村多远?
(2)邮递员一共骑行了多少千米?
解析 (1)如图所示,C村离A村5km远.
(2)3+2+7+3+5=20km.
答:邮递员一共骑行了20千米.
特别提示 根据题目信息,理解数量关系并画出数轴是解题的关键.
题型二 利用数轴解决动点问题
例2 按照要求在数轴上完成点的移动,并说明移动后点表示的数是什么.
(1)点A在数轴上表示的数是-2,将A向右移动5个单位,那么点A表示的新数是什么?
(2)点B在数轴上表示的数是3,将B向右移动5个单位,再向左移动2个单位,那么点B表示的新数是什么?
(3)点C在数轴上,将它向右移动4个单位后,再向左移动1个单位正好到原点,那么点C原来表示的数是什么?
解析 (1)点A在数轴上表示的数是-2,将A向右移动5个单位后的位置如图所示.
所以点A表示的新数是3.
(2)点B在数轴上表示的数是3,将B向右移动5个单位,再向左移动2个单位后的位置如图所示.
所以点B表示的新数是6.
(3)逆推点C的移动过程,点C在原点处先向右移动1个单位,再向左移动4个单位后的位置如图所示.
所以点C原来表示的数为-3.
(3)逆推点C的移动过程,点C在原点处先向右移动1个单位,再向左移动4个单位后的位置如图所示.
所以点C原来表示的数为-3.
点拨 对于数轴上点的位置移动问题一定要注意移动的方向和距离.
