11.1.1空间几何体与斜二测画法 教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.1空间几何体与斜二测画法 教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册 |

|
|
| 格式 | docx | ||
| 文件大小 | 278.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 12:29:22 | ||
图片预览



文档简介
11.1.1空间几何体与斜二测画法
教案
教学课时:1课时
教学目标:
1、利用实物、计算机软件等观察空间图形,认识柱、锥、台、球及简单组合体的结构特征,能运用这些特征描述现实生活中简单物体的结构;
2、能用斜二测画法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合);
3、运用直观感知和动手操作建立空间观念,培养数学抽象与直观想象的核心素养.
教学重点:
斜二测画法.
教学难点:
斜二测画法画空间立体图形的直观图.
教学过程:
一、空间几何体
问题一:观察下列图片所示的建筑物,将每个建筑物可抽象出的几何体画出来.
【学生活动】
观察图片,绘制棱锥、球、圆锥、棱台的直观图.
【设计意图】
本节课是立体几何的第一课,需要给学生更为直观的体验,所以这里先利用实物观察空间图形,让他们复习在小与初中阶段学习过的柱、锥、台、球及简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.通过实物抽象出几何体,这是一个数学抽象和空间想象的过程,着重培养这两方面的核心素养,为接下来的学习做好准备.
二、斜二测画法
1、水平放置的平面图形的直观图
问题二:一个水平放置的长方形,怎么画更有立体感?
【学生活动】
学生从不同角度观察长方形模型,绘制直观图.
分析:水平放置的长方形看起来并不像是长方形,而更像是平行四边形,所以这里我们使用斜二测画法来作直观图.
立体几何中,用来表示空间图形的平面图形,称为空间图形的直观图.
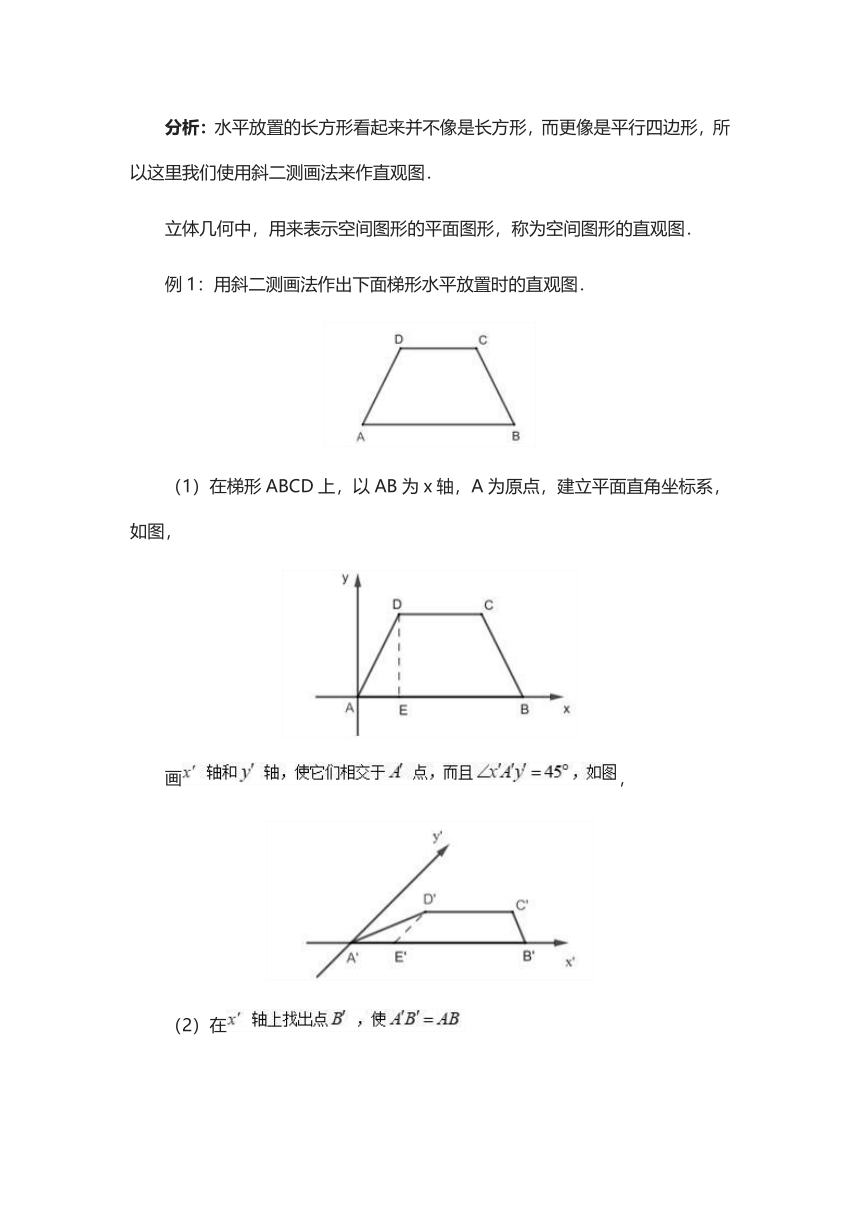
例1:用斜二测画法作出下面梯形水平放置时的直观图.
(1)在梯形ABCD上,以AB为x轴,A为原点,建立平面直角坐标系,如图,
画,
(2)在
过D点作AB的垂线,设垂足为E,连接DE.在图,使.
作.
过.
(3)连就是梯形ABCD的直观图.
【设计意图】
在学生完成探究之后,采用传统的讲授法给学生讲解斜二测画法,给学生建立起规范化的作图意识,也让学生体会到严谨的数学之美.
小结:用斜二测画法作水平放置的平面图形直观图的步骤.
(1)在平面图形上取互相垂直的x轴和y轴,作出与之对应的轴和轴,使得它们正方向的夹角为.
(2)平面图形中与x轴平行(或重合)的线段画成与轴重合(或平行)的线段,且长度不变.平面图形中与y轴平行(或重合)的线段画成与轴重合(或平行)的线段,且长度为原来长度的一半.
(3)连接有关线段,擦去作图过程中的辅助线.
2、立体图形的直观图
问题三:怎么画出一个长方体的直观图?
【学生活动】
学生通过观察实物模型,分组研究作图方法并进行同伴互评.
分析:长方体的水平面可以按照上面的画法先绘制出来,接下来的重点是竖直方向的图形应该怎么表示,通过观察,竖直方向的图形从正面观察形状并不会发生变化,所以可以通过建立竖直坐标轴轴并保持平行与该轴的线段等长即可.
(1)首先,用上面的方法作出水平放置的长为4宽为3的长方形的直观图ABCD(保留坐标轴).
(2)过A作轴,使之垂直于轴.在轴上截取.过B,C,D分别作的平行线并使,然后连接,.
(3)擦去作图过程中的辅助线,并把被面遮挡住的线段AD,DC,改成虚线(或擦除).由此得到的就是所求长方体的直观图.
小结:用斜二测画法作立体图形直观图的步骤.
(1)在立体图形中取水平平面,在其中取互相垂直的X轴与Y轴,作出水平平面上图形的直观图(保留轴轴).
(2)在立体图形中,过x轴与y轴的交点取z轴,并使z轴垂直于x轴与y轴.过轴与轴的交点作z轴对应的轴,且轴垂直于轴.图形中与z轴平行(或重合)的线段画成与轴平行(或重合)的线段,且长度不变.连接有关线段.
(3)擦去辅助线,并把被面遮挡住的线段改成虚线(或擦除).
口诀:平行依旧垂改斜,横等纵半竖不变;眼见为实遮为虚,空间观感好体现.
【设计意图】
从平面到空间,从二维到三维进行过渡,这里是本节课的难点,让学生从最简单的长方体开始学习,给出斜二测画法画空间图形的基本步骤,这也符合学生的认知规律,掌握规则之后学生就可以将之迁移到其它的多面体当中去.
3、图柱与球的直观图
水平放置的圆,不是采用斜二测画法,而是采用“正等测画法”画成椭圆,如图所示是球与圆柱的直观图的画法.
三、用信息技术观察几何体
例2:利用GeoGebra软件的“3D绘图”,作出长方体,进行放大、缩小、旋转操作,从不同的角度观察几何体.
【学生活动】
用GeoGebra软件作出常见的空间几何体,并旋转视图,从不同的角度观察.
【设计意图】
以往课堂中更多的是使用实物模型来增强学生的立体感,随着信息技术的发展,现在可以更多的借助信息技术研究空间几何体的结构,使用数学软件创设3D情境,让学生可以多角度观察大量不同的几何体,培养直观想象的核心素养.此外,用电脑屏幕展示立体图形,本质上呈现的是立体图形的直观图,也就是用二维图形可表示三维图形,更有利于学生掌握直观图的画法.
四、课后作业:
P59练习A,习题2、3、6,练习B,习题2、4.
教案
教学课时:1课时
教学目标:
1、利用实物、计算机软件等观察空间图形,认识柱、锥、台、球及简单组合体的结构特征,能运用这些特征描述现实生活中简单物体的结构;
2、能用斜二测画法画出简单空间图形(长方体、球、圆柱、圆锥、棱柱及其简单组合);
3、运用直观感知和动手操作建立空间观念,培养数学抽象与直观想象的核心素养.
教学重点:
斜二测画法.
教学难点:
斜二测画法画空间立体图形的直观图.
教学过程:
一、空间几何体
问题一:观察下列图片所示的建筑物,将每个建筑物可抽象出的几何体画出来.
【学生活动】
观察图片,绘制棱锥、球、圆锥、棱台的直观图.
【设计意图】
本节课是立体几何的第一课,需要给学生更为直观的体验,所以这里先利用实物观察空间图形,让他们复习在小与初中阶段学习过的柱、锥、台、球及简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.通过实物抽象出几何体,这是一个数学抽象和空间想象的过程,着重培养这两方面的核心素养,为接下来的学习做好准备.
二、斜二测画法
1、水平放置的平面图形的直观图
问题二:一个水平放置的长方形,怎么画更有立体感?
【学生活动】
学生从不同角度观察长方形模型,绘制直观图.
分析:水平放置的长方形看起来并不像是长方形,而更像是平行四边形,所以这里我们使用斜二测画法来作直观图.
立体几何中,用来表示空间图形的平面图形,称为空间图形的直观图.
例1:用斜二测画法作出下面梯形水平放置时的直观图.
(1)在梯形ABCD上,以AB为x轴,A为原点,建立平面直角坐标系,如图,
画,
(2)在
过D点作AB的垂线,设垂足为E,连接DE.在图,使.
作.
过.
(3)连就是梯形ABCD的直观图.
【设计意图】
在学生完成探究之后,采用传统的讲授法给学生讲解斜二测画法,给学生建立起规范化的作图意识,也让学生体会到严谨的数学之美.
小结:用斜二测画法作水平放置的平面图形直观图的步骤.
(1)在平面图形上取互相垂直的x轴和y轴,作出与之对应的轴和轴,使得它们正方向的夹角为.
(2)平面图形中与x轴平行(或重合)的线段画成与轴重合(或平行)的线段,且长度不变.平面图形中与y轴平行(或重合)的线段画成与轴重合(或平行)的线段,且长度为原来长度的一半.
(3)连接有关线段,擦去作图过程中的辅助线.
2、立体图形的直观图
问题三:怎么画出一个长方体的直观图?
【学生活动】
学生通过观察实物模型,分组研究作图方法并进行同伴互评.
分析:长方体的水平面可以按照上面的画法先绘制出来,接下来的重点是竖直方向的图形应该怎么表示,通过观察,竖直方向的图形从正面观察形状并不会发生变化,所以可以通过建立竖直坐标轴轴并保持平行与该轴的线段等长即可.
(1)首先,用上面的方法作出水平放置的长为4宽为3的长方形的直观图ABCD(保留坐标轴).
(2)过A作轴,使之垂直于轴.在轴上截取.过B,C,D分别作的平行线并使,然后连接,.
(3)擦去作图过程中的辅助线,并把被面遮挡住的线段AD,DC,改成虚线(或擦除).由此得到的就是所求长方体的直观图.
小结:用斜二测画法作立体图形直观图的步骤.
(1)在立体图形中取水平平面,在其中取互相垂直的X轴与Y轴,作出水平平面上图形的直观图(保留轴轴).
(2)在立体图形中,过x轴与y轴的交点取z轴,并使z轴垂直于x轴与y轴.过轴与轴的交点作z轴对应的轴,且轴垂直于轴.图形中与z轴平行(或重合)的线段画成与轴平行(或重合)的线段,且长度不变.连接有关线段.
(3)擦去辅助线,并把被面遮挡住的线段改成虚线(或擦除).
口诀:平行依旧垂改斜,横等纵半竖不变;眼见为实遮为虚,空间观感好体现.
【设计意图】
从平面到空间,从二维到三维进行过渡,这里是本节课的难点,让学生从最简单的长方体开始学习,给出斜二测画法画空间图形的基本步骤,这也符合学生的认知规律,掌握规则之后学生就可以将之迁移到其它的多面体当中去.
3、图柱与球的直观图
水平放置的圆,不是采用斜二测画法,而是采用“正等测画法”画成椭圆,如图所示是球与圆柱的直观图的画法.
三、用信息技术观察几何体
例2:利用GeoGebra软件的“3D绘图”,作出长方体,进行放大、缩小、旋转操作,从不同的角度观察几何体.
【学生活动】
用GeoGebra软件作出常见的空间几何体,并旋转视图,从不同的角度观察.
【设计意图】
以往课堂中更多的是使用实物模型来增强学生的立体感,随着信息技术的发展,现在可以更多的借助信息技术研究空间几何体的结构,使用数学软件创设3D情境,让学生可以多角度观察大量不同的几何体,培养直观想象的核心素养.此外,用电脑屏幕展示立体图形,本质上呈现的是立体图形的直观图,也就是用二维图形可表示三维图形,更有利于学生掌握直观图的画法.
四、课后作业:
P59练习A,习题2、3、6,练习B,习题2、4.
