11.1.2构成空间几何体的基本元素(第1课时)教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.2构成空间几何体的基本元素(第1课时)教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册 |

|
|
| 格式 | docx | ||
| 文件大小 | 322.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 12:30:10 | ||
图片预览

文档简介
11.1.2构成空间几何体的基本元素第一课时教案
教学课时:第1课时
教学目标:
1、
结合学生已经学习掌握的相关知识,并通过实物与多媒体动态演示使学生初步认识空间中的点、线、面这些基本元素,并掌握点与直线、直线与直线的位置关系;
2、
学会用符合表示点、直线及点与直线的关系;
3、
通过实例及动态演示进一步培养学生的空间想象能力.
教学重点:
从运动的观点来初步认识空间中的点、线、面、体之间的生成关系,点与直线、直线与直线,直线在平面内、直线与平面相交,平面与平面相交等位置关系.
教学难点:
通过几何体的直观图观察基本元素之间的关系,点与直线、直线与直线、直线与平面、平面与平面的关系及表示,尤其是对两条直线异面定义的理解.
教学过程:
一、点与直线、直线与直线的位置关系及表示
提出问题,解决问题:
问题1:接触过哪些几何体?这些几何体由什么构成的?
问题2:这些元素之间有什么关系?
点运动成线,线运动成面,面运动成体.
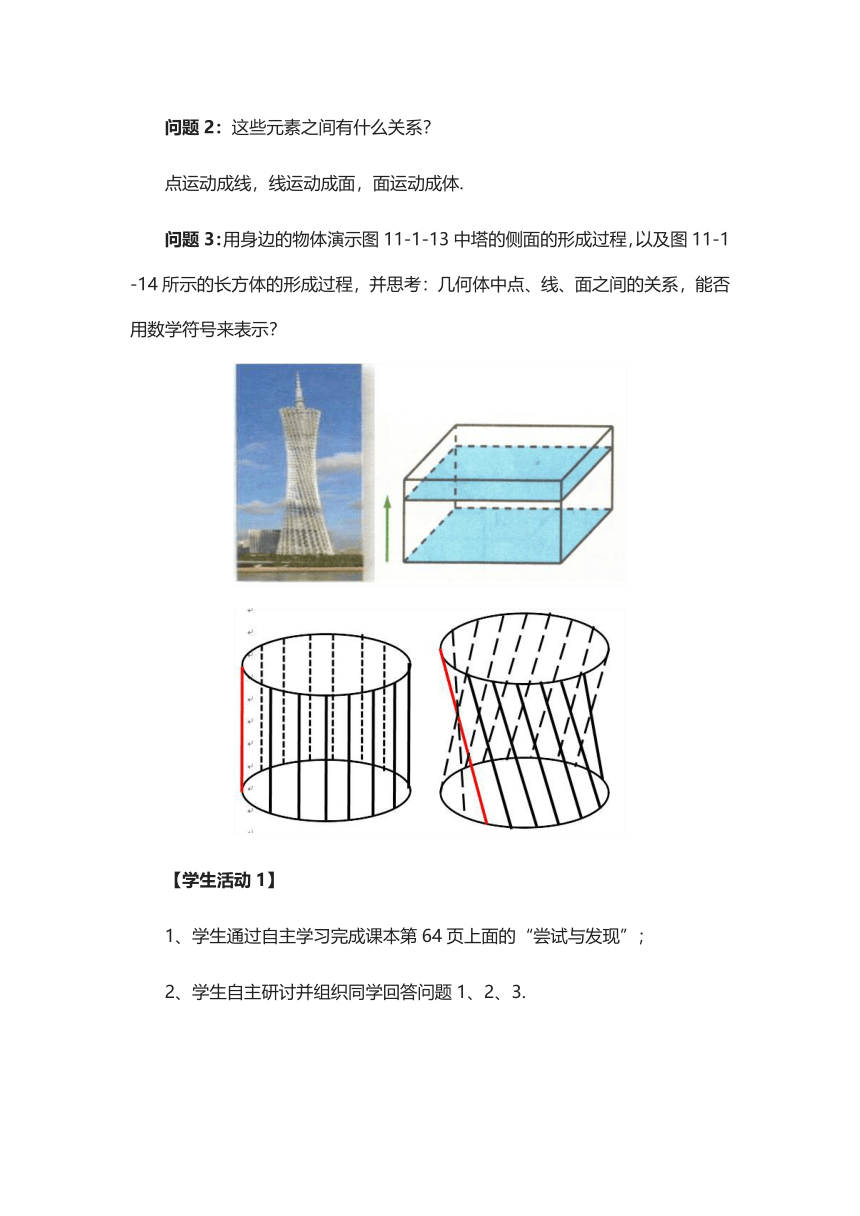
问题3:用身边的物体演示图11-1-13中塔的侧面的形成过程,以及图11-1
-14所示的长方体的形成过程,并思考:几何体中点、线、面之间的关系,能否用数学符号来表示?
【学生活动1】
1、学生通过自主学习完成课本第64页上面的“尝试与发现”;
2、学生自主研讨并组织同学回答问题1、2、3.
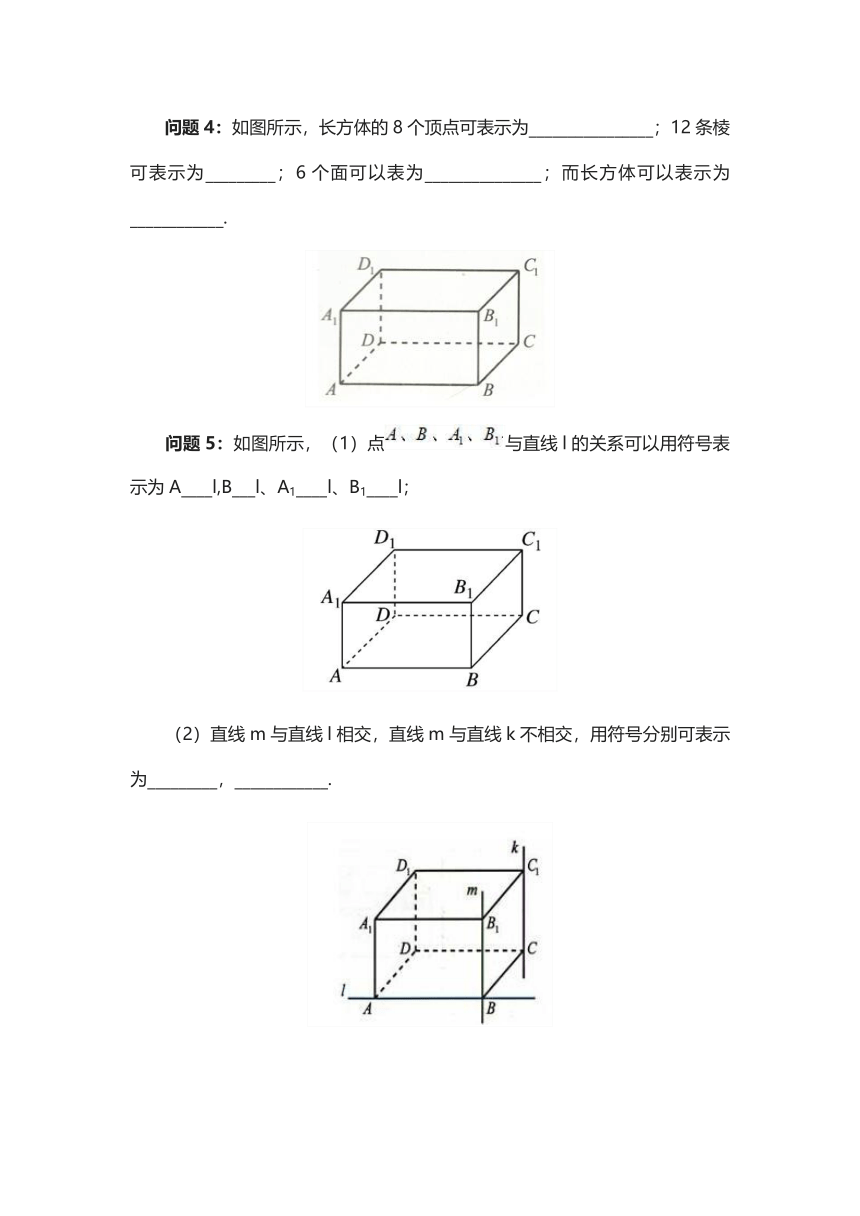
问题4:如图所示,长方体的8个顶点可表示为________________;12条棱可表示为_________;6个面可以表为_______________;而长方体可以表示为____________.
问题5:如图所示,(1)点与直线l的关系可以用符号表示为A____l,B___l、A1____l、B1____l;
(2)直线m与直线l相交,直线m与直线k不相交,用符号分别可表示为_________,____________.
【学生活动2】
1、学生通过自主学习、分组讨论完成课本62页“尝试与发现”;
2、总结空间点与直线、直线与直线的位置关系.
两条直线的位置关系:平行、相交、异面.
【设计意图】
由于学生空间几何体有一些基本的认识,通过自主学习可以完成以上大部分问题,教师只需在关键的位置给学生必要的指导即可,当然对于点与直线、直线与直线位置关系的符号表示要重点强调.
课堂练习:
1、P65练
A3、4;
2.在长方体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
A.3
B.4
C.5
D.6
答案:C
解析:如图,用列举法知符合要求的棱为BC,CD,.
1、如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的为____________.
答案:3
解析:还原后的正方体如图,
其中AB与CD、AB与GH、EF与GH为异面直线,共3对.
【设计意图】
及时的练习可以强化学生对以学知识的认识.
二、直线与平面、平面与平面的基本关系及表示
【师生互动】
教师用教具演示:观察下列每个图形中,直线的位置关系.
师生共同研究总结点与平面、直线与平面的关系.
1、平面的符号表示:长方形ABCD所在的平面可记作面ABC,也可记作面ABD或面ABCD;平面的习惯表示是用小写希腊字母···表示.
2、A是平面内的点,不是平面内的点,用符号简写为_______________.
3、直线l在平面内(或平面过直线l),记作__________;直线m与平面有且只有一个公共点B(称为直线m与平面相交),用符号简写为__________;直线上至少有一个点不在平面内,称为直线在平面外,若直线为m,记作________.
4、长方形所在的平面为,如图所示与有公共点,称为平面与平面相交,记作____________.
【设计意图】
教师演示、学生观察,多角度展示直线与平面的位置关系,强化感性认识;学生自主阅读,观察课本图11-1-17,提高学生的抽象识图能力,动静结合,进一步培养学生的空间想象能力.
三、课堂练习
P65练
B1、P66
练
B3、6.
【设计意图】
及时的练习可以强化学生对以学知识的认识.
四、归纳总结
1、点与直线、平面的位置关系,直线与直线的位置关系,直线在平面内与直线与平面相交,平面与平面相交.
2、位置关系的符号表示.
五:作业
联系生活中的实际,画出所见到的实物的平面直观图,体现出直线与直线,直线与平面间的关系.
教学课时:第1课时
教学目标:
1、
结合学生已经学习掌握的相关知识,并通过实物与多媒体动态演示使学生初步认识空间中的点、线、面这些基本元素,并掌握点与直线、直线与直线的位置关系;
2、
学会用符合表示点、直线及点与直线的关系;
3、
通过实例及动态演示进一步培养学生的空间想象能力.
教学重点:
从运动的观点来初步认识空间中的点、线、面、体之间的生成关系,点与直线、直线与直线,直线在平面内、直线与平面相交,平面与平面相交等位置关系.
教学难点:
通过几何体的直观图观察基本元素之间的关系,点与直线、直线与直线、直线与平面、平面与平面的关系及表示,尤其是对两条直线异面定义的理解.
教学过程:
一、点与直线、直线与直线的位置关系及表示
提出问题,解决问题:
问题1:接触过哪些几何体?这些几何体由什么构成的?
问题2:这些元素之间有什么关系?
点运动成线,线运动成面,面运动成体.
问题3:用身边的物体演示图11-1-13中塔的侧面的形成过程,以及图11-1
-14所示的长方体的形成过程,并思考:几何体中点、线、面之间的关系,能否用数学符号来表示?
【学生活动1】
1、学生通过自主学习完成课本第64页上面的“尝试与发现”;
2、学生自主研讨并组织同学回答问题1、2、3.
问题4:如图所示,长方体的8个顶点可表示为________________;12条棱可表示为_________;6个面可以表为_______________;而长方体可以表示为____________.
问题5:如图所示,(1)点与直线l的关系可以用符号表示为A____l,B___l、A1____l、B1____l;
(2)直线m与直线l相交,直线m与直线k不相交,用符号分别可表示为_________,____________.
【学生活动2】
1、学生通过自主学习、分组讨论完成课本62页“尝试与发现”;
2、总结空间点与直线、直线与直线的位置关系.
两条直线的位置关系:平行、相交、异面.
【设计意图】
由于学生空间几何体有一些基本的认识,通过自主学习可以完成以上大部分问题,教师只需在关键的位置给学生必要的指导即可,当然对于点与直线、直线与直线位置关系的符号表示要重点强调.
课堂练习:
1、P65练
A3、4;
2.在长方体ABCD-A1B1C1D1中,既与AB共面也与CC1共面的棱的条数为( )
A.3
B.4
C.5
D.6
答案:C
解析:如图,用列举法知符合要求的棱为BC,CD,.
1、如图为正方体表面的一种展开图,则图中的四条线段AB,CD,EF,GH在原正方体中互为异面的为____________.
答案:3
解析:还原后的正方体如图,
其中AB与CD、AB与GH、EF与GH为异面直线,共3对.
【设计意图】
及时的练习可以强化学生对以学知识的认识.
二、直线与平面、平面与平面的基本关系及表示
【师生互动】
教师用教具演示:观察下列每个图形中,直线的位置关系.
师生共同研究总结点与平面、直线与平面的关系.
1、平面的符号表示:长方形ABCD所在的平面可记作面ABC,也可记作面ABD或面ABCD;平面的习惯表示是用小写希腊字母···表示.
2、A是平面内的点,不是平面内的点,用符号简写为_______________.
3、直线l在平面内(或平面过直线l),记作__________;直线m与平面有且只有一个公共点B(称为直线m与平面相交),用符号简写为__________;直线上至少有一个点不在平面内,称为直线在平面外,若直线为m,记作________.
4、长方形所在的平面为,如图所示与有公共点,称为平面与平面相交,记作____________.
【设计意图】
教师演示、学生观察,多角度展示直线与平面的位置关系,强化感性认识;学生自主阅读,观察课本图11-1-17,提高学生的抽象识图能力,动静结合,进一步培养学生的空间想象能力.
三、课堂练习
P65练
B1、P66
练
B3、6.
【设计意图】
及时的练习可以强化学生对以学知识的认识.
四、归纳总结
1、点与直线、平面的位置关系,直线与直线的位置关系,直线在平面内与直线与平面相交,平面与平面相交.
2、位置关系的符号表示.
五:作业
联系生活中的实际,画出所见到的实物的平面直观图,体现出直线与直线,直线与平面间的关系.
