11.1.6祖暅原理与几何体的体积(第2课时)教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.1.6祖暅原理与几何体的体积(第2课时)教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册 |

|
|
| 格式 | docx | ||
| 文件大小 | 80.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 00:00:00 | ||
图片预览


文档简介
11.1.6祖暅原理与几何体的体积第二课时教案
教学课时:第2课时
教学目标:
1.、结合学生已经学习掌握的祖暅原理、棱柱棱锥相关知识,推导棱台、球体的体积公式;
2、引导学生解决组合体体积相关问题;
3、提高学生归纳与总结,计算与推理的能力,鼓励学生积极探索体积公式的推导,逐步提高学生数学探究的能力与合作的能力.
教学重点:
棱台和球体积公式的推理过程.
教学难点:
对体积公式的应用和组合体体积问题的解决.
教学过程:
一、提出问题,解决问题:
问题1:上节课我们学过柱体和锥体的体积公式你还记得吗?我们知道,棱台与圆台统称为台体,那么台体的体积可以通过我们已知的知识得到吗?
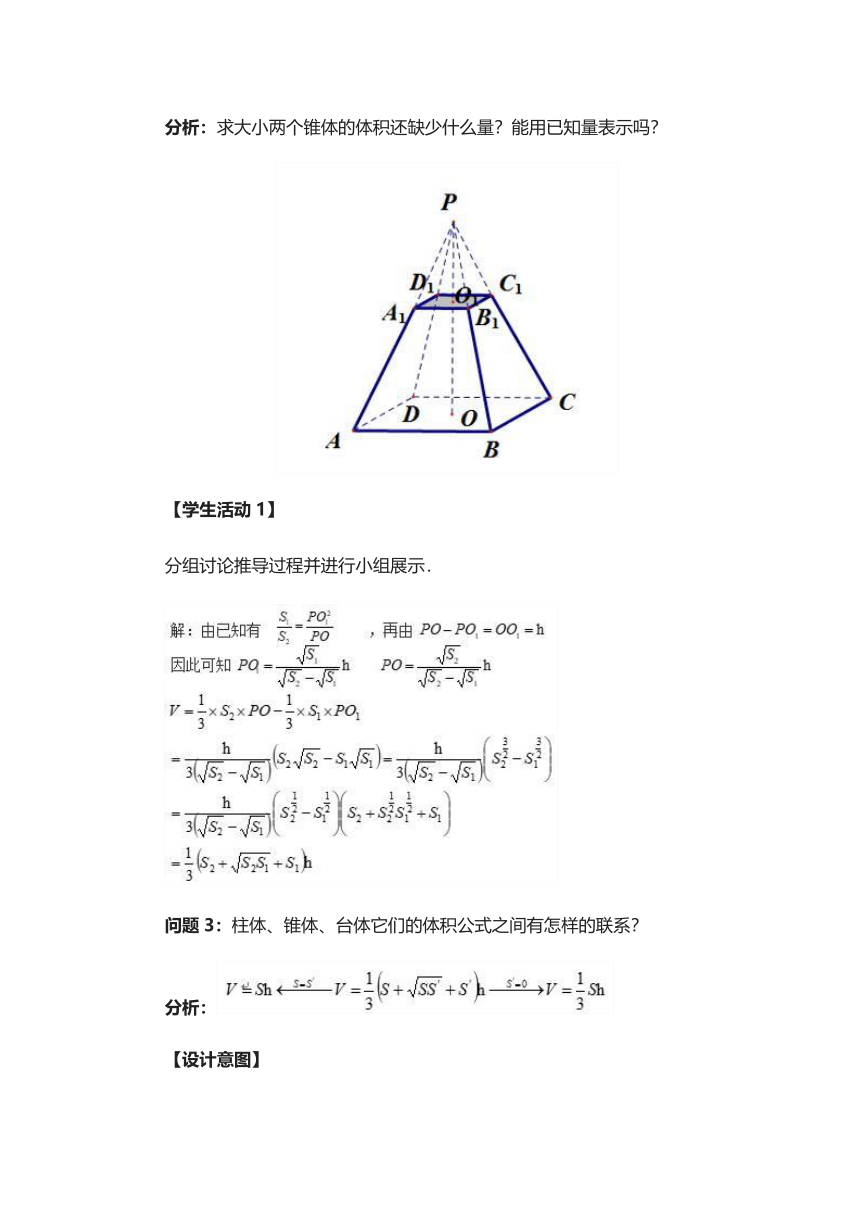
问题2:已知四棱台上、下底面面积分别为,而且高为h,求这个棱台的体积.
分析:求大小两个锥体的体积还缺少什么量?能用已知量表示吗?
【学生活动1】
分组讨论推导过程并进行小组展示.
问题3:柱体、锥体、台体它们的体积公式之间有怎样的联系?
分析:
【设计意图】
通过学生对柱体、锥体和台体体积公式的结构分析,让学生更清楚的认识到三种几何体之间的联系,帮助学生加深对公式的理解.
问题4:(1)你能想出什么办法测出一个兵乓球的体积?
(2)如图所示是底面积和高都相等的两个几何体,左边是半球,右边是圆柱被挖去一个倒立的圆锥剩余的部分,用平行于半球与圆柱底面的平面去截这两个几何体,所得截面分别是什么形状?两个截面面积大小关系怎样?由此你能得到球的体积公式吗?
分析:半球的截面的面积,是两个圆的面积之差,引引导学生找两个同心圆,从而探索到这个几何体为圆柱中挖去一个等底面积等高的圆锥,从而利用祖暅原理得到:半球的体积=底面半径和高为R圆柱的体积—等底同高的圆锥的体积.
【学生活动2】
分组讨论并进行小组展示.
【设计意图】
让学生通过讨论和结果展示,参与到结论的形成过程中来,从而加深对公式的理解.
拓展:在我国球的体积研究由来已久,公元五、六世纪南北朝时期的祖暅在数学家刘徽的基础上,利用“牟合方盖”和“祖暅原理”推导出了球的体积公式,感兴趣的同学可以参考书后的拓展阅读.
二、例题讲解,深化理解
例(课本85页例3)
如图,某铁制零件由一个正四棱柱和一个球组成,已知正四棱柱底面边长与球的直径均为1cm,正四棱柱的高为2cm,现有这种零件一盒共50kg,取铁的密度为.
(1)估计有多少个这样的零件;
(2)如果要给这盒零件的每个零件表面涂上一种特殊的材料,则需要能涂多少平方厘米的材料(球与接口处的面积不计,结果精确到)?
解:(1)每个零件的体积为
因此每个零件的质量为
因此可估计出零件的个数
(2)每个零件的表面积为
因此零件的表面积之和约为
即需要能涂的材料.
【设计意图】鼓励学生尝试分解求值,例3中的几何体,是由球和棱柱组合而成的,类似的几何体一般称为组合体。指导学生今后组合体问题的求解思路即求组合体的体积(或表面积)时,只需要算出其中每个几何体的体积(或表面积),然后再处理即可.
三、课堂练习,巩固所学
已知一个正三棱锥的四个顶点都在一个球的球面上,而且这个正三棱锥的所有棱长都为2,求这个球的体积.
(课本87页练习B第5题)
参考答案:.
四、归纳总结:
1、台体的体积公式是什么?与柱体、锥体体积公式有什么联系?
2、球体的体积公式是什么?
3、怎样求组合体的体积和表面积?
五.课后作业
教材87页B组第6题;
89页习题11-1A第16题.
教学课时:第2课时
教学目标:
1.、结合学生已经学习掌握的祖暅原理、棱柱棱锥相关知识,推导棱台、球体的体积公式;
2、引导学生解决组合体体积相关问题;
3、提高学生归纳与总结,计算与推理的能力,鼓励学生积极探索体积公式的推导,逐步提高学生数学探究的能力与合作的能力.
教学重点:
棱台和球体积公式的推理过程.
教学难点:
对体积公式的应用和组合体体积问题的解决.
教学过程:
一、提出问题,解决问题:
问题1:上节课我们学过柱体和锥体的体积公式你还记得吗?我们知道,棱台与圆台统称为台体,那么台体的体积可以通过我们已知的知识得到吗?
问题2:已知四棱台上、下底面面积分别为,而且高为h,求这个棱台的体积.
分析:求大小两个锥体的体积还缺少什么量?能用已知量表示吗?
【学生活动1】
分组讨论推导过程并进行小组展示.
问题3:柱体、锥体、台体它们的体积公式之间有怎样的联系?
分析:
【设计意图】
通过学生对柱体、锥体和台体体积公式的结构分析,让学生更清楚的认识到三种几何体之间的联系,帮助学生加深对公式的理解.
问题4:(1)你能想出什么办法测出一个兵乓球的体积?
(2)如图所示是底面积和高都相等的两个几何体,左边是半球,右边是圆柱被挖去一个倒立的圆锥剩余的部分,用平行于半球与圆柱底面的平面去截这两个几何体,所得截面分别是什么形状?两个截面面积大小关系怎样?由此你能得到球的体积公式吗?
分析:半球的截面的面积,是两个圆的面积之差,引引导学生找两个同心圆,从而探索到这个几何体为圆柱中挖去一个等底面积等高的圆锥,从而利用祖暅原理得到:半球的体积=底面半径和高为R圆柱的体积—等底同高的圆锥的体积.
【学生活动2】
分组讨论并进行小组展示.
【设计意图】
让学生通过讨论和结果展示,参与到结论的形成过程中来,从而加深对公式的理解.
拓展:在我国球的体积研究由来已久,公元五、六世纪南北朝时期的祖暅在数学家刘徽的基础上,利用“牟合方盖”和“祖暅原理”推导出了球的体积公式,感兴趣的同学可以参考书后的拓展阅读.
二、例题讲解,深化理解
例(课本85页例3)
如图,某铁制零件由一个正四棱柱和一个球组成,已知正四棱柱底面边长与球的直径均为1cm,正四棱柱的高为2cm,现有这种零件一盒共50kg,取铁的密度为.
(1)估计有多少个这样的零件;
(2)如果要给这盒零件的每个零件表面涂上一种特殊的材料,则需要能涂多少平方厘米的材料(球与接口处的面积不计,结果精确到)?
解:(1)每个零件的体积为
因此每个零件的质量为
因此可估计出零件的个数
(2)每个零件的表面积为
因此零件的表面积之和约为
即需要能涂的材料.
【设计意图】鼓励学生尝试分解求值,例3中的几何体,是由球和棱柱组合而成的,类似的几何体一般称为组合体。指导学生今后组合体问题的求解思路即求组合体的体积(或表面积)时,只需要算出其中每个几何体的体积(或表面积),然后再处理即可.
三、课堂练习,巩固所学
已知一个正三棱锥的四个顶点都在一个球的球面上,而且这个正三棱锥的所有棱长都为2,求这个球的体积.
(课本87页练习B第5题)
参考答案:.
四、归纳总结:
1、台体的体积公式是什么?与柱体、锥体体积公式有什么联系?
2、球体的体积公式是什么?
3、怎样求组合体的体积和表面积?
五.课后作业
教材87页B组第6题;
89页习题11-1A第16题.
