七年级数学7.2.1三角形内角
文档属性
| 名称 | 七年级数学7.2.1三角形内角 |  | |
| 格式 | zip | ||
| 文件大小 | 396.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-23 13:03:19 | ||
图片预览


文档简介
(共17张PPT)
张师傅不小心弄坏了一个三角形模板,现测得有两个角的度数是60°和40°,请问损坏的这个角为几度
想一想
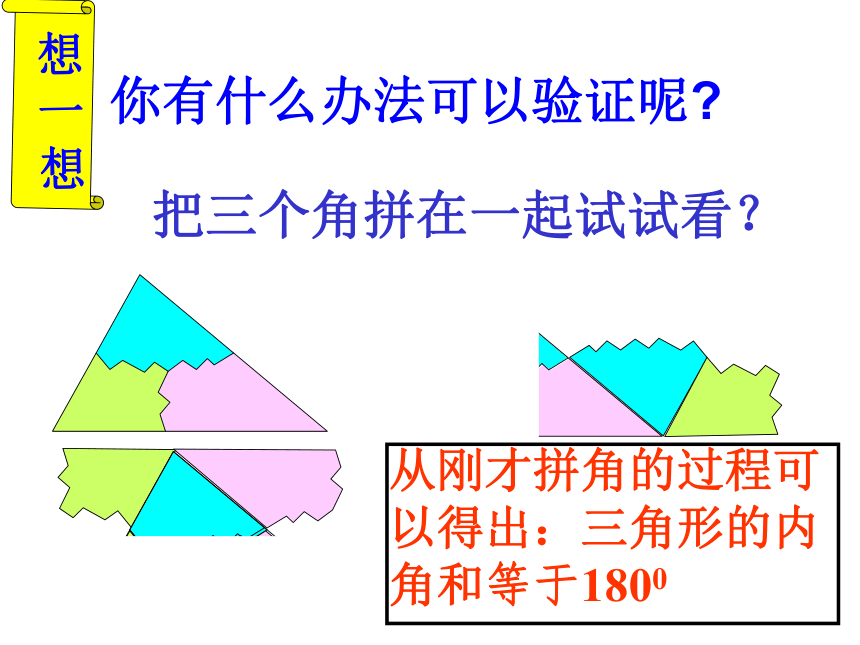
把三个角拼在一起试试看?
你有什么办法可以验证呢
从刚才拼角的过程可 以得出:三角形的内角和等于1800
A
B
C
A
A
A
A
B
B
B
B
B
A
B
C
D
E
1
2
3
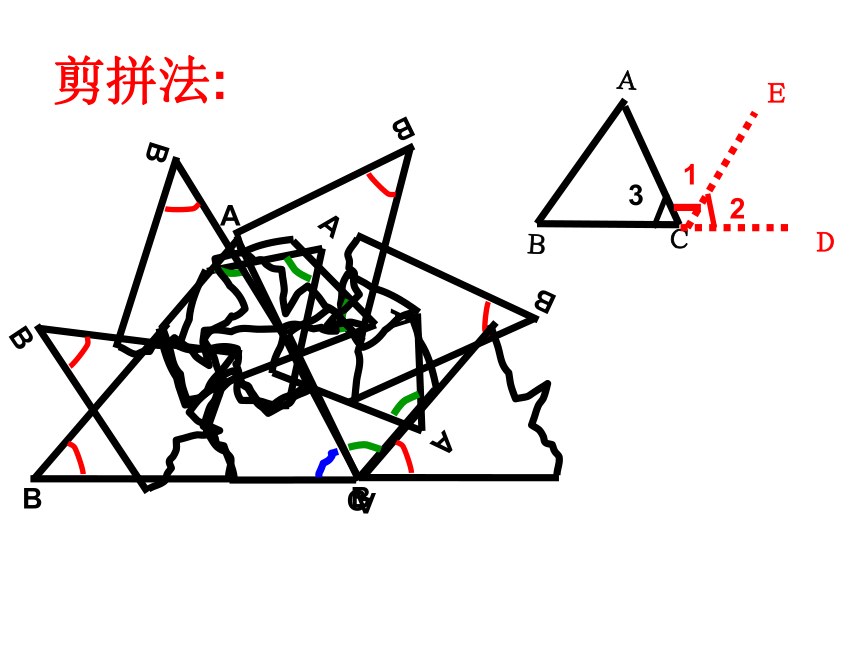
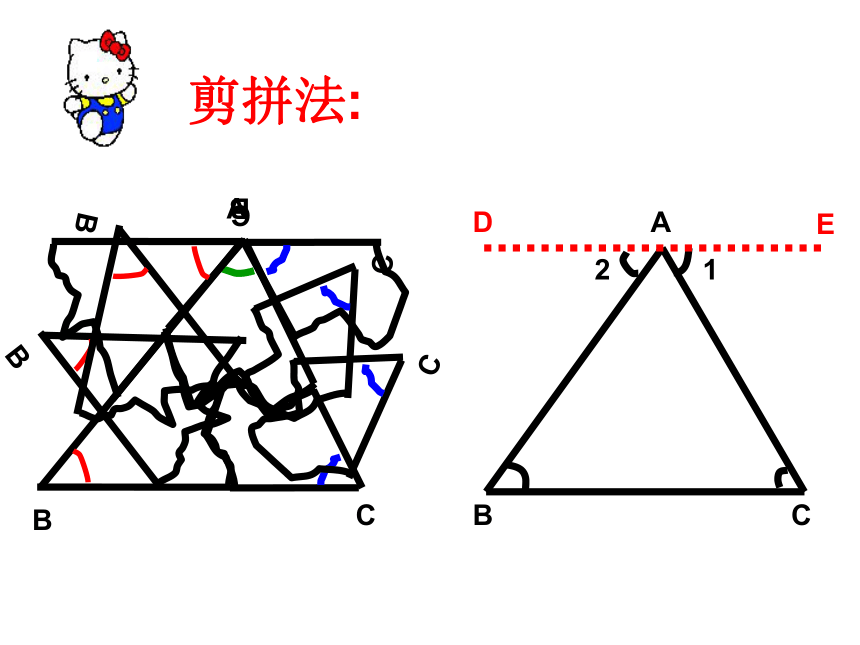
剪拼法:
C
B
A
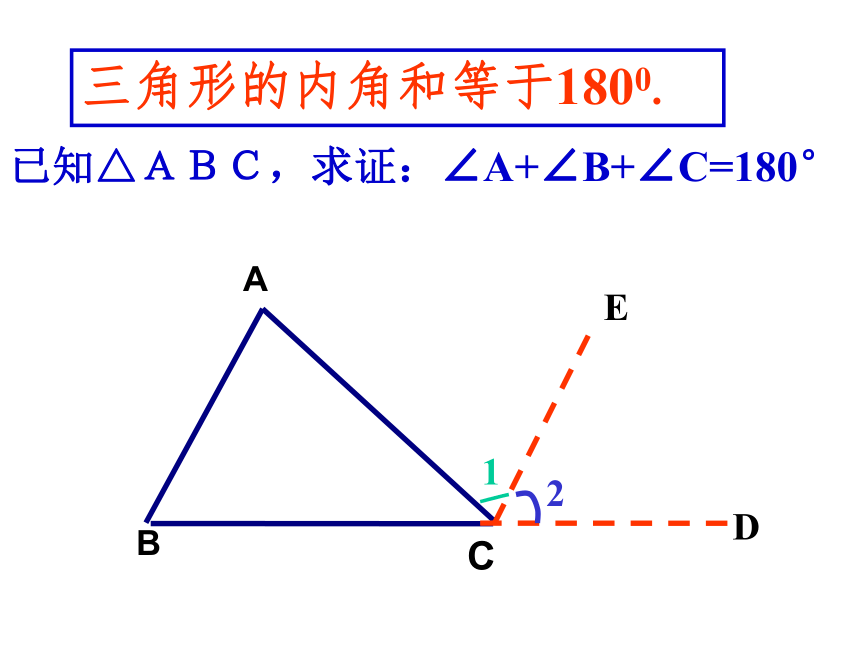
三角形的内角和等于1800.
已知△ABC,求证:∠A+∠B+∠C=180°
1
2
D
E
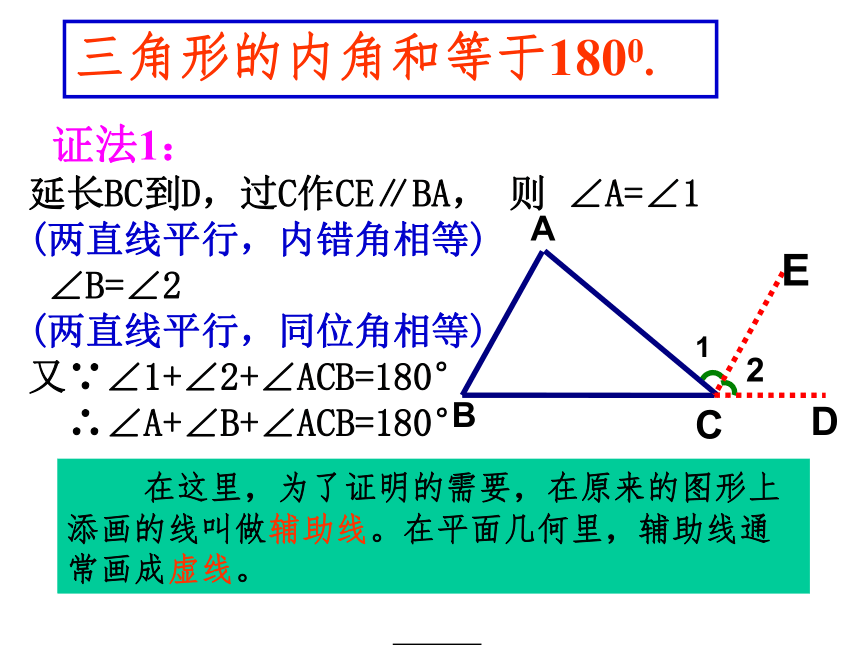
证法1:
延长BC到D,过C作CE∥BA, 则 ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
A
B
C
B
B
B
C
C
C
A
B
C
2
1
D
E
剪拼法:
证法2:过A作EF∥BC,
则∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
三角形的内角和等于1800.
证法3:过A作AE∥BC,
∵ AE∥BC
∴∠B= ∠EAB
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
即∠B+∠C+∠BAC=180°
三角形的内角和等于1800.
C
B
A
E
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
n=
算一算
n
°
80
°
70
°
x
°
x
°
120
°
X=
y=
(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
例题 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从C岛看A、B两岛的视角∠ACB是多少度?
北
.
A
D
北
.
C
B
.
东
E
50°
80 °
40 °
实践操场:
1、(1)在△ABC中,∠A=35°,∠B=43°
则∠ C= .
(2)在△ABC中,∠A :∠B:∠C=2:3:4,则
∠A = ,∠ B= ,
∠ C= .
(3)在△ABC中,∠A=100°,∠B=40°+∠C ,
则∠C= .
(4)在△ABC中,∠B=80°,∠A=3∠C,则
∠A=_________.
102°
80°
60°
40°
20°
75°
2、△ABC中,D是AC延长线上一点,∠A=35° ∠B=65 °则∠BCD度数为( ).
A、80°B、100°
C、65°D、70°
A
C
D
B
B
反馈练习
1.如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A、B两处时视角∠ACB=
2.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°,
则∠C=
A
C
D
B
3、如图,AB∥CD, ∠A=40°,∠D=45°,求∠1和∠2.
C
2
D
1
E
15°
130°
B
A
张师傅不小心弄坏了一个三角形模板,现测得有两个角的度数是60°和40°,请问损坏的这个角为几度
想一想
把三个角拼在一起试试看?
你有什么办法可以验证呢
从刚才拼角的过程可 以得出:三角形的内角和等于1800
A
B
C
A
A
A
A
B
B
B
B
B
A
B
C
D
E
1
2
3
剪拼法:
C
B
A
三角形的内角和等于1800.
已知△ABC,求证:∠A+∠B+∠C=180°
1
2
D
E
证法1:
延长BC到D,过C作CE∥BA, 则 ∠A=∠1
(两直线平行,内错角相等)
∠B=∠2
(两直线平行,同位角相等)
又∵∠1+∠2+∠ACB=180°
∴∠A+∠B+∠ACB=180°
2
1
E
D
C
B
A
三角形的内角和等于1800.
在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线。在平面几何里,辅助线通常画成虚线。
A
B
C
B
B
B
C
C
C
A
B
C
2
1
D
E
剪拼法:
证法2:过A作EF∥BC,
则∠B=∠2
(两直线平行,内错角相等)
∠C=∠1
(两直线平行,内错角相等)
又∵∠2+∠1+∠BAC=180°
∴∠B+∠C+∠BAC=180°
F
2
1
E
C
B
A
三角形的内角和等于1800.
证法3:过A作AE∥BC,
∵ AE∥BC
∴∠B= ∠EAB
(两直线平行,内错角相等)
∠EAB+∠BAC+∠C=180°
(两直线平行,同旁内角互补)
即∠B+∠C+∠BAC=180°
三角形的内角和等于1800.
C
B
A
E
思路总结
为了证明三个角的和为1800,转化为一个平角或同旁内角互补,这种转化思想是数学中的常用方法.
n=
算一算
n
°
80
°
70
°
x
°
x
°
120
°
X=
y=
(1)一个三角形中最多有 个直角?为什么?
(2)一个三角形中最多有 个钝角?为什么?
(3)一个三角形中至少有 个锐角?为什么?
(4)任意 一个三角形中,最大的一个角的度数至少为 .
60°
2
1
1
例题 如图,C岛在A岛的北偏东50°方向,B岛在A岛的北偏东80 °方向,C岛在B岛的北偏西40 °方向。从C岛看A、B两岛的视角∠ACB是多少度?
北
.
A
D
北
.
C
B
.
东
E
50°
80 °
40 °
实践操场:
1、(1)在△ABC中,∠A=35°,∠B=43°
则∠ C= .
(2)在△ABC中,∠A :∠B:∠C=2:3:4,则
∠A = ,∠ B= ,
∠ C= .
(3)在△ABC中,∠A=100°,∠B=40°+∠C ,
则∠C= .
(4)在△ABC中,∠B=80°,∠A=3∠C,则
∠A=_________.
102°
80°
60°
40°
20°
75°
2、△ABC中,D是AC延长线上一点,∠A=35° ∠B=65 °则∠BCD度数为( ).
A、80°B、100°
C、65°D、70°
A
C
D
B
B
反馈练习
1.如图,从A处观测C处的仰角∠CAD=30°,从B处观测C处的仰角∠CBD=45°,从C处观测A、B两处时视角∠ACB=
2.如图,一种滑翔伞的形状是左右对称的四边形ABCD,其中∠A=150°,∠B=∠D=40°,
则∠C=
A
C
D
B
3、如图,AB∥CD, ∠A=40°,∠D=45°,求∠1和∠2.
C
2
D
1
E
15°
130°
B
A
