沪科版八年级上册数学课件-12.4 综合与实践 一次函数模型的应用 (23张PPT)
文档属性
| 名称 | 沪科版八年级上册数学课件-12.4 综合与实践 一次函数模型的应用 (23张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 00:00:00 | ||
图片预览






文档简介
12.4 综合与实践 一次函数模型的应用
沪科版·八年级上册
新课导入
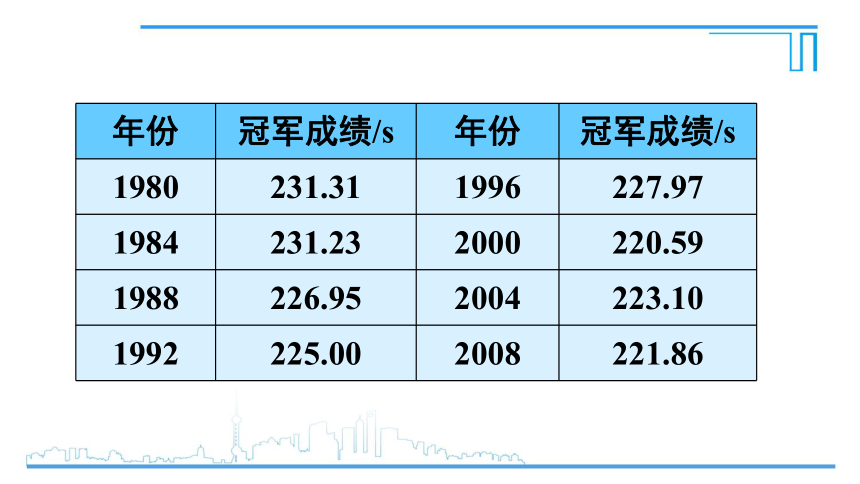
问题 奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400m自由泳项目,1996年奥运会冠军的成绩比1960年提高了约30s.下面是该项目冠军的一些数据:
1
年份
冠军成绩/s
年份
冠军成绩/s
1980
231.31
1996
227.97
1984
231.23
2000
220.59
1988
226.95
2004
223.10
1992
225.00
2008
221.86
新课推进
根据上面资料,能否估计2012年伦敦奥运会时该项目的冠军成绩?
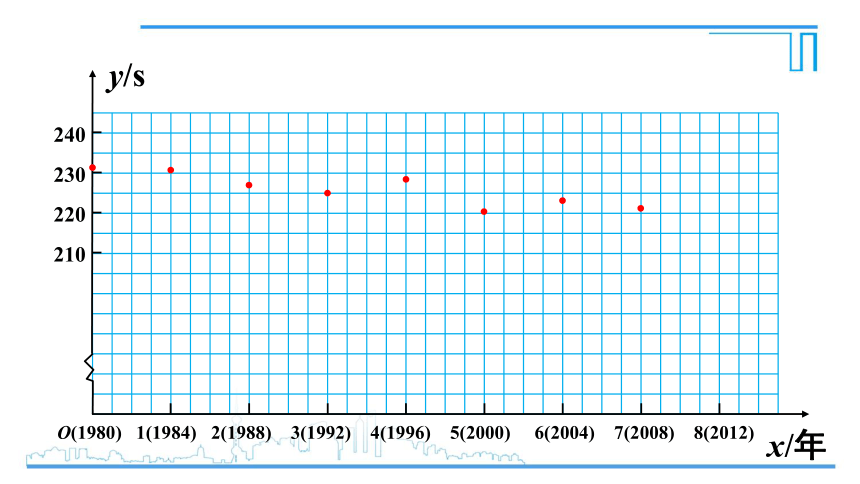
(1)建立如下图所示的坐标系并描点;
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
?
?
?
?
?
?
?
?
(2)根据图中描出点的分布情况,根据已知条件来猜测x与y之间的函数形式(或“近似”的函数形式),并写出表达式;
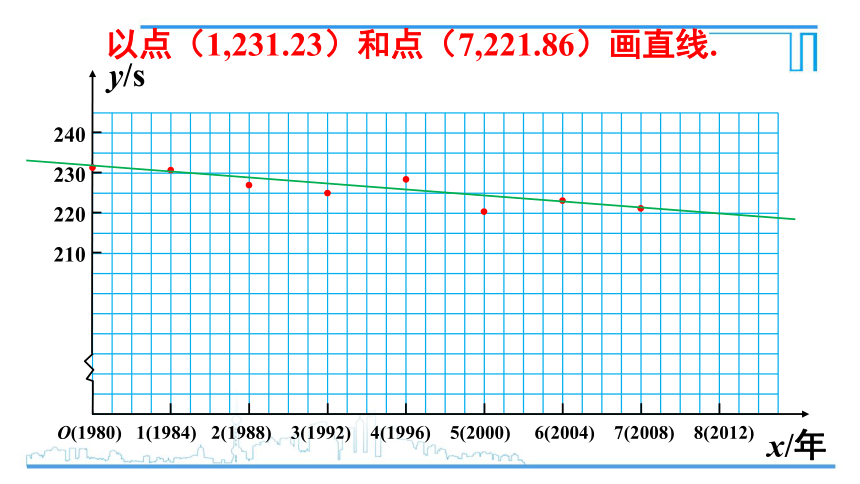
要确定一个一次函数表达式,只要知道两点坐标即可.这里,选哪两点呢?
用一个透明的三角尺,让它的一条边通过图中8个点中任意两点,直观地比较看,选择其中哪两点时,其余点更靠近直尺的这条边,或者这条边的上、下个数大体差不多.
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
?
?
?
?
?
?
?
?
以点(1,231.23)和点(7,221.86)画直线.
(3)根据你建立的模型,估计2012年伦敦奥运会该项目的冠军成绩;
直线的表达式:y=-1.56x+232.79
当x=8时,y=220.31
2012年伦敦奥运会中国选手孙杨以220.14s成为冠军.
220.31s接近220.14s.
(4)能否用上述模型预测2016年里约热内卢奥运会该项目的冠军成绩?
通过本例,使我们认识到可以利用所学知识去研究一些不确定现象之间的规律性,这里用“直线”来模拟发展趋势的问题.
建立两个变量之间的函数模型,可以通过下列几个步骤完成:
将实验得到的数据在直角坐标系中描出;
观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
进行检验;
应用这个函数模型解决问题.
1
2
3
4
问题 球从高处下落再反弹起来,可以直观地看出球的下落高度越高,反弹高度也就越高,那么球下落高度与反弹高度具有怎样的关系呢?请你进行实验,将实验数据填入下表,并根据实验数据建立球下落高度和反弹高度之间关系的函数模型.
2
实验次数
第1次
第2次
第3次
第4次
第5次
第6次
下落高度/cm
反弹高度/cm
问题 请你选择一个可以应用函数模型解决的问题,并建立合适的函数模型.
3
随堂演练
1.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:
指距x(cm)
19
20
21
身高y(cm)
151
160
169
(1) 求身高y与指距x之间的函数表达式;
解 上表3组数据反映了身高y与指距x之间的对应关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以尝试建立一次函数模型.
指距x(cm)
19
20
21
身高y(cm)
151
160
169
设身高y与指距x之间的函数表达式为y = kx + b.
将x=19, y=151与x = 20,y=160代入上式,得
19k + b = 151,
20k + b = 160.
得到 y = 9x -20.
解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.
(2) 当李华的指距为22cm时,你能预测他的身高吗?
2.在某地,人们发现某种蟋蟀1min 所叫次数与当地气温之间近似为一次函数关系. 下面是蟋蟀所叫次数与气温变化情况对照表:
蟋蟀叫的次数
…
84
98
119
…
温度(℃)
…
15
17
20
…
(1)根据表中数据确定该一次函数的表达式;
(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约为多少摄氏度?
(3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的次数吗?
蟋蟀叫的次数
…
84
98
119
…
温度(℃)
…
15
17
20
…
解(1)设蟋蟀1min所叫次数与气温之间的函数表达式为y = kx + b. 将x=15, y=84与x = 20,y=119代入上式,得
15k + b = 84,
20k + b = 119.
解得k = 7, b = -21.
于是y = 7x -21.
有y = 7x -21=63,
解得x=12.
(2)当y = 63时,
解
(3)不能,因为此函数关系是近似的,与实际生活中的情况有所不符,蟋蟀在0 ℃时可能不会鸣叫.
沪科版·八年级上册
新课导入
问题 奥运会每4年举办一次,奥运会的游泳记录在不断地被突破,如男子400m自由泳项目,1996年奥运会冠军的成绩比1960年提高了约30s.下面是该项目冠军的一些数据:
1
年份
冠军成绩/s
年份
冠军成绩/s
1980
231.31
1996
227.97
1984
231.23
2000
220.59
1988
226.95
2004
223.10
1992
225.00
2008
221.86
新课推进
根据上面资料,能否估计2012年伦敦奥运会时该项目的冠军成绩?
(1)建立如下图所示的坐标系并描点;
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
?
?
?
?
?
?
?
?
(2)根据图中描出点的分布情况,根据已知条件来猜测x与y之间的函数形式(或“近似”的函数形式),并写出表达式;
要确定一个一次函数表达式,只要知道两点坐标即可.这里,选哪两点呢?
用一个透明的三角尺,让它的一条边通过图中8个点中任意两点,直观地比较看,选择其中哪两点时,其余点更靠近直尺的这条边,或者这条边的上、下个数大体差不多.
x/年
y/s
240
230
220
210
O(1980) 1(1984) 2(1988) 3(1992) 4(1996) 5(2000) 6(2004) 7(2008) 8(2012)
?
?
?
?
?
?
?
?
以点(1,231.23)和点(7,221.86)画直线.
(3)根据你建立的模型,估计2012年伦敦奥运会该项目的冠军成绩;
直线的表达式:y=-1.56x+232.79
当x=8时,y=220.31
2012年伦敦奥运会中国选手孙杨以220.14s成为冠军.
220.31s接近220.14s.
(4)能否用上述模型预测2016年里约热内卢奥运会该项目的冠军成绩?
通过本例,使我们认识到可以利用所学知识去研究一些不确定现象之间的规律性,这里用“直线”来模拟发展趋势的问题.
建立两个变量之间的函数模型,可以通过下列几个步骤完成:
将实验得到的数据在直角坐标系中描出;
观察这些点的特征,确定选用的函数形式,并根据已知数据求出具体的函数表达式;
进行检验;
应用这个函数模型解决问题.
1
2
3
4
问题 球从高处下落再反弹起来,可以直观地看出球的下落高度越高,反弹高度也就越高,那么球下落高度与反弹高度具有怎样的关系呢?请你进行实验,将实验数据填入下表,并根据实验数据建立球下落高度和反弹高度之间关系的函数模型.
2
实验次数
第1次
第2次
第3次
第4次
第5次
第6次
下落高度/cm
反弹高度/cm
问题 请你选择一个可以应用函数模型解决的问题,并建立合适的函数模型.
3
随堂演练
1.请每位同学伸出一只手掌,把大拇指与小拇指尽量张开,两指间的距离称为指距. 已知指距与身高具有如下关系:
指距x(cm)
19
20
21
身高y(cm)
151
160
169
(1) 求身高y与指距x之间的函数表达式;
解 上表3组数据反映了身高y与指距x之间的对应关系,观察这两个变量之间的变化规律,当指距增加1cm,身高就增加9cm,可以尝试建立一次函数模型.
指距x(cm)
19
20
21
身高y(cm)
151
160
169
设身高y与指距x之间的函数表达式为y = kx + b.
将x=19, y=151与x = 20,y=160代入上式,得
19k + b = 151,
20k + b = 160.
得到 y = 9x -20.
解 当x = 22时, y = 9×22-20 = 178.
因此,李华的身高大约是178 cm.
(2) 当李华的指距为22cm时,你能预测他的身高吗?
2.在某地,人们发现某种蟋蟀1min 所叫次数与当地气温之间近似为一次函数关系. 下面是蟋蟀所叫次数与气温变化情况对照表:
蟋蟀叫的次数
…
84
98
119
…
温度(℃)
…
15
17
20
…
(1)根据表中数据确定该一次函数的表达式;
(2)如果蟋蟀1min叫了63次,那么该地当时的气温大约为多少摄氏度?
(3)能用所求出的函数模型来预测蟋蟀在0 ℃时所鸣叫的次数吗?
蟋蟀叫的次数
…
84
98
119
…
温度(℃)
…
15
17
20
…
解(1)设蟋蟀1min所叫次数与气温之间的函数表达式为y = kx + b. 将x=15, y=84与x = 20,y=119代入上式,得
15k + b = 84,
20k + b = 119.
解得k = 7, b = -21.
于是y = 7x -21.
有y = 7x -21=63,
解得x=12.
(2)当y = 63时,
解
(3)不能,因为此函数关系是近似的,与实际生活中的情况有所不符,蟋蟀在0 ℃时可能不会鸣叫.
