七年级数学7.3.2多边形的内角和与外角和
文档属性
| 名称 | 七年级数学7.3.2多边形的内角和与外角和 |

|
|
| 格式 | zip | ||
| 文件大小 | 223.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-04-23 00:00:00 | ||
图片预览



文档简介
(共19张PPT)
1、从n边形的一个顶点可以引_____对角线
将n边形分成了________个三角形。
2、n边形的对角线一共有______条。
(n-3)
(n-2)
温故知新
3、三角形的内角和等于 ____,外角和等____。
180○
360○
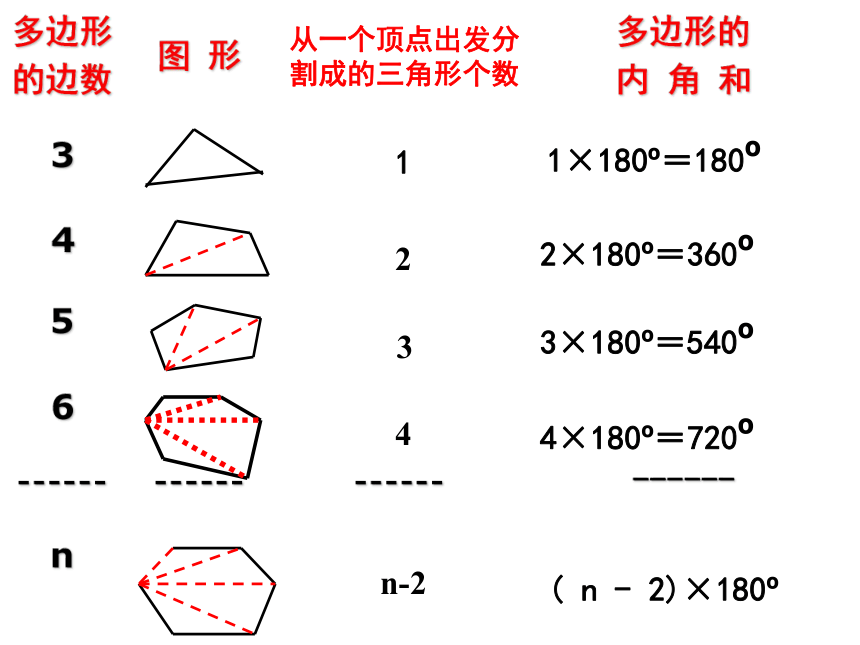
多边形
的边数 图 形 多边形的
内 角 和
3
4
5
6
------ ------ ------ ------
n
n-2
1
2
3
1×180 =180
从一个顶点出发分割成的三角形个数
2×180 =360
3×180 =540
( n - 2)×180
4
4×180 =720
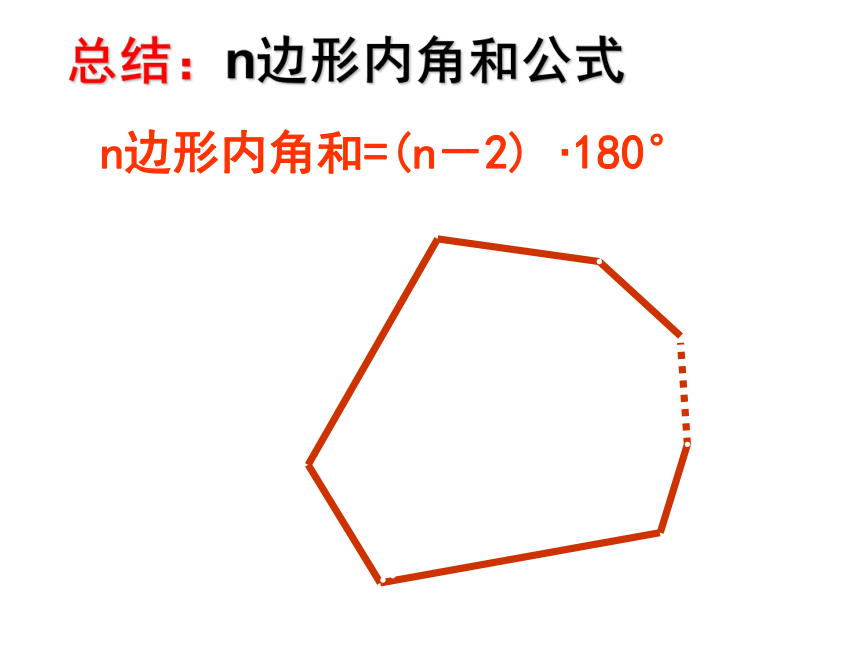
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
A
E
D
C
B
O
1
5
4
3
2
A
E
D
C
B
O
1
2
3
4
A
B
C
D
E
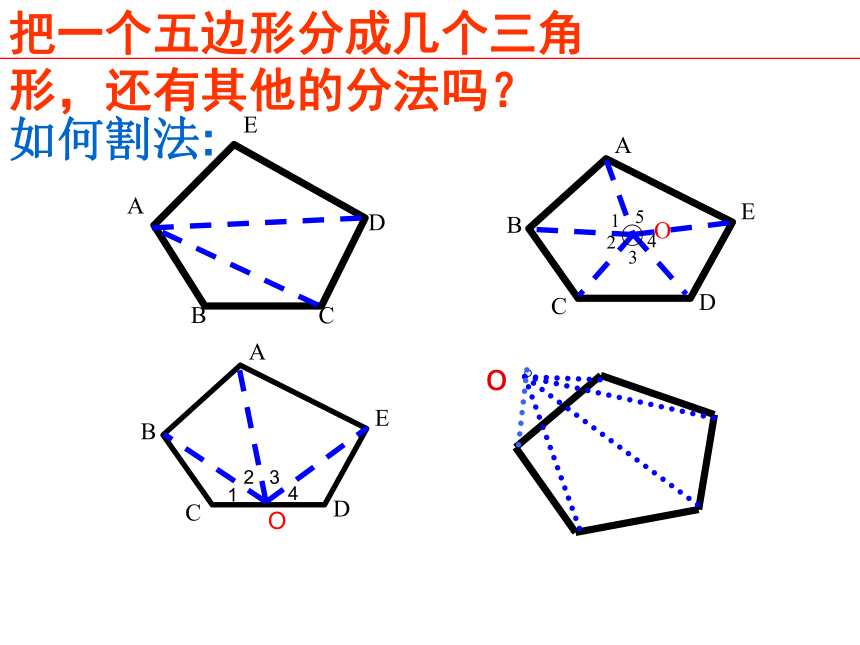
如何割法:
o
把一个五边形分成几个三角形,还有其他的分法吗?
练习:
1、八边形的内角和是( )
2、十二边形的内角和是( )
3、正十边形的内角和是( ),每个内角是( )
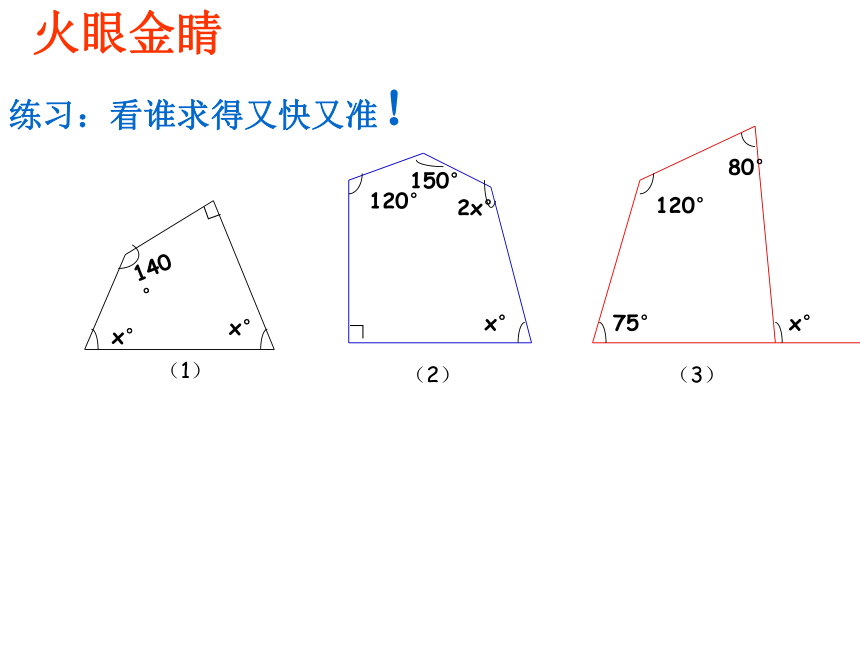
练习:看谁求得又快又准!
x°
140°
∟
x°
(1)
∟
120°
150°
2x°
x°
120°
80°
75°
x°
火眼金睛
(2)
(3)
例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
6
E
B
C
D
1
2
3
4
5
A
探究 如果将例2中五边形换成n边(n≥3)
可以得到同样的结果吗?
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
例:
一个多边形的内角和1080°,它是几边形?
练习. 已知一个多边形,它的内角和等于外角和,它是几边形?
练一练
练习1:如果一个多边形的每一个外角都等于30°,则这个多边形的边数是_____。
12
练一练
练习2:正五边形的每一个外角等于____,每一个内角等于_____。
72°
144°
1、n边形的内角和等于__________,九边形的内角和等于___________。
2、一个多边形当边数增加1时,它的内角和增加( )。
3、已知多边形的每个内角都等于150°,求这个多边形的边数?
4、一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A:360° B:540° C:720° D:900°
5. 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
n边形内角和=(n-2) ·180°
n边形外角和=360°
n边形外角和= n个平角-n边形内角和
通过这节课的学习你有哪些收获?
1、从n边形的一个顶点可以引_____对角线
将n边形分成了________个三角形。
2、n边形的对角线一共有______条。
(n-3)
(n-2)
温故知新
3、三角形的内角和等于 ____,外角和等____。
180○
360○
多边形
的边数 图 形 多边形的
内 角 和
3
4
5
6
------ ------ ------ ------
n
n-2
1
2
3
1×180 =180
从一个顶点出发分割成的三角形个数
2×180 =360
3×180 =540
( n - 2)×180
4
4×180 =720
总结:n边形内角和公式
B
A
C
D
G
F
E
n边形内角和=(n-2) ·180°
A
E
D
C
B
O
1
5
4
3
2
A
E
D
C
B
O
1
2
3
4
A
B
C
D
E
如何割法:
o
把一个五边形分成几个三角形,还有其他的分法吗?
练习:
1、八边形的内角和是( )
2、十二边形的内角和是( )
3、正十边形的内角和是( ),每个内角是( )
练习:看谁求得又快又准!
x°
140°
∟
x°
(1)
∟
120°
150°
2x°
x°
120°
80°
75°
x°
火眼金睛
(2)
(3)
例1:已知四边形ABCD,∠A+∠C=180°,求∠B+∠D=?
A
B
C
D
例2 如图,在五边形的每个顶点处各取一个外角,这些外角的和叫做五边形的外角和.五边形的外角和等于多少?
6
E
B
C
D
1
2
3
4
5
A
探究 如果将例2中五边形换成n边(n≥3)
可以得到同样的结果吗?
n边形外角和=
结论:
n边形的外角和等于360°
-(n-2) × 180°
=360 °
A
1
E
B
C
D
2
3
4
5
F
n
n个平角-n边形内角和
=n×180 °
从多边形的一个顶点A点出发,沿多边形的各边走过各点之后回到点A.最后再转回出发时的方向。在行程中所转的各个角的和,就是多边形的外角和。
例:
一个多边形的内角和1080°,它是几边形?
练习. 已知一个多边形,它的内角和等于外角和,它是几边形?
练一练
练习1:如果一个多边形的每一个外角都等于30°,则这个多边形的边数是_____。
12
练一练
练习2:正五边形的每一个外角等于____,每一个内角等于_____。
72°
144°
1、n边形的内角和等于__________,九边形的内角和等于___________。
2、一个多边形当边数增加1时,它的内角和增加( )。
3、已知多边形的每个内角都等于150°,求这个多边形的边数?
4、一个多边形从一个顶点可引对角线3条,这个多边形内角和等于( )
A:360° B:540° C:720° D:900°
5. 已知一个多边形,它的内角和等于外角和的2倍,求这个多边形的边数?
n边形内角和=(n-2) ·180°
n边形外角和=360°
n边形外角和= n个平角-n边形内角和
通过这节课的学习你有哪些收获?
