沪科版八年级上册数学课件-13.1.2 三角形中角的关系 (20张PPT)
文档属性
| 名称 | 沪科版八年级上册数学课件-13.1.2 三角形中角的关系 (20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 500.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 21:10:04 | ||
图片预览


文档简介
第2课时 三角形中角的关系
沪科版 八年级上册
锐角三角形
三个角都是锐角的三角形
A
B
C
直角三角形
有一个角是直角的三角形
A
B
C
钝角三角形
有一个角是钝角的三角形
A
B
C
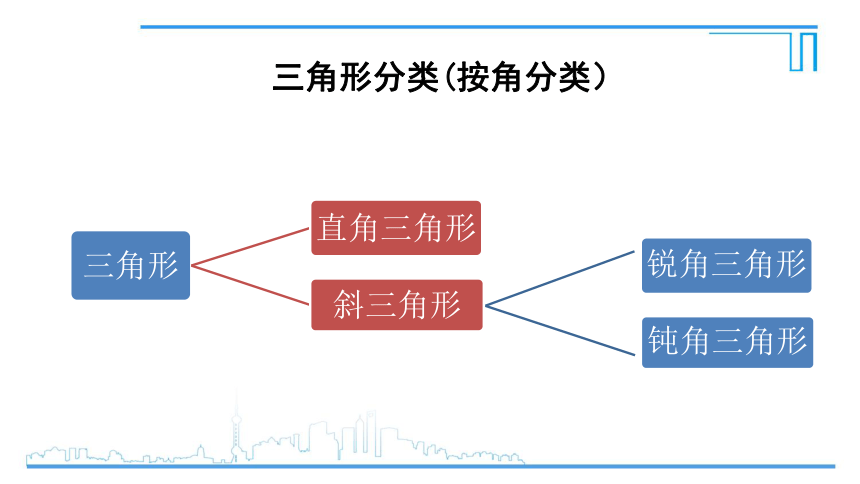
三角形分类(按角分类)
锐角三角形
钝角三角形
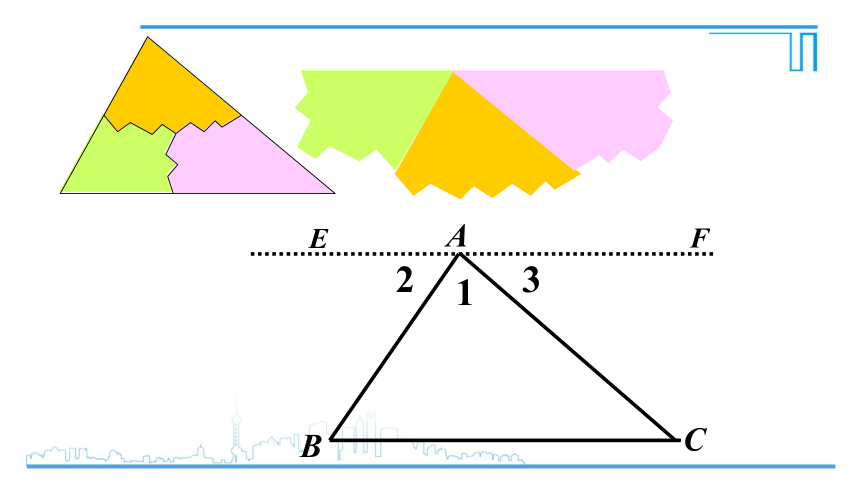
三角形的三个内角和是多少?
有什么办法可以验证呢?
A
B
C
A
B
C
1
2
3
E
F
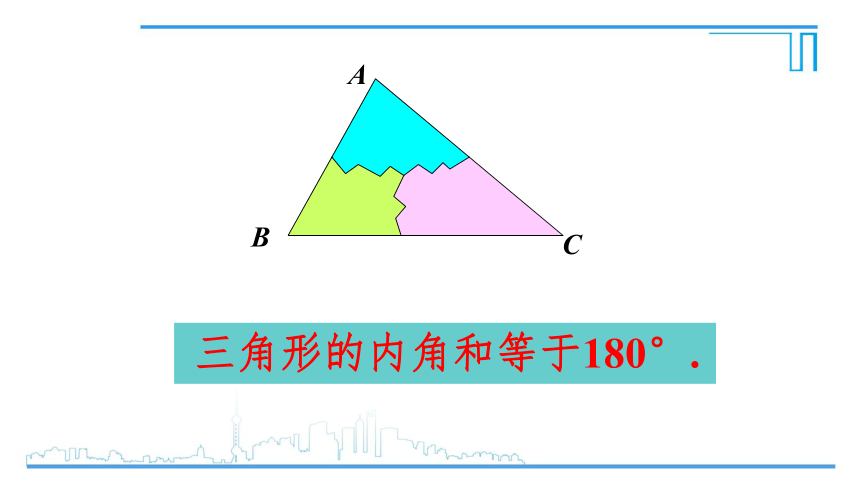
三角形的内角和等于180°.
A
B
C
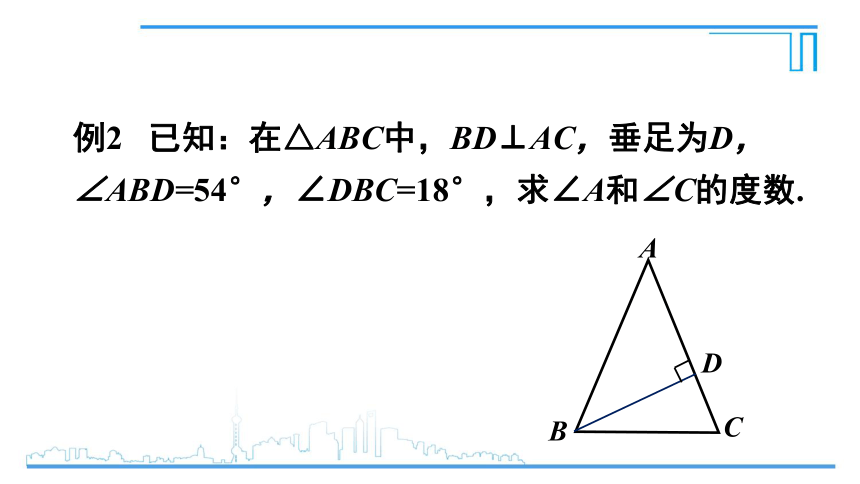
例2 已知:在△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A和∠C的度数.
A
B
C
D
解:因为 BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,∠A+ ∠ABD+ ∠ADB=180 °, (三角形的内角和等于180°)
∠ABD=54°, ∠ADB=90°,(已知)
∠A=180°-∠ABD-∠ADB
=180°-54°-90°=36°.
在△ABC中,
∠C=180°-∠A-(∠ABD+∠DBC)
=180°-36°-(54°+18°)=72°.
A
B
C
D
1. 在△ABC中:
(1)已知:∠A=105°,∠B-∠C= 15°,则∠C= ;
(2)已知:∠A:∠B:∠C=3:4:5,则∠C= ;
30°
75°
2. 已知:如图,∠ACB=90°,CD⊥AB,垂足是D.
(1)写出图中所有相等的角;
(2)写出图中所有直角三角形,并指出它们的斜边.
A
B
C
D
3. 已知:如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC=46°.求∠CAD的度数.
A
B
C
D
A
B
C
D
解:∵AD⊥BC,∴∠BDA=90°,
∴∠BAD=180°-90°-70°=20°,
又∵∠BAC=46°,
∴∠CAD=46°-20°=26°
1. 在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
2. 在△ABC中, ∠A :∠B:∠C=2:3:4则∠A = ∠ B= ∠ C= .
102 °
80 °
60 °
40 °
3. 如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去
(C)带③去 (D)带①和②去
C
4. 在△ABC中,已知∠A-∠C=25°,∠B-∠A=10°,求∠B的度数.
分析:根据三角形内角和定理可知: ∠A+∠B+∠C=180°,然后结合已知条件便可以求出.
解:在△ABC中,
∠A+∠B+∠C=180°(三角形内角和定理)
联立∠A-∠C=25°,∠B-∠A=10°可得,
∠A=65°,∠B=75°,∠C=40°
答:∠B的度数是75°.
三角形内角和定理:
三角形的内角和等于180°.
为了说明三个角的和为180°,转化为一个平角,转化思想是数学中的常用方法.
1.从教材习题中选取,
2.完成练习册本课时的习题.
沪科版 八年级上册
锐角三角形
三个角都是锐角的三角形
A
B
C
直角三角形
有一个角是直角的三角形
A
B
C
钝角三角形
有一个角是钝角的三角形
A
B
C
三角形分类(按角分类)
锐角三角形
钝角三角形
三角形的三个内角和是多少?
有什么办法可以验证呢?
A
B
C
A
B
C
1
2
3
E
F
三角形的内角和等于180°.
A
B
C
例2 已知:在△ABC中,BD⊥AC,垂足为D,∠ABD=54°,∠DBC=18°,求∠A和∠C的度数.
A
B
C
D
解:因为 BD⊥AC,(已知)
所以∠ADB=∠CDB=90°.
在△ABD中,∠A+ ∠ABD+ ∠ADB=180 °, (三角形的内角和等于180°)
∠ABD=54°, ∠ADB=90°,(已知)
∠A=180°-∠ABD-∠ADB
=180°-54°-90°=36°.
在△ABC中,
∠C=180°-∠A-(∠ABD+∠DBC)
=180°-36°-(54°+18°)=72°.
A
B
C
D
1. 在△ABC中:
(1)已知:∠A=105°,∠B-∠C= 15°,则∠C= ;
(2)已知:∠A:∠B:∠C=3:4:5,则∠C= ;
30°
75°
2. 已知:如图,∠ACB=90°,CD⊥AB,垂足是D.
(1)写出图中所有相等的角;
(2)写出图中所有直角三角形,并指出它们的斜边.
A
B
C
D
3. 已知:如图,在△ABC中,AD⊥BC,垂足是D,∠B=70°,∠BAC=46°.求∠CAD的度数.
A
B
C
D
A
B
C
D
解:∵AD⊥BC,∴∠BDA=90°,
∴∠BAD=180°-90°-70°=20°,
又∵∠BAC=46°,
∴∠CAD=46°-20°=26°
1. 在△ABC中,∠A=35°,∠ B=43 °
则∠ C= .
2. 在△ABC中, ∠A :∠B:∠C=2:3:4则∠A = ∠ B= ∠ C= .
102 °
80 °
60 °
40 °
3. 如图,某同学把一块三角形的玻璃打碎成三片,现在他要到玻璃店去配一块形状完全一样的玻璃,那么最省事的办法是 ( )
(A)带①去 (B)带②去
(C)带③去 (D)带①和②去
C
4. 在△ABC中,已知∠A-∠C=25°,∠B-∠A=10°,求∠B的度数.
分析:根据三角形内角和定理可知: ∠A+∠B+∠C=180°,然后结合已知条件便可以求出.
解:在△ABC中,
∠A+∠B+∠C=180°(三角形内角和定理)
联立∠A-∠C=25°,∠B-∠A=10°可得,
∠A=65°,∠B=75°,∠C=40°
答:∠B的度数是75°.
三角形内角和定理:
三角形的内角和等于180°.
为了说明三个角的和为180°,转化为一个平角,转化思想是数学中的常用方法.
1.从教材习题中选取,
2.完成练习册本课时的习题.
