七年级数学7.4镶嵌
图片预览








文档简介
(共29张PPT)
复习巩固
1、正三角形的一个外角是( ),一个内角是( )
2、正五边形的一个外角是( ),一个内角是( )
3、正六边形的一个外角是( ),一个内角是( )
4、正八边形的一个外角是( ),一个内角是( )
根河一中 张建军
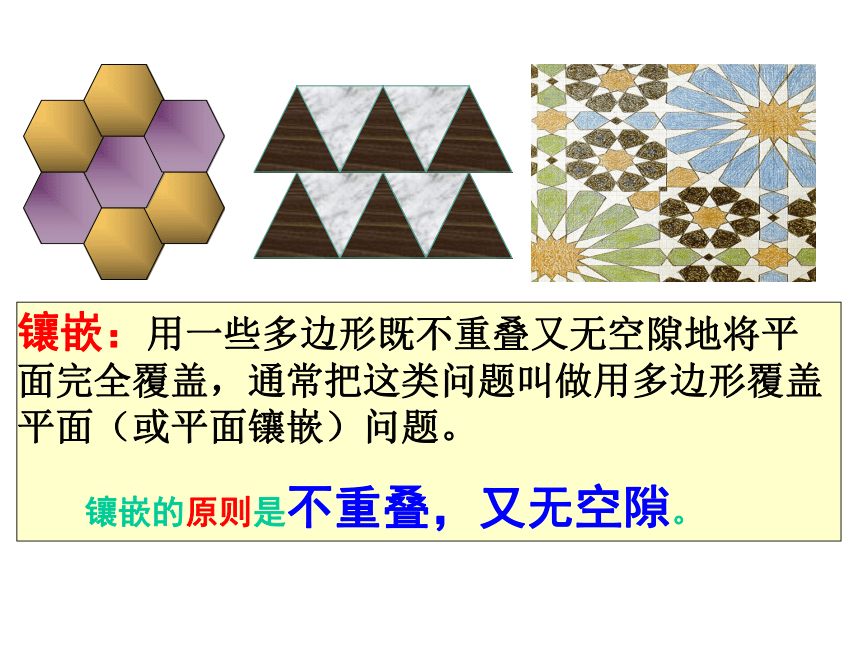
镶嵌:用一些多边形既不重叠又无空隙地将平面完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)问题。
镶嵌的原则是不重叠,又无空隙。
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
理一理
6
60
0
90
0
108
0
120
0
4
3
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
108 ×3<360
0
0
120 ×3=360
0
0
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =5
n = 6
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
1、正三角形与正方形的镶嵌:
拼拼看
拼拼看
2、正三角形与正六边形的镶嵌:
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
4、 下列正多边形的组合中 , 不能镶嵌的是 ( ) A. 正方形和正三角形 B. 正方形和正八边形 C. 正三角形和正十二边形 D. 正方形和正六边形
1、下列正多边形不能够镶嵌成平面图案的是 ( ) A 正三角形 B 正方形 C 正五边形 D 正六边形
2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的
正方形的个数是( )
A、 3 B 、4 C、5 D 、6
3、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形
的每一个顶点周围都有6个正多边形,则该正多边形的内角度数
为( )
A、120 0 B、90 0 C、60 0 D、450
知识检测:
C
C
B
D
知识归纳:
多边形能进行平面镶嵌的条件:
(1)拼接在同一点的各个角的度数和是3600;
(2)相邻的多边形有公共边。
课外作业:
请同学们设计一个平面镶嵌图形:
要求:
1、如果用正多边形镶嵌,设计时必须用两种(或两种以上)正多边形镶嵌。
2、也可以用不规则的图形,设计丰富多采的镶嵌图案。
方法:
可用用彩纸拼,也可自己画。
复习巩固
1、正三角形的一个外角是( ),一个内角是( )
2、正五边形的一个外角是( ),一个内角是( )
3、正六边形的一个外角是( ),一个内角是( )
4、正八边形的一个外角是( ),一个内角是( )
根河一中 张建军
镶嵌:用一些多边形既不重叠又无空隙地将平面完全覆盖,通常把这类问题叫做用多边形覆盖平面(或平面镶嵌)问题。
镶嵌的原则是不重叠,又无空隙。
探究1:仅用一种正多边形镶嵌,哪些正多边形能单独镶嵌成一个平面图案?
正方形
正三角形
正六边形
做一做:
啊!拼不了啦,为什么呢 你能说说道理吗
1
2
3
∠1+∠2+∠3=
用边长相同的正五边形能否镶嵌?
理一理
6
60
0
90
0
108
0
120
0
4
3
3
能拼好
能拼好
不能拼好
有缺口
能拼好
60 ×6=360
0
0
90 ×4=360
0
0
108 ×3<360
0
0
120 ×3=360
0
0
实 验 结 果
正n边形
拼图
每个内角度数
多边形个数
结果
n = 3
n = 4
n =5
n = 6
探究2:用边长相等的两种正多边形镶嵌,哪两种正多边形能镶嵌成一个平面图案?
1、正三角形与正方形的镶嵌:
拼拼看
拼拼看
2、正三角形与正六边形的镶嵌:
想一想
正方形和正八边形能否镶嵌
正三角形和正十二边形能否镶嵌
探究3:
用几个形状、大小相同的任意三角形能镶嵌成一个平面图案吗?四边形呢?
1
3
2
1
4
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
∵ ∠1+∠2+∠3=180°
∴2(∠1+∠2+∠3)=360°
任意三角形能镶嵌成平面图案。
因为∠1+∠2+∠3+∠4=360°
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
1
4
3
2
所以任意四边形能镶嵌成平面图案。
多边形镶嵌的条件:
拼接在同一个顶点处的各个多边形的内角之和等于360°
4、 下列正多边形的组合中 , 不能镶嵌的是 ( ) A. 正方形和正三角形 B. 正方形和正八边形 C. 正三角形和正十二边形 D. 正方形和正六边形
1、下列正多边形不能够镶嵌成平面图案的是 ( ) A 正三角形 B 正方形 C 正五边形 D 正六边形
2、用正方形一种图形进行平面镶嵌时,在它的一个顶点周围的
正方形的个数是( )
A、 3 B 、4 C、5 D 、6
3、如果只用一种正多边形作平面镶嵌,而且在每一个正多边形
的每一个顶点周围都有6个正多边形,则该正多边形的内角度数
为( )
A、120 0 B、90 0 C、60 0 D、450
知识检测:
C
C
B
D
知识归纳:
多边形能进行平面镶嵌的条件:
(1)拼接在同一点的各个角的度数和是3600;
(2)相邻的多边形有公共边。
课外作业:
请同学们设计一个平面镶嵌图形:
要求:
1、如果用正多边形镶嵌,设计时必须用两种(或两种以上)正多边形镶嵌。
2、也可以用不规则的图形,设计丰富多采的镶嵌图案。
方法:
可用用彩纸拼,也可自己画。
