七年级数学三角形的外角
图片预览



文档简介
(共24张PPT)
民勤二中 马正平
三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B= ,∠C= ,
40°
60°
80°
65°
60°
A
B
C
D
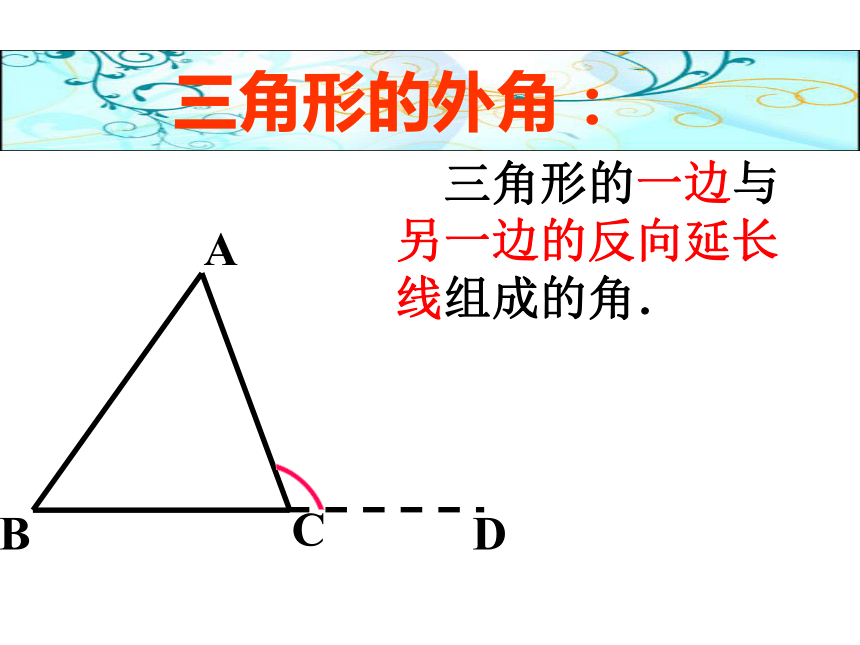
三角形的外角:
三角形的一边与另一边的反向延长线组成的角.
A
B
C
D
E
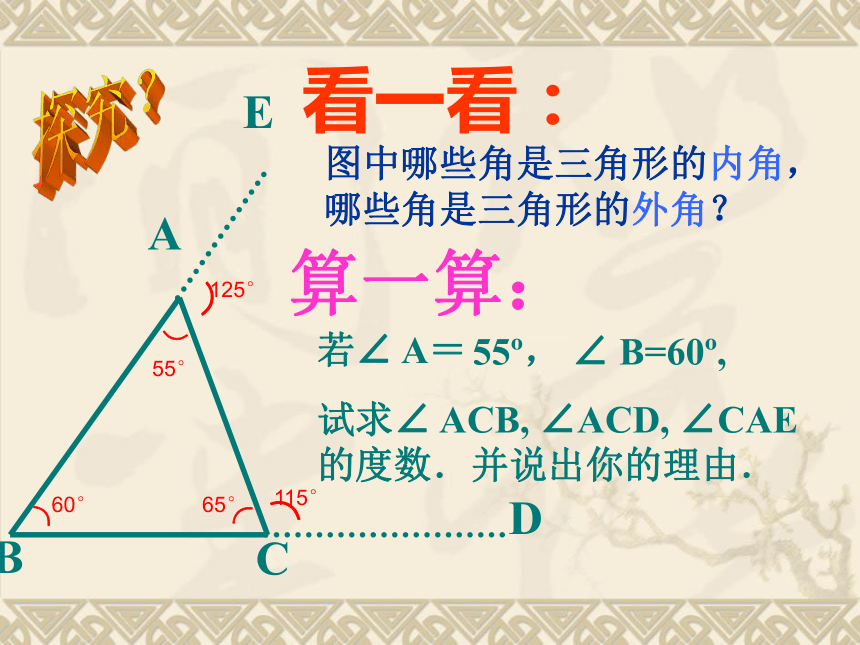
看一看:
算一算:
若∠ A=
55 , ∠ B=60 ,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
通过上题的计算,你发现∠ACD, ∠ CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
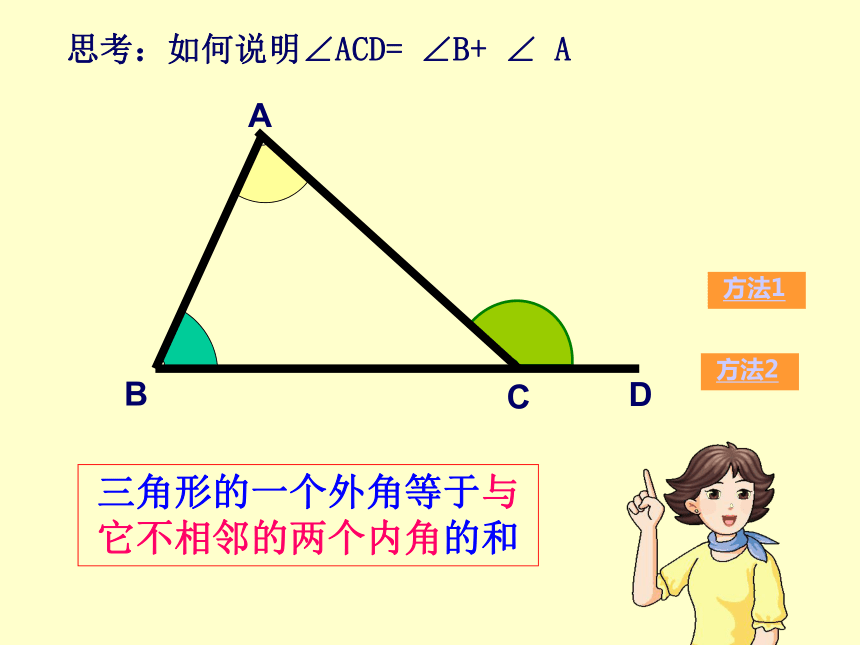
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
方法1
方法2
三角形的一个外角等于与它不相邻的两个内角的和
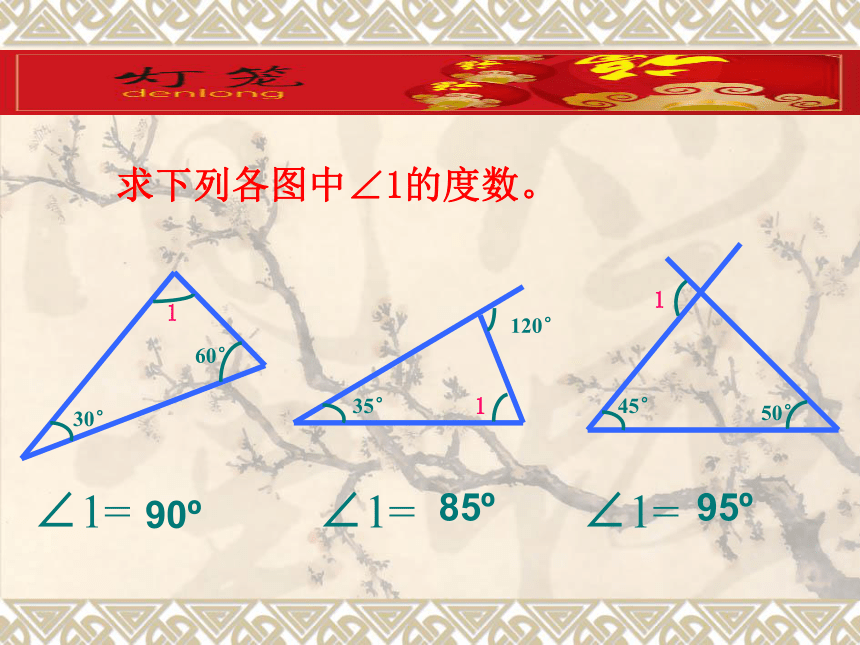
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90
85
95
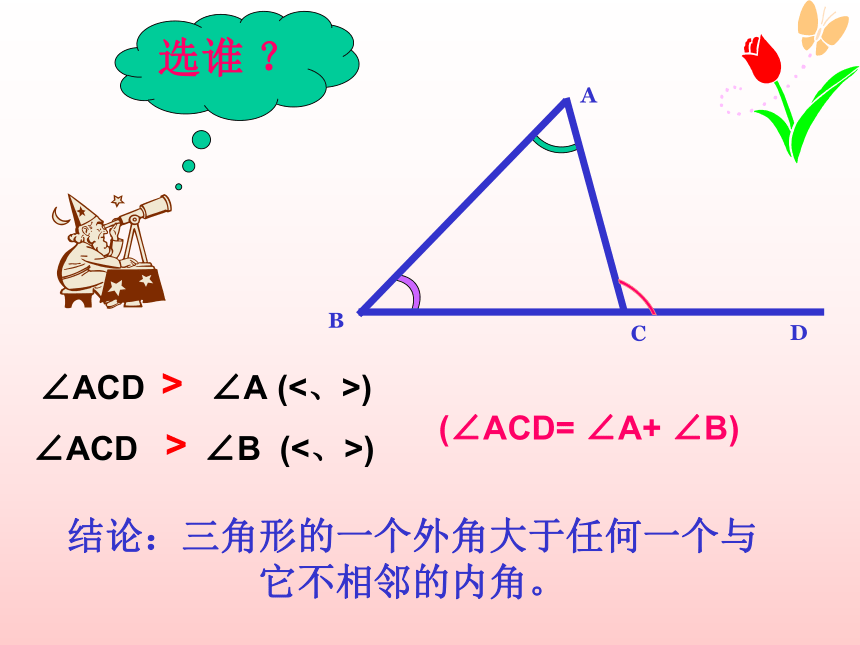
∠ACD ∠B (<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
选谁 ?
(∠ACD= ∠A+ ∠B)
∠ACD ∠A (<、>)
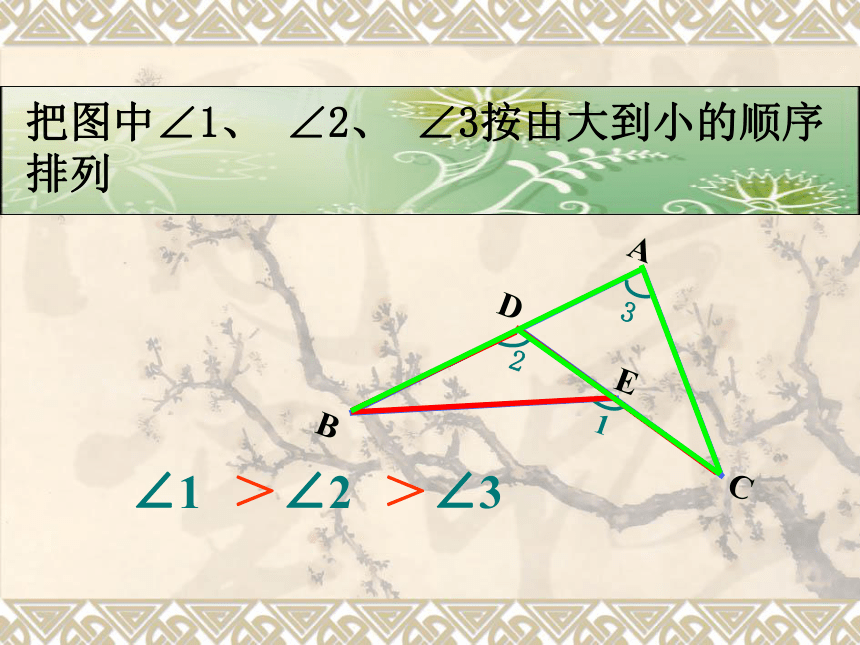
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
画图并思考:
画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳
每一个三角形都有6个外角.
每一个顶点处的外角都有2个,这两个外角是对顶角.
A
B
C
A
B
C
1
2
3
方法1
方法2
三角形的外角和等于360°
∠1+∠2 +∠3 =
从哪些途径探究这个结果
议一议
国旗上的数学
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角
∴∠1=∠B+ ∠E
同理∠2=∠A+∠D
在△CFG中
∠C+∠1+∠2=180
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360°
再见
D
因为∠ACD+ ∠ACB=180°
又因为∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
所以∠ACD =180 ° -∠ACB
所以∠A+ ∠B =180 ° -∠ACB
(邻补角的定义)
(三角形内角和180 ° )
(等量代换)
D
解:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
解:过A作AD平行于BC
∴ ∠3= ∠4
B
C
1
2
3
4
A
∴ ∠2= ∠BAD
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
两直线平行,同位角相等
D
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
民勤二中 马正平
三角形的外角
2、在ABC中,
(1)∠C=90°,∠A=30 ° ,则∠B= ;
(2)∠A=50 ° ,∠B=∠C,则∠B= .
1、三角形三个内角的和等于多少度?
3、在△ABC中,
∠A:∠B:∠C=2:3:4则∠A= ,
∠B= ,∠C= ,
40°
60°
80°
65°
60°
A
B
C
D
三角形的外角:
三角形的一边与另一边的反向延长线组成的角.
A
B
C
D
E
看一看:
算一算:
若∠ A=
55 , ∠ B=60 ,
试求∠ ACB, ∠ACD, ∠CAE
的度数.并说出你的理由.
图中哪些角是三角形的内角,
哪些角是三角形的外角?
⌒
⌒
⌒
⌒
⌒
115°
60°
65°
55°
125°
通过上题的计算,你发现∠ACD, ∠ CAE与三角形的内角之间有怎样的数量关系呢?请你试着用自己的语言说一说.
想一想:
三角形的一个外角等于与它不相邻的两个内角的和。
思考:如何说明∠ACD= ∠B+ ∠ A
D
A
B
C
方法1
方法2
三角形的一个外角等于与它不相邻的两个内角的和
求下列各图中∠1的度数。
30°
60°
1
35°
120°
1
45°
50°
1
∠1=
∠1=
∠1=
90
85
95
∠ACD ∠B (<、>)
结论:三角形的一个外角大于任何一个与它不相邻的内角。
D
A
C
B
>
>
选谁 ?
(∠ACD= ∠A+ ∠B)
∠ACD ∠A (<、>)
把图中∠1、 ∠2、 ∠3按由大到小的顺序排列
B
3
2
1
A
C
D
E
∠1
∠2
∠3
>
>
画图并思考:
画一个△ABC ,你能画出它的所有外角来吗?请动手试一试.同时想一想△ABC的外角共有几个呢?
归纳
每一个三角形都有6个外角.
每一个顶点处的外角都有2个,这两个外角是对顶角.
A
B
C
A
B
C
1
2
3
方法1
方法2
三角形的外角和等于360°
∠1+∠2 +∠3 =
从哪些途径探究这个结果
议一议
国旗上的数学
A
B
C
D
E
求∠A+ ∠B+ ∠C+ ∠D+ ∠E的度数
A
B
C
D
E
1
2
F
G
解:∵∠1是△FBE的外角
∴∠1=∠B+ ∠E
同理∠2=∠A+∠D
在△CFG中
∠C+∠1+∠2=180
∴∠A+ ∠ B+∠C+ ∠ D+∠E= 180
1、三角形外角的两条性质
① 三角形的一个外角等于与它不相邻
的两个内角的和。
②三角形的一个外角大于任何一个与它
不相邻的内角。
2、三角形的外角和是360°
再见
D
因为∠ACD+ ∠ACB=180°
又因为∠A+ ∠B+ ∠ACB=180°
所以, ∠A+ ∠B= ∠ACD
解:
A
B
C
所以∠ACD =180 ° -∠ACB
所以∠A+ ∠B =180 ° -∠ACB
(邻补角的定义)
(三角形内角和180 ° )
(等量代换)
D
解:过C作CE平行于AB
A
B
C
1
2
∴ ∠1= ∠B
(两直线平行,同位角相等)
∠2= ∠A
(两直线平行,内错角相等)
∴∠ACD= ∠1+ ∠2= ∠A+ ∠B
E
解:过A作AD平行于BC
∴ ∠3= ∠4
B
C
1
2
3
4
A
∴ ∠2= ∠BAD
∴ ∠1+ ∠2+ ∠3= ∠1+ ∠BAD+ ∠4=360°
两直线平行,同位角相等
D
A
B
C
1
2
3
∠2+ ∠ABC=180°
∠3+ ∠ACB=180°
三个式子相加得到
∠1+ ∠2+ ∠3+ ∠BAC+ ∠ABC+∠ACB=540°
而∠BAC+ ∠ABC+∠ACB=180°
∠1+ ∠2+ ∠3=360°
∠1+ ∠BAC=180°
解:
