2020-2021学年黑龙江省哈尔滨市南岗区八年级(下)期末数学试卷(五四学制)(Word版 无答案)
文档属性
| 名称 | 2020-2021学年黑龙江省哈尔滨市南岗区八年级(下)期末数学试卷(五四学制)(Word版 无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 162.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-05 16:20:08 | ||
图片预览

文档简介
2020-2021学年黑龙江省哈尔滨市南岗区八年级(下)期末数学试卷(五四学制)
一、选择题(每小题3分,共计30分)
1.下列方程中,是关于x的一元二次方程的是( )
A.x2+2x﹣4=0 B.2x+8=3x﹣4 C.x3﹣x=2 D.
2.下列各组数中能作为直角三角形三边长的是( )
A.1,,2 B.3,4,5 C.4,5,6 D.13,14,15
3.若平行四边形ABCD中,∠A=38°,则∠C的度数为( )
A.38° B.52° C.128° D.142°
4.若正比例函数y=kx(k≠0)的图象经过点(﹣2,3),则k的值为( )
A. B.﹣2 C. D.3
5.如图,一木杆在离地面3m处折断,木杆顶端落在离木杆底端4m处,则木杆折断之前的高度为( )
A.5m B.7m C.8m D.9m
6.下列命题中,是假命题的是( )
A.四个角都相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线互相垂直且相等的四边形是正方形
D.对角线互相平分且垂直的四边形是菱形
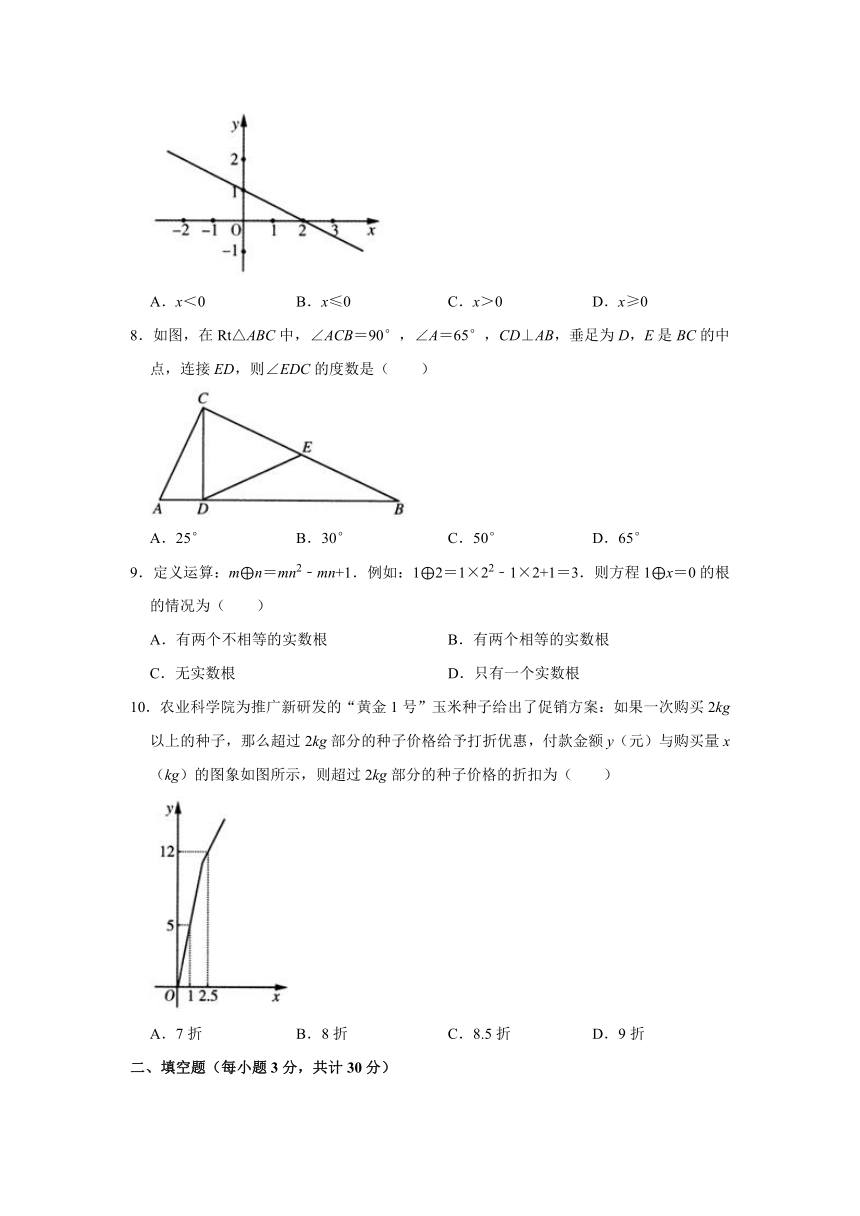
7.直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤1的解集是( )
A.x<0 B.x≤0 C.x>0 D.x≥0
8.如图,在Rt△ABC中,∠ACB=90°,∠A=65°,CD⊥AB,垂足为D,E是BC的中点,连接ED,则∠EDC的度数是( )
A.25° B.30° C.50° D.65°
9.定义运算:m⊕n=mn2﹣mn+1.例如:1⊕2=1×22﹣1×2+1=3.则方程1⊕x=0的根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
10.农业科学院为推广新研发的“黄金1号”玉米种子给出了促销方案:如果一次购买2kg以上的种子,那么超过2kg部分的种子价格给予打折优惠,付款金额y(元)与购买量x(kg)的图象如图所示,则超过2kg部分的种子价格的折扣为( )
A.7折 B.8折 C.8.5折 D.9折
二、填空题(每小题3分,共计30分)
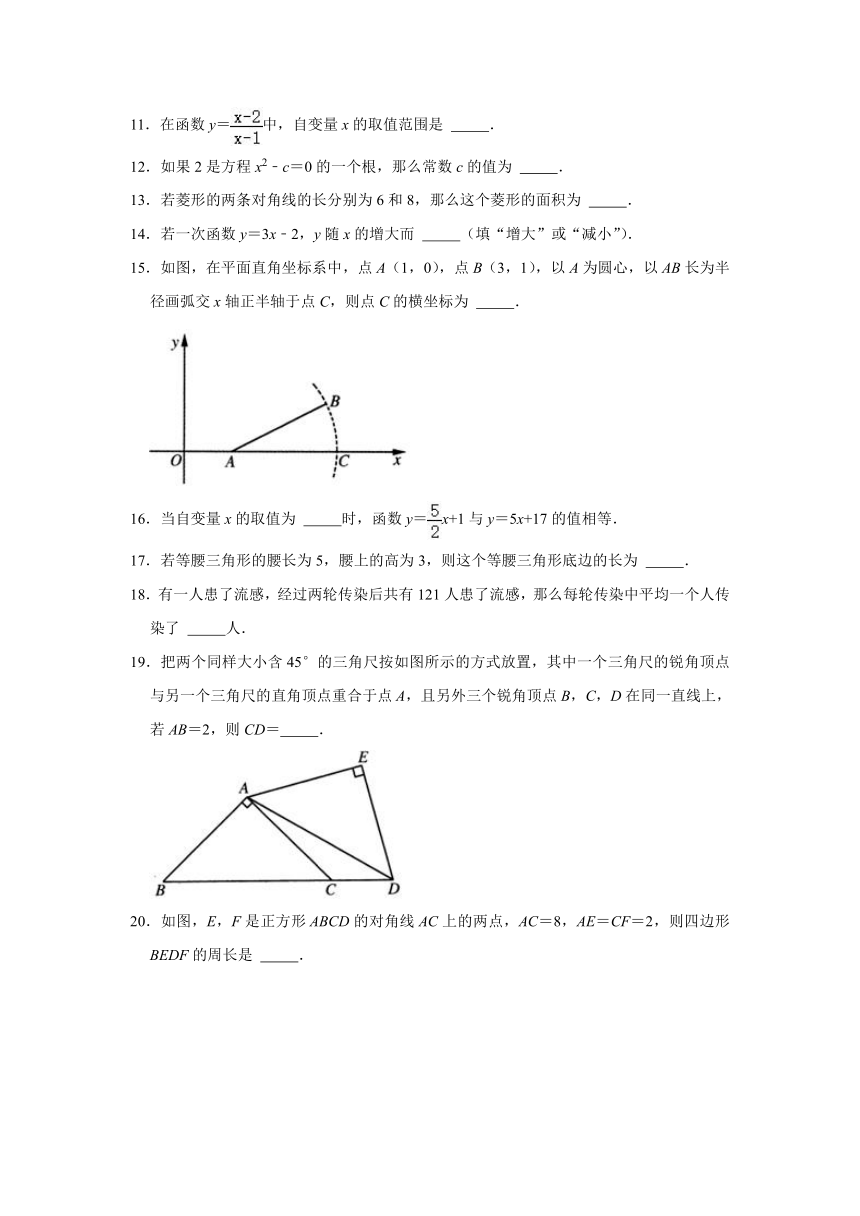
11.在函数y=中,自变量x的取值范围是 .
12.如果2是方程x2﹣c=0的一个根,那么常数c的值为 .
13.若菱形的两条对角线的长分别为6和8,那么这个菱形的面积为 .
14.若一次函数y=3x﹣2,y随x的增大而 (填“增大”或“减小”).
15.如图,在平面直角坐标系中,点A(1,0),点B(3,1),以A为圆心,以AB长为半径画弧交x轴正半轴于点C,则点C的横坐标为 .
16.当自变量x的取值为 时,函数y=x+1与y=5x+17的值相等.
17.若等腰三角形的腰长为5,腰上的高为3,则这个等腰三角形底边的长为 .
18.有一人患了流感,经过两轮传染后共有121人患了流感,那么每轮传染中平均一个人传染了 人.
19.把两个同样大小含45°的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上,若AB=2,则CD= .
20.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.解方程:x(2x﹣4)=5﹣8x.
22.如图,方格纸中每个小正方形的边长均为1,线段AB和线段CD的端点均在小正方形的顶点上.
(1)在方格纸中画以AB为一边的正方形ABEF,点E和点F均在小正方形的顶点上;
(2)在方格纸中画以CD为一边的菱形CDGH,点G和点H均在小正方形的顶点上,菱形CDGH的面积为20,连接FG,并直接写出线段FG的长.
23.某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油量为5L,在整个过程中,油箱里的油量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)填空:机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L;
(2)求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.
24.如图,点A,F,C,D在同一直线上,点B,E分别在直线AD两侧,且AB=DE,∠A=∠D,AF=CD.
(1)求证:四边形BFEC是平行四边形;
(2)若∠ABC=90°,AB=4,BC=3,当AF=时,四边形BFEC是菱形.
25.某商品进价为每件40元,现售价为每件60元,每星期可卖出300件,经市场调查反映,每次涨价1元,每星期可少卖10件.
(1)在一个星期内要想获利6090元的利润,尽量减少库存,该商品应涨价多少元;
(2)在一个星期内能否获利7000元,若能,请求出商品的定价,若不能,请说明理由.
26.已知:在平行四边形ABCD中,点E在AD上,且AE=CD,连接BE.
(1)如图1,求证:∠ABE=∠CBE;
(2)如图2,点F在线段BE上,且BF=BC,连接CE,若∠CED=3∠BEC,求证:AD+CF=BE;
(3)如图3,在(2)的条件下,过点C作CG⊥BE,垂足为点G,若BE=12FG,EF=4,求平行四边形ABCD的面积.
27.已知:在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b交x轴于点A(8,0),交y轴于点B.
(1)如图1,求点B的坐标;
(2)如图2,点P为线段AB上一点,点Q为x轴负半轴上一点,连接BQ,PQ,且PQ=BQ,设点P的横坐标为t,AQ的长为d,求d与t之间的函数解析式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点P作BQ的垂线,分别交x轴,BQ于点C,D,过点O作OE⊥CD于点E,连接QE,若QE平分△PQD的周长,求d的值.
一、选择题(每小题3分,共计30分)
1.下列方程中,是关于x的一元二次方程的是( )
A.x2+2x﹣4=0 B.2x+8=3x﹣4 C.x3﹣x=2 D.
2.下列各组数中能作为直角三角形三边长的是( )
A.1,,2 B.3,4,5 C.4,5,6 D.13,14,15
3.若平行四边形ABCD中,∠A=38°,则∠C的度数为( )
A.38° B.52° C.128° D.142°
4.若正比例函数y=kx(k≠0)的图象经过点(﹣2,3),则k的值为( )
A. B.﹣2 C. D.3
5.如图,一木杆在离地面3m处折断,木杆顶端落在离木杆底端4m处,则木杆折断之前的高度为( )
A.5m B.7m C.8m D.9m
6.下列命题中,是假命题的是( )
A.四个角都相等的四边形是矩形
B.对角线相等的平行四边形是矩形
C.对角线互相垂直且相等的四边形是正方形
D.对角线互相平分且垂直的四边形是菱形
7.直线y=kx+b在平面直角坐标系中的位置如图所示,则不等式kx+b≤1的解集是( )
A.x<0 B.x≤0 C.x>0 D.x≥0
8.如图,在Rt△ABC中,∠ACB=90°,∠A=65°,CD⊥AB,垂足为D,E是BC的中点,连接ED,则∠EDC的度数是( )
A.25° B.30° C.50° D.65°
9.定义运算:m⊕n=mn2﹣mn+1.例如:1⊕2=1×22﹣1×2+1=3.则方程1⊕x=0的根的情况为( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.无实数根 D.只有一个实数根
10.农业科学院为推广新研发的“黄金1号”玉米种子给出了促销方案:如果一次购买2kg以上的种子,那么超过2kg部分的种子价格给予打折优惠,付款金额y(元)与购买量x(kg)的图象如图所示,则超过2kg部分的种子价格的折扣为( )
A.7折 B.8折 C.8.5折 D.9折
二、填空题(每小题3分,共计30分)
11.在函数y=中,自变量x的取值范围是 .
12.如果2是方程x2﹣c=0的一个根,那么常数c的值为 .
13.若菱形的两条对角线的长分别为6和8,那么这个菱形的面积为 .
14.若一次函数y=3x﹣2,y随x的增大而 (填“增大”或“减小”).
15.如图,在平面直角坐标系中,点A(1,0),点B(3,1),以A为圆心,以AB长为半径画弧交x轴正半轴于点C,则点C的横坐标为 .
16.当自变量x的取值为 时,函数y=x+1与y=5x+17的值相等.
17.若等腰三角形的腰长为5,腰上的高为3,则这个等腰三角形底边的长为 .
18.有一人患了流感,经过两轮传染后共有121人患了流感,那么每轮传染中平均一个人传染了 人.
19.把两个同样大小含45°的三角尺按如图所示的方式放置,其中一个三角尺的锐角顶点与另一个三角尺的直角顶点重合于点A,且另外三个锐角顶点B,C,D在同一直线上,若AB=2,则CD= .
20.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是 .
三、解答题(其中21-22题各7分,23-24题各8分,25-27题各10分,共计60分)
21.解方程:x(2x﹣4)=5﹣8x.
22.如图,方格纸中每个小正方形的边长均为1,线段AB和线段CD的端点均在小正方形的顶点上.
(1)在方格纸中画以AB为一边的正方形ABEF,点E和点F均在小正方形的顶点上;
(2)在方格纸中画以CD为一边的菱形CDGH,点G和点H均在小正方形的顶点上,菱形CDGH的面积为20,连接FG,并直接写出线段FG的长.
23.某种机器工作前先将空油箱加满,然后停止加油立即开始工作.当停止工作时,油箱中油量为5L,在整个过程中,油箱里的油量y(单位:L)与时间x(单位:min)之间的关系如图所示.
(1)填空:机器每分钟加油量为L,机器工作的过程中每分钟耗油量为L;
(2)求机器工作时y关于x的函数解析式,并写出自变量x的取值范围.
24.如图,点A,F,C,D在同一直线上,点B,E分别在直线AD两侧,且AB=DE,∠A=∠D,AF=CD.
(1)求证:四边形BFEC是平行四边形;
(2)若∠ABC=90°,AB=4,BC=3,当AF=时,四边形BFEC是菱形.
25.某商品进价为每件40元,现售价为每件60元,每星期可卖出300件,经市场调查反映,每次涨价1元,每星期可少卖10件.
(1)在一个星期内要想获利6090元的利润,尽量减少库存,该商品应涨价多少元;
(2)在一个星期内能否获利7000元,若能,请求出商品的定价,若不能,请说明理由.
26.已知:在平行四边形ABCD中,点E在AD上,且AE=CD,连接BE.
(1)如图1,求证:∠ABE=∠CBE;
(2)如图2,点F在线段BE上,且BF=BC,连接CE,若∠CED=3∠BEC,求证:AD+CF=BE;
(3)如图3,在(2)的条件下,过点C作CG⊥BE,垂足为点G,若BE=12FG,EF=4,求平行四边形ABCD的面积.
27.已知:在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b交x轴于点A(8,0),交y轴于点B.
(1)如图1,求点B的坐标;
(2)如图2,点P为线段AB上一点,点Q为x轴负半轴上一点,连接BQ,PQ,且PQ=BQ,设点P的横坐标为t,AQ的长为d,求d与t之间的函数解析式(不要求写出自变量t的取值范围);
(3)如图3,在(2)的条件下,过点P作BQ的垂线,分别交x轴,BQ于点C,D,过点O作OE⊥CD于点E,连接QE,若QE平分△PQD的周长,求d的值.
同课章节目录
