8.5 三视图1
图片预览








文档简介
(共53张PPT)
8.5三视图
旧县中学: 初三
新华社8月25日电: 2011年8月18日-25日历时8天的“和平使命-2011”中俄联合军事演习25日下午结束,曹刚川和伊万诺夫在演兵场检阅了两军陆海空军参演部队。 ... 伊万诺夫在俄中军事演习结束后表示,今后两国还将会举行新的联合军事演习,俄中携手团结将成为亚太地区和平与稳定的重要保障。
新闻连接
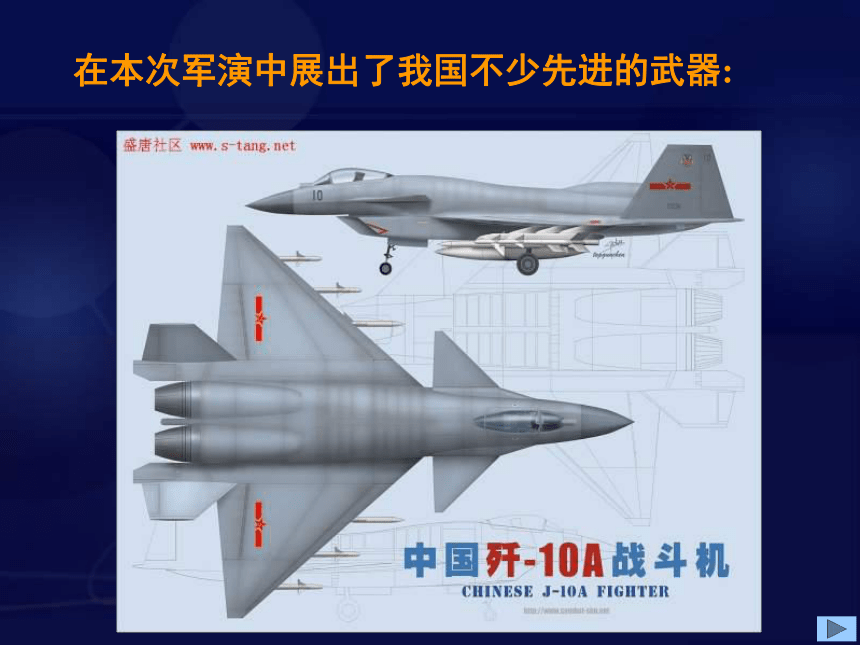
在本次军演中展出了我国不少先进的武器:
看一看
看一看
看一看
看一看
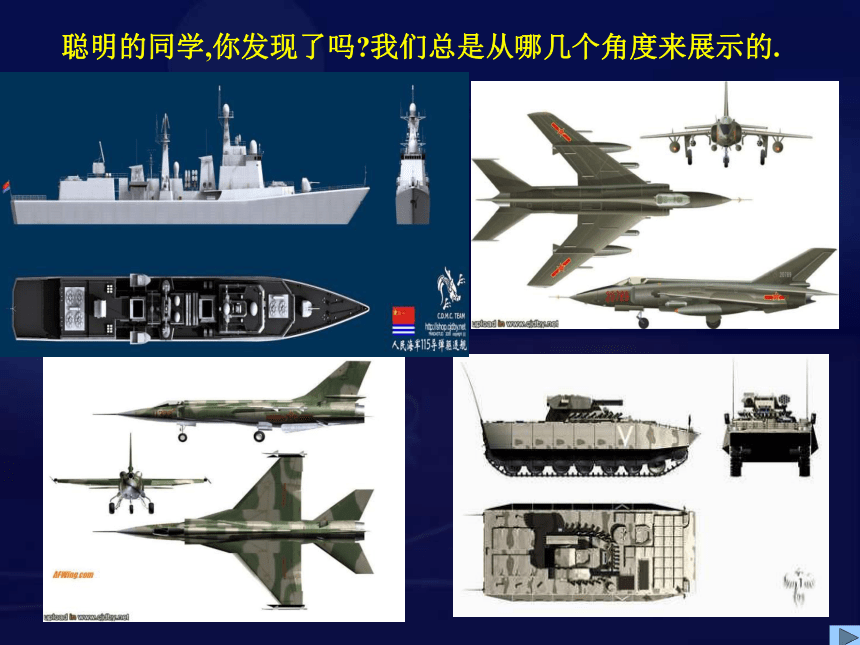
聪明的同学,你发现了吗 我们总是从哪几个角度来展示的.
从正面看
从侧面看
从上面看
飞机
模型
在生活中我们应从不同角度,多方面地去看待一件事物,分析一件事情。
数学中我们只从三个不同方向看同一物体,所以,每一个物体都有三视图。
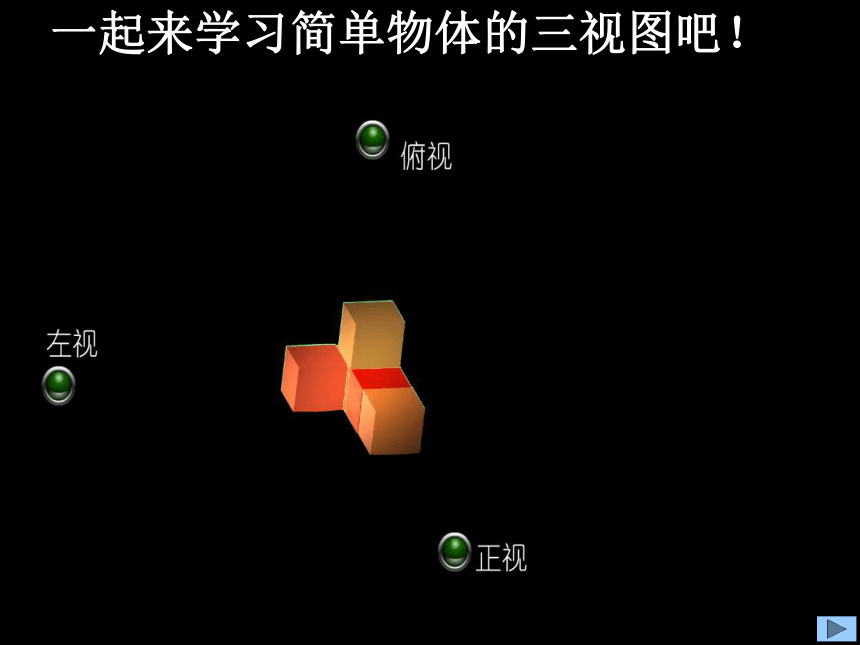
一起来学习简单物体的三视图吧!
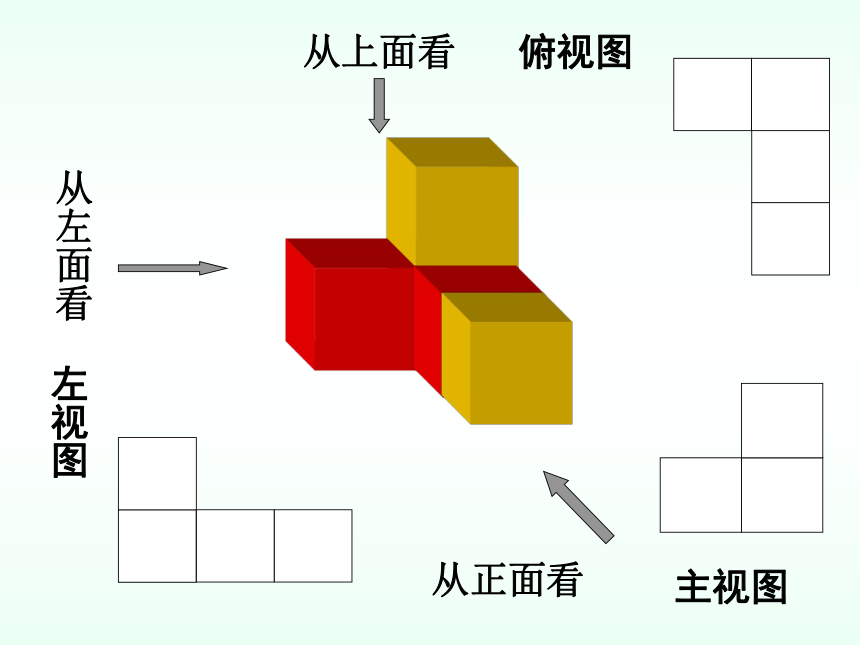
从左面看
从上面看
从正面看
主视图
俯视图
左视图
从上面看
从左面看
从正面看
主视图
左视图
俯视图
你能画出正方体和的三视图吗?
主 视 图
左 视 图
俯 视 图
想一想,再动手画一画:
高平齐
高平齐:主视图和左视图共同反映了物体上下方向的尺寸.
主 视 图
左 视 图
俯 视 图
长对正
长对正:主视图和俯视图共同反映了物体左右方向的尺寸.
你会画圆柱的三视图吗?试一试吧!
试一试
主 视 图
左 视 图
俯 视 图
宽相等
宽相等:俯视图和左视图共同反映了物体前后方向的尺寸.
画出如图所示四棱锥的三视图。
挑战自我
正 视 图
左 视 图
俯 视 图
俯 视 图
左 视 图
主 视 图
宽相等
高平齐
长对正
理一理:
1、从正面看到的图形叫做主视图,从上面看到的图形叫做俯视图,从左面看到的图形叫做左视图。
2、画三视图必须遵循的法则:“长对齐,高平齐,宽相等”
3、基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆。
(4)棱锥的三视图中有两个是三角形,另一个是正方形。
(5)球体的三视图都是圆形。
我相信你一定能画出这个复杂几何体的三视图!
1、画出下列立体图形的三视图。
2、指出左面三个平面图形是右面这个物体的三视图中
的哪个视图。
(
(
(
正视图)
俯视图)
左视图)
练一练
正视图
俯视图
左视图
练一练
正视图
俯视图
侧视图
练一练
你能说出下面这个几何体的三视图吗?
请画出如图所示的三视图
(A)
(1)
(2)
平面图形
学到了什么?
平面图
看到了什么画什么
从正
面看
从左
面看
从上
面看
实物图
立体图
平面图
平面图
三视图
主视图
左视图
俯视图
想一想?
A
C
B
D
下面三视图是表示哪个几何体?
侧视图
正视图
俯视图
A
B
思考:下图中的三视图表示哪个几何体?
俯视图
左视图
正视图
A
B
C
( )
( )
( )
B
C
B
俯视图
左视图
正视图
A
B
C
( )
( )
( )
A
A
B
考考你
【探究】
1、如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
探究
你能摆出这个几何体吗?
试画出这个几何体的正视图与侧视图。
正视图:
侧视图:
1
1
2
2
1
1
2
2
正视图:
侧视图:
思考方法
先根据俯视图确定正视图有 列,
3
再根据数字确定每列的方块有 个,
不用摆出这个几何体,你能画出这个几何体的正视图与左视图吗?
正视图有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
侧视图有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
【反思】
2、你能由三视图得到该几何体吗?
3、你会由“给出数字的俯视图”画出几何体的正视图、侧视图吗?
1、你能画出一个几何体的三视图吗?
动手设计
请画出下面立体图形的三视图。
俯视方向
注意:根据“长对正,高平齐,宽相等” 画
三视图必须遵循的法则作图。
画好后,请你自己参照课本65页的图3—21给自己画的
图打分,并把画得不够好的地方修改过来,加油!
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。请你举一些例子加以说明。
提示:例如正方体的主视图是一个张方形,但主视图是正方形的几何体就有很多,如四棱柱,长方体,圆柱等。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
想一想:
题西林壁 苏轼
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
诗中说明了怎样的一个数学道理?
横看成岭侧成峰,
远近高低各不同.
不识庐山真面目,
只缘身在此山中.
题西林壁
苏轼
2、会画简单立体图形的三视图.
1、三视图的概念;
谈谈收获
祝同学们2012中考成功
8.5三视图
旧县中学: 初三
新华社8月25日电: 2011年8月18日-25日历时8天的“和平使命-2011”中俄联合军事演习25日下午结束,曹刚川和伊万诺夫在演兵场检阅了两军陆海空军参演部队。 ... 伊万诺夫在俄中军事演习结束后表示,今后两国还将会举行新的联合军事演习,俄中携手团结将成为亚太地区和平与稳定的重要保障。
新闻连接
在本次军演中展出了我国不少先进的武器:
看一看
看一看
看一看
看一看
聪明的同学,你发现了吗 我们总是从哪几个角度来展示的.
从正面看
从侧面看
从上面看
飞机
模型
在生活中我们应从不同角度,多方面地去看待一件事物,分析一件事情。
数学中我们只从三个不同方向看同一物体,所以,每一个物体都有三视图。
一起来学习简单物体的三视图吧!
从左面看
从上面看
从正面看
主视图
俯视图
左视图
从上面看
从左面看
从正面看
主视图
左视图
俯视图
你能画出正方体和的三视图吗?
主 视 图
左 视 图
俯 视 图
想一想,再动手画一画:
高平齐
高平齐:主视图和左视图共同反映了物体上下方向的尺寸.
主 视 图
左 视 图
俯 视 图
长对正
长对正:主视图和俯视图共同反映了物体左右方向的尺寸.
你会画圆柱的三视图吗?试一试吧!
试一试
主 视 图
左 视 图
俯 视 图
宽相等
宽相等:俯视图和左视图共同反映了物体前后方向的尺寸.
画出如图所示四棱锥的三视图。
挑战自我
正 视 图
左 视 图
俯 视 图
俯 视 图
左 视 图
主 视 图
宽相等
高平齐
长对正
理一理:
1、从正面看到的图形叫做主视图,从上面看到的图形叫做俯视图,从左面看到的图形叫做左视图。
2、画三视图必须遵循的法则:“长对齐,高平齐,宽相等”
3、基本几何体的三视图:
(1)正方体的三视图都是正方形。
(2)圆柱的三视图中有两个是长方形,另一个是圆。
(3)圆锥的三视图中有两个是三角形,另一个是圆。
(4)棱锥的三视图中有两个是三角形,另一个是正方形。
(5)球体的三视图都是圆形。
我相信你一定能画出这个复杂几何体的三视图!
1、画出下列立体图形的三视图。
2、指出左面三个平面图形是右面这个物体的三视图中
的哪个视图。
(
(
(
正视图)
俯视图)
左视图)
练一练
正视图
俯视图
左视图
练一练
正视图
俯视图
侧视图
练一练
你能说出下面这个几何体的三视图吗?
请画出如图所示的三视图
(A)
(1)
(2)
平面图形
学到了什么?
平面图
看到了什么画什么
从正
面看
从左
面看
从上
面看
实物图
立体图
平面图
平面图
三视图
主视图
左视图
俯视图
想一想?
A
C
B
D
下面三视图是表示哪个几何体?
侧视图
正视图
俯视图
A
B
思考:下图中的三视图表示哪个几何体?
俯视图
左视图
正视图
A
B
C
( )
( )
( )
B
C
B
俯视图
左视图
正视图
A
B
C
( )
( )
( )
A
A
B
考考你
【探究】
1、如右图是由几个小立方体所搭几何体的俯视图,小正方形中的数字表示在该位置小正方体的个数。
探究
你能摆出这个几何体吗?
试画出这个几何体的正视图与侧视图。
正视图:
侧视图:
1
1
2
2
1
1
2
2
正视图:
侧视图:
思考方法
先根据俯视图确定正视图有 列,
3
再根据数字确定每列的方块有 个,
不用摆出这个几何体,你能画出这个几何体的正视图与左视图吗?
正视图有 列,
第一列的方块有 个,
1
第二列的方块有 个,
2
第三列的方块有 个,
1
侧视图有 列,
2
第一列的方块有 个,
2
第二列的方块有 个,
2
【反思】
2、你能由三视图得到该几何体吗?
3、你会由“给出数字的俯视图”画出几何体的正视图、侧视图吗?
1、你能画出一个几何体的三视图吗?
动手设计
请画出下面立体图形的三视图。
俯视方向
注意:根据“长对正,高平齐,宽相等” 画
三视图必须遵循的法则作图。
画好后,请你自己参照课本65页的图3—21给自己画的
图打分,并把画得不够好的地方修改过来,加油!
辨一辨,说一说:
1、一个几何体的视图是唯一的,但从视图反过来考虑几何体时,它有多种可能性。请你举一些例子加以说明。
提示:例如正方体的主视图是一个张方形,但主视图是正方形的几何体就有很多,如四棱柱,长方体,圆柱等。
横看成岭侧成峰,远近高低各不同。
不识庐山真面目,只缘身在此山中。
——苏轼
想一想:
题西林壁 苏轼
横看成岭侧成峰,
远近高低各不同。
不识庐山真面目,
只缘身在此山中。
诗中说明了怎样的一个数学道理?
横看成岭侧成峰,
远近高低各不同.
不识庐山真面目,
只缘身在此山中.
题西林壁
苏轼
2、会画简单立体图形的三视图.
1、三视图的概念;
谈谈收获
祝同学们2012中考成功
