11.4.2平面与平面垂直(第2课时)教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册
文档属性
| 名称 | 11.4.2平面与平面垂直(第2课时)教案-2020-2021学年高一下学期数学人教B版(2019)必修第四册 | 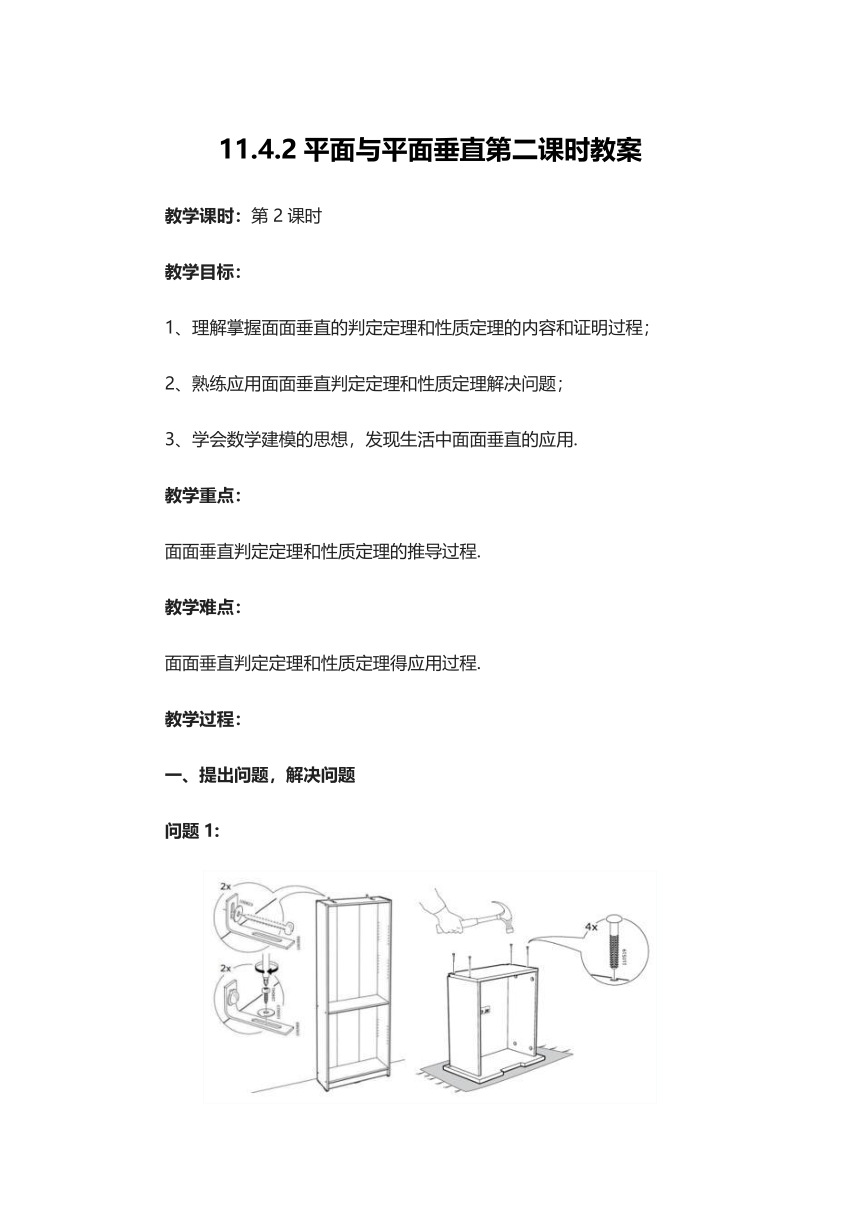 | |
| 格式 | docx | ||
| 文件大小 | 125.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 09:21:31 | ||
图片预览


文档简介
11.4.2平面与平面垂直第二课时教案
教学课时:第2课时
教学目标:
1、理解掌握面面垂直的判定定理和性质定理的内容和证明过程;
2、熟练应用面面垂直判定定理和性质定理解决问题;
3、学会数学建模的思想,发现生活中面面垂直的应用.
教学重点:
面面垂直判定定理和性质定理的推导过程.
教学难点:
面面垂直判定定理和性质定理得应用过程.
教学过程:
一、提出问题,解决问题
问题1:
两个图都是家居柜体的组装说明书.
第一个图,为了使柜体上表面和墙垂直,用了一个三角铁;
第二个图,为了使柜体上表面和侧面垂直,用了一个垂直于上表面的钉子并让侧面板过这个钉子.
那两种方法是否能让目标面相互垂直呢?他们其中能提炼出怎样的数学理论呢?大家可以以小组为单位进行讨论.
【学生活动1】
引导学生通过对实例的观察找到两者的共同之处就是都能让目标面相互垂直,再引导学生找到他们不同之处就是一个是通过二面角是直角的原理,一个是过面的垂线的面与另一个面垂直.
【设计意图】
让学生学会自己找到事物的共性和区别。并且对本节要学习的面面垂直有一个直观的感觉和认识.
二、数学建模,得出定理
问题2:验证第二个方案是不是可行那这个过程其实就是数学建模的过程:数学建模就是根据实际问题来建立数学模型,对数学模型来进行求解,然后根据结果去解决实际问题。上面的问题数学建模应该是:
如果.
【学生活动2】
证明:因为.
过O在平面,所以
因此我们得到:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直,我们称之为平面与平面垂直的判定定理.
【设计意图】
1、通过数学建模的思维让学生学会从实际问题中构建数学模型,解决构建的数学模型,得到模型结论再反作用于实际问题的思维过程;
2、让学生掌握在找不到二面角的平面角的情况下去证明两平面垂直的方法.
问题3:在受到前面学习过的线线垂直和线面垂直互推关系的启发,我们可以尝试去寻找在已知面面垂直的前提下能否推出其他性质呢?
这就是面面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。用符号表示为:如果,.
【学生活动3】
同学们以小组为单位依照判定定理的推到逻辑尝试得出性质定理得推导过程.
如图
证明:,过O在平面内作与m垂直的直线OB,AOB为二面角A-m-B的平面角,因为,所以,.
【设计意图】
通过对第一个定理得证明过程,让学生学会分析性质定理得证明过程并掌握几何语言的叙述方式.
三、定理应用,知识升华
问题4:如图所示,已知,在,且AC,BD分别在内,它们都垂直于交线AB,并且AC=1.BD=2.
(1)求CD长;(2)求证:平面CBD平面ABC.
解:(1)连接BC,因为;
又因为,因此三角形CBD是直角三角形.
在中,
(2)由(1)知BDBC,BDAB,所以BD平面ABC,
又因为.
【设计意图】
让学生把这节课学习的判定定理进行实际操作,以达到巩固、掌握、熟悉的目的.
四、本节小结,课后作业
通过本堂课的学习我们了解了证明两个平面垂直,除了找到二面角的平面角并证明是直角外,我们还学会了平面与平面垂直的判定定理,并且我们在两平面已知垂直的前提下还能得到线面垂直的性质,这些性质和定理无论在做题中还是在实际生活中都是有着广泛的应用,希望同学们在了解、掌握本节课内容的前提下能自行完成书后练习题,以及发现身边与平面垂直有关系的实际案例.
教学课时:第2课时
教学目标:
1、理解掌握面面垂直的判定定理和性质定理的内容和证明过程;
2、熟练应用面面垂直判定定理和性质定理解决问题;
3、学会数学建模的思想,发现生活中面面垂直的应用.
教学重点:
面面垂直判定定理和性质定理的推导过程.
教学难点:
面面垂直判定定理和性质定理得应用过程.
教学过程:
一、提出问题,解决问题
问题1:
两个图都是家居柜体的组装说明书.
第一个图,为了使柜体上表面和墙垂直,用了一个三角铁;
第二个图,为了使柜体上表面和侧面垂直,用了一个垂直于上表面的钉子并让侧面板过这个钉子.
那两种方法是否能让目标面相互垂直呢?他们其中能提炼出怎样的数学理论呢?大家可以以小组为单位进行讨论.
【学生活动1】
引导学生通过对实例的观察找到两者的共同之处就是都能让目标面相互垂直,再引导学生找到他们不同之处就是一个是通过二面角是直角的原理,一个是过面的垂线的面与另一个面垂直.
【设计意图】
让学生学会自己找到事物的共性和区别。并且对本节要学习的面面垂直有一个直观的感觉和认识.
二、数学建模,得出定理
问题2:验证第二个方案是不是可行那这个过程其实就是数学建模的过程:数学建模就是根据实际问题来建立数学模型,对数学模型来进行求解,然后根据结果去解决实际问题。上面的问题数学建模应该是:
如果.
【学生活动2】
证明:因为.
过O在平面,所以
因此我们得到:如果一个平面经过另一个平面的一条垂线,则这两个平面互相垂直,我们称之为平面与平面垂直的判定定理.
【设计意图】
1、通过数学建模的思维让学生学会从实际问题中构建数学模型,解决构建的数学模型,得到模型结论再反作用于实际问题的思维过程;
2、让学生掌握在找不到二面角的平面角的情况下去证明两平面垂直的方法.
问题3:在受到前面学习过的线线垂直和线面垂直互推关系的启发,我们可以尝试去寻找在已知面面垂直的前提下能否推出其他性质呢?
这就是面面垂直的性质定理:如果两个平面互相垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面。用符号表示为:如果,.
【学生活动3】
同学们以小组为单位依照判定定理的推到逻辑尝试得出性质定理得推导过程.
如图
证明:,过O在平面内作与m垂直的直线OB,AOB为二面角A-m-B的平面角,因为,所以,.
【设计意图】
通过对第一个定理得证明过程,让学生学会分析性质定理得证明过程并掌握几何语言的叙述方式.
三、定理应用,知识升华
问题4:如图所示,已知,在,且AC,BD分别在内,它们都垂直于交线AB,并且AC=1.BD=2.
(1)求CD长;(2)求证:平面CBD平面ABC.
解:(1)连接BC,因为;
又因为,因此三角形CBD是直角三角形.
在中,
(2)由(1)知BDBC,BDAB,所以BD平面ABC,
又因为.
【设计意图】
让学生把这节课学习的判定定理进行实际操作,以达到巩固、掌握、熟悉的目的.
四、本节小结,课后作业
通过本堂课的学习我们了解了证明两个平面垂直,除了找到二面角的平面角并证明是直角外,我们还学会了平面与平面垂直的判定定理,并且我们在两平面已知垂直的前提下还能得到线面垂直的性质,这些性质和定理无论在做题中还是在实际生活中都是有着广泛的应用,希望同学们在了解、掌握本节课内容的前提下能自行完成书后练习题,以及发现身边与平面垂直有关系的实际案例.
