三角形的外角和学案
图片预览
文档简介
三角形的外角和
第一课时(课本 62页—63页)
学习目的
1.使学生在操作活动中,探索三角形的外角的两条性质以及三角形的外角和。
2.利用平行线性质来证明三角形的外角的第一个性质以及三角形 的外角和。
3.使学生能熟练地利用三角形内角和,外角和以及外角的两条性质进行有关计算。
重点:三角形内角和定理
难点:三角形内角和定理的推理的过程
一、新知准备与自学:(学生自学教材并完成填空后互评)时间:5分钟
如图1中∠CBD是三角形的一个外角,内角 与它相邻,内角 、 与它不相邻。
二、探究合作、展示 :(学生独立思考后小组交流师根据情况点拨)时间:15-20分钟
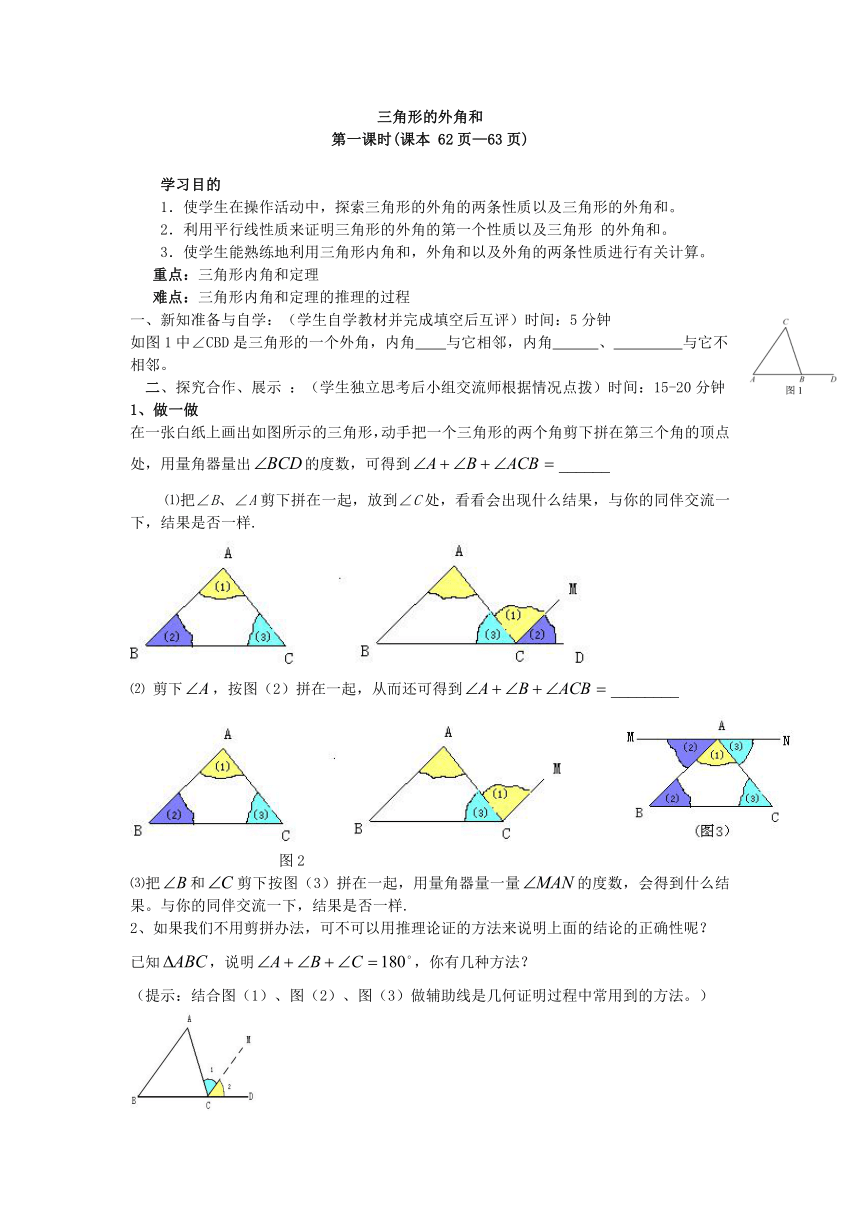
1、做一做
在一张白纸上画出如图所示的三角形,动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到
⑴把∠B、∠A剪下拼在一起,放到∠C处,看看会出现什么结果,与你的同伴交流一下,结果是否一样.
⑵ 剪下,按图(2)拼在一起,从而还可得到
图2
⑶把和剪下按图(3)拼在一起,用量角器量一量的度数,会得到什么结果。与你的同伴交流一下,结果是否一样.
2、如果我们不用剪拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知,说明,你有几种方法?
(提示:结合图(1)、图(2)、图(3)做辅助线是几何证明过程中常用到的方法。)
3、思考:由图1的实践发现:∠A+∠B= ∠ 由此还可得ACD A
归纳:由以上证明和思考 得:
三角形的内角和是
2、由此可知:三角形外角有两条性质:
(1)三角形的一个外角等于 。
(2)三角形的一个外角大于 。
三 、 知识巩固应用。(学生独立完成后小组互评教师根据情况点拨)15-20分钟
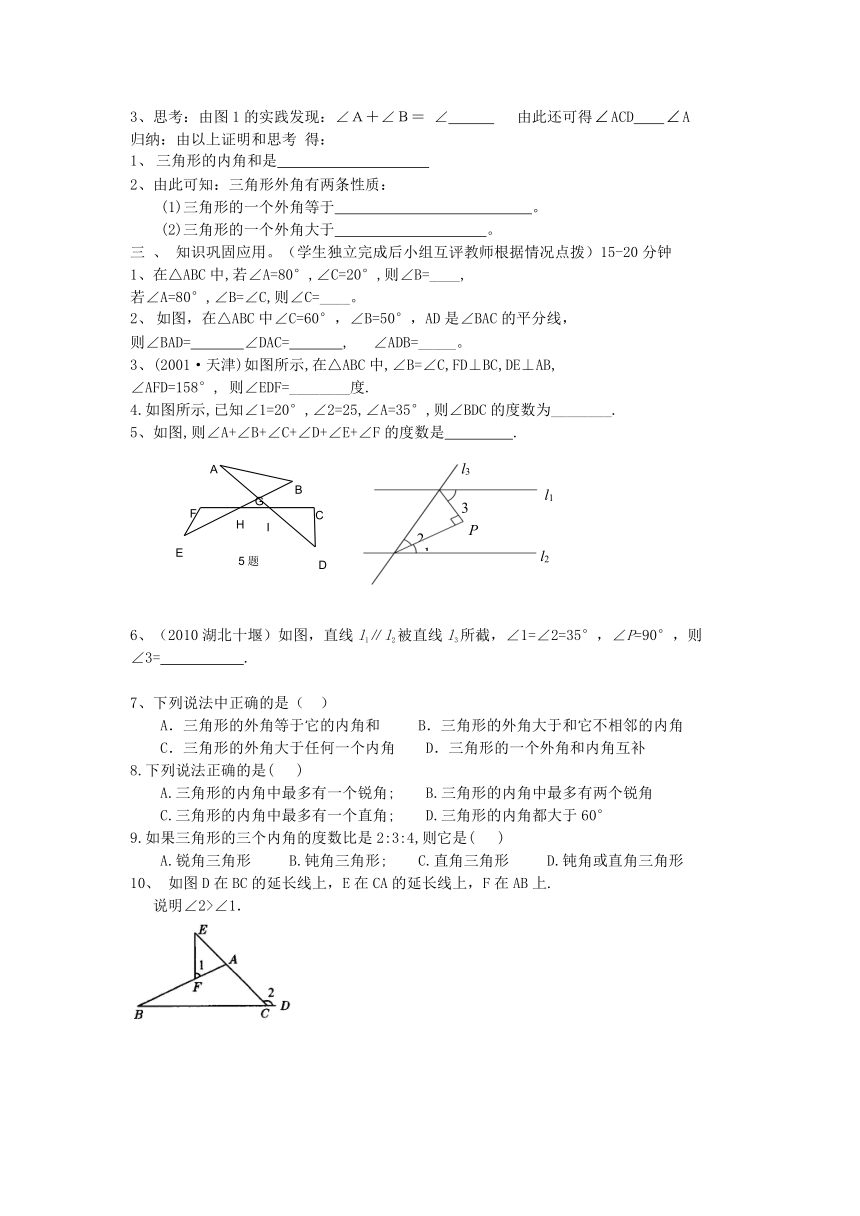
1、在△ABC中,若∠A=80°,∠C=20°,则∠B=____,
若∠A=80°,∠B=∠C,则∠C=____。
如图,在△ABC中∠C=60°,∠B=50°,AD是∠BAC的平分线,
则∠BAD= ∠DAC= , ∠ADB=_____。
3、(2001·天津)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,
∠AFD=158°, 则∠EDF=________度.
4.如图所示,已知∠1=20°,∠2=25,∠A=35°,则∠BDC的度数为________.
5、如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
6、(2010湖北十堰)如图,直线l1∥l2被直线l3所截,∠1=∠2=35°,∠P=90°,则
∠3= .
7、下列说法中正确的是( )
A.三角形的外角等于它的内角和 B.三角形的外角大于和它不相邻的内角
C.三角形的外角大于任何一个内角 D.三角形的一个外角和内角互补
8.下列说法正确的是( )
A.三角形的内角中最多有一个锐角; B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角; D.三角形的内角都大于60°
9.如果三角形的三个内角的度数比是2:3:4,则它是( )毛
A.锐角三角形 B.钝角三角形; C.直角三角形 D.钝角或直角三角形
10、 如图D在BC的延长线上,E在CA的延长线上,F在AB上.
说明∠2>∠1.
三角形的外角和
第二课时 (课本 63页—64页)
学习目的
1、使学生在操作活动中,探索三角形的外角的两条性质和外角和定理。
2、能熟练灵活地利用三角形内角和,外角和以及外角的两条性质进行有关计算。
重点:掌握三角形外角的性质以及其外角的和。
难点:在三角形外角的性质证明的过程中,涉及到添加辅助线来沟通证明思路的方法。
一、新知准备与自学:(学生自学教材并完成填空后互评)时间:5-10分钟
1.如图示填空:
(1)
(2),
(3)
2、想一想, △ABC的外角共有几个呢
二、探究合作、展示 :(学生独立思考后小组交流师根据情况点拨)时间:15-20分钟
1、如图示:思考∠1+∠2 +∠3 =
∵∠1+______________=180°,
∠2+_______________=180°,
∠3+_______________=180°.
三式相加可以得到
∴∠1+∠2+∠3+______+______+______=_______,(1)
又∵ ∠ACB+∠BAC+∠ABC=180°, (2)
∴∠1+∠2+∠3= °
结论:三角形的外角和是
例1、如图9.1.11,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
解 (1)∵∠ADC是△ABD的外角(已知),
∴∠ADC=∠B+∠ =80°
又 ∠B=∠BAD(已知),
∴ ∠ =80°×=40°(等量代换).
(2)在△ABC中,∵∠B+∠ +∠C=180°(三角形的内角和等于180°),
∴ ∠C=180°-∠ -∠ (等式的性质)
=180°-40°-70°=70°
例2、如图所示,在△ABC中,∠A=70°,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.
例3、如图,△ABC中,∠A=500,∠ABC的平分线与∠C的外角∠ACE平分线交于D,
求∠D的度数。
三 、 知识巩固应用。(学生独立完成后小组互评教师根据情况点拨)10-15分钟
1.三角形的三个外角中,最多有_______个锐角.
2.已知等腰三角形的一个外角为150°,则它的底角为_____.
3.如图1所示,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,
则∠BOC=_______,∠D=_____,∠E=________.
4.如图2所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.
5、如图4,则∠A+∠B+∠C+∠D+∠E的度数为 .
6.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90° B.110° C.100° D.120°
7.如图3所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°
(1) (2) (3) (4)
8、如右图,AC∥DE,BD平分∠ABC交AC于F,∠ABC=70°,∠E=50°,求∠D,∠A的度数.
9、 如图所示,在△ABC中,∠A=α,△ABC的内角平分线或外角平分线交于点P, 且∠P=β,试探求下列各图中α与β的关系,并选择一个加以说明.
I
H
G
E
F
D
B
C
A
5题
l1
l2
l3
3
1
2
P
第一课时(课本 62页—63页)
学习目的
1.使学生在操作活动中,探索三角形的外角的两条性质以及三角形的外角和。
2.利用平行线性质来证明三角形的外角的第一个性质以及三角形 的外角和。
3.使学生能熟练地利用三角形内角和,外角和以及外角的两条性质进行有关计算。
重点:三角形内角和定理
难点:三角形内角和定理的推理的过程
一、新知准备与自学:(学生自学教材并完成填空后互评)时间:5分钟
如图1中∠CBD是三角形的一个外角,内角 与它相邻,内角 、 与它不相邻。
二、探究合作、展示 :(学生独立思考后小组交流师根据情况点拨)时间:15-20分钟
1、做一做
在一张白纸上画出如图所示的三角形,动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到
⑴把∠B、∠A剪下拼在一起,放到∠C处,看看会出现什么结果,与你的同伴交流一下,结果是否一样.
⑵ 剪下,按图(2)拼在一起,从而还可得到
图2
⑶把和剪下按图(3)拼在一起,用量角器量一量的度数,会得到什么结果。与你的同伴交流一下,结果是否一样.
2、如果我们不用剪拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知,说明,你有几种方法?
(提示:结合图(1)、图(2)、图(3)做辅助线是几何证明过程中常用到的方法。)
3、思考:由图1的实践发现:∠A+∠B= ∠ 由此还可得ACD A
归纳:由以上证明和思考 得:
三角形的内角和是
2、由此可知:三角形外角有两条性质:
(1)三角形的一个外角等于 。
(2)三角形的一个外角大于 。
三 、 知识巩固应用。(学生独立完成后小组互评教师根据情况点拨)15-20分钟
1、在△ABC中,若∠A=80°,∠C=20°,则∠B=____,
若∠A=80°,∠B=∠C,则∠C=____。
如图,在△ABC中∠C=60°,∠B=50°,AD是∠BAC的平分线,
则∠BAD= ∠DAC= , ∠ADB=_____。
3、(2001·天津)如图所示,在△ABC中,∠B=∠C,FD⊥BC,DE⊥AB,
∠AFD=158°, 则∠EDF=________度.
4.如图所示,已知∠1=20°,∠2=25,∠A=35°,则∠BDC的度数为________.
5、如图,则∠A+∠B+∠C+∠D+∠E+∠F的度数是 .
6、(2010湖北十堰)如图,直线l1∥l2被直线l3所截,∠1=∠2=35°,∠P=90°,则
∠3= .
7、下列说法中正确的是( )
A.三角形的外角等于它的内角和 B.三角形的外角大于和它不相邻的内角
C.三角形的外角大于任何一个内角 D.三角形的一个外角和内角互补
8.下列说法正确的是( )
A.三角形的内角中最多有一个锐角; B.三角形的内角中最多有两个锐角
C.三角形的内角中最多有一个直角; D.三角形的内角都大于60°
9.如果三角形的三个内角的度数比是2:3:4,则它是( )毛
A.锐角三角形 B.钝角三角形; C.直角三角形 D.钝角或直角三角形
10、 如图D在BC的延长线上,E在CA的延长线上,F在AB上.
说明∠2>∠1.
三角形的外角和
第二课时 (课本 63页—64页)
学习目的
1、使学生在操作活动中,探索三角形的外角的两条性质和外角和定理。
2、能熟练灵活地利用三角形内角和,外角和以及外角的两条性质进行有关计算。
重点:掌握三角形外角的性质以及其外角的和。
难点:在三角形外角的性质证明的过程中,涉及到添加辅助线来沟通证明思路的方法。
一、新知准备与自学:(学生自学教材并完成填空后互评)时间:5-10分钟
1.如图示填空:
(1)
(2),
(3)
2、想一想, △ABC的外角共有几个呢
二、探究合作、展示 :(学生独立思考后小组交流师根据情况点拨)时间:15-20分钟
1、如图示:思考∠1+∠2 +∠3 =
∵∠1+______________=180°,
∠2+_______________=180°,
∠3+_______________=180°.
三式相加可以得到
∴∠1+∠2+∠3+______+______+______=_______,(1)
又∵ ∠ACB+∠BAC+∠ABC=180°, (2)
∴∠1+∠2+∠3= °
结论:三角形的外角和是
例1、如图9.1.11,D是△ABC的BC边上一点,∠B=∠BAD,∠ADC=80°,∠BAC=70°.求:
(1)∠B的度数;
(2)∠C的度数.
解 (1)∵∠ADC是△ABD的外角(已知),
∴∠ADC=∠B+∠ =80°
又 ∠B=∠BAD(已知),
∴ ∠ =80°×=40°(等量代换).
(2)在△ABC中,∵∠B+∠ +∠C=180°(三角形的内角和等于180°),
∴ ∠C=180°-∠ -∠ (等式的性质)
=180°-40°-70°=70°
例2、如图所示,在△ABC中,∠A=70°,BO,CO分别平分∠ABC和∠ACB,求∠BOC的度数.
例3、如图,△ABC中,∠A=500,∠ABC的平分线与∠C的外角∠ACE平分线交于D,
求∠D的度数。
三 、 知识巩固应用。(学生独立完成后小组互评教师根据情况点拨)10-15分钟
1.三角形的三个外角中,最多有_______个锐角.
2.已知等腰三角形的一个外角为150°,则它的底角为_____.
3.如图1所示,∠ABC,∠ACB的内角平分线交于点O,∠ABC 的内角平分线与∠ACB的外角平分线交于点D,∠ABC与∠ACB的相邻外角平分线交于点E,且∠A=60°,
则∠BOC=_______,∠D=_____,∠E=________.
4.如图2所示,∠A=50°,∠B=40°,∠C=30°,则∠BDC=________.
5、如图4,则∠A+∠B+∠C+∠D+∠E的度数为 .
6.已知三角形的三个外角的度数比为2:3:4,则它的最大内角的度数为( )
A.90° B.110° C.100° D.120°
7.如图3所示,若∠A=32°,∠B=45°,∠C=38°,则∠DFE等于( )
A.120° B.115° C.110° D.105°
(1) (2) (3) (4)
8、如右图,AC∥DE,BD平分∠ABC交AC于F,∠ABC=70°,∠E=50°,求∠D,∠A的度数.
9、 如图所示,在△ABC中,∠A=α,△ABC的内角平分线或外角平分线交于点P, 且∠P=β,试探求下列各图中α与β的关系,并选择一个加以说明.
I
H
G
E
F
D
B
C
A
5题
l1
l2
l3
3
1
2
P
