多边形小结与复习学案
图片预览
文档简介
多边形小结与复习
学习目的
1、通过学生对本章所学知识的回顾与思考,进一步掌握知识点;
2、经历考点例题解析,使学生进一步提高运用所学知识解决问题的能力。
重点:本章知识点的回顾与整理。
难点:综合运用所学知识解决问题。
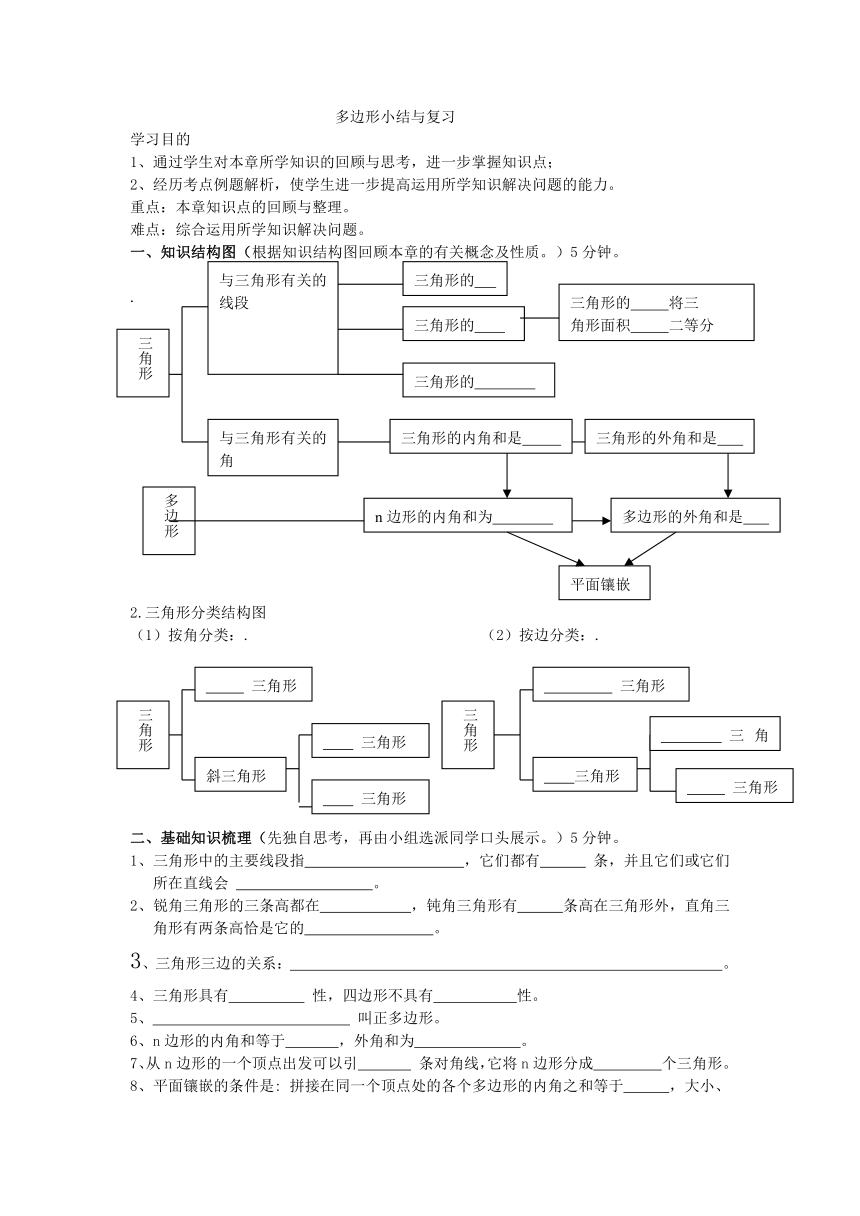
一、知识结构图(根据知识结构图回顾本章的有关概念及性质。)5分钟。
.
2.三角形分类结构图
(1)按角分类:. (2)按边分类:.
二、基础知识梳理(先独自思考,再由小组选派同学口头展示。)5分钟。
1、三角形中的主要线段指 ,它们都有 条,并且它们或它们所在直线会 。
2、锐角三角形的三条高都在 ,钝角三角形有 条高在三角形外,直角三角形有两条高恰是它的 。
3、三角形三边的关系: 。
4、三角形具有 性,四边形不具有 性。
5、 叫正多边形。
6、n边形的内角和等于 ,外角和为 。
7、从n边形的一个顶点出发可以引 条对角线,它将n边形分成 个三角形。
8、平面镶嵌的条件是: 拼接在同一个顶点处的各个多边形的内角之和等于 ,大小、形状相同,能直接进行平面镶嵌的单个多边形有 。
三、典型例题:(先独自做题,在小组比对做法,最后各小组选派一人展示做题过程。)15-20分钟
例1:如图(2),在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63° 求∠DAC的数。
例2:如图,,求的值。
例3、.如图,在△ABC中,∠A:∠ABC:∠ACB=3:4:5,BD、CE分别是边AC、AB上的高,并相交于H,求∠BHC的度数.
例4:已知多边形的一个内角的外角与其它各内角和为600°,求边数及相应的外角的度数。
三 、 知识巩固应用。(学生独立完成后小组互评教师根据情况点拨)10-15分钟
1、若等腰三角形的两边长a、b满足∣a-3∣+(b-8)2=0,则它的周长是 。
2、已知a、b、c是三角形的三边长,化简:|a-b+c|-|a-b-c|=_____________。
3、三角形有两条边的长度分别是5和7,则其周长x的取值范围是___________。
4、一个正多边形的一个外角与相邻的内角的度数比为1:4,则它的内角和是 ,外角和是 ,它共有 条对角线。
5、在下列条件中:①∠A+∠B=∠C, ②∠A∶∠B∶∠C=1∶2∶3, ③∠A=90°-∠B,④∠A=∠B-∠C中,能确定△ABC是直角三角形的条件有 ( )
A、1个 B、2个 C、3个 D、4个
6.下列四种说法正确的个数是( )
①一个三角形的三个内角中至多有一个钝角
②一个三角形的三个内角中至少有2个锐角
③一个三角形的三个内角中至少有一个直角
④一个三角形的三个外角中至少有两个钝角
A.1个 B.2个 C.3个 D.4个
7.等腰三角形两边长分别是5和7,则该三角形周长为( )
A.17 B.19 C17或19 D.无法确定
8:已知的和的平分线BE,CF交于点G。
求证:(1);
(2)
9.如图(1),∠BAC=90°,∠1=∠2,AM⊥BC,AD⊥BE,求证:∠2=∠3=∠4
10、如图BE平分∠ABD、CF平分∠ACD,BE、CF交于G,若∠BDC = 140°,∠BGC = 110°,
求∠A 的度数。
与三角形有关的线段
三角形的
三角形的 将三
角形面积 二等分
三角形的
三角形
三角形的
与三角形有关的角
三角形的外角和是
三角形的内角和是
多边形
多边形的外角和是
n边形的内角和为
平面镶嵌
三角形
三角形
三角形
三角形
三角形
三角形
三角形
三角形
斜三角形
三角形
A
B
C
1
4
3
2
A
B
C
M
N
A
B
C
G
E
F
学习目的
1、通过学生对本章所学知识的回顾与思考,进一步掌握知识点;
2、经历考点例题解析,使学生进一步提高运用所学知识解决问题的能力。
重点:本章知识点的回顾与整理。
难点:综合运用所学知识解决问题。
一、知识结构图(根据知识结构图回顾本章的有关概念及性质。)5分钟。
.
2.三角形分类结构图
(1)按角分类:. (2)按边分类:.
二、基础知识梳理(先独自思考,再由小组选派同学口头展示。)5分钟。
1、三角形中的主要线段指 ,它们都有 条,并且它们或它们所在直线会 。
2、锐角三角形的三条高都在 ,钝角三角形有 条高在三角形外,直角三角形有两条高恰是它的 。
3、三角形三边的关系: 。
4、三角形具有 性,四边形不具有 性。
5、 叫正多边形。
6、n边形的内角和等于 ,外角和为 。
7、从n边形的一个顶点出发可以引 条对角线,它将n边形分成 个三角形。
8、平面镶嵌的条件是: 拼接在同一个顶点处的各个多边形的内角之和等于 ,大小、形状相同,能直接进行平面镶嵌的单个多边形有 。
三、典型例题:(先独自做题,在小组比对做法,最后各小组选派一人展示做题过程。)15-20分钟
例1:如图(2),在△ABC中,D是BC上一点,∠1=∠2,∠3=∠4,∠BAC=63° 求∠DAC的数。
例2:如图,,求的值。
例3、.如图,在△ABC中,∠A:∠ABC:∠ACB=3:4:5,BD、CE分别是边AC、AB上的高,并相交于H,求∠BHC的度数.
例4:已知多边形的一个内角的外角与其它各内角和为600°,求边数及相应的外角的度数。
三 、 知识巩固应用。(学生独立完成后小组互评教师根据情况点拨)10-15分钟
1、若等腰三角形的两边长a、b满足∣a-3∣+(b-8)2=0,则它的周长是 。
2、已知a、b、c是三角形的三边长,化简:|a-b+c|-|a-b-c|=_____________。
3、三角形有两条边的长度分别是5和7,则其周长x的取值范围是___________。
4、一个正多边形的一个外角与相邻的内角的度数比为1:4,则它的内角和是 ,外角和是 ,它共有 条对角线。
5、在下列条件中:①∠A+∠B=∠C, ②∠A∶∠B∶∠C=1∶2∶3, ③∠A=90°-∠B,④∠A=∠B-∠C中,能确定△ABC是直角三角形的条件有 ( )
A、1个 B、2个 C、3个 D、4个
6.下列四种说法正确的个数是( )
①一个三角形的三个内角中至多有一个钝角
②一个三角形的三个内角中至少有2个锐角
③一个三角形的三个内角中至少有一个直角
④一个三角形的三个外角中至少有两个钝角
A.1个 B.2个 C.3个 D.4个
7.等腰三角形两边长分别是5和7,则该三角形周长为( )
A.17 B.19 C17或19 D.无法确定
8:已知的和的平分线BE,CF交于点G。
求证:(1);
(2)
9.如图(1),∠BAC=90°,∠1=∠2,AM⊥BC,AD⊥BE,求证:∠2=∠3=∠4
10、如图BE平分∠ABD、CF平分∠ACD,BE、CF交于G,若∠BDC = 140°,∠BGC = 110°,
求∠A 的度数。
与三角形有关的线段
三角形的
三角形的 将三
角形面积 二等分
三角形的
三角形
三角形的
与三角形有关的角
三角形的外角和是
三角形的内角和是
多边形
多边形的外角和是
n边形的内角和为
平面镶嵌
三角形
三角形
三角形
三角形
三角形
三角形
三角形
三角形
斜三角形
三角形
A
B
C
1
4
3
2
A
B
C
M
N
A
B
C
G
E
F
