2021—2022学年人教版七年级数学上册1.2.2 数轴课件(22张ppt)
文档属性
| 名称 | 2021—2022学年人教版七年级数学上册1.2.2 数轴课件(22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 289.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-07-06 08:34:11 | ||
图片预览



文档简介
第一章 有理数
1.2.2 数轴
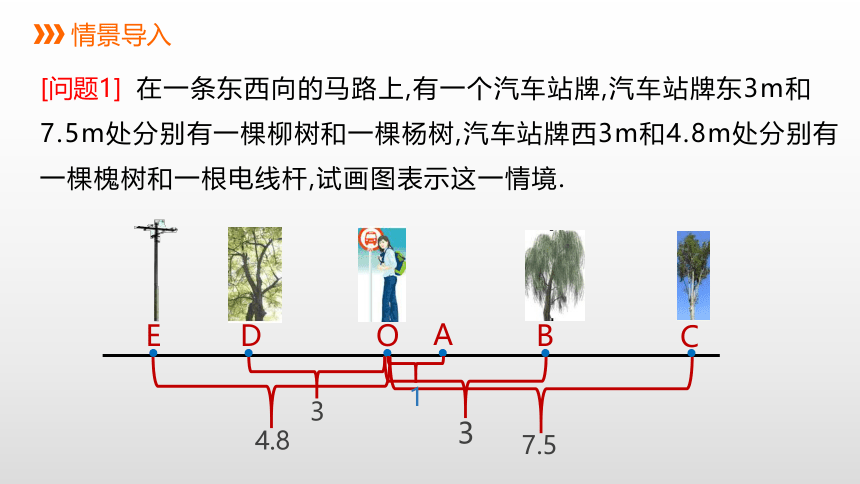
[问题1] 在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
O
A
B
C
D
E
1
3
3
4.8
7.5
情景导入
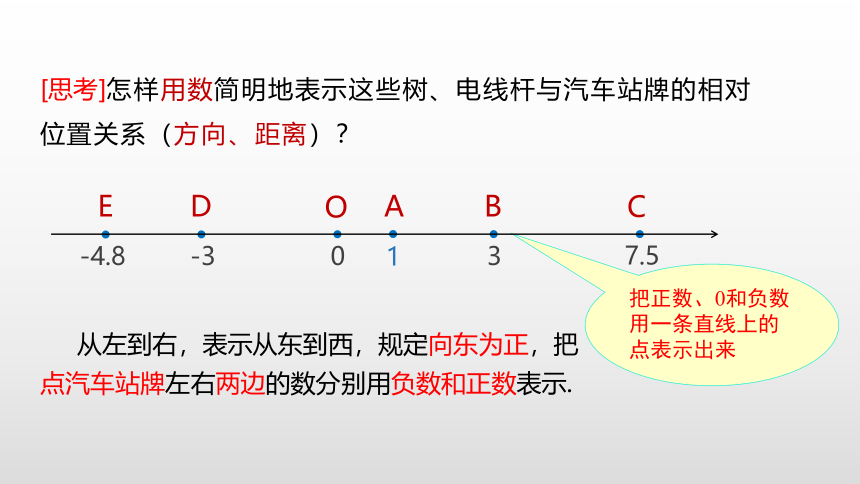
[思考]怎样用数简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
O
A
B
C
D
E
1
3
7.5
-3
-4.8
0
从左到右,表示从东到西,规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
把正数、0和负数用一条直线上的点表示出来
B
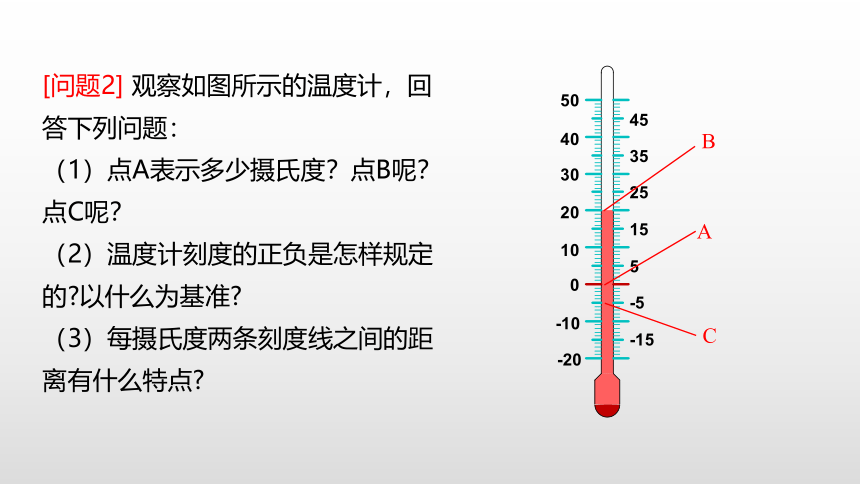
[问题2] 观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的?以什么为基准?
(3)每摄氏度两条刻度线之间的距离有什么特点?
A
C
0
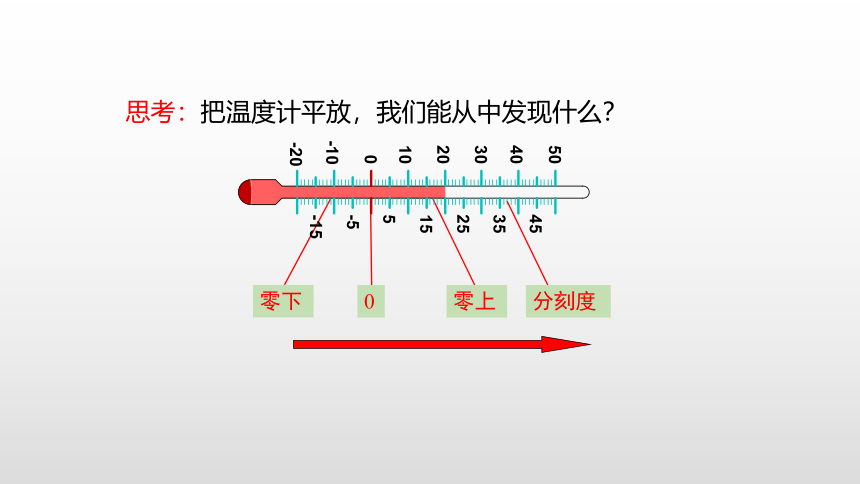
思考:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
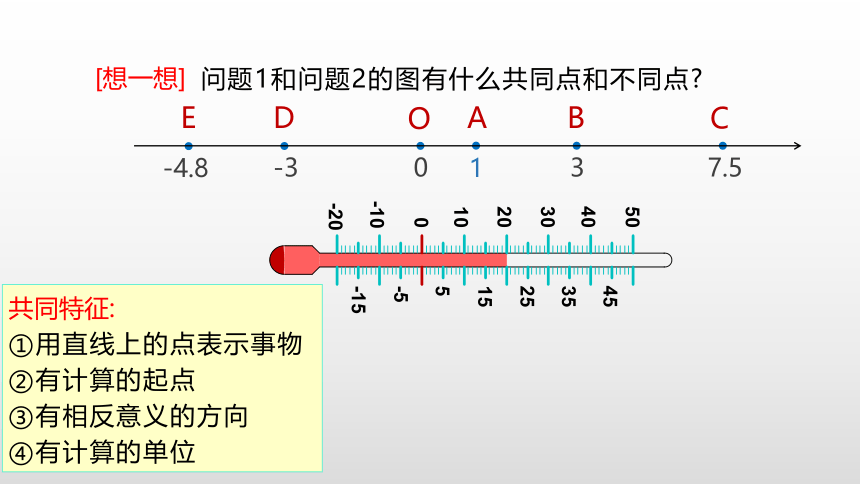
[想一想]
问题1和问题2的图有什么共同点和不同点?
共同特征:
①用直线上的点表示事物
②有计算的起点
③有相反意义的方向
④有计算的单位
O
A
B
C
D
E
1
3
7.5
-3
-4.8
0
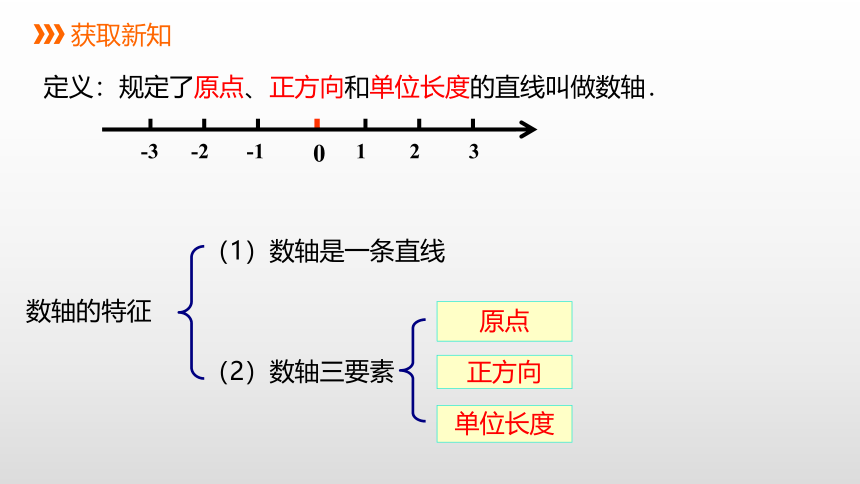
定义:规定了原点、正方向和单位长度的直线叫做数轴.
(1)数轴是一条直线
数轴的特征
(2)数轴三要素
原点
正方向
单位长度
0
-3 -2 -1 1 2 3
获取新知
数轴的画法:
1取:画一条水平直线,定原点(如图),原点表示0.
0
2定:规定从原点向右为正方向,那么相反的方向
(从原点向左)则为负方向.
3统一:选择适当的长度为单位长度.
?
0
0
1
2
3
-1
-2
-3
?
?
4标数:在原点左右两边依次标上对应的刻度数.
例题讲解
例1 下图中,是数轴的是( )
解析:A中没有正方向,B中原点左侧标数顺序错误,
C 中单位长度不统一.
D
备注:识别数轴,要紧扣数轴的定义,围绕数轴的“三要素”进行判断,三者缺一不可.
例2 如图,数轴上的点A,B,C,D分别表示哪个有理数?
分析:考虑两个方面:(1)点的位置:原点表示0,原点右边的点表示正数,原点左边的点表示负数;(2)点到原点的距离是几个单位长度.
(4) D点表示0
(1)A点表示1.5;
(2) B点表示-0.5;
(3)C点表示-2.5;
解:
例3 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
4
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方.
归纳:
数轴的两个最基本的应用:
一是知点读数,
二是知数画点,即:
它是最直观的数形结合体.
归纳:一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
右
a
左
a
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
在数轴上画出表示下列各数的点-1,1,-3,3,a,-a
●
●
-1
1
-3
3
a
-a
随堂演练
1.下列各图中,所画数轴正确的是( )
D
2.下列说法中,错误的是( )
A.在数轴上,原点位置的确定是任意的
B.在数轴上,正方向可以是从原点向右,也可以是从原点向左
C.在数轴上,确定单位长度时可根据需要任意选取
D.数轴是规定了原点、正方向、单位长度的直线
B
3. 如图,分别用数轴上的点A,B,C,D表示数,正确的是( )
A.点D表示-2.5 B.点C表示-1.25
C.点B表示1.5 D.点A表示1.25
C
4.a,b,c 在数轴上的位置如图所示,下列说法正确的是( )
A.a,b,c 都表示正数
B.a,b,c 都表示负数
C.a,b 表示正数,c 表示负数
D.a,b 表示负数,c 表示正数
C
5.点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-6
C.2或-6 D.不同于以上
C
6. 在数轴上表示数6的点在原点_____侧,到原点的距离是_____个单位长度,表示数-8的点在原点的_____侧,到原点的距离是_____个单位长度.表示数6的点到表示数-8的点的距离是______个单位长度.
右
6
左
8
14
7.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是0,-2,1,2.5,-3.
8. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
课堂小结
数轴
定义:
规定了原点、正方向和单位长度的直线叫做数轴
原点、正方向和单位长度.
一是知数画点,二是知点读数.
数轴的“两点应用”:
三要素:
数轴上的点与有理数间的关系:
所有的有理数都可用数轴上的点来表示,但数轴上的点表示的不一定都是有理数.
(数形结合)
1.2.2 数轴
[问题1] 在一条东西向的马路上,有一个汽车站牌,汽车站牌东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站牌西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
O
A
B
C
D
E
1
3
3
4.8
7.5
情景导入
[思考]怎样用数简明地表示这些树、电线杆与汽车站牌的相对位置关系(方向、距离)?
O
A
B
C
D
E
1
3
7.5
-3
-4.8
0
从左到右,表示从东到西,规定向东为正,把点汽车站牌左右两边的数分别用负数和正数表示.
把正数、0和负数用一条直线上的点表示出来
B
[问题2] 观察如图所示的温度计,回答下列问题:
(1)点A表示多少摄氏度?点B呢?点C呢?
(2)温度计刻度的正负是怎样规定的?以什么为基准?
(3)每摄氏度两条刻度线之间的距离有什么特点?
A
C
0
思考:把温度计平放,我们能从中发现什么?
零下
零上
分刻度
[想一想]
问题1和问题2的图有什么共同点和不同点?
共同特征:
①用直线上的点表示事物
②有计算的起点
③有相反意义的方向
④有计算的单位
O
A
B
C
D
E
1
3
7.5
-3
-4.8
0
定义:规定了原点、正方向和单位长度的直线叫做数轴.
(1)数轴是一条直线
数轴的特征
(2)数轴三要素
原点
正方向
单位长度
0
-3 -2 -1 1 2 3
获取新知
数轴的画法:
1取:画一条水平直线,定原点(如图),原点表示0.
0
2定:规定从原点向右为正方向,那么相反的方向
(从原点向左)则为负方向.
3统一:选择适当的长度为单位长度.
?
0
0
1
2
3
-1
-2
-3
?
?
4标数:在原点左右两边依次标上对应的刻度数.
例题讲解
例1 下图中,是数轴的是( )
解析:A中没有正方向,B中原点左侧标数顺序错误,
C 中单位长度不统一.
D
备注:识别数轴,要紧扣数轴的定义,围绕数轴的“三要素”进行判断,三者缺一不可.
例2 如图,数轴上的点A,B,C,D分别表示哪个有理数?
分析:考虑两个方面:(1)点的位置:原点表示0,原点右边的点表示正数,原点左边的点表示负数;(2)点到原点的距离是几个单位长度.
(4) D点表示0
(1)A点表示1.5;
(2) B点表示-0.5;
(3)C点表示-2.5;
解:
例3 在所给数轴上画出表示下列各数的点.
1,-5,-2.5, ,0
-5 -4 -3 -2 -1 0 1 2 3 4 5
4
-5 -4 -3 -2 -1 0 1 2 3 4 5
解:
1
-5
4
●
●
●
●
●
-2.5
0
注意:
①把点标在线上;
②把数标在点的上方.
归纳:
数轴的两个最基本的应用:
一是知点读数,
二是知数画点,即:
它是最直观的数形结合体.
归纳:一般地,设a是一个正数,则数轴上表示数a在原点的____边,与原点的距离是____个单位长度;表示数-a的点在原点的____边,与原点的距离是____个单位长度.
右
a
左
a
-5 -4 -3 -2 -1 0 1 2 3 4 5
●
●
●
●
在数轴上画出表示下列各数的点-1,1,-3,3,a,-a
●
●
-1
1
-3
3
a
-a
随堂演练
1.下列各图中,所画数轴正确的是( )
D
2.下列说法中,错误的是( )
A.在数轴上,原点位置的确定是任意的
B.在数轴上,正方向可以是从原点向右,也可以是从原点向左
C.在数轴上,确定单位长度时可根据需要任意选取
D.数轴是规定了原点、正方向、单位长度的直线
B
3. 如图,分别用数轴上的点A,B,C,D表示数,正确的是( )
A.点D表示-2.5 B.点C表示-1.25
C.点B表示1.5 D.点A表示1.25
C
4.a,b,c 在数轴上的位置如图所示,下列说法正确的是( )
A.a,b,c 都表示正数
B.a,b,c 都表示负数
C.a,b 表示正数,c 表示负数
D.a,b 表示负数,c 表示正数
C
5.点A为数轴上表示-2的动点,当点A沿数轴移动4个单位长度到点B时,点B所表示的数为 ( )
A.2 B.-6
C.2或-6 D.不同于以上
C
6. 在数轴上表示数6的点在原点_____侧,到原点的距离是_____个单位长度,表示数-8的点在原点的_____侧,到原点的距离是_____个单位长度.表示数6的点到表示数-8的点的距离是______个单位长度.
右
6
左
8
14
7.如图,写出数轴上点A,B,C,D,E表示的数.
解:点A,B,C,D,E表示的数分别是0,-2,1,2.5,-3.
8. 画出数轴并表示下列有理数:
1.5,-2.2,-2.5, , ,0.
-3 -2 -1 0 1 2 3 4 5
●
●
1.5
●
-2.2
●
-2.5
●
●
课堂小结
数轴
定义:
规定了原点、正方向和单位长度的直线叫做数轴
原点、正方向和单位长度.
一是知数画点,二是知点读数.
数轴的“两点应用”:
三要素:
数轴上的点与有理数间的关系:
所有的有理数都可用数轴上的点来表示,但数轴上的点表示的不一定都是有理数.
(数形结合)
